Analysis of influencing factors on the method for determining boron concentration and dose through dual prompt gamma detection

Feng Tian · Chang-Ran Geng,2· Xiao-Bin Tang,2· Di-Yun Shu ·Huang-Feng Ye · Silva Bortolussi · Chun-Hui Gong

Abstract A method based on the cross-sectional relationship between 10B(n, α)7Li and 1H(n, γ)2H was proposed to detect and reconstruct the three-dimensional boron concentration/dose distribution in vivo during boron neutron capture therapy (BNCT). Factors such as the neutron energy, fluence rate, and degree of non-uniform distribution of the boron concentration in a voxel may affect the results of this method. A theoretical analysis of the accuracy of the method using a Monte Carlo simulation shows that the determining error is generally less than 1% under different tumor locations and neutron source configurations. When the voxel size is larger than 0.4 cm, the determining error might be higher for a non-uniformly distributed boron concentration in the voxel because of the changes in the neutron energy and fluence rate. In conclusion, the proposed method enables an accurate threedimensional boron determination in vivo during BNCT.

Keywords BNCT·Boron concentration·Prompt gamma·Capture cross section

1 Introduction

Boron neutron capture therapy (BNCT) is a binary radiotherapy based on the10B(n, α)7Li capture reaction,which releases two charged particles (i.e., α and7Li) with high linear energy transfer [1, 2]. The ranges of these particles(α ＜10 and7Li ＜5 μm)are smaller than the cell size (～10 μm), and as a result, the energy is deposited only in the tumor cells where the boron-drug accumulates[3–5]. Therefore, in clinical situations, acquiring the precise distribution of10B is key to predicting the therapeutic effects [6]. However, the blood-boron concentration measurement method used in current clinical trials is limited by its use of universal pharmacokinetics, which cannot accurately describe the three-dimensional distribution of boron drugs in individualized patients during treatment [7, 8].

To address the boron concentration detection problem,a variety of in vivo boron concentration measurement methods have been proposed, and some key technical problems have been studied. Among the in vivo boron concentration measurement methods reported, positron emission tomography (PET) and single-photon emission computed tomography (SPECT) are considered to be applicable clinically.The principle of PET is the detection of annihilation photons emitted from a region of interest(ROI).In clinical studies, patients are injected with tumortargeted drugs labeled with a positron decay nuclide prior to treatment (i.e.,18F-BPA in BNCT). The drugs emit positrons through the decay of radionuclides. The range of positrons is short,and they will quickly annihilate with the surrounding electrons to produce a pair of annihilation photons with the same energy (i.e.,511 keV)and opposite motion directions. Thus, the distribution of annihilation photons is considered as the distribution of tumor-targeted drugs.When the drug distribution is relatively stable after a certain period of injection, a PET scanning device is used to detect and reconstruct the distribution of annihilation photons and thereby obtain the distribution of tumor-targeted drugs in the ROI of the patient.PET scanning can be used to assess whether the patient is suitable for BNCT,and the reconstructed drug distribution can be used in treatment planning.Shimosegawa et al.studied the changes in the concentration of18F-BPA in normal organs of six healthy volunteers and demonstrated that the changes in the10B concentrations of the normal organs are both timedependent and dynamic [9]. These results also illustrate that it is necessary to monitor the boron concentration in normal tissues exposed to irradiation during treatment.Watabe et al. studied a method for estimating the absolute boron concentrations in tissues and tumors using rat xenograft models and determined that an underestimation of the partial volume effect using PET to estimate the boron concentration in the lungs,small intestine,and large intestine will increase the adverse effects[10].Aihara et al.reported the first clinical case of BNCT for head and neck malignancies using18F-BPA PET in Kawasaki Medical School, and the BPA-accumulating capacity of the tumor by18F-BPA PET was confirmed prior to BNCT [11].However, with the current technology, PET imaging can only measure the boron distribution before treatment.Therefore, the therapeutic dose distribution calculated using the boron-drug distribution measured using PET imaging may be different from the dose delivered through BNCT treatment.

As another boron dose monitoring method with significant clinical application potential, the principle of SPECT is to detect the distribution of prompt gamma (PG) rays with an energy of 478 keV, which is different from PET scanning. Approximately 94% of7Li recoil nuclei produced by the boron neutron capture reaction will release 478 keV PG rays.A SPECT scanning system for detecting this PG ray and reconstructing the primary gamma ray(i.e.,prompt gamma rays) source distribution in the ROI of a patient during treatment can be used to estimate the boron dose [12], which is the major component of the total therapeutic dose of BNCT. Theoretically, a method based on SPECT scanning can be used during treatment. To promote the clinical translation of this method,researchers have carried out numerous studies on detectors, instrumentations, and other devices [13]. Semiconductor detectors have attracted significant attention owing to their high stopping power and good energy resolution [14]. Murata et al.focused on the feasibility of using a CdTe detector to detect this PG ray and optimized the design of the detection system to achieve an effective resolution of both the ray and the annihilation photons [13, 15]. Fatemi et al. proposed the use of a CZT detector as a PG detector and carried out a series of experimental feasibility and performance optimization analyses based on the nuclear reactor of the University of Pavia,Italy[12,16].In addition to the research on semiconductor detectors, some scholars have carried out studies on the design and performance of SPECT systems based on scintillator detectors, and many design schemes have been proposed[17–19].In addition to the selection and optimization of detector materials, the optimization of the overall structure of the SPECT system can also improve the detection results because the radiation field of the BNCT environment is composed of neutrons and gamma rays with different energies. Hales et al. proposed a method using BGO as an anti-Compton suppression detector, the results of which indicate that the detection performance was improved[20].Gong et al.used the Monte Carlo method to analyze the influence of boron concentration in tumors on the reconstruction results using the ML–EM algorithm [21]. BNCT-SPECT has a promising prospect for clinical application, but can only estimate the boron dose during treatment, which means it cannot predict the distribution of boron concentration and the total therapeutic dose.

To more comprehensively use the information of PG rays during BNCT, the boron concentration and dose should be measured simultaneously using PG rays with energies of 478 keV and 2.224 MeV, which are generated through the reaction of1H(n,γ)2H.Further research on the reaction mechanisms for this method should be conducted to promote the clinical application of this detection method in the future. In this study, a detection method is proposed to detect and reconstruct the three-dimensional distribution of boron concentration, and a detailed theoretical derivation of this detection method is discussed. The influencing factors(i.e.,neutron energy,anatomical structure,size,and heterogeneity of the voxel) of the method for clinical conditions are demonstrated using the Monte Carlo method.

2 Materials and methods

2.1 Principles for detecting three-dimensional boron concentration and dose in BNCT

In this study, a detection method for the three-dimensional distribution of boron concentration is proposed based on the reaction mechanism of neutrons captured by1H and10B isotopes. The detection method can be expressed through Eq. (1), in which ω10B(i.e., the10B concentration in a voxel of interest) can be calculated as follows:

where M1His the molar mass of the1H isotope (g/mol),M10Bis the molar mass of the10B isotope(g/mol),N0.478is the yield of PG rays with an energy of 478 keV, N2.224is the yield of PG rays with an energy of 2.224 MeV, ω1His the1H isotope concentration in the voxel of interest,ω10Bis the10B isotope concentration in the voxel of interest, and K is the ratio of the cross section of neutrons captured by10B and1H isotopes. In combination with the average energy released in a boron neutron capture reaction (i.e.,Eaveof 2.3388 MeV)and the mass of voxel of interest(m),the boron dose deposited in the voxel of interest(D10B)can be calculated using Eq. (2).

The detailed derivation of the proposed three-dimensional boron concentration detection method used in this study is as follows. As shown in Fig. 1, when an epithermal/thermal neutron beam travels through the tissues of interest, neutrons interact with different isotopes in the tissues.Considering the content of different isotopes in the tissues and the neutron capture cross section, with BNCT,incident neutrons mainly interact with1H and10B isotopes.These reactions emit PG rays with different energies (i.e.,478 keV and 2.224 MeV).

To measure the three-dimensional distribution of the boron concentration,we calculated the boron concentration at the voxel level.For a voxel of interest,the distribution of10B and1H concentrations can be uniformly distributed.Thus, the production rate of different PG rays in the voxel of interest within the neutron irradiation can be described as follows:

where σ1H（E）is the capture cross section of the1H isotope(barn), σ10B（E） is the capture cross section of the10B isotope (barn), φ（E） is the fluence rate of neutrons incident into the voxel, E0is the minimum value of the neutron energy, E1is the maximum energy (MeV), and NAis Avogadro’s constant.

For a given voxel, the concentrations of different elements in a voxel can be considered as constants. Thus, the ratio of PG ray production in a voxel can be described as

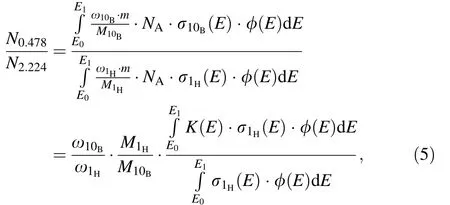
where K(E) is the ratio of the cross section of neutrons captured by the10B and1H isotopes. The cross section of the reaction between neutrons and elements is only related to the energy of the neutron; thus, the physical quantity K(E) can be considered to be related only to the neutron energy.

For a BNCT epithermal/thermal neutron beam,as shown in Fig. 2, the ratio of neutron cross sections that produce the PG rays with 478 keV and 2.224 MeV is almost a constant value over the epithermal/thermal neutron energyrange (i.e., less than 10 keV). In the clinical treatment of BNCT, the neutron beam used is an epithermal/thermal neutron beam. According to the IAEA regulations on neutron beams, it is necessary to ensure that the ratio of epithermal neutrons to fast neutrons in the neutron beam is greater than 20.The influence of fast neutrons was ignored when considering the negligible production of PG rays from fast neutrons.

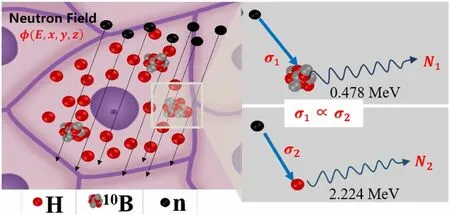
Fig. 1 (Color online)Schematic diagram of PG rays emitted from neutron capture reaction between 10B and 1H isotopes

Fig. 2 (Color online) Relationship of neutron capture cross section between 10B and 1H isotopes. The blue and black lines show the capture cross section of 10B(n,α)7Li and 1H(n,γ)2H,respectively.The red line shows the ratio of 10B and 1H neutron capture reactions of the cross section within the range of a thermal to epithermal neutron[27, 28]

Equation (1) can be obtained by adjusting Eq. (7). In Eq. (1),K,M1H,and M10Bare all constants,and N0.478,and N2.224are the yields of different gamma rays that can be theoretically detected by the three-dimensional PG ray detection system(e.g.,using SPECT or a Compton camera)during BNCT. The last remaining parameter, ω1H, is another important aspect for the feasibility of this boron concentration measurement method.According to previous studies,the hydrogen concentration can be inferred through spectral computed tomography (CT) and material decomposition algorithms [22, 23], allowing the boron concentration to be determined by detecting the PG yield of 478 keV and 2.224 meV PG rays when using the proposed approach. With the development of radiation detection technology [24–26], the boron concentration measurement method has significant potential for clinical applications.

In practical applications, the yield distribution of different PG rays in all voxels should be analyzed to obtain the three-dimensional distribution of the10B concentration in the patient.

2.2 Monte Carlo toolkit and configurations

The Monte Carlo simulation software TOPAS 3.1.2 [29]was used to study the multiparticle transport in this study.TOPAS is a particle therapy research-oriented Monte Carlo platform based on Geant4[30–32].The physical models used in this research include ‘‘G4EMStandardPhysics_option4,’ ‘‘G4HadronPhysicsQGSP_BIC_AllHP,’ ‘G4DecayPhysics,’ ‘‘G4IonBinaryCascadePhysics,’ ‘‘G4HadronElastic PhysicsHP,’ ‘‘G4StoppingPhysics,’and‘‘G4EmExtraPhysics’’[33,34].

The component elements of the tumor and normal tissues set in the simulation in this study were all based on the ICRU report 46 [35]. The neutron energy spectrum simulated in this work was obtained from the Massachusetts Institute of Technology (MIT) reactor neutron source [33, 36]. The number of simulated neutrons used during each simulation was 5 × 108,and the calculations for each data were repeated 10 times to determine the statistics of the results.In the simulations,sensitive detectors and filtering scorers were set to obtain the actual PG ray yield information of each voxel under neutron irradiation. During the simulations, each voxel was set as a sensitive detector to detect the number of PG rays generated in each voxel.In addition,a certain energy divergence is considered when recording the PG rays;that is,the yield of each PG ray recorded is the yield of the PG rays within a certain energy range.For PG rays with an energy of 478 keV,the energy range was set as 477–479 keV,and the energy range was set as 2.223–2.225 MeV for PG rays with an energy of 2.224 MeV.

Fig. 3 (Color online) Geometric structure used to analyze the influencing factors of boron concentration estimation for different influence factors:a The structure used to analyze the influence of the neutron energy on the accuracy of boron concentration measured,b the structure applied to analyze the influence of the tumor depth and surrounding tissue on the accuracy of boron concentration measured,and c the structure used to analyze the influence of the size and heterogeneity of the voxel on the accuracy of boron concentration measured

In this study, three geometric structures were set during the simulations to analyze the different influencing factors on the accuracy of the measured boron concentration, as shown in Fig. 3.When analyzing the influence of different neutron components in the incident neutron beam,the geometric structure set during the simulation is as shown in Fig. 3a. The mass concentration of hydrogen for all tumor tissues set in this simulation was 0.107. The radius of the tumor was 0.5 cm,and the distribution of the1H and10B B isotope concentrations in the tumor voxel was uniform.The boron concentration in the tumor tissue was increased from 10 to 100 ppm at 10 ppm intervals,and only one small tumor tissue was set during each simulation.Figure 3b shows the structure set used to analyze the influence of the tumor depth and surrounding tissue on the accuracy of the measured boron concentration. Two tumor layers were designed at different depths in the tissue. Each tumor layer was composed of 10 tumor tissues with different boron concentrations.The radius of the tumor tissue was set as 0.5 cm,and the depths of the two layers were 3.5 and 5.5 cm from the surface,respectively.At the same depth from top to bottom,the10B concentration in the tumor increased from 10 to 100 ppm at 10 ppm intervals.To consider a heterogeneous situation,a bone tissue with a thickness of 1 cm was placed in front of the first tumor layer and the high boron concentration parts(＞50 ppm)of the second tumor layer.Based on the structure of the tumor depth and bone tissue set, the neutron spectrum and fluence rate will be different for each tumor voxel.Figure 3c shows the structure used to analyze the influence of the size and heterogeneity of the tumor voxel on the accuracy of the measured boron concentration. To investigate the effect,a spherical geometry composed of two regions(i.e.,inner and outer layers)with different10B concentrations was set during the simulations.The density of the voxels with different boron concentrations set during this simulation is considered to be unchanged,i.e., 1.04 g/cm3.By adjusting the size of the inner and outer layers, the average10B concentration of different voxels was 50 ppm,and only one small voxel was set during each simulation.

3 Results and discussion

3.1 Influence of neutron energy on the accuracy of the measured boron concentration

In Eq. (1), it can be seen that N0.478/N2.224should only be related to ω10Band ω1H;however,it can also be affected by other factors.Therefore,this study focuses on analyzing the influence of different factors on N0.478/N2.224, which can also clarify the influence on the accuracy of this method. For epithermal/thermal neutrons, a linear correlation can be observed between N0.478/N2.224and ω10Bwhen ω1Hin a small voxel of interest is known through a theoretical analysis.This finding indicates that K is a fixed value within this energy range.However, the energy range of neutron beams used in clinical BNCT is wide. In highenergy neutrons,K is no longer a fixed value,and the linear correlation may be affected by the high-energy neutrons in the actual BNCT beam. The PG yields corresponding to different neutron components (i.e., thermal neutrons,E ＜1 eV; epithermal neutrons, 1 eV ＜E ＜10 keV; fast neutrons, E ＞10 keV; and high-energy neutrons,E ＞1 MeV) were analyzed to clarify whether K holds a fixed value and determines the effect on the accuracy of the boron concentration prediction.

Figure 4 shows the relationship between N0.478/N2.224and ω10B, where it can be seen that N0.478/N2.224linearly increases with ω10B.Thus,the actual ω10Bcan be calculated using N0.478/N2.224for the actual BNCT irradiation.

Table 1 shows the yields of PG rays corresponding to neutrons with different energies(the values in parentheses are counting errors).Under the simulation setting,the proportion of PG rays generated by fast neutrons was only approximately 0.1% of the total PG yield. The proportion of PG rays generated by high-energy neutrons is less than 0.005%of the total PG yield,and the K corresponding to this energy band is no longer fixed.The results indicate that the PG rays produced by fast neutrons will not affect the three-dimensional boron concentration measurement method proposed in this study,and even within this energy region, K is no longer a fixed value assumed in the theoretical derivation.

Fig. 4 Relation between N0.478/N2.224 and ω10B under uniform 10B distribution

Table 2 shows the relationships between N0.478/N2.224and the boron concentrations from different neutron components. These results indicate that the N0.478/N2.224produced by thermal neutrons and epithermal neutrons are almost equal to the average value produced by all incident neutrons, and the relative deviations between them are almost less than 1%at the same boron concentration in the tumor tissue. Overall, the results indicate that the yield of different PG rays is affected by the outcomes of the thermal and epithermal neutrons. The simulation results prove that although K is not a constant assumed in the theoretical derivation for the actual BNCT neutron beams, the proportion of PG rays and capture cross sections of different elements with high-energy neutrons are sufficiently small.Consequently, these factors did not have a significant negative effect on N0.478/N2.224.

3.2 Influence of tumor depth and surrounding tissue on the accuracy of the measured boron concentration

In the actual BNCT treatment,the neutrons are scattered when neutrons travel through human tissue,and the energy and flux of neutrons reaching the tumor area will become complicated.The yield of different PG rays and the energy deposited in the tumor voxels by complex neutron beams will be significantly different from the results produced bythe ideal neutron beams. Thus, in this section, the influences of the tumor depth and surroundings on the accuracy of the measured boron concentration are analyzed.

Table 1 Proportion of PGs produced by neutrons of different energies

Table 2 N0.478/N2.224 of neutrons with different energies at different 10B concentrations

Based on the geometric structure shown in Fig. 3b, the effect of tissue structure is studied by comparing the PG ratios produced in different tumor layers, the results of which are shown in Fig. 5. The generation of 2.224 MeV PG is only related to the neutron fluence rate and1H concentration; therefore, the neutron fluence rate at the middle position is high, and the two ends are low because of the influence of neutron scattering from the N2.224distribution. By contrast, the N0.478distribution is completely different from the N2.224distribution. With the changes in location and10B concentration of the tumor, N0.478gradually changes. Based on the effect of the neutron fluence rate and10B concentration, N0.478of the tumor with a10B concentration of 80 ppm is the highest. The results in the second layer are similar to those in the first layer;however,the yield of PGs with the same10B concentration is significantly reduced because of the overall decrease in the neutron fluence rate. The comparison results of N0.478/N2.224of the two layers (Fig. 5b) indicate that even if tumors are in different neutron fields,N0.478/N2.224of the two layers are nearly the same, and the deviations are nearly less than 1% when the values of ω10Bare the same.This result shows that the changes in the depth of the tumor and the tissue structure will only affect the yield of the PG rays and not the ratio (N0.478/N2.224) for a voxel with a uniform10B. Therefore, the method of inferring the10B concentration based on the ratio of dual-energy PG yields still applies for tumors at different depths in the human body.

Fig. 5 (Color online) Influence of depth and tissue structure on N0.478/N2.224: a PG yield under different configurations with boron and hydrogen concentration ratios. The red and blue points in the figure represent the PG yield of the first and second tumor layers,respectively. The dot and square points represent N0.478 and N2.224,respectively. b N0.478/N2.224 for different boron and hydrogen concentration ratios and the deviation of different tumor layers. The purple point represents N0.478/N2.224 from the first tumor layer. The purple line represents N0.478/N2.224 from the second tumor layer.The red line represents the relative deviation of these two values

3.3 Influence of the size and heterogeneity of the voxel on the accuracy of the measured boron concentration

In the above study, the distribution of boron concentration in the tumor tissue is even,and thus the influence of boron concentration distribution was ignored. In this case,the average boron concentration of the tumor tissue was equal to the boron concentration of each tumor voxel. In clinical studies, the distribution of boron drugs in patients shows individual differences, and the absorption capacity of boron drugs is also different inside the patient. These factors lead to a non-uniform distribution of boron drugs in the ROI. In this case, the average boron concentration of tumor tissue is not equal to the boron concentration in each tumor voxel, and the yields of different PG rays are different in different tumor voxels. Thus, the influence of boron distribution in a voxel on the accuracy of boron concentration measurements should be clarified.

Figure 6a shows N0.478/N2.224with different voxel sizes and different compositions of the10B concentration. For a uniform distribution of the boron concentration(i.e.,where the boron concentration of the inner and outer layers are both 50 ppm), N0.478/N2.224is nearly unchanged as the voxel size increases. Therefore, the voxel size does not affect N0.478/N2.224when the boron concentration is evenly distributed in the voxels.However,when the distribution of boron concentration in a voxel is uneven, the greater the unevenness of the boron concentration distribution is at the same voxel size,the greater the difference in N0.478/N2.224.For example, when the voxel size is 2.8 cm, the results of 10/90 ppm and 40/60 ppm are 0.3344 and 0.3089,respectively. In addition, in the case of a non-uniform distribution of boron concentration in the voxel, the voxel size will also affect N0.478/N2.224. For example, when the boron concentration in the voxel is composed of 10/90 ppm, N0.478/N2.224is increased from 0.2979 to 0.3344 when the voxel size is increased from 0.4 to 2.8 cm.These changes in N0.478/N2.224indicate that the deviations between the boron concentration measured by this method and the true boron concentration reached more than 10%when the boron distribution in the voxel was non-uniform.Moreover, when the voxel size is large and the degree of non-uniformity of the10B concentration distribution is large (i.e.,the voxel size is 0.8 cm and is composed of 40/60 ppm), the deviation between the actual10B concentration and the average10B concentration obtained using the PG yields of the entire voxel is considerable. Therefore,when using this method in clinical applications,selecting a reasonable voxel size is important to ensuring the accuracy of the boron concentration obtained. Figure 6b shows the deviations of N0.478/N2.224of different voxels with different concentrations, and uniform10B distribution results were selected as a reference. Considering the calculation error,when the deviation is less than 2%,this result is considered to be approximately equal to the reference.When the voxel size is 0.4 cm,the deviations of the results for the four10B concentration compositions are all less than 2%. In some cases, the deviations are greater than 2% when the voxel size increases. For example, when the boron concentration in the voxel is 10/90 ppm,the deviation of the N0.478/N2.224is increased from 0.60 to 3.02% when the voxel size is increased from 0.4 to 0.8 cm. In actual clinical practice,selecting the optimal voxel size based on different treatment plans is the key to obtaining an accurate boron concentration.

Fig. 6 Influence of voxel sizes and boron concentration distribution of tumor voxels on N0.478/N2.224:a N0.478/N2.224 under different boron concentration compositions and voxel sizes and b deviations between N0.478/N2.224 with non-uniform and uniform boron distribution of tumor voxels

4 Conclusion

In conclusion, a method based on the relationship between ω10Band N0.478/N2.224was proposed to detect and reconstruct the actual three-dimensional10B concentration/dose distribution in the ROI during treatment. The accuracy affected by the fast neutrons of the clinical thermal neutron spectrum, voxel size, and heterogeneity distribution of boron concentration in a single voxel was discussed using Monte Carlo simulations. The effect caused by fast neutrons in the clinical neutron spectrum was almost less than 0.1%. The effects of the voxel size and uneven distribution of the boron concentration in a voxel were studied.The results show that the deviations of N0.478/N2.224between different non-uniform10B distributions and a uniform distribution are less than 2%when the voxel size is less than 0.4 cm. Therefore, a voxel size of less than 0.4 cm is suggested in practical applications.

Based on the current technologies of radiation detection and dual-energy CT,the boron concentration measurement method has significant potential for clinical applications.It should be noted that there are many technical challenges to implementing the proposed method in clinical applications.We are currently conducting in-depth research on the clinical implementation of this method and the development of relevant detection devices. Furthermore, the method might not be limited solely to BNCT but might also have the potential to measure the10B concentration and other types of elements in any related field of application.

Authors contributionAll authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by Feng Tian,Chang-Ran Geng,and Xiao-Bin Tang.The first draft of the manuscript was written by Feng Tian and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.