薄壁铜管弯曲成形仿真研究

倪雪辉，江 伟，胡 涛，何正林

（珠海格力电器股份有限公司，广东 珠海 519000）

0 引 言

薄壁铜管因其壁厚薄、换热系数高、成本低而广泛应用于航空航天、军工、汽车、家电等行业。空调行业的换热器通常需要将薄壁铜管进行弯曲加工，以满足空间的限制与减少焊接点的要求。薄壁铜管弯曲成形过程中，经常会出现各种质量问题，包括外侧壁厚减薄严重甚至开裂、内侧受压起皱、横截面畸变严重以及卸载后的回弹等[1,2]。这些质量问题不仅会降低薄壁铜管的强度和耐压能力，而且易导致管内冷媒流速不匀、污质汇集以及涡流产生等，影响空调的正常使用及寿命[3,4]。

国内外学者对薄壁管材弯曲成形的研究主要集中于理论分析、试验研究和数值模拟分析3个方面。巫帅珍等[5]研究了芯棒参数及芯棒伸出量对φ48 mm×2 mm管材的弯曲成形影响；李强等[6]分析了薄壁铜管弯曲中常见缺陷及预防措施，具有一定的实际指导作用。R PEEK[7]为了明确JU G T等[8]预测的起皱波长较试验结果偏长的误差是由小应变假设还是板壳理论所引起的，基于有限元应变理论对圆管纯弯曲过程中的起皱进行研究分析。还有学者[9-11]采用有限元软件建立弯曲模型，研究了芯棒伸出量、芯棒结构以及摩擦条件等对壁厚减薄、横截面畸变、起皱和回弹的影响规律。LI H等[12]研究了薄壁小弯曲半径绕弯工艺中相对弯曲半径与相对壁厚对弯曲成形的影响。

目前，针对管材弯曲成形的研究主要以壁厚＞1 mm的管材为主，而对壁厚＜0.5 mm薄壁铜管的弯曲成形研究较少。为解决薄壁铜管弯曲成形的质量问题，通常会采用芯杆辅助弯曲成形。现通过数值模拟TP2φ7 mm×0.25 mm×0.18 mm（外径×底壁厚×齿高）薄壁铜管的弯曲成形，研究分析芯杆结构与芯杆伸出量对薄壁铜管弯曲成形的影响规律。

1 有限元模型建立

1.1 模型建立

利用ABAQUS软件前处理功能建立各几何部件并进行网格划分，薄壁铜管弯曲成形的3D有限元模型如图1（a）所示。由于在弯曲过程中弯模、夹模、托模及芯杆变形小，基本可忽略，简化成离散刚体结构。考虑铜管壁厚方向的尺寸远小于其他方向的尺寸，可将铜管模型简化为壳体结构，设定单元厚度为0.43 mm，单元类型为S4R。弯管参数设置：弯曲半径R=22 mm，弯管角度θ=180°，芯杆伸出量e如图1（b）所示，即芯杆最大外径处距离弯模中心的水平距离。为解决薄壁铜管弯曲成形的质量问题，通常会采用芯杆辅助弯曲成形，芯杆结构分别选取半圆、椭圆和关节结构芯杆，如图2所示。

图1 模型建立

图2 芯杆结构

1.2 材料选择

研究的铜管材料为TP2（磷二脱氧铜），材料物理性能参数如表1所示。铜管规格为φ7 mm×0.25 mm×0.18 mm，弯曲半径R=22 mm。通过单向拉伸试验，获得铜管的工程应力-应变曲线，试验加载速率为2 mm/min，经转换后得到材料的真实应力-应变曲线，如图3所示。

图3 TP2真实应力-应变曲线

表1 TP2铜管材料物理性能参数

2 结果及分析

2.1 芯杆结构对壁厚减薄率的影响

铜管弯曲后的壁厚减薄率作为评价弯曲质量效果的重要指标，影响铜管的耐压性能以及使用寿命。铜管壁厚越薄，铜管的耐压及使用寿命越短，反之则越长。图4所示为芯杆结构及伸出量对薄壁铜管壁厚减薄率的影响。由图4可知，不同结构的芯杆伸出量对薄壁铜管弯曲成形的影响趋势一致，即随着芯杆伸出量增大，壁厚减薄率均上升，壁厚减薄量越大，但半圆和椭圆芯杆壁厚减薄率相差较小。

图4 芯杆伸出量及结构对薄壁铜管壁厚减薄率的影响

2.2 芯杆结构对成形Mises应力的影响

图5所示为芯杆结构及伸出量对薄壁铜管弯曲成形Mises应力的影响。由图5可知，随着芯杆伸出量增大，弯管成形Mises应力逐渐上升。其中椭圆芯杆与半圆芯杆弯管成形的Mises应力变化趋势基本一致，且数值相差较小，偏差＜5 MPa；而对于关节芯杆，当其伸出量为0～2 mm时，虽然弯管成形的Mises应力随其伸出量增加有上升趋势，但变化并不明显；当其伸出量为2～4 mm时，成形时的Mises应力随其伸出量增加而明显增大。芯杆伸出量e=4 mm时，3种规格芯杆的Mises应力相差较小，且均处于极限值附近，此时薄壁铜管易出现开裂、起皱等质量问题。

图5 芯杆结构及伸出量对薄壁铜管Mises应力的影响

2.3 芯杆结构对铜管横截面畸变的影响

管材弯曲件横截面畸变通常导致横截面面积减小，增加管内流体流动的阻力，影响管件的功能效果，因此有必要对薄壁铜管弯曲后横截面畸变进行控制。弯曲成形后铜管横截面近似椭圆，故以弯扁率（椭圆长轴与短轴之比）作为畸变评价指标。

图6所示为芯杆结构及伸出量对薄壁铜管弯曲成形弯扁率的影响。由图6可知，随着芯杆伸出量增大，半圆芯杆和椭圆芯杆所对应的弯扁率逐渐降低，即可有效保持薄壁铜管弯曲处的圆度；关节芯杆则与之相反，随着芯杆伸出量增大，铜管的弯扁率逐渐增加。图7所示为不同芯杆结构及伸出量弯管横截面畸变，反映芯杆结构及伸出位置对弯管后铜管横截面的畸变程度。

图6 芯杆伸出量及结构对薄壁铜管弯扁率的影响

图7 芯杆结构及伸出量对薄壁铜管横截面畸变程度的影响

2.4 有限元模型验证

仿真模拟结果的准确与否须以试验加以检验。由于试验中无法直接测得铜管弯曲成形过程中的应力应变，以铜管厚度作为衡量仿真结果的标准，即将壁厚最大值、最小值或减薄率作为评价对比指标。利用线切割技术将弯曲后的薄壁铜管沿图8（a）所示平面切割，测量该截面处的壁厚，结果如图8（b）所示，基于测得的壁厚最大值及最小值，与图8（c）所示仿真结果进行对比。经计算，试验测量结果与仿真结果之间的误差小于5%，验证了仿真结果的可靠性，可有效用于薄壁铜管弯曲成形的模拟与生产指导。

图8 弯曲成形样件

3 分析

铜管在弯曲过程中，通常以管材中性层位置作为分界，弯曲处内侧和外侧都有不同的应力应变状态，如图9所示。取铜管弯曲外侧（A）和内侧（B）2个具有代表性的点进行应力应变分析[13]，切向θ、径向r以及周向D应力应变分析如图9（b）所示。薄壁管材弯曲成形过程由3个阶段构成：①弹性变形阶段，该变形阶段表现为管材外侧受拉、内侧受压的应力状态，应力与应变呈线性变化关系；②弹塑性变形阶段，随着应变的增加，当应力与应变不再呈线性变化关系时，开始进入弹塑性变形阶段；③纯塑性变形阶段，图9（b）所示为完全进入塑性变形时的应力应变状态，此时变形区最外侧和最内侧所受的切向应力最大，且内外侧壁厚落差也逐渐增大。切向应变εθ是管材弯曲成形中的主应变之一，也是导致铜管外侧壁厚减薄、开裂与内侧壁厚增厚、起皱的主要原因。

铜管弯曲成形中，材料流动主要表现为轴向和周向的塑性流动，材料的轴向流动方向如图9（c）所示，铜管外侧材料因受拉而使壁厚减薄，而内侧材料因受压向圆弧中心流动而使铜管壁厚增加。材料的周向流动如图9（d）所示，铜管内侧材料沿着圆管向外侧流动，具有抑制内壁增厚和外壁减薄的趋势。

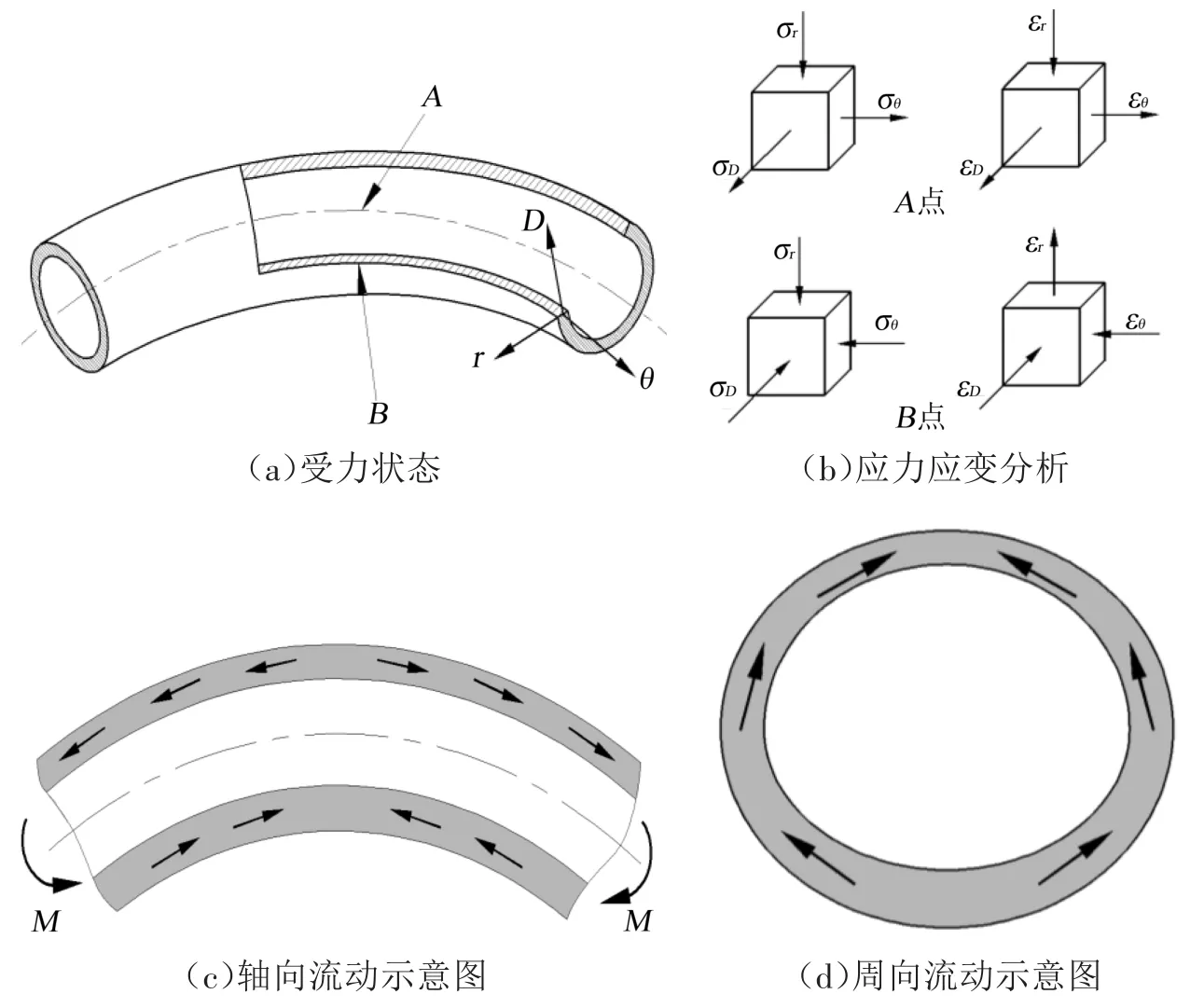
图9 管材弯曲分析

为改善薄壁铜管横截面畸变程度，一般通过增加芯杆来辅助弯曲成形，但会导致壁厚减薄率相应增加。若芯杆伸出量过小，则芯头不能充分支撑铜管内部，易导致弯扁或截面畸变，由于弯扁率改善区间有限，随着芯杆伸出量的增加，支撑区域前移可有效改善弯扁率；若芯杆伸出量过大，则导致铜管弯曲内侧与弯模之间的间隙增大，易出现内侧起皱、外侧开裂等质量问题。

4 结束语

（1）仿真结果与试验结果误差小于5%，即采用显示算法可指导薄壁铜管弯曲成形。

（2）在一定范围内，铜管的壁厚减薄率、Mises应力均随芯杆伸出量增加而增大；综合考虑壁厚减薄率、Mises应力以及横截面畸变程度，芯杆伸出量e应控制在1.5～2 mm。

（3）伸出量e=2 mm时，半圆芯杆有利于改善壁厚减薄，椭圆芯杆有利于改善横截面畸变，关节芯杆各方面指标最佳。