ARIMA 乘积季节模型在惠州市手足口病疫情预测中的应用
谢中勇,陈伟明,廖康荣 (广东省惠州市第一妇幼保健院,广东惠州 516000)
2008 年始手足口病(HFMD)疫情在安徽省阜阳市发生,随后在全国各地均有流行,HFMD 已成为当今社会关注的重要公共卫生问题[1],2008 年5 月起HFMD 纳入丙类传染病[2],给我国儿童带来严重的健康威胁和疾病负担。近年来,越来越多的数学模型在传染病早期预测中得到广泛应用,当前传染病预警模型种类较多,包括有传染病动力学模型、神经网络模型、空间统计学等[3-5],不同的模型有其各自的特点及适用范围。1970 年提出了非平稳自回归移动平均求和模型[6](ARIMA)及建模使用方法,广泛应用于公共卫生领域。本研究基于ARIMA 乘积季节模型对2019年1-6 月惠州市手足口病发病率的趋势进行预测。
1 资料和方法
1.1 一般资料
本研究中所有手足口病数据来自惠州市“传染病报告信息管理系统”子系统,经漏报调查等回顾性调查进行质量控制。人口数据来自《惠州市统计年鉴》。
1.2 模型基本原理
据惠州市2008 年1 月至2018 年12 月手足口病月发病数建立时间序列。手足口病月发病数时间序列属于季节性时间序列,故采用乘积季节模型,即ARIMA(p,d,q)×(P,D,Q)s。其中d 为平稳化过程中差分的阶数,p、q 为自回归和移动平均阶数。P、Q 为季节性自回归和移动平均阶数,D 为季节差分阶数,s为季节周期。
1.3 统计学处理
利用SPSS 25.0 统计软件,通过ARIMA 模型分析方法建立预测模型,将2019 年1-6 月实际发病率与模型测算出的预测发病率与相对误差(相对误差=|实际值-预测值|/实际值)进行比较,评价模型预测效果。
2 结果
2.1 序列平稳化、平稳性检验

图1 惠州市手足口病发病率序列图
绘制2008 年1 月-2018 年12 月惠州市手足口病发病率时间序列图(图1),该序列为非平稳序列,需利用季节差分,使序列平稳。由图1 可见惠州市手足口病发病有明显的季节性,惠州市手足口病全年各月均有病例报告,以12 个月为流行周期。每个流行周期出现2 个流行高峰,大高峰出现在5~7 月,小高峰出现在9~11 月。差分后的时间序列自相关和偏自相关函数未见截尾和拖尾现象(图2、3),差分后的时间序列接近平稳,可以构建ARIMA 乘积季节模型。
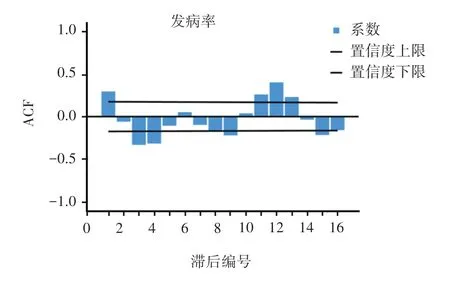
图2 原始序列经过一次季节差分后自相关系数图

图3 原始序列经过一次季节差分后偏相关系数图
2.2 模型识别、模型参数估计和检验
根据差分后序列自相关函数图和偏自相关函数图,构建合适的ARIMA 模型。本研究利用非线性最小二乘法估计模型参数,模型的拟合优度采用标准化的贝叶斯准则比较,标准化BIC 值最小,并结合残差是否为白噪声、BIC 值的大小、Ljung-Box Q 统计量P>0.05的模型为最优。为模型初步识别和定阶,需确定p、d、q 和P、D、Q 的值。惠州市手足口病月发病率序列通过一阶季节性差分后,自相关系数自二阶后截尾,偏自相关系数截尾,表明该模型应为AR (2) 过程,且d=0,D=1,p=2,q=0,s=12。根据序列季节化特征和平稳化处理过程,d=0,D=1。根据自相关函数图和偏自相关函数图,p=1,q=1。文献报道[7],季节模型P、Q 值较难判断,但参数P、Q 很少超过2 阶,模型形式初步判别为ARIMA(p,0,q)X(P,1,Q),通过比较模型参数、结合模型的拟合优度、残差以及系数间的相关性进行估计,采用Ljung-Box 方法检验残差白噪声,非白噪声模型排除(表1)。经试验,模型ARIMA(2,0,1) (1,1,0)12标准化BIC 值(6.087) 最小,平稳R2=0.743,Ljung-Box=20.195,P=0.124,残差序列的自相关系数及偏相关系数均在95% 置信区间内,该模型被选为最优模型(图4)。

表1 备选ARIMA 模型残差检验及拟合优度比较

图4 ARIMA(2,0,1) (1,1,0)12模型自相关和偏相关系数图
2.3 评价模型预测效果
比较惠州市2019 年1-6 月的实际发病率与预测发病率相对误差,验证模型预测效果(图5,表2)。本研究针对惠州市手足口病预测数据与实际发病情况区间估计一致,在预测值95%CI 内。惠州市2019 年1-6 月手足口病月发病率预测最小相对误差为9.95%,手足口病发病的预测值同实际值之间存在一定差异,但包括发病高峰在内的基本趋势拟合良好,提示预测结果可信。

图5 2008-2018 年手足口病月发病率预测图

表2 ARIMA 模型实际值与预测值比较(/10 万)
3 讨论
动态监测是评估HFMD 疫情变化的有效方法,并可提供科学依据以制定精准的防控政策[8]。惠州市各级医疗卫生部门加强疫情监测、学校晨检等多措并举的措施,做到防治HFMD 的关口前移[9]。目前,及时有效地预测、预警HFMD 发病趋势,是预防控制工作的重点和难点[10]。
本研究运用ARIMA 模型对HFMD 进行短期预测,把相关因素的效应关联到时间变量中,克服了相关因素的相互影响[11],适用于HFMD 具有明显的季节特征变化的预测[12]。本研究利用2008 年1 月至2018 年12 月11 年共132 月惠州市HFMD 月发病率资料作为时间序列,通过拟合预测及效果评估等步骤,建立了ARIMA(2,0,1)(1,1,0)12为最优模型,从区间预测看,本预测模型相对误差最低为6 月份的9.95%,HFMD 发病的预测值同实际值之间存在一定差异,但2019 年1-6 月HFMD 实际发病率基本在预测模型的95% CI 内,与武汉、宁波、江门市等地[13-15]应用ARIMA 模型预测当地HFMD 发病率的结果相似,其中以江门市预测模型的平均相对误差较小,可能与各地人口、社会因素等不同有关[16]。因此,ARIMA 模型能够在短期内、实际发病趋势无较大波动时,对惠州市HFMD 发病率进行了较好的拟合预测,为HFMD 疫情变化提供科学依据[17]。在HFMD 实际防控工作中,HFMD 疫情受气候因素、人口流动等诸多因素影响[18],因此有学者根据当地的情况,采取组合模型对HFMD 发病率进行预测[19],减少混杂因素干扰,提高预测准确率,使其具有更高的指导价值。

