基于广义随机有色Petri网的测试性建模方法
翟禹尧, 史贤俊, 韩露, 吕佳朋
(海军航空大学 岸防兵学院, 山东 烟台 264001)
0 引言
测试模型的优劣决定了测试性设计水平的高低,当前应用最广泛的模型当属多信号模型,信息流模型紧随其后[1-2]。信息流模型主要考虑故障与测试之间的关系,忽视系统功能,致使其描述能力有限,阻碍了提升的空间。多信号模型解决了上述模型的一些不足,简化了故障模式,采用信号描述故障和测试之间关系有效降低了建模难度。陈春良等[3]建立了某坦克火控系统的多信号模型,并对其进行测试性分析,提高了火控系统的测试性水平。孔令宽等[4]采用多信号模型对卫星电源进行了测试性建模与分析,提出了基于多信号模型的实时故障诊断技术。孙智等[5]采用分层多信号流图对飞机空调系统进行了故障诊断,取得了不错的效果。张晔等[6]对雷达机内测试(BIT)的测试能力进行了评估,并建立了多信号模型。
多信号模型虽然解决了信息流模型的不足,但其仍有一些弊端。例如:系统故障与测试之间的关系仅用0和1描述,其内在联系不能完整地表达出来,并且面向机电、控制系统等复杂系统不再适用;忽略大量有用信息,如漏检和虚警的影响、延时性以及故障间的逻辑关系,导致模型不够完备,所得测试性分析结果不够全面准确。不少学者针对上述不足做了以下研究,杨鹏[7]、陈希祥等[8]对模型进行了改进研究,添加了一定的不确定性知识。陈希祥等[9]还提出基于本体的描述模型。徐星光等[10]将测试性结构模型和测试性贝叶斯网络模型相结合,融合了先验知识和实际试验结果,利用不确定信息提高了装备测试性水平。
综合看来,不少专家对当前模型进行了一定改进及调整,使模型具备了表达不确定信息等功能,但这些方法没有从根本上解决测试性建模问题,如测试时延、故障间的逻辑关系以及故障严酷度等信息。Petri网描述系统状态的同时还表现其行为,由于自身特点使其在很多领域广泛应用[11]。故障Petri网在可靠性、安全性方面应用较多[12],本文不做研究。随机Petri网是Petri网的进一步扩展[13],可以描述系统状态及其动态变化。王瑶[14]对可靠性、安全性、维修性、测试性工作开展了深入研究,将系统正常状态、故障状态、功能失效状态引入随机Petri网中,起到了良好的效果。文献[15]采用广义随机有色Petri网(CGSPN)建立系统层次测试性模型,对系统层次划分进行了详细阐述,添加了编码方式和严酷度信息,增强了模型的可视化并丰富了模型的内容,但是没有考虑测试和故障之间的不确定性问题。
本文在文献[15]基础上对故障间的复杂性进行分析,完善测试性模型的构建;利用专家评分的先验知识与小样本测试数据的后验知识对模型中的不确定信息进行处理,引入三角模糊数算法获取专家知识,计算关于故障检测率的先验条件概率分布以历史测试数据作为后验条件,由贝叶斯公式更新故障检测率的概率分布,解决了数据容量小的问题。
1 基于CGSPN的测试性模型
1.1 Petri网基本理论
定义1满足下列条件的4元组PN=(P,T;F,M0)构成Petri网,其中:P表示库所,T表示变迁,F为弧权函数,M0为初始标识。
1)N为基本网。
2)M为系统状态标识,M:P→Z,Z为自然数。
3)变迁发生规则:
①变迁t∈T,若∀P∈t*,M(P)≥1,则t可被触发,记作M[t>,其中t*为变迁t的后置集,M(P)为库所标识。
②M′为触发后标识,则
记作M[t>M′. 其中p为某种故障模式的故障检测率;*t为变迁t的前置集;标识M可以用1个非负整数的m维向量表示,向量元素满足M(i)=M(Pi),Pi为一个库所,i=1,2,…,m.
可达性(见定义2)是Petri网建模过程中分析的重要方式。
定义2Petri网PN=(P,T;F,M0),系统标识∃M1,M2,…,Mi,…,Mk,使得∀1≤i≤k,对于任意变迁∃ti∈T:[ti>Mi+1,则称变迁序列σ=t1,t2,…,ti,…,tk在M1下是使能的,Mk+1从M1是可达的,记作M1[σ>Mk+1标识。
广义随机Petri网(GSPN)由一个7元组构成[15-16],记为GSPN=(P,T;F,M0,I,O,λ),其中:I和O为输入矩阵、输出矩阵;λ表示变迁速率或概率。
表1所示为GSPN元素的基本含义以及其符号表示方法。
1.2 故障模式在Petri网表达方式
1.2.1 故障模式编码、严酷度等级划分
在实际工作中,严酷度较高的故障一旦发生,会带来严重后果,在模型中根据颜色可以清楚地看到每个库所(故障模式)的严酷度,密切关注严酷度较高的故障并设置相应的测试,会为后续的故障诊断提供方便,有效保护装备系统。根据国家军用标准GJB/Z 1391—2006 故障模式影响及危害性分析指南[17],故障模式的严酷度分为:灾难级、严重级、轻度级和轻微级4类[18],分别对应红色(R)、橙色(O)、黄色(Y)和蓝色(B)。应当说明的是,除了上述4类故障模式外,本文还定义了一种功能失效状态,对于具有n种功能模式的元件,其功能失效状态亦有n种。不同于上述故障模式,功能失效状态称为失效级,用白色(W)表示。
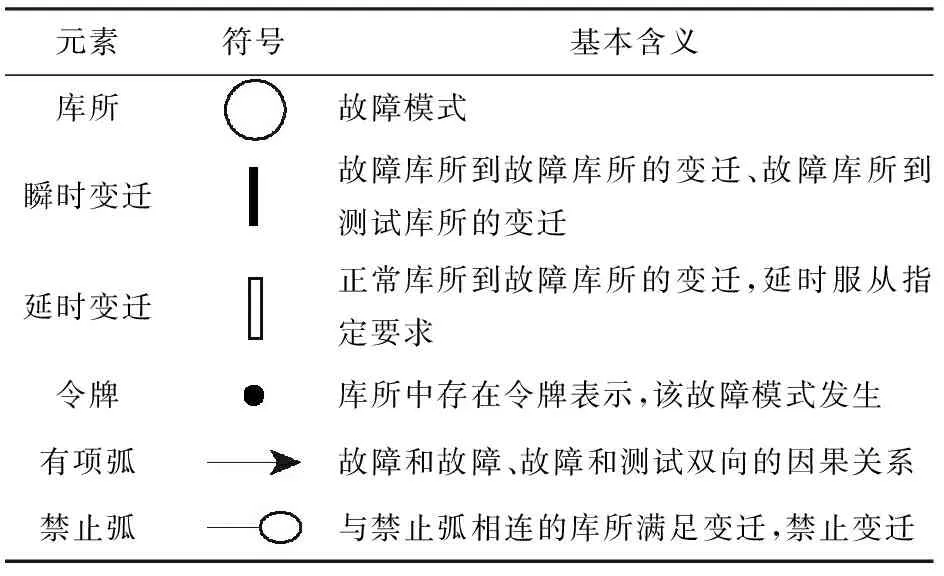
表1 GSPN模型的图形化表示Tab.1 Graphical representation of GSPN
本文定义的颜色属性用于区别模型中各故障模式的严酷度,为后续测试优化选择的研究提供方案。值得注意的是该颜色属性与传统有色Petri网的概念不同[19],模型结构不会因为有色属性的消失而改变。
对复杂系统建模,需要考虑某个故障可能存在多个故障模式,为了降低建模难度并提高系统测试性,本文采用以下编码方案[15]:编码方案:XXX-XXX-XXX-OO.x. 其中,XXX代表系统、现场可更换单元(LRU)和车间可更换单元(SRU)等,可以继续划分到元器件;OO.x中OO为不同严酷度的颜色,x∈n为元件的故障模式种类。
1.2.2 故障传播分析
系统故障传播具有横向性、纵向性、复杂性、时间性以及逻辑复杂性等。故障会逐级传递,从底层元件传递至系统层[14]。对装备进行分层处理就完成了故障传播的横向性、纵向性处理;考虑到导弹长期贮存、一次性使用的特点,其故障模式特点与飞机等常规武器装备不同,时间性特点并不明显。考虑到篇幅,逻辑复杂性在本文暂不作研究,只对故障模式的复杂性展开论述。
一般来说,导弹故障模式存在相容和相斥两种形式。相容模式在模型中表达如下:1个库所表示一种故障模式,令牌流入某个库所,则代表该故障发生。根据1.2.1节所述为库所编号,并根据故障模式、影响和危害性分析(FMECA)中故障严酷度等级为库所赋予颜色。此外库所与故障模式共用1个编号,以确保库所在模型中的唯一性。图1(a)所示为相容模式的简单实例,第2个库所编号为001-001-001-O.1,表示系统的元件编号为001-001-001,其严酷度等级为严重级。

图1 故障模式在Petri网中的表现形式Fig.1 Failure modes in Petri net
对于相斥模式,其表示方法可分为以下两个步骤:
1)表达方式与相容模式相同,首先赋予库所颜色属性以及编码方案。
2)与相容模式不同之处在于使用了禁止弧。假设系统存在故障模式A和B,若A与B相斥,则在系统中找出B库所的前置变迁集合T,在A库所与变迁ti(ti∈T)之间添加禁止弧,表示A发生后B禁止发生。若B发生后A禁止发生,则在库所B以及A库所的前置变迁间添加禁止弧即可。图1(b)所示为3个故障模式相斥时的Petri网。
本文在模型中设置正常状态库所,并为延时变迁赋予相应的随机分布,目的是使CGSPN具有表达元件由正常到故障这一随机过程。实际工作中,用绿色表示正常状态。若某个元件具有K种故障模式,则需要在模型中设置K个正常状态库所,使得正常库所与故障模式的库所一一对应。图2所示为元件4种故障模式的简单实例。从图2中可以看出:变迁点火变化前,令牌存在于001-001-001.G.x(x=1,2,3,4)中呈现绿色,系统正常;满足点火条件后,库所001-001-001.R.1、001-001-001.O.1、001-001-001.Y.1、001-001-001.B.1存在令牌,系统出现故障。

图2 变迁在CGSPN中的表达形式Fig.2 Expression of transition in CGSPN
1.3 构建思路
在测试性模型中,某个测试点与测试项没有明确对应关系,本文对其不做研究。假设测试点与测试项一一对应,故障检测率、故障隔离率的计算与该假设无关。以该假设为前提,将测试项信息添加到CGSPN模型中:
1)测试项库所的建立:为每个测试项建立1个库所。
2)故障与测试之间的关系用有向流和瞬时变迁表示。定义测试库所的颜色为黑色(B),目的是与模型中的其他库所区分。
其基本构建思路如下:
1)建立库所,元件对应的库所包括故障模式、功能失效和正常状态3种状态;子系统级别以上包括故障和正常2种状态。
2)建立延时变迁,设置在正常库所和故障库所之间,完成系统中元件由正常状态到故障发生的描述。
3)建立两类瞬时变迁,第1类设置在故障库所与故障库所之间;第2类设置在故障库所与测试库所之间。
4)为起始库所设置令牌。
1.4 基于CGSPN的测试性模型
CGSPN定义为一个9元组Σ=(P,T;F,K,M0,α,β,η,Fs),其中:
1)P={PG,PS,PF,Pt}为库所集合,PG、PS、PF分别对应正常、故障和功能失效的库所集合,Pt为测试库所集合;
2)T={Td,Ti,Tf},Td为正常库所到故障库所间的延时变迁集合,Ti为故障库所到故障库所间的瞬时变迁集合,Tf为故障库所到测试库所间的瞬时变迁集合;
3)F为弧权函数;
4)K:P映射为{0,1},是Σ中库所容量函数;
5)M0与前文含义相同;
6)α为一个映射,表示颜色属性,α:PG映射为{G},PS映射为{R,O,Y,B},PF映射为{W},Pt映射为{B};
7)β为一个映射,β:Td为延时变迁服从的分布类型及函数,表明Σ存在随机性,如Weibull(α,β)、Exp(λ)等;
8)η为一个映射,η:Ti,Tf为瞬时变迁;
9)Fs为已触发的变迁序列集合,系统未运行时Fs=∅;Fs可以避免系统陷入循环,并记录令牌的传播路径[19],对于模型分析至关重要。
需要注意的是,本文主要针对测试性模型开展研究,在建模中只需要考虑故障和测试之间的关系,得到相关性矩阵即可,元件由正常向故障衍化的随机过程不做考虑,故在仿真前将PG类库所及后置延时变迁删除。
1.5 可达性算法
故障- 测试相关性矩阵(DM)简称D矩阵,D的获取是测试性设计至关重要的一步。根据定义2对故障传播过程进行可达性分析,获得D矩阵的算法,简称可达性算法,其基本原理如下:
首先将系统库所的初始状态记为0,然后根据仿真需求设置令牌于某个初始库所中,满足变迁条件后该令牌会进行流动,最后将其经过的库所做出相应的标记如下:将令牌到达的故障库所或测试库所标记为1,并将该库所作为起始库所,让令牌继续传播。其具体步骤在文献[15]种给出具体描述,本文不做赘述。
2 不确定信息处理方法
在实际工程中,测试与故障存在不确定性问题,为了描述故障与测试之间不确定性问题,用三角模糊函数确定先验专家知识,与实验获得的测试数据作相结合,完成故障- 测试不确定相关性矩阵的确定。
2.1 贝塔分布
贝塔分布是[0,1]区间上的连续概率分布,其与二项分布共轭先验,利用该性质可以将专家的先验信息和实际的测试数据相结合。
通常认为故障检测率的计算模型服从二项分布,则故障检测率p的先验分布可用Beta(a,b)表示,p的概率密度函数记为f(p;a,b)。Beta(a,b)为标准化函数,其概率密度积分等于1,a、b为β分布的组成参数。
p(t|f)为故障f由测试t检测的先验概率,则有
p(t|f)=f(p;a,b),
(1)
Beta(a,b)分布表达式为
(2)
其期望和方差为
(3)
(4)
根据(3)式和(4)式可得
(5)
2.2 基于三角模糊数的专家知识处理方法
在装备测试性设计初期,相关测试性信息不够充分,一些信息需要依赖专家知识进行确定。本文采用三角模糊函数对专家知识进行处理,以确保专家知识的权威性和可靠性。l位专家对p的评分结果为1(s1,q1,u1;θ1),2(s2,q2,u2;θ2),…,j(sj,qj,uj;θj),…,l(sl,ql,ul;θl)。其中,sj(j=1,2,…,l)为p的下限,qj为p的可能最大值,uj为p的上限,θj为第j位专家的评分权重。令ωj为归一化处理后的权重,
(6)
专家的平均评分模糊数为
(7)
式中:s为p的下限期望;q为p的可能最大值的期望;u为p的上限期望。
基于上述处理后,p的先验期望和方差为
(8)
(9)
式中:n=1,2,….
可通过(8)式、(9)式和(10)式计算β分布的组成参数a、b:
(10)
式中:V(p)为分布方差。
最后根据先验信息得到Dpt|f,
(11)
式中:元素ptl|fk为故障由测试检测到的概率,tl|fk表示故障fk由测试tl检测,k为总的故障个数。
2.3 融合测试数据的后验分布确定方法
结合成败型数据(x,N),根据贝叶斯理论及(1)式,得到p的后验分布为
pb(t|f)=f(p;a+x,b+N-x),
(12)
式中:N表示测试次数;x表示通过测试的次数。推理过程可参考文献[19],则经实际测试数据修正后的D矩阵为
(13)
矩阵中的元素可由(12)式计算得到,含义为故障可由测试检测的后验概率。根据Dpbt|f开展测试性评价工作,用FDRg表示fg的故障率,用Ag表示测试检测故障的事件,假设各个测试检测同一故障的事件是相互独立的,则有
FDRg=pb(t1+t2+…+tl|fg)=
pb[(t1|fg)+(t2|fg)+…+(tl|fg)]=
pb(A1+A2+…+Ag),
(14)
式中:g=1,2,…,k,从而有
(15)
3 实例分析
本文选择文献[10]的例子进行建模分析,导弹测试性指标一般要求故障检测率FDR≥0.95,故障隔离率FIR≥0.92. 图3所示为某型飞航导弹系统结构框图,系统分为系统级、分系统级和设备器件3个层级。表2所示为故障模式及其编码,包含8个故障模式,故障率单位为10-6. 测试有6个,分别为电气状态字检查t1、电子控制单元(ECU)状态字检查t2、继电器动作遥测指示t3、发动机IO输出线路电压测量t4、发动机点火信号的输出频率采集t5、发动机转速表状态指示t6. 文献[10]没有提到故障模式相斥,经查阅资料和相关FMECA,确定发动机点火继电器故障与发动机点火装置故障相斥。故障之间关系有利于测试的设置,有效减少测试个数。例如两种关键故障需要同时设置2个测试进行检测,但是两种故障模式相斥,不会同时发生,因此只需设置1个测试即可,从而为多故障诊断奠定了基础。

图3 某型飞航导弹的系统结构框图Fig.3 Block diagram of a winged missile system
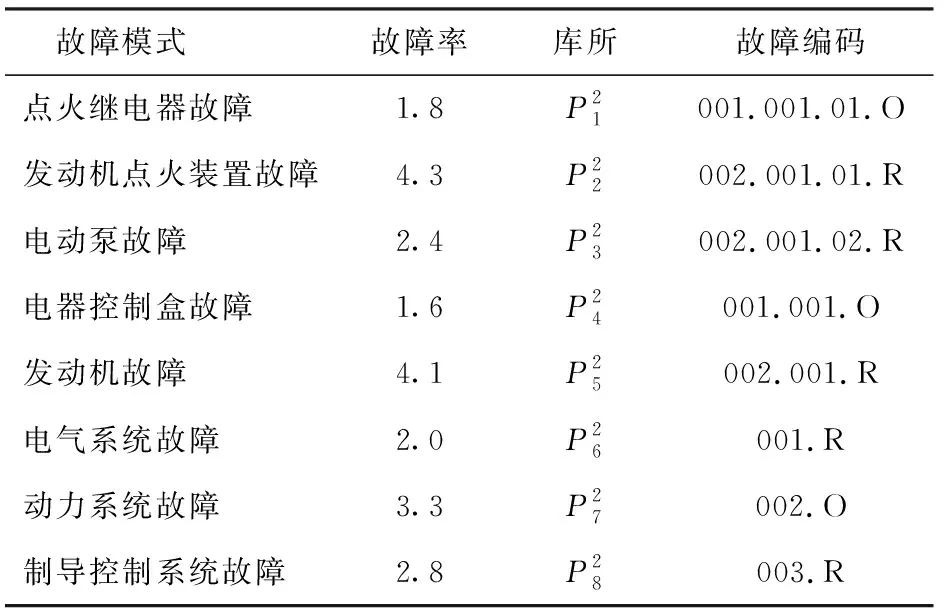
表2 故障模式及其编码Tab.2 Failure modes and codes
考虑到故障传播纵向性,高层次系统的故障一般源于低层次子系统故障,而文献[10]中实例模型的传播方向相反,与实际不符。采用本文所提模型重新建立该系统的测试性模型,如图4所示。图4中,Pt表示导弹由其子系统的故障模式而引起的功能失效。由图4可见,相比于文献[10]以及多信号模型,本文模型不仅可以描述故障传播过程,还可以描述故障的严酷度以及故障模式的复杂性等属性。

图4 某飞航导弹分层CGSPN模型Fig.4 Layered CGSPN model of a winged missile
根据图4得到故障相关性矩阵如表3所示,选定总体、电气和控制专业领域专家评分,采用三角模糊数算法统计评分结果,得出各个故障模式可被检测的先验概率为f(p;a,b),融合先验信息的概率矩阵为Dpt|f:

限于篇幅,飞行试验后积累的历史测试数据不一一列举,根据表3以及(12)式将测试历史数据与先验条件概率融合,得到融合后验信息矩阵Dpbt|f:

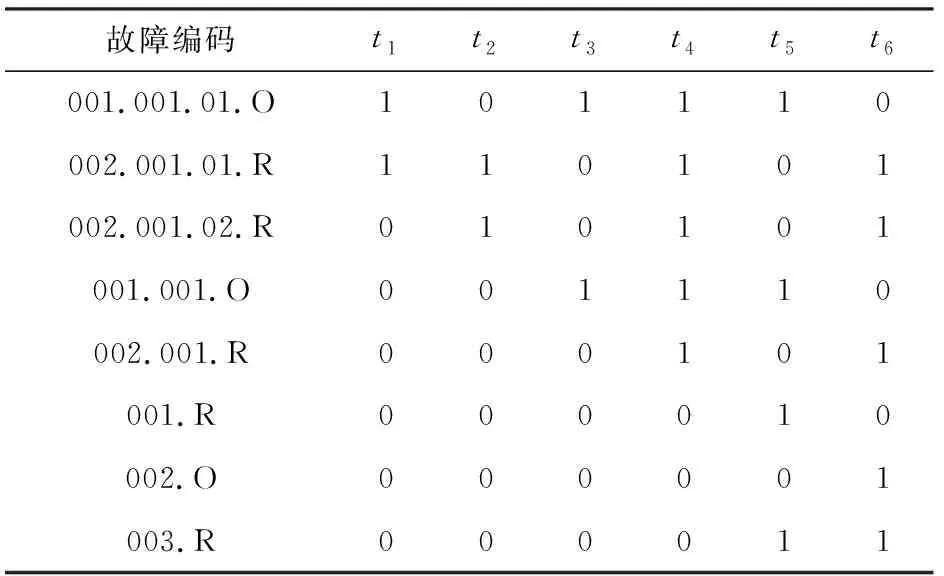
表3 相关性矩阵Tab.3 Correlation matrix
选取矩阵元素期望,得到用于测试性评价的D矩阵:
在MATLAB软件中编程,以FDR3为例进行计算,以说明(14)式的计算方式,矩阵中各个测试对相同故障检测的事件相互独立,根据p(AB)=p(A)p(B)和(14)式,有
FDRi=pb(t1+t2+…+tl|fi)
FDR3=pb[(t2|f3)+(t4|f3)+…+(t6|f3)]=
pb(A2+A4+A6)=pb(A2)+pb(A4)+pb(A6)-
pb(A2A4)-pb(A2A6)-pb(A4A6)+pb(A2A4A6)=
pb(A2)+pb(A4)+pb(A6)-pb(A2)pb(A4)-
pb(A2)pb(A6)-pb(A4)pb(A6)+
pb(A2)pb(A4)pb(A6)=
0.75+0.71+0.81-0.75×0.71-0.71×
0.81-0.75×0.81+0.71×0.81×0.75=0.986.
经过计算,得到每种故障模式的故障检测率分别为FDR1=0.995,FDR2=0.992,FDR3=0.986,FDR4=0.996,FDR5=0.972,FDR6=0.912,FDR7=0.924,FDR8=0.970故障模式的故障率,并根据(15)式可以得到装备总体的故障检测率FDR=0.968. 矩阵中没有相同行,故障检测即可隔离FIR=1,满足指标要求。
4 结论
本文针对传统测试性建模定性描述故障和测试之间关系的问题,提出了一种新的测试性建模方法。首先在模型中引入严酷度等级,完成故障模式的分类、编码和着色;然后对系统、子系统以及元件在模型中的表达进行了详细论述,考虑装备的复杂性,将系统进行层次划分,完成模型的构建。得到以下主要结论:
1)相比于文献[10]以及多信号模型,CGSPN在完成测试性建模的基础上聚焦于故障模式的严酷度、故障模式的复杂关系以及故障发生的随机过程。在模型中根据颜色可以清楚地看到每个库所的严酷度,密切关注严酷度较高的故障并设置相应的测试,可以有效避免危害性故障的发生,也可以为后续的测试优化选择做好铺垫。
2) 引入三角模糊数算法获取专家知识,将专家数据作为先验信息,与实验获得的测试数据作为后验数据相结合,用来解决数据量少和不可靠问题。
3)通过实例分析,得到96.8%的故障检测率和100%的故障隔离率,满足系统测试行指标要求,验证了模型的有效性。
4)虚警率的研究和确定将是后续的研究方向。

