1/n 冷储备系统可靠性评估通用模型*

李志强，曾 翔，顾钧元，徐廷学

（1.解放军91388 部队，广东 湛江 524024；2.海军航空大学，山东 烟台 264001）

0 引言

复杂系统中每个元件都具有很高的可靠度，如果想进一步提高单个元件的可靠度，难度大、成本高、成效不明显。因此，提高复杂系统可靠性水平的普遍方式就是采用冗余设计［1-2］。对于难以停机维修的复杂系统，如处于极端环境条件下的装置、必须长期处于运行状态的设备、停机将带来巨大经济损失的系统，采用冗余设计是保证系统高可靠性最有效、最直接的方法。在并联系统中，冗余结构设计包括3 种方式：热储备方式，当工作元件工作时，储备元件也工作；温储备方式，当工作元件工作时，储备元件处于休眠状态；冷储备方式，当工作元件工作时，储备元件不工作。其中，已有诸多学者针对热储备系统进行了深入研究［3-6］。因此，冗余设计的研究重点逐渐从热储备系统延伸到温储备系统和冷储备系统领域［7-11］。

相比于热储备系统，冷储备系统中备份元件具有接近于0 的失效率，系统具有最高的可靠度。温储备系统作为热储备系统和冷储备系统的折中选择，比热储备系统消耗较少的电源、元件具有较低的失效率，比冷储备系统备份元件模式转换更迅速。李振等［12］提出了将温储备系统和冷储备系统近似于热储备系统的可靠性归一计算方法。在温储备系统中，储备件在储备期间失效率相对工作状态时低，但是，其失效率是确实存在的。在冷储备系统中，储备件失效率为0，应用该近似算法进行可靠性评估时因参数设置的不同而出现不同程度的误差。此外，近似算法中假设元件的故障失效时间服从指数分布，对于不同分布类型的失效函数无法应用文献［12］中的方法进行确定。鉴于复杂系统中，元件寿命主要服从指数分布模型、正态分布模型和威布尔分布模型，本文建立的冷储备系统可靠性评估通用模型以这3 种分布类型为对象展开研究。

1 模型构建

如图1 所示，n 元件冷储备系统的动态故障树模型，其中，元件A1为初始元件，元件A2～An为冷储备元件。假设所有元件统计独立，所有储备元件从左到右依次使用，当所有元件失效时，冷储备系统失效。当元件A1在T1时刻失效时，元件A2代替A1继续工作运行，当元件A2在T1+T2时刻失效时，元件A3代替A2继续运行，依此类推。假设元件更换瞬间完成，时间段T1，T2，…服从独立同分布。因此，在冷储备系统中作出如下假设：

1）冷储备系统中所有元件统计独立；

2）任务期间冷储备系统不可维修；

3）冷储备系统元件之间没有共因失效，即储备元件在使用之前不会发生失效；

4）系统故障检测完全可靠；

5）冷储备系统中储备元件启动失效的概率为0，基于此，冷储备元件相对于热储备元件和温储备元件更为可靠；

6）冷储备系统及其元件均为二状态，即工作运行状态与故障失效状态。

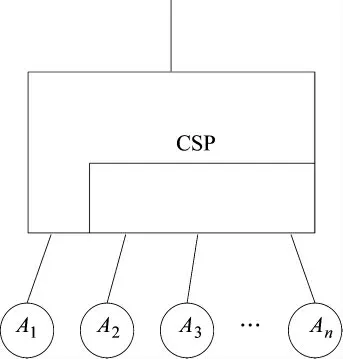
图1 具有n 个元件的冷储备系统

用Sn表示冷储备系统中第n 个元件失效时的时间，则有：

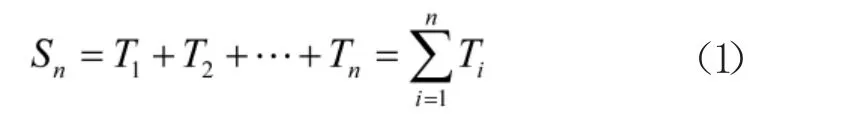
根据大数定理［13］，有：

式中，μ 表示冷储备系统中每个元件的平均失效时间。

根据中心极限定理，Sn的近似正态分布为：

式中，σ 表示Ti的标准差。

则冷储备系统的不可靠度近似为：

式中，Φ（·）表示标准正态分布N（0，1）的分布函数。

2 不同分布模型的可靠性评估方法

2.1 指数分布模型

基于近似评估模型式（4），故障失效时间服从指数分布的冷储备系统不可靠度表示为：

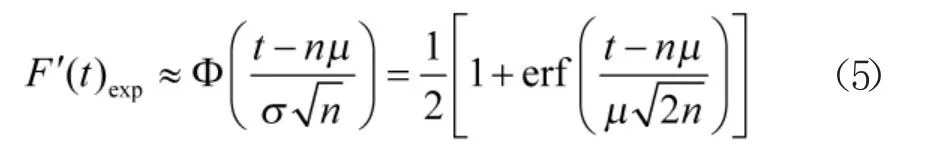
式中，μ 为冷储备系统中元件的平均失效时间，σ 为Ti的标准差，当系统中元件的故障失效时间服从指数分布时，μ=σ，erf（·）为误差函数，有：

作为对比，建立图1 所示冷储备系统的Markov状态转移过程，如下页图2 所示。

图2 冷储备系统的Markov 模型

由于冷储备系统处于各个状态的概率值之和等于1，即：

应用拉氏变换与反拉氏变换即可求解Markov模型，确定冷储备系统的不可靠度函数［14-15］：

2.2 正态分布模型

应用近似评估模型式（4），确定元件故障失效时间服从正态分布时冷储备系统的不可靠度函数：

依此类推，即可确定由n 个元件组成的冷储备系统不可靠度函数：

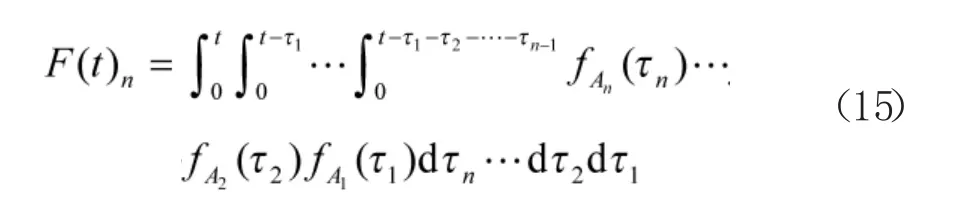
由于每个元件的故障失效时间服从相同正态分布，冷储备系统的不可靠度表示为：

2.3 威布尔分布模型

威布尔分布的概率密度函数表示为：

式中，η 为尺度参数，β 为形状参数。

当β＜1 时，元件的失效率随时间增加而逐渐降低，这一趋势在元件的早期失效期比较明显；当β=1时，元件的失效率为常数，此时的威布尔分布函数转化为指数分布函数；当β＞1 时，元件的失效率随时间逐渐增加，这一阶段的元件出现不同程度的退化或者老化。

威布尔分布函数的标准差为：

代入式（19），威布尔分布函数的标准差进一步表示为：

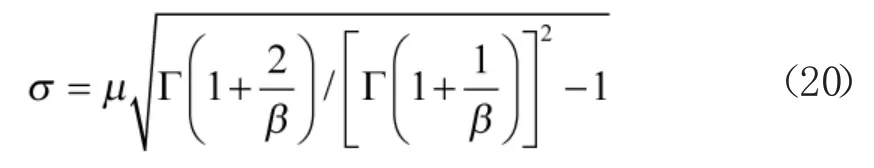
因此，当元件服从威布尔分布时，冷储备系统的近似不可靠度函数表示为：

当β=2 时，冷储备系统的不可靠度函数为：

鉴于Markov 模型难以对威布尔分布函数建模，应用积分法确定冷储备系统的不可靠度：

3 可靠性评估通用模型仿真分析

3.1 指数分布模型

假设冷储备系统中元件的平均失效时间为μ=1 000、配 置 的 元 件 数 分 别 为n=2、n=5、n=10 和n=40，应用式（5）、式（11）确定冷储备系统的近似不可靠度函数与精确不可靠度函数，曲线如图3 所示。作为定量分析，选取冷储备系统不同时间点的不可靠度值，并计算精确值与近似值之间的误差，如表1 所示。从图3 和表1 可以看出，近似值与精确值之间误差不大，式（5）可以作为冷储备不可靠度的近似评估方法。随着系统储备元件的增加，冷储备系统精确值与近似值之间的误差逐渐降低，即近似评估方法越精确。

3.2 正态分布模型

假设冷储备系统中元件的平均失效时间为μ=1 000、标准差σ=200、配置的元件数分别为n=2 和n=3，应用式（13）、式（16）确定冷储备系统的近似不可靠度函数与精确不可靠度函数，对比结果如下页图4 所示。冷储备系统中不同时间点的不可靠度值以及精确值与近似值之间的误差，如表2 所示。从图4 和表2 可以看出，近似值与精确值几乎重合，式（13）可以作为冷储备系统不可靠度的近似评估方法。计算机系统运行环境为Intel i7-7700H Q 处理器、8.00 G 内存、256 G 固态硬盘，当元件为n=2 时，式（16）的整个仿真过程运行时间约为4 s，当元件为n=3 时，式（16）的整个仿真过程运行时间约为82 s。随着元件数量的增加，多重积分的计算越复杂、计算量越大，因此，当元件数量较多时可以考虑用近似评估方法式（13）进行代替。

图3 指数分布模型不可靠度曲线

表1 指数分布函数仿真结果对比

图4 正态分布模型不可靠度曲线

表2 正态分布函数仿真结果对比

3.3 威布尔分布模型

假设冷储备系统中元件的平均失效时间为μ=1 000、威布尔模型的形状参数β=2、配置的元件数分别为n=2 和n=3，应用式（21）、式（23）确定冷储备系统的近似不可靠度函数与精确不可靠度函数，对比结果如图5 所示。冷储备系统不同时间点的不可靠度值以及精确值与近似值之间的误差，如表3 所示。从图5 和表3 可以看出，近似值与精确值之间误差不大，式（21）可以作为冷储备系统不可靠度的近似评估方法。当元件为n=2 时，式（23）的整个仿真过程运行时间约为63 s，当元件为n=3 时，式（23）的整个仿真过程运行时间约为902 s。随着元件数量的增加，多重积分的计算越复杂、计算量越大，因此，当元件数量较多时可以考虑用近似评估方法式（21）进行代替。

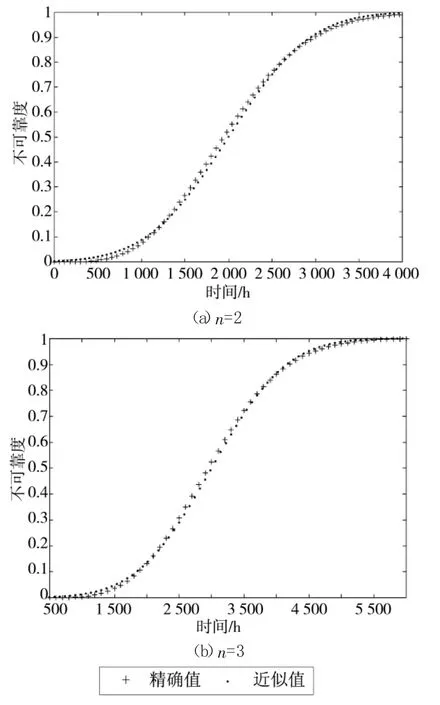
图5 威布尔分布模型不可靠度曲线

表3 正态分布函数仿真结果对比

4 结论

针对冷储备系统近似于热储备系统时，可靠性评估结果受参数设置影响大、且元件寿命必须服从指数分布的问题，从冷储备系统工作原理出发进行模型构建，提出了通用评估方法：

1）对于元件寿命服从指数分布的冷储备系统，当储备元件增加时，其可靠性评估的精确值与近似值之间的误差逐渐降低；

2）对于元件寿命服从正态分布和指数分布的冷储备系统，可靠性近似评估方法相对于原始方法计算简单，便于在工程上推广应用；

3）由于当前只针对1/n 冷储备系统进行分析研究，因此，下一步将在此基础上深入分析k/n 冷储备系统的可靠性评估通用方法。