基于功率谱密度矩心的轴承性能退化特征研究

吴孟祝，李郝林

（200093 上海市 上海理工大学 机械工程学院）

0 引言

滚动轴承作为机械传动系统中最常用的机械零件之一，对于机械系统有着不可替代的作用，其退化的状态在一定程度上直接关系到机械系统的正常运行[1]，对于滚动轴承性能退化的研究十分有必要。此外，通过对其性能退化的研究以及对早期故障的检测，也可以实现对滚动轴承的寿命预测，减少由于轴承出现故障而引发的车间停工事件，为工厂车间的工作人员对轴承制定维修维保计划提供非常重要的参考价值，提高车间的工作效率并降低维修成本。

在分析数据的过程中可以了解到，滚动轴承产生的信号是十分典型的非平稳随机信号，该信号具有较大的随机性和不确定性，如果能够寻找到一个非常合适的量化指标，能够十分清晰地表征轴承的退化趋势，或者在性能退化较为轻微时，能够准确无误地给工作人员提供预警指示，那么该指标对于提升机械系统的可靠性、降低故障发生的频率、完善系统的维保方案都具有重要的意义。

对于一般工业轴承而言，有多种较为成熟的技术，由于传感器性能的不断提高，可以实现对油脂或油量、温度、声音、振动等多种信号的采集。现如今，各研究工作者对轴承性能退化的研究主要基于采集的振动信号，通过傅里叶变换、小波变换、熵值分析等方法将信号分别置于时域、频域、时频域进行分析，实现对滚动轴承性能退化的研究。然而，轴承退化所引起的脉冲以及产生的振动信号具有强非线性和非静态调质特性[2-4]；同时，由于各轴承的工况不尽相同，采集的信号也会混有不同类型的噪声和干扰[5]。退化特征一般无法直接表现出均匀分布或者有规律的特性，这对特征提取和退化识别的研究造就了一定的瓶颈。

针对上述非线性问题，不同学者采用了相应的研究方法。Kaiming He[5]，Huang N E[6]等人提出了经验模态分解（Empirical ModeDecomposition），适用于分析非线性和非平稳信号。尽管该方法在故障检测和故障诊断等领域已经得到了应用，但是缺少较为明确的理论基础，也存在抗干扰能力差、虚假模态、端点效应和易产生模态混叠等缺陷[7]。为了解决模态混叠问题，Wu Z H[8]等人提出了EEMD（Ensemble EMD），有效抑制了模态混叠现象。小波变换通过有限长的会衰减的小波基对信号进行时间频率的局部化分析，将信号逐级分解，实现多尺度细化，可以改善时域分析的不足，但是其计算成本巨大且冗余系数有限。

简言之，在对滚动轴承性能退化的研究中，要选择一种直观且置信值高的特征作为退化指标，要实现这一目的，也要选择一种较为合适的信号分析方法。

结合上述问题以及对实验数据的观察和分析，本文采用EEMD 的方法，对所采集的信号进行降噪和重构以去除干扰，方便后续特征的提取。由于滚动轴承工作过程中产生的振动数据受到多个独立随机变量的影响，可近似地认为该退化指标服从高斯分布。通过中心极限定理可得，该随机变量服从正态分布，且该分布的位置由信号的均值决定，其形状和尺度由方差决定。

研究表明，滚动轴承振动信号在时域的各项指标不能很好地体现滚动轴承的变化，然而在频域的研究表明，频谱可以较好地反映各不同频率谐波能量对信号幅值的影响。通过帕斯瓦定理也可以得知，时域和频域之间功率守恒。因而，本文通过研究信号的功率，采用不同时刻功率密度谱矩心变化值作为滚动轴承的退化指标，通过高斯拟合实现轴承的退化预警，为轴承所在系统提供相应的维修参考。

本文中指标的建立流程如下：

（1）对振动信号进行EMD，EEMD 分析，滤波降噪。获得其本征模函数以后筛除高频噪声分量，对信号进行重构，在保留信号本身特征的同时，确保时频的分辨率；

（2）对振动信号进行傅里叶变换，计算该信号对应的功率谱密度，并计算其对应的功率谱密度矩心值；

（3）对滚动轴承的功率谱密度矩心进行高斯模型拟合，所选择的高斯函数个数为n=4，计算模型的各个参数，确定该模型的表达式。

对应的振动信号的处理流程图如图1 所示。

图1 特征指标建立流程图Fig.1 Flow Chart to build the feature

1 经验模态分解法（EMD）

EMD 是基于信号的局部特征时间尺度，通过数据的局部特征时间尺度来获得本征波动模式，经过预设的筛选机制将信号进行分解，最后得到一组关于信号本身固有的本征模函数（Intrinsic Mode Function,IMF），分解得到的IMF 为原始信号的分量，且每一个IMF 与其他的IMF 正交。

EMD 分解过程如下：

（1）找出原始数据序列x(t)的极大值点，并用三次样条插值函数拟合形成原数据上包络线；同样，提取数据序列的极小值点，并用三次样条插值函数拟合形成数据的下包络线，计算上下包络的平均值并记为m1。

（2）将原始数据x(t)减去包络平均后的新数据m1得到新的数据序列h1：

（3）如果h1满足IMF 的条件，那么h1就是求得的第一个IMF 分量，否则，将h1作为原始信号重复步骤（1）到步骤（2），知道i 次迭代后差值为h1,i(t)满足IMF 条件，记为

i 次迭代的终止条件是S∈（0.2，0.3）。

式中：T——总的采样点数。

（4）用采集的原始数据x(t)减去c1(t)得到第一阶段的余量r1（t）

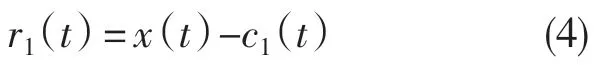
（5）将余量r1(t)作为原始数据进行步骤（1）到步骤（4），提取所有的IMF 分量，rn(t)为最后的余项

通过以上分解方式可得信号

2 集合经验模态分解（EEMD）

采用EMD 方法对滚动轴承的振动信号进行分析，会出现严重的端点效应和模态混叠现象，这些弊端严重影响到后续性能退化研究等工作的准确性。为了解决上述缺陷，集合经验模态分解（EEMD）方法应运而生。它通过添加白噪声辅助数据进行分析，可以有效抑制EMD 分析中的模态混叠现象，也可以辅助研究者在分析信号时，对于阈值和基函数的选择等问题。

其分解步骤如下：

（1）向采集得到的原始数据x(t)中加入m组白噪声，可以得到一组新生成的数据集xi(t)(i=1,……，m)；

（2）将新生成的数据集逐个进行EMD 分解，每个数据集可得到n 个IMF 分量cij(t)(j=1,……，n)以及余量Ri(t)。将m 个信号进行分解以后可得到信号xi(t)(i=1,……，m)的n 个IMF 分量，即

（3）对分解得到的m 组IMF 分量求均值可得{C1,C2,…,Cn}，对该m 组IMF 分量的余量求均值可得R。原始数据x(t)经过EEMD 后得到的n 个IMF 分量可表示为

其对应的算法流程如图2 所示。

图2 算法流程图Fig.2 Algorithm flow chart

3 退化指标建立

3.1 功率谱密度函数

滚动轴承所产生的振动轴承数据是由于不同随机变量相互作用得到，其对应幅值的最终叠加结果可以近似估计为高斯分布，其均值逐步向零逼近。当正态分布的均值趋近于零时，唯一能表征随机信号的就只有均方值以及方差。通过对均方值和方差的量纲分析发现，均方值代表了能量概念，方差则代表了平均功率。由帕瓦斯定理可得，信号对应的能量无论是在时域还是在频域总是满足守恒定律的。

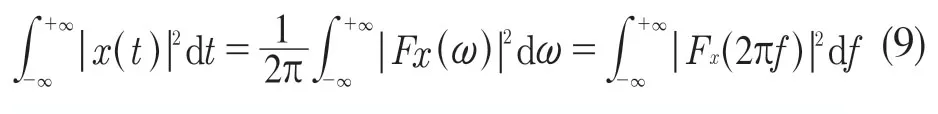
式中：Fx（ω）——x（t）的傅里叶变换。

通过查阅文献可知，在对信号的分析过程中，通过傅里叶变换以后得到信号幅值在各基频谐波的信号分量可以用于筛选主要的信号特征，也可以用于滤波降噪等，即傅里叶变换正是通过各谐波所占能量的角度来观察不同频率谐波在原始信号中的参与度。然而，仅通过对各谐波分量的能量分析，不能较为直观地反应该信号的单位频带所占能量随频率变化的情况。为了解决上述问题，傅里叶提出了功率谱密度函数，即

3.2 功率谱矩心

通过所采集的信号对正常的滚动轴承和发生退化的轴承数据做功率谱密度分析以后发现，随着轴承的性能不断发生退化，其频谱中幅值普遍上升。与此同时，信号中的高频分量逐渐增加，且该高频频带对应占比的功率也在不断上升。即当性能未发生退化时，信号的主要频率集中在低频阶段，随着性能的不断退化，其对应的功率谱的重心开始出现偏移。

因此，本文提出将振动信号功率谱的矩心作为一个特征，用于表征滚动轴承性能的退化过程。此功率谱矩心的计算公式如下：

式中：A（n）——频率幅值；f（n）——对应频率。

3.3 模型拟合

在数据分析的过程中，由于实际采集的值多是离散的有限数据，为了进一步分析数据的变化趋势，可以对离散数据进行拟合。由于滚动轴承的振动信号是由于多个独立随机变量共同作用而得，可以近似认为其退化指标服从高斯分布。因此，基于高斯模型拟合对于时间和退化指标的分析更具有优势[9]，本文对其进行高斯模型拟合。高斯模型拟合是以高斯函数为基础进行拟合，在研究过程中应用广泛。

高斯模型是由多个高斯函数线性叠加而得，其表达式如下：

式中：αi，βi，γi——第i 个高斯函数的峰值增益、第i 个高斯函数峰值对应位置、第i 个高斯函数对应的峰值宽度；n——高斯函数的总个数。高斯拟合模型对应的函数个数n 一般会在数据拟合之前选定好，一般情况下，是由数据本身的峰值个数决定。由于滚动轴承退化失效时通常会出现波动，因此一般将n 值设定在3～5 之间，剩下的3 个参数可由非线性最小二乘法计算得出。

对于损失函数loss(x)，

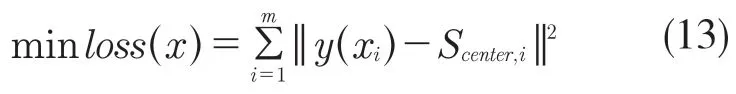
采用迭代法求取使得损失函数取得最小值的参数值αi，βi，γi，便可拟合出功率谱矩心对应的模型。

4 实验分析

本文所使用的验证数据来自辛辛那提大学提供的转速为2 000 r/min，负载约为26 689.2 N 的全寿命轴承实验，该实验采样频率为20 kHz，采样时间为1 s，前期采样间隔为5 min，后采样间隔改为10 min，设备运行至轴承完全失效时停止实验。实验过程中所采用的轴承为Rexnord ZA-2115 双列滚柱轴承，采集的数据分为3 个部分，每部分均采集了4 个轴承的运行情况。本次分析选取其第2 部分实验数据中的第1 个轴承作为分析对象。该实验的相关参数见表1。

表1 辛辛那提轴承实验相关参数Tab.1 Parameters of bearing experiment in Cincinnati Uni.

由于采集的数据含有不同噪声和干扰，会对实验结果产生负面影响，为尽量消除该种弊端，提升对轴承特征的提取精度，提高轴承的性能退化预警精度，需要对原始信号进行滤波降噪。本次实验通过对比EMD 方法和EEMD 方法以后，选择采用EEMD 法通过添加噪声对原始信号进行处理，分解后可得到该信号的本征模函数，如图3 所示。由于使用EEMD 分解之后可以得到14个本征模函数，在此处仅选择其对应的偶数个IMF 分量进行展示。

图3 EEMD 分解后的本征模函数Fig.3 IFMs after EEMD

通过对分解得到的本征模函数进行筛选以后，进行信号重构可以得到原始信号和降噪以后信号的对比。如图4 所示，通过对比分析，该型号波动值有所减小，信号集中度有所下降，因此可以看出EEMD 对该振动信号的降噪效果明显。

图4 信号处理结果对比Fig.4 Signal comparison after processing

轴承1 的信号在经过傅里叶变化以后可得其正常运行时与性能发生退化时对应的频谱图以及功率谱密度图，如图5、图6 所示。通过对应的频谱分析可以看出，轴承1 在正常运转时，其对应基频的幅值和功率占比基本上都在频率较低的区域。然而，对于正在发生性能退化的轴承对应谐波分量的能量值普遍有所上升，且高频分量所占的幅值以及功率增加，这使得频谱的矩心向右移动。

图5 正常运行(左)和性能退化(右)的频谱对比Fig.5 Spectrum comparison between normal running(left) and performance degradation (right)

为了突出所提出特征指标的表征能力，将轴承1 采集的振动信号也进行了时域分析，通过时域常用的分析指标，筛选出了表现能力较强的几个特征，包括振动信号的有效值、峰值指标、裕度指标。如图7 所示，通过对比可以发现，功率谱密度矩心指标可以反映出，轴承在570 min 时，其性能已经开始退化，且后续的退化过程十分直观。然而，时域对应的指标虽然也可以在一定程度上表征轴承1 的退化状态，但是除了RMS 值可以略微检测出570 min 对应的早期退化以外，其余指标几乎不能检测出其早期的退化过程。

图6 正常运行(左)和性能退化(右)的功率谱密度对比Fig.6 Power spectral density comparison between normal running (left) and performance degradation (right)

图7 时域指标和功率密度矩心指标对比Fig.7 Comparison of time domain index and power density centroid index

因此，使用功率谱密度矩心作为特征指标，可以良好地表征轴承的退化状态，且可以较为准确地检验出早期的退化情况，这可以为轴承后期的维保进行预警，为生产车间的工作人员制定维保计划、生产变更预留缓冲期，降低因轴承失效致使生产设备带来的损失。

为进一步增强该指标的退化趋势，随后对上述结果进行高斯模型拟合，拟合结果见图8。可以看出，拟合后的结果基本和上述讨论的结果保持一致，轴承1的退化状态从570 min处开始萌芽，在710 min 和850 min 达到峰值直至轴承失效。

图8 高斯混合模型拟合Fig.8 Gauss Models fitting

5 结论

本文在傅里叶变换的基础之上，将信号对应的能量转换到频域进行分析。在分析其功率谱密度时，将该频域谱对应的矩心值作为性能退化指标，用于表征滚动轴承的退化状况。与此同时，对振动信号也进行了时域的分析，在将时域的信号指标与所提出的指标进行对比之后发现，该矩心指标能够表征滚动轴承早期的退化状态。因而，可以为后续轴承的维保工作提供参考价值，协助工作人员制定维保计划，提升车间的生产效率，降低由于轴承失效带来的经济损失，从而降低生产成本。此后，为增强该指标的性能，采用高斯函数对其进行拟合。综上，通过对辛辛那提给定的数据分析可得，该指标对于轴承性能退化情况的反应性能优良。除此之外，该指标还可用于滚动轴承的寿命预测等方面，也可以通过对该指标的继续研究提升对轴承退化状况的评估和预测。