基于Simulink 软件的组合滑模控制仿真实验

赵海滨，田亚男

（1.东北大学 机械工程与自动化学院，辽宁 沈阳 110819；2.东北大学 信息科学与工程学院，辽宁 沈阳 110819）

滑模控制器具有响应速度快、对参数变化及扰动不灵敏和物理实现简单等优点，广泛用于非线性系统控制[1]。传统的滑模控制器，稳态误差不能在有限时间内收敛到零，从而提出了终端滑模控制的概念。终端滑模控制器能够在有限时间内收敛到零，而且对建模不确定和外部干扰信号具有鲁棒性。快速终端滑模控制器的收敛速度非常快，但是在接近平衡状态时存在奇异问题[2]。本文将快速终端滑模控制器和线性滑模控制器相结合，设计了组合滑模控制器，并采用组合滑模控制器进行二阶Duffing 混沌系统的平衡控制。

本文以二阶Duffing 混沌系统为研究对象，采用组合滑模控制器进行系统的平衡控制，状态变量快速收敛到零。采用Simulink 软件建立仿真实验系统进行仿真实验，并对仿真结果进行分析。组合滑模控制器能够进行不同初始状态Duffing 混沌系统的平衡控制，能够避免奇异问题，具有非常快的收敛速度。

1 二阶非线性系统

二阶Duffing 混沌系统常用于微弱信号的检测[3]，是典型的二阶非线性系统。对于Duffing 混沌系统的控制，已经提出很多方法[4-5]。Duffing 混沌系统的状态方程表示为

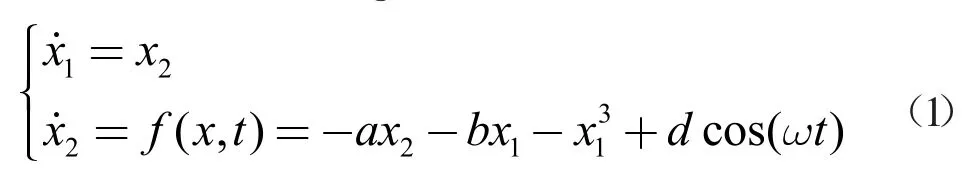
其中，x1和x2为系统的状态变量，t 为时间，a、b、d 和ω 为常数。当a=0.4，b=-1.1，d=1.5，ω=1.7 时，该系统处于混沌状态。

根据Duffing 混沌系统的状态方程，采用Simulink 软件进行仿真，采用变步长的ode45 算法，最大步长为0.001 秒。Duffing 混沌系统的初始状态设定为x1（0）=0.2，x2（0）=0.3，系统的仿真时间设定为300 秒。

Duffing 混沌系统仿真后，状态变量x1和x2的二维相图，如图1 所示，状态变量x1和x2的响应曲线，如图2 所示，只显示前100 秒。由图1 和图2，可以观察到Duffing系统处于混沌状态。

图1 状态变量x1和x2的二维相图

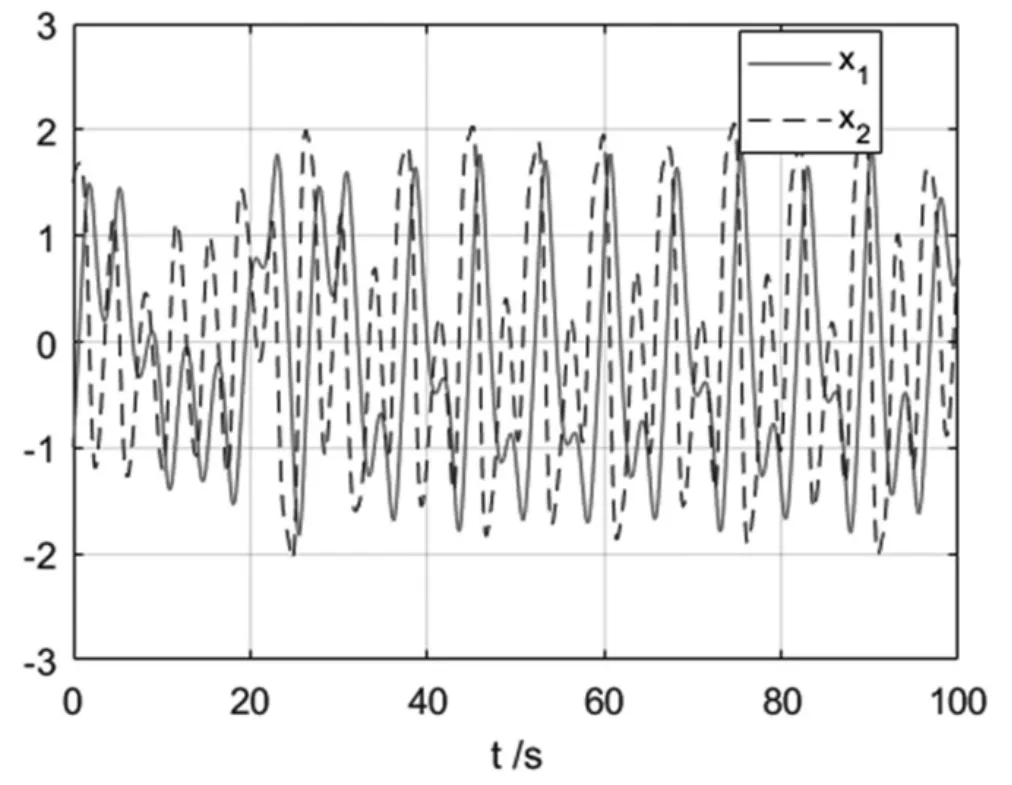
图2 状态变量x1和x2的响应曲线

2 组合滑模控制器

通过快速终端滑模控制器和线性滑模控制器设计组合滑模控制器，采用组合滑模控制器进行二阶Duffing 混沌系统的平衡控制。在快速终端滑模控制器中，设计的快速终端滑模面为

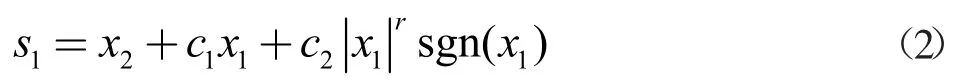
其中，c1，c2和r 为常数，且c1>0，c2>0，0

在快速终端滑模控制器的设计中，采用的指数趋近律为

其中，k1和k2为常数，且k1>0，k2>0。

采用快速终端滑模面和指数趋近律，设计的快速终端滑模控制器为

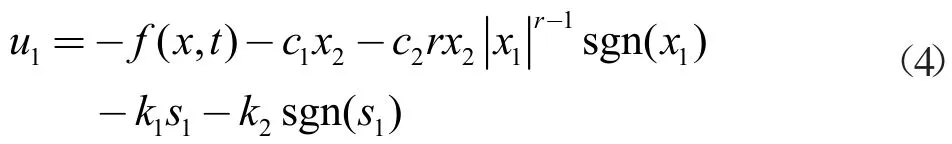
在线性滑模控制器中，采用的线性滑模面为

其中，c3为常数，且c3>0。

在线性滑模控制器的设计中，采用的指数趋近律为

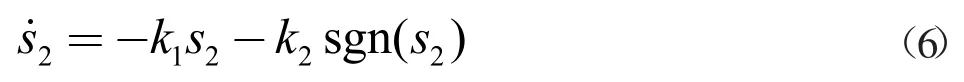
采用线性滑模面和指数趋近律，设计的线性滑模控制器为

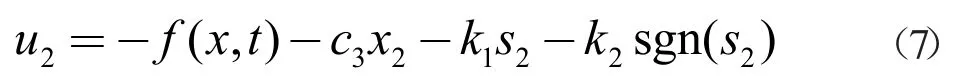
虽然快速终端滑模控制器的收敛速度比较快，但是由于r-1<0，在x1=0 和x2≠0 时快速终端滑模控制器存在奇异问题。首先采用快速终端滑模控制器进行系统的平衡控制，当|x1|燮δ 时，切换为线性滑模控制器。快速终端滑模控制器和线性滑模控制器的切换规则为

其中，u 为组合滑模控制器，δ 为常数，且δ>0。

组合滑模控制器的切换函数表示为

根据组合滑模控制器的切换规则，当采用快速终端滑模控制器时，m=1，当采用线性滑模控制器时，m=2。

在快速终端滑模控制器和线性滑模控制器中，都存在符号函数，会出现抖振现象。本文采用双曲正切函数代替符号函数，用于削弱抖振。双曲正切函数的表达式为

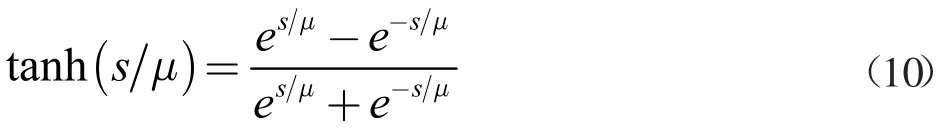
其中，μ 为常数，且μ>0。本文设定为μ=0.001。

3 仿真实验

Simulink 软件非常适合进行动态系统的建模和仿真[6]。采用Simulink 软件进行组合滑模控制仿真实验，建立的仿真实验系统，如图3 所示。在Simulink 软件中采用变步长的ode45 算法进行常微分方程的数值求解[7-8]。Duffing混沌系统的初始状态为x1（0）=1.5，x2（0）=0.6。在快速终端滑模面中，参数设定为c1=2，c2=2.5，r=0.6。在指数趋近律中，参数设定为k1=4，k2=0.6。在切换规则中，参数设定为δ=0.05。

采用组合滑模控制器进行Duffing 混沌系统的平衡控制，仿真时间设置为4 秒，状态变量的响应曲线，如图4 所示，组合滑模控制器的响应曲线，如图5 所示。切换函数的响应曲线，如图6 所示。图6 中在0.91 秒时，将快速终端滑模控制器切换为线性滑模控制器。

数值仿真结果表明，组合滑模控制器能够进行不同初始状态二阶Duffing 混沌系统的平衡控制，状态变量快速收敛到零。

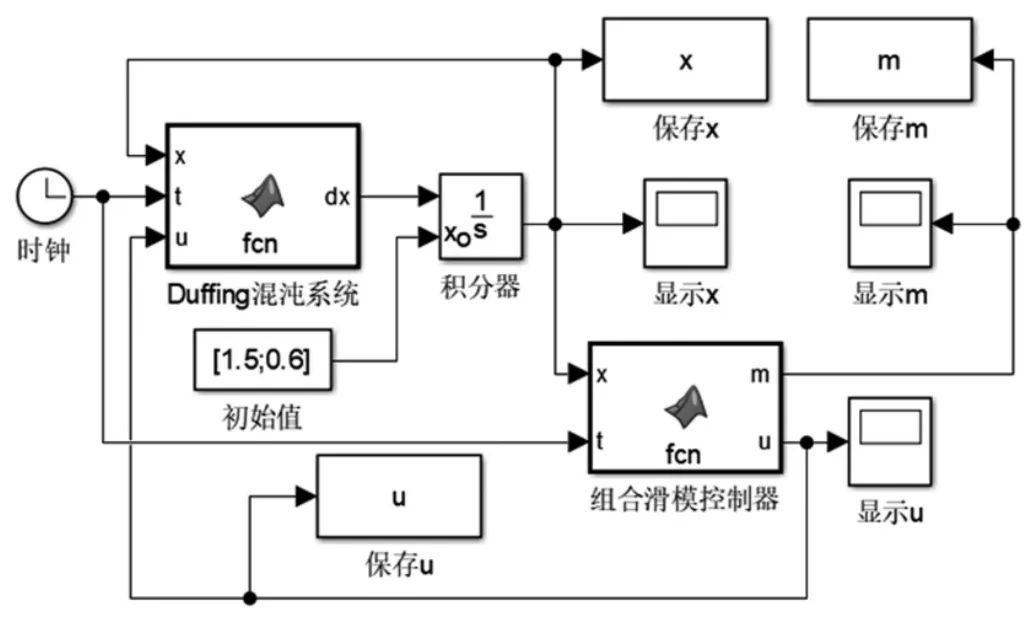
图3 组合滑模控制仿真实验系统

4 结论

本文将快速终端滑模控制器和线性滑模控制器相结合，设计了组合滑模控制器，通过切换规则进行快速终端滑模控制器和线性滑模控制器的切换。采用组合滑模控制器进行二阶Duffing 混沌系统的平衡控制。通过Simulink 软件建立仿真实验系统，并进行了数值仿真。仿真结果表明，组合滑模控制器能够进行不同初始状态Duffing 混沌系统的平衡控制，状态变量快速收敛到零。

图4 Duffing 混沌状态变量的响应曲线

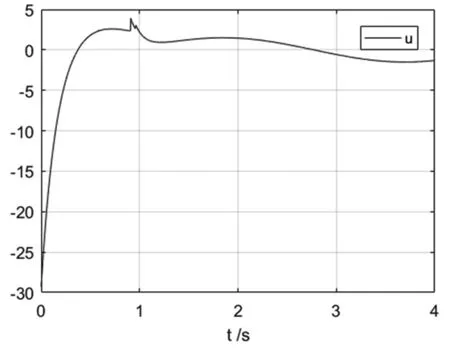
图5 组合滑模控制器的响应曲线

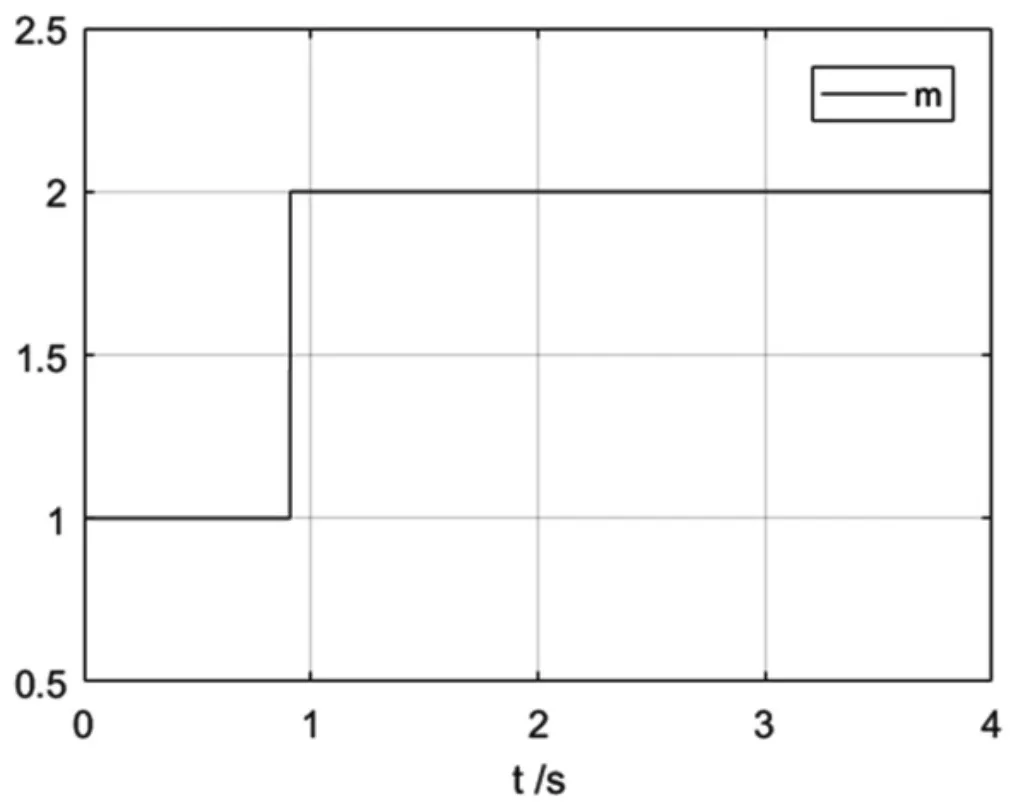
图6 切换函数的响应曲线