压水堆核电站稳压器控制策略研究*

曹华宇，段 宇，谢文俊，于汇辰，郑 旭，徐良晨，张 宇

（南京工程学院 能源与动力工程学院，江苏 南京 211167）

稳压器一回路系统中的压力能够按照设定的工况或者稳定工况及时进行调节，这样才能确保核电站运行的安全性，所以稳压器控制系统将其中的压力调节在指定范围内（工况压力在15.5MPa 附近）就显得尤为重要。同样水位的控制也是如此。传统的PID 控制器不依懒于控制对象的精确模型，具有控制原理简单、容易实现，实用性强的特点，只需要确定比例增益、积分增益、微分增益并进行适当的参数整定即可设计出一个PID 控制器。在机电、化工、机械等行业都有广泛的应用。但是稳压器是一个非线性、时变且易受干扰的复杂系统，由于PID 控制器本身的不足，会使得动态偏差较大导致超调量变大进而影响核电站运行的稳定，且不能满足实时工况的动态调节，控制效果不尽人意，达不到理想要求。因此出现了许多新型的控制策略，例如自抗扰控制器，智能控制，模糊PID 控制等等。本文基于生物的免疫系统设计出免疫PID 控制器并对其进行仿真研究。仿真结果显示，免疫PID 控制器能够提高稳压器压力和水位控制系统的稳定性，减小动态偏差，缩短调节时间，优于传统的PID 控制器。

1 稳压器与常规PID 参数整定

稳压器在压水堆核电站一回路中起着举足轻重的作用，不仅对压力进行实时控制同时又提供超压和低压保护。核电站中常用的稳压器有气罐式和电热喷雾式两种，它们的结构以及原理都不同。气罐式稳压器结构简单，辅助设备少，维护管理更为方便，在早期核电站中广泛使用。但在压缩空气和提高惰性气体的时候易造成泄露，并且易溶于水，从而造成系统和设备的腐蚀，安全性能大大降低。所以为了提高核电站运行的安全性和减少公众对核问题的担忧，如今在大功率核电站中都使用电热喷雾式稳压器[1]。常规PID只需确定比例系数kp、积分系数ki 和微分系数kd 即可，较为简单。其参数整定方法有响应曲线法、临界比例带法、衰减曲线法、试凑法等等。以下主要介绍衰减曲线法，首先使控制器参数积分时间Ti 趋于无穷大，Td=0，比例带δ 置于较大数值，将控制系统投入闭环运行。调整比例带大小直至衰减率Φ=0.75，记录下此时的比例带δs 与振荡过程的周期Ts。

按照δ=0.8δs，Ti=0.3Ts，Td=0.1Ts 计算控制器的参数。

2 免疫PID 控制器的设计

生物的免疫调节能够迅速地清除入侵抗原以保持生物体的健康和发展，是生物体的一种特异性反应。当病毒细菌等抗原侵入机体时，会刺激T 细胞，包括TH（辅助细胞）和TS（抑制细胞），由于抗原浓度较大，TH（辅助细胞）会增多刺激B 细胞，B 细胞会根据抗原产生相应的抗体，消除抗原。当机体内的抗原浓度减小，TH 细胞就会减少；反之TS 细胞就会增多从而抑制B 细胞产生抗体，经过一段时间后，抗原完全消灭，机体达到平衡。

由上述的生物免疫反馈的机制，设计出免疫PID 控制器。假设变量ε（k）：第K 代抗原浓度；TH（K）：由抗原刺激的辅助细胞的输出量；TS（K）：抑制细胞对B 细胞的影响，则B 细胞接受的浓度为[2]：

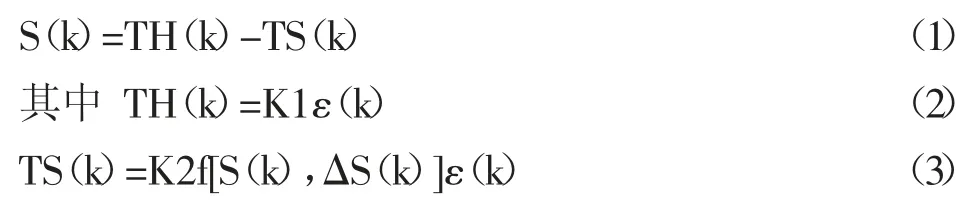
根据（1）（2）（3）式子，得出B 细胞浓度与抗原浓度的关系式为：

其中K=K1 为促进因子，K2 为抑制因子，η=K2/K1 表示TS 和TH 的比例系数；非线性函数f（.）表示细胞抑制刺激能力的大小；△S（k）为B 细胞的浓度变化。

ε（k）相当于第K 个采样时刻给定值与实际输出值的偏差e（k），而B 细胞的浓度S（k）相当于K 时刻的实际输出值u（k）[3]。

从形式上看，免疫控制器是比例系数为K{1-ηf[u（k），△u（k）]}的非线性控制器。结合（5）式和传统的PID 控制器得出免疫PID 控制器，免疫PID 控制器表示为：

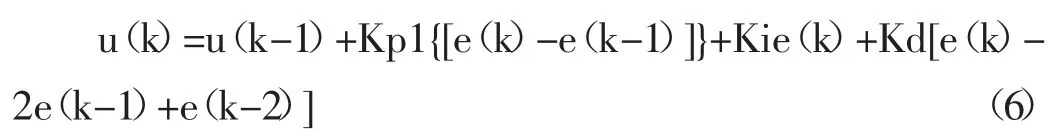
式中：Kp1=K{1-ηf[u（k），△u（k）]}；K 为增益；Kp 为比例系数；Ki 为积分系数；Kd 为微分系数。

由于f（.）函数难以表述，所以本文用两个输入，一个输出的二维模糊控制器来描述f（.）函数。两个输入量为u（k）和△u（k），输出为f（.）函数。每个输入量被P（+）、N（-）模糊化；每个输出量被三个模糊集模糊化，分别为P（+）、Z（0）、N（-），隶属度定义在（-∞，+∞）之间[4]。

根据生物免疫原理可以得到以下模糊规则：

（1）if u is P and △u is P then f（.）is N;

（2）if u is P and △u is N then f（.）is Z;

（3）if u is N and △u is P then f（.）is Z;

（4）if u is N and △u is N then f（.）is P;

3 MATLAB 的仿真与分析

本文以稳压器压力控制系统和水位控制系统为研究对象，它们都是典型的非线性、多时变、大惯性且易受干扰的控制系统。首先通过阶跃响应曲线大致确定传递函数的阶次和类型，然后求得动态特性的特征参数，如放大系数、时间常数、延迟时间等，再利用系统辨识的基本知识，拟合出稳压器水位和压力的传递函数[1]。

其中900MW 机组压力控制系统的传递函数为：

本文采用MATLAB 软件进行免疫PID 与常规PID 的仿真和分析，根据式（7）式（8）得出的传递函数用simulink搭建出的水位控制系统和压力控制系统的仿真模型。仿真模型如图1 和图2 所示。

本文仿真的是容量为900MW 机组的压水堆核电站，输入信号取典型的幅值为1 的阶跃信号，仿真时间分别设定为1000s（水位控制系统），400s（压力控制系统）。根据前面所搭建的仿真模型，分别对免疫PID 控制器和常规PID控制器控制下的仿真曲线进行比较。仿真曲线比较示意图如图3 和图4 所示。

由图3 可得免疫PID 调节的超调量比之前略小，稳定性更好，且较快达到稳定的控制效果，调节时间提前了95s。经过曲线分析说明了免疫PID 较传统PID 相比有更好的调节效果。根据图4 表明，在压力控制系统中，免疫PID 比常规PID 取得了更优的动态调节效果，与传统PID控制器相比，最大动态偏差仅有0.067，调节时间大大减少，经过12s 左右就基本调节完成，稳定性也更好。综上所述，免疫PID 控制器在稳压器压力和水位控制系统中都取得了更好的调节效果。

4 结论

本文以常规PID 为基础，从生物免疫反馈调节入手进行思考，设计出具有自适性的免疫PID 控制器。经过MATLAB 仿真研究表明，免疫PID 控制器具有更好的稳定性且超调量小、响应时间迅速。对于压水堆核电站稳压器这类复杂的、非线性、多干扰的系统具有较好的控制效果。

本文在一些算法和参数的整定中并没有做到最优，例如f（.）函数中模糊规则和仿真模块中的增益设置等等。要想进一步提高控制效果还需要不断地探索和研究。我们要永远保持着探索和研究精神，相信不久，免疫PID 会发展的越来越完善，在更多的领域得到应用。

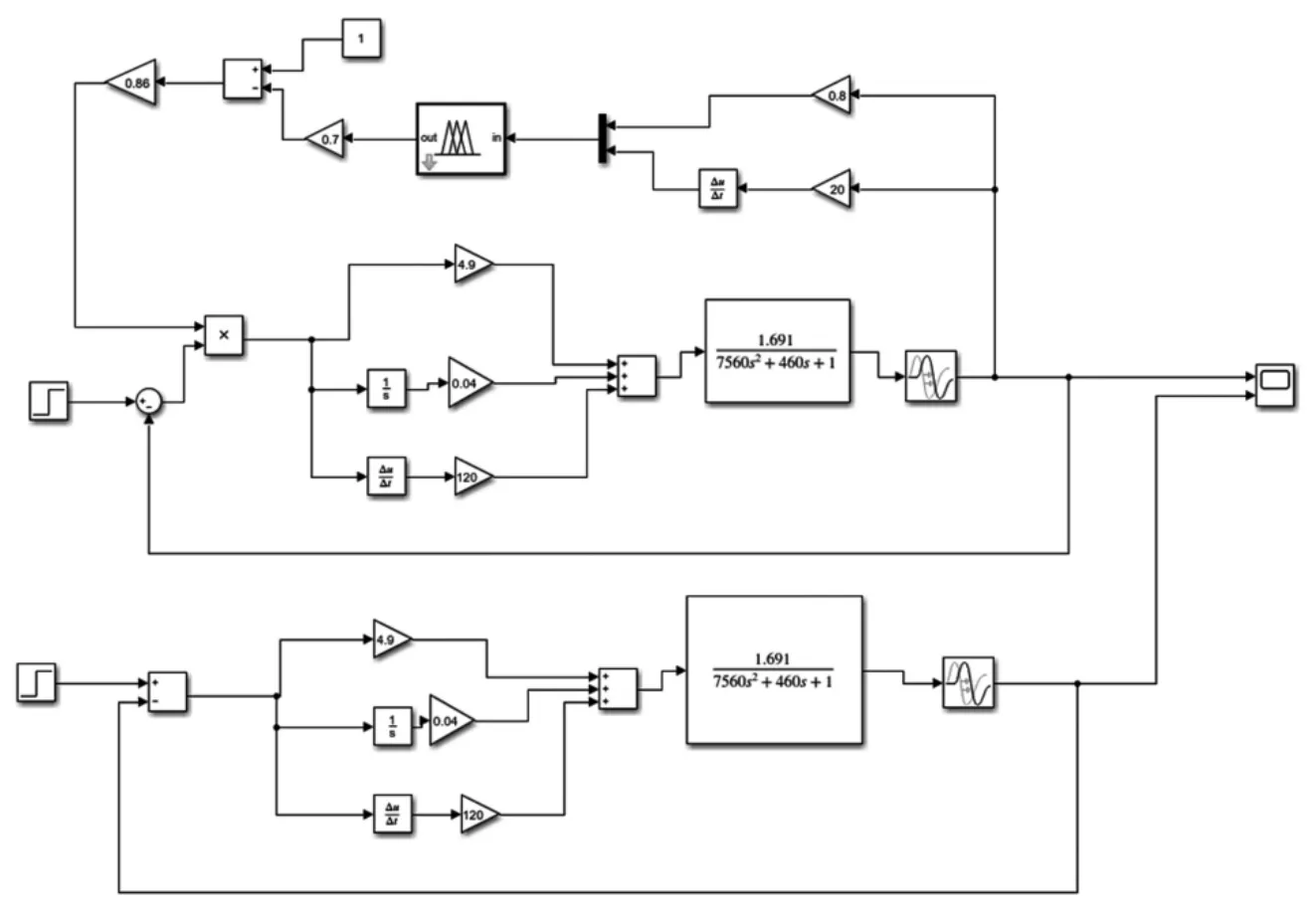
图1 900MW 机组水位仿真模型

图2 900MW 机组压力仿真模型

图3 900MW 机组水位仿真曲线

图4 900MW 机组压力仿真曲线