集装箱托运人意向选择实验设计新方法
陶学宗 诸立超


摘要:
聚焦集裝箱托运人货运选择偏好调查,对意向选择实验(stated choice experiment, SCE)设计方法(问卷设计的核心)进行研究。基于D-error和S-error两个效率指标,提出一种均衡调查效率与调查成本的SCE设计新方法。以义乌至宁波集装箱运输为例,利用试调查数据和新设计方法设计SCE。研究发现:新设计方法的D-error和S-error指标值分别为0.044 3和20,小于传统正交设计法的0.056 2和61;基于新设计方法、正式调查的SWAIT多元Logit模型(multinomial Logit model proposed by SWAIT, MNLS模型)在拟合优度和显著参数数目上均优于基于正交设计法、试调查的MNLS模型。结果表明,新设计方法能够以较小样本量得到拟合优度更好的模型,揭示更多的托运人货运选择偏好信息,可为高效率、低成本地采集托运人货运选择偏好数据提供一种新途径。
关键词:
集装箱运输; 货运方式选择; 意向选择实验(SCE); 高效设计; 托运人
中图分类号: U169.6
文献标志码: A
收稿日期: 2020-02-21
修回日期: 2020-05-09
基金项目: 国家自然科学基金(72074141,71603162);浙江省自然科学基金(LQ21E080023);
浙江省哲学社会科学规划课题(21NDQN256YB)
作者简介:
陶学宗(1981—),男,河南嵩县人,副教授,硕导,博士,研究方向为港口物流、多式联运,(E-mail)xztao@shmtu.edu.cn
通信联系人。(E-mail)zlc1113@126.com
A new design method to stated choice experiments for
container shippers
TAO Xuezong1, ZHU Lichao2*
(1.College of Transport and Communications, Shanghai Maritime University, Shanghai 201306, China;
2.School of Business Administration, Zhejiang University of Finance and Economics, Hangzhou 310018, China)
Abstract:
Focused on the survey of container shippers freight choice preference, the core issue in questionnaire design is studied on how to design the stated choice experiment (SCE). A new SCE design method with balance ability between the survey effeciency and the survey cost is presented according to two efficiency indexes of D-error and S-error. Taking container transport from Yiwu to Ningbo as a case, the SCEs are designed by the pilot survey data and the new design method. It is found that the values of D-error and S-error indexes for the new design method are 0.044 3 and 20, respectively, which are less than 0.056 2 and 61 for the traditional orthogonal design method. The multinomial Logit model proposed by Swait (MNLS model) based on formal survey and the new design method is better than MNLS model based on pilot survey and the orthogonal design method both in goodness-of-fit and the number of significant parameters. The results indicate that, by the new design method, the model with better goodness-of-fit can be obtained with less sample size, and more information on shippers freight choice preference can be revealed. It can provide a new way to data collection of shippers freight choice preference with high efficiency and lower cost.
Key words:
container transportation; freight mode choice; stated choice experiment (SCE); efficient design; shipper
0 引 言
推进港口腹地部分集装箱货物从公路向水路和铁路转移,是港口贯彻绿色发展理念、实现可持续发展目标的战略选择,对打好污染防治攻坚战、打赢蓝天保卫战、推动经济社会高质量发展具有重要意义[1]。在此背景下,急需研究并掌握集装箱托运人的货运选择行为特征,以便识别港口集疏运方式转移的关键影响因素,并为制定和调整港口集疏运转移促进政策提供决策支持。其中,货运选择偏好信息的采集是研究集装箱托运人货运选择行为特征的重要基础。从研究者的角度看,托运人属性[2]、货物属性[3]、地理属性[4]等对托运人货运选择行为的影响日益受到关注,导致研究本身对托运人货运选择偏好数据的需求日趋扩大。从托运人的角度看,他们不愿透露所选货运服务的时间和费用等商业信息,导致托运人问卷调查响应度低、数据完整性较差。因此,采集托运人行为偏好(revealed preference,RP)数据面临着严峻挑战,使得研究者不得不转向采集意向偏好(stated preference,SP)数据[5]。通常情况下,货运SP数据的采集需借助意向选择实验(stated choice experiment,SCE),而SCE的关键是设计假设情景。目前,SCE假设情景的设计主要有变量波动法(文献中未明确定义)和正交设计法。变量波动法指研究者基于既有研究经验,结合托运人访谈和RP调查数据,确定货运服务各属性的合理取值区间,然后在取值区间内选取若干水平,对不同货运方式的不同属性水平进行组合,从而得到假设情景[6]。正交设计法通过均衡搭配不同变量及其取值水平,减少假设情景数,提高设计效率,但可能生成某一货运方式所有属性均占优的假设情景,目前仅有少部分学者使用[7-8]。然而,这两类方法存在以下问题:①所采集数据存在信息冗余,即采集到的某些信息可以从其他信息推导出来,导致调查效率降低;②为保证参数显著性,需要更多样本量,导致调查成本上升。不仅如此,国内外几乎所有相关研究都未说明所采集的样本量是否足够用于建模分析[5]。鉴于此,本研究基于D-error和S-error两个设计效率指标[9-10],提出一种均衡调查效率与调查成本的SCE设计新方法,并以义乌至宁波集装箱运输为例,验证该方法的有效性。需要说明的是,D-error和S-error两个指标是针对SCE情景设计提出的,而RP调查无须设计情景,因此不涉及此类指标。
1 SCE设计新方法
SCE设计新方法的核心在于均衡调查效率与调查成本。在样本规模相同时,模型统计有效性越好(拟合优度值较大,且满足一定显著性要求的参数数目较多),调查效率越高。在统计上,调查效率可用D-error指标[9]进行度量,其值越小,调查效率越高。在模型统计有效性相同或接近时,标定模型所需样本规模越大,调查成本越高。在统计上,调查成本可用S-error指标[10]进行度量,其值越小,调查成本越低。D-error和S-error指标值都可以从模型的渐近协方差(asymptotic variance covariance,AVC)矩阵推导出来。因此,SCE设计新方法的本质就是,基于货运方式选择模型的AVC矩阵寻求D-error指标值最小的高效率假设情景,并在此基础上寻求满足显著性要求的最小样本规模。
1.1 基于Logit模型的AVC矩阵
Logit模型是货运方式选择行为研究领域应用最广泛的模型[11]。假设托运人
n(n=1,2,…,N)在假设情景s(s=1,2,…,S)选择货运方式j(j=1,2,…,J)的效用确定项为Vnsj,则Vnsj可由货运方式属性xnsjk与对应参数βk的线性组合Kk=1(βkxnsjk)表示,其中k为货运方式属性编号,k=1,2,…,K。根据Logit模型建模理论[12],托运人n在假设情景s选择货运方式j的概率为
式中:δnsj为指示变量,当托运人n在假设情景s选择货运方式j时δnsj=1,否则为0。
Logit模型相應的对数似然函数和费雪信息矩阵分别为
式中:Z为由znsjk组成的NSJ×K维矩阵;znsjk为矩阵Z的元素,其值取决于货运方式属性xnsjk、货运方式数目J和选择概率Pnsj。
根据Logit模型导出的AVC矩阵为
1.2 调查效率衡量指标D-error
D-error指标值的计算公式[9]为
式中:M为矩阵ΩN的秩,即模型的待估参数数目。
D-error指标值为AVC矩阵行列式的M次方根,其最小值对应的SCE设计称为D-optimal设计[12]。在设计假设情景时,随着变量数和水平数的增加,潜在情景组合数呈指数增长。例如,假设集装箱托运人可选的货运方式有2种(公路和铁路),且每种货运方式均可通过运输时间、运输费用和时间波动变量描述,3个变量均有3个水平,则一共有(33)2=729种假设情景。在满足数据采集需求和集装箱托运人可接受条件下(如每张问卷18个假设情景),为从729种假设情景中找出使D-error指标值最小的假设情景组合,则需要进行
729!/(18!(729-18)!)≈4.27×1035次计算。面对如此庞大的计算量,很难保证在有限时间内找到D-error指标值最小的SCE设计。鉴于此,在实践中通常采用D-error指标值相对较小的SCE设计,即D-efficient设计[12]。在D-efficient设计实践中,一般借助由悉尼大学商学院开发的专用SCE设计软件Ngene [13]或自己编写MATLAB程序完成。
1.3 调查成本衡量指标S-error
目前,货运方式选择行为相关领域的绝大部分研究者对模型参数估计所需样本量知之甚少,通常希望样本量足够大以产生可靠的参数估计值,导致调查成本居高不下。为此,ROSE等[10]提出了S-error指标用于确定建模分析所需的最小样本规模,从而降低调查成本。
假设模型待估参数值为β,参数先验值为β,用sN(β)表示样本量为N时的參数估计值渐近标准差,其为矩阵
ΩN的对角元素平方根。为便于SCE设计,通常假设每一托运人面临的假设情景数目相同,即
IN=N·I1。因此,ΩN=
I-1N=Ω1/N,这就意味着
假设s1(β)=1,根据式(6)可确定模型参数估计值标准差
1/N的变化规律,见图1。
从图1可以看出,只有将样本量增加至原来的4倍时,相应标准差才能减小一半。因此,当样本量较大时,样本量增加所带来的标准差减小量符合边际递减原理,即标准差的减小需要更多样本量。盲目增加样本量,不仅增加调查成本,而且很可能效果甚微,而新设计的目标是整体下移这一标准差变化曲线,更加有效地减少建模所需样本量。
基于式(6),可借助渐近t检验确定最小样本量。为保证参数估计值在φ(90%、95%、99%)置信水平上与0存在显著差异,应满足
式中:tφ为置信水平φ(90%、95%、99%)对应的临界值(1.65、1.96、2.56)。
式中:Nk,φ为待估参数β*k满足φ置信水平时对应的最小样本量。
当所有参数估计值满足在φ置信水平上显著时,最小样本量中的最大值即为S-error指标值,具体按式(9)计算:
式中:Se,φ为φ置信水平对应的理论最小样本规模。
在正式调查中,考虑到无应答误差、编码和录入误差等问题,需对理论最小样本规模进行修正。根据文献[5]的测算,修正系数为1.103。
2 基于SCE设计新方法的调查问卷设计
2.1 参数先验值确定
考虑到义乌集装箱运输需求规模大,且课题组具有一定研究基础,选取义乌至宁波的集装箱运输(目前主要采用公路和铁路2种货运方式)为研究对象,采集义乌集装箱托运人货运选择偏好数据。课题组于2014年9月10日至12日对义乌当地集装箱托运人开展一对一访谈和问卷调查,调查内容涵盖托运人属性、货物属性和SP假设情景选择等。由于对拟研究变量对应的参数值缺乏先验认知,故通过正交设计法得到若干假设情景,随机挑选15个假设情景进行试调查。
鉴于运输时间阈值对集装箱托运人货运方式选择的影响,构建分段效用函数的多元Logit模型。其中,阈值指集装箱托运人对某一属性可接受的最大或最小值。一旦某一货运方式的某一属性超过或低于阈值,无论其他属性多好都难以补偿这一属性带来的损失,托运人就很可能不选择这一货运方式[7]。该模型由SWAIT[14]
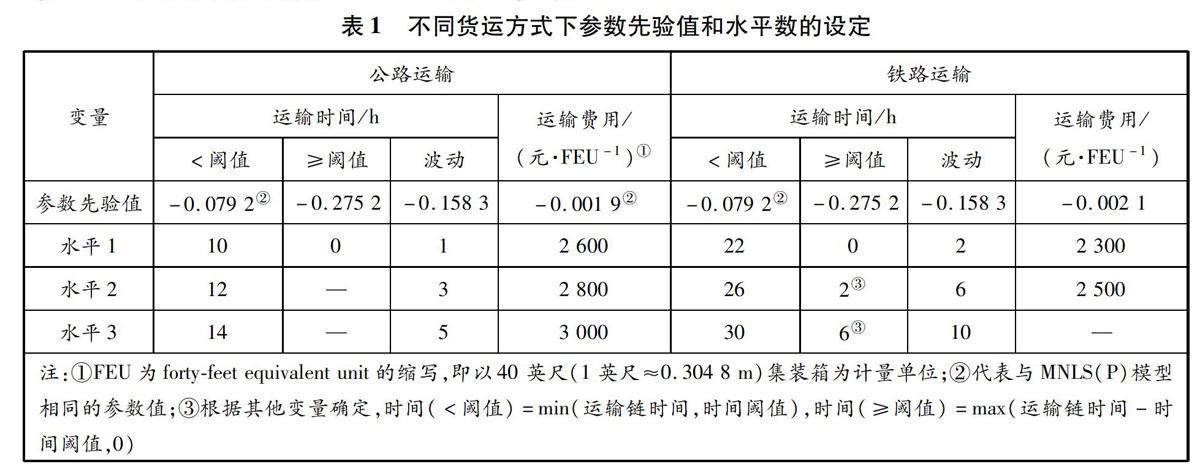
提出,故将其称为SWAIT多元Logit模型。利用计量经济学专用软件包NLogit 6.0对基于试调查的SWAIT多元Logit模型(multinomial Logit model proposed by SWAIT for pilot survey,MNLS(P)模型)参数进行估计,然后对参数估计值进行修正,作为正式调查的参数先验值。具体修正思路如下:①考虑到铁路运输时间价值可能比公路的低,适当增大铁路费用系数,降低其运输时间价值;②为检验超过运输时间阈值的时间价值的确很高和检验参数先验值在潜在错误定义下的D-efficient设计的鲁棒性,将MNLS(P)模型的运输时间阈值参数先验值缩小至原来的1/4;③与运输时间相比,运输时间波动对集装箱托运人货运方式选择的影响可能更大,将运输时间波动参数先验值设置为时间的2倍。最后设定的参数先验值和水平数见表1。
2.2 假设情景生成
考虑集装箱托运人对假设情景数的可接受程度,结合试调查情况和相关文献[5],最终设定18个情景。然后,应用正交设计和D-efficient设计,分别得到不同的假设情景组合。需要注意的是,在绝对占优(某一货运方式在各属性上明显优于另一货运方式)情景中,绝对占优货运方式的分担率将接近1。本研究涉及的两种货运方式的属性各有优劣,不存在某一货运方式属性绝对占优的情况。此外,KANNINEN[15]证明了效用平衡(两种货运方式效用或分担率相近)对实验设计效率并不重要。因此,不能根据两种货运方式分担率差距大小判断设计的优劣。
在本研究中,集装箱托运人SCE设计新方法分为两个阶段:①最小化D-error指标值,在模型参数整体层面保证费雪信息最大化;②计算使每个参数在90%(或95%,99%)置信水平上显著的理论最小样本规模,从中选择最大值作为S-error指标值,以确保所有参数估计值显著。本研究设定置信水平为90%,通过MATLAB编程实现正交设计,利用Ngene完成D-efficient设计。最终得到正交设计和D-efficient设计的SP假设情景,见表2。正交设计的D-error指标值为0.056 2,相应S-error指标值为61;D-efficient设计的D-error指标值为0.047 4,相应S-error指标值为20。由此可见,D-efficient设计在调查效率和调查成本上均优于正交设计。在正式调查中,正交设计和D-efficient设计所需的修正最小样本规模分别为68(≈61×1.103)和23(≈20×1.103)。与正交设计相比,D-efficient设计可节省45个样本(节省率为66.18%)。
2.3 非SCE定量属性的选择
考虑到集装箱托运人在选择货运方式时受到货运服务属性、托运人属性、货物属性等诸多因素影响,本研究结合前期调查经验和现有相关研究[2-5],在确定运输时间、运输费用、时间波动等货运服务属性的基础上,再选取员工数量、成立年限、托运频次、集卡数量、时间阈值、费用阈值等托运人属性,货物批量、货物价值、货物质量等货物属性,纳入集装箱托运人调查问卷中。调查问卷涉及的这些非SCE定量属性的含义见表3。
3 结果分析
3.1 原始数据统计
2015年7月21日至24日,課题组对义乌集装箱托运人进行了正式调查,共采集到30个有效样本(实际抽样率0.86%>抽样率下限0.60%)。每份问卷包含18个SP假设情景,共采集540组数据。剔除严重不完整数据和明显存在瑕疵的数据,最终得到可用数据489组,原始数据的统计结果见表3。
统计结果表明:义乌至宁波的公路集装箱平均运输时间较短,费用稳定,运输时间波动范围较小;义乌市集装箱托运人的企业规模偏小(平均为16.43人),平均成立年限较短(6.3 a),平均托运频次较高(29.88次·月-1),自有集卡数量不多(平均为9.33辆),托运人可接受的时间上限和费用上限的均值分别为25.62 h和2 505元·FEU-1;义乌市
集装箱托运人的单次托运货物批量不大(3.08 FEU·
次-1),附加值较高(25.05万元·FEU-1),货物平均质量为19.8 t·FEU-1(为轻货)。
3.2 建模分析
利用NLogit 6.0对基于正式调查的SWAIT多元Logit模型(multinomial Logit model proposed by SWAIT for formal survey,MNLS(F)模型)参数进行估计,并按照反向逐步选择原则[12]逐步剔除不显著的变量,最终确定MNLS(F)模型的效用函数(见下式),并得到参数估计结果(见表4)。为便于比较,表4还给出了MNLS(P)模型的参数估计结果。
式中:U为效用;n为被调查托运人编号;下标中的1表示公路运输,下标中的2表示铁路运输;ε为效用不可观测项;β为待估计参数;Ac为与运输方式相关的待估常数项;xUtt为运输时间阈值;其余变量见表4。
从表4可以看出,基于D-efficient设计的MNLS(F)模型,其拟合优度值为0.411,大于基于正交设计的MNLS(P)模型的拟合优度值(0.153),说明MNLS(F)模型在整体性能上优于MNLS(P)模型。也就是说,基于D-efficient设计的MNLS(F)模型能够更好地与数据拟合,在实践中有助于提高分析结果的准确性。以支付意愿为例,在未超过时间阈值时,MNLS(P)模型得到的值为41.88元
·FEU-1·h-1,明显大于MNLS(F)模型得到的17.87元·FEU-1·h-1,而根据实际调研测算的支付意愿为13~19元·FEU-1·h-1。由此可见,利用MNLS(F)模型得到的支付意愿更接近实际情况,可有效避免MNLS(P)模型存在的支付意愿被高估的问题。其次,MNLS(F)模型中达到显著性要求的参数有9个,比MNLS(P)模型的多4个,说明MNLS(F)模型能揭示集装箱托运人更多的货运选择偏好信息。以时间波动为例,MNLS(P)模型无法揭示该因素对托运人选择偏好的影响,而MNLS(F)模型表明该因素对托运人选择偏好有负向影响,即某一运输服务的时间波动越大,托运人越不愿意选择这一运输服务,这与实际情况(铁路运输时间波动大,托运人选择少)完全一致。此外,MNLS(F)模型参数先验值的S-error指标值为20,修正最小样本规模为23;参数后验值的S-error指标值为16,修正最小样本规模为18。实际采样规模为30(根据变量波动法实践经验,一般SP调查至少需采集30个样本才能满足建模分析需要),无论是从参数先验值还是从参数后
验值角度看,均足以保证模型参数的显著性。与根据变量波动法使用经验确定的样本规模相比,新设计方法可节省7~12个样本(节省率为23%~40%)。
4 结 论
基于D-error和S-error两个效率指标,提出一种均衡调查效率与调查成本的意向选择实验(SCE)设计新方法,并以义乌至宁波集装箱运输为例进行了实证分析,主要结论如下:(1)SCE设计新方法在调查效率和调查成本上均优于正交设计法;(2)与基于正交设计法、正式调查的SWAIT多元Logit模型(MNLS(F)模型)相比,基于新设计方法的MNLS(F)模型在拟合优度和解释能力方面更加优越,实用性更好;(3)与基于正交设计法和变量波动法实践经验确定的样本规模相比,SCE设计新方法可分别节省45个和7~12个样本。
参考文献:
[1]陶学宗, 吴琴, 尹传忠. 绿色交通目标下集装箱“公转铁”的CO2减排潜力评估[J]. 气候变化研究进展, 2019, 15(6): 660-669. DOI: 10.12006/j.issn.1673-1719.2019.027.
[2]FEOM, ESPINO R, GARCA L. A stated preference analysis of Spanish freight forwarders modal choice on the south-west Europe motorway of the sea[J]. Transport Policy, 2011, 18: 60-67. DOI: 10.1016/j.tranpol.2010.05.009.
[3]ARUNOTAYANUNK, POLAK J W. Taste heterogeneity and market segmentation in freight shippers mode choice behaviour[J]. Transportation Research Part E: Logistics and Transportation Review, 2011, 47: 138-148. DOI: 10.1016/j.tre.2010.09.003.
[4]FEO-VALEROM, GARCA-MENNDEZ L, SEZ-CARRAMOLINO L,et al. The importance of the inland leg of containerised maritime shipments: an analysis of modal choice determinants in Spain[J]. Transportation Research Part E: Logistics and Transportation Review, 2011, 47: 446-460. DOI: 10.1016/j.tre.2010.11.011.
[5]诸立超. 国际集装箱内陆段货运决策模型及竞争力分析[D]. 上海: 同济大学, 2017.
[6]MASIEROL, HENSHER D A. Analyzing loss aversion and diminishing sensitivity in a freight transport stated choice experiment[J]. Transportation Research Part A: Policy and Practice, 2010, 44(5): 349-358. DOI: 10.1016/j.tra.2010.03.006.
[7]张戎, 诸立超. 考虑时间阈值的铁路运输链分担率模型[J]. 交通运输系统工程与信息, 2016, 16(2): 132-138. DOI: 10.16097/j.cnki.1009-6744.2016.02.021.
[8]KANGK, STRAUSS-WIEDER A, EOM J K. New approach to appraisal of rail freight projects in South Korea: using the value of freight transit time savings[J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2159(1): 52-58. DOI: 10.3141/2159-07.
[9]BLIEMERM C J, COLLINS A T. On determining priors for the generation of efficient stated choice experimental designs[J]. Journal of Choice Modelling, 2016, 21: 10-14. DOI: 10.1016/j.jocm.2016.03.001.
[10]ROSEJ M, BLIEMER M C J. Sample size requirements for stated choice experiments[J]. Transportation, 2013, 40: 1021-1041. DOI: 10.1007/s11116-013-9451-z.
[11]张戎, 陶学宗. 托运人货运服务选择行为模型研究述评[J]. 同济大学学报(自然科学版), 2013, 41(9): 1384-1391. DOI: 10.3969/j.issn.0253-374x.2013.09.017.
[12]HENSHERD A, ROSE J M, GREENE W H. Applied choice analysis[M]. 2nd ed. Cambridge: Cambridge University Press, 2015.
[13]ChoiceMetrics. Ngene 1.1.2 user manual & reference guide[M]. Sydney: ChoiceMetrics Pty Ltd, 2014.
[14]SWAITJ. A non-compensatory choice model incorporating attribute cutoffs[J]. Transportation Research Part B: Methodological, 2001, 35: 903-928. DOI: 10.1016/S0191-2615(00)00030-8.
[15]KANNINENB J. Optimal design for multinomial choice experiments[J]. Journal of Marketing Research, 2002, 39: 214-227. DOI: 10.1509/jmkr.39.2.214.19080.
(編辑 赵勉)

