考虑复杂气象变化的智能船舶动态航线规划方法

吴恭兴　王凌超　郑剑　汪超

摘要：

鉴于恶劣海况将引起船舶失速、剧烈横摇甚至倾覆，为避开恶劣海况区域，提出一种考虑复杂气象变化的智能船舶动态航线规划方法。通过改进A*算法的启发式函数，将风、浪对船舶失速的影响加入路径代价值的估算中，进而规划出一条避开恶劣海况的动态航线。跨北大西洋的航线规划仿真结果表明：本文提出的动态航线规划方法可以将船舶的跨洋航行时间缩短18.17%，并且能有效地避开风浪较大的危险海域。运用该动态航线规划方法能缩短船舶航行时间，节约航行成本，提高航运企业的经济效益。

关键词：

动态规划; 航线优化; 气象要素; A*算法; 智能船舶

中图分类号：  U661.32+2; TP273

文献标志码：  A

Dynamic route planning method for intelligent ships considering

complex meteorological changes

WU Gongxinga，b， WANG Lingchaob， ZHENG Jianc， WANG Chaob

（a.College of Ocean Science and Engineering; b.Merchant Marine College;

c.School of Transport & Communications， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

In view of the fact that the severe sea conditions will cause ships to stall， roll violently and evencapsize， in order to avoid the severe sea condition areas， an intelligent ship dynamic route planning method that takes into account complex meteorological changes is proposed. By improving the heuristic function of the A* algorithm， the influence of wind and wave on ship stall is added to the estimation of the path cost value， and a dynamic route to avoid severe sea conditions is planned. The simulation result of the route planning across the North Atlantic shows that the application of the dynamic route planning method proposed in this paper can shorten the sailing time of ships across the ocean by 18.17%，and can effectively avoid the dangerous sea areas with large wind and waves. Using this dynamic route planning method can shorten the sailing time， save the shipping cost， and improve the economic benefit of shipping companies.

Key words：

dynamic planning; route optimization; meteorological element; A* algorithm; intelligent ship

收稿日期： 2020-11-01

修回日期： 2020-12-02

基金項目：

国家自然科学基金（51309148，51709166）;上海海事大学基金（20130433）

作者简介：

吴恭兴（1983—），男，江西广昌人，讲师，博士，研究方向为船舶操纵与控制，（E-mail）wugx@shmtu.edu.cn

0 引 言

目前，国际贸易中85%以上货物的运输是通过海运完成的[1]，然而随着全球气候不断变暖，极端天气出现的频率逐渐升高，海难事故屡屡发生。调查结果显示，从20世纪90年代至今，恶劣气象环境所导致的船体、货物损毁事故数占船舶事故总数的33%，即恶劣海况已成为船舶受损的主要原因[2]。另外，智能船舶技术的开发，应考虑船舶在海上气象变化情况下的动态航线规划，在保证船舶航行安全的前提下，减少智能船舶在风浪中的航速损失，提高航运企业的经济效益。

船舶航速会受到风浪环境的影响[3-4]，因此，在规划船舶航线时，需要考虑海上气象条件。在蒲福风级达到6级时，与静水航行相比，船舶迎风航行的失速高达12%，其发动机功率增加80%[5]。船舶航向与波浪方向通常存在夹角，极有可能导致船舶产生横摇、侧倾等现象，从而引起船舶阻力增加。考虑海上气象条件的船舶航线规划方法大致包括3类：传统方法、智能算法（仿生学算法）和图形学方法。传统方法是根据大量的气象文献资料和前人宝贵的航海经验提出的航线规划方法，其中最早的是由James提出的等时线法，通过对时间进行优化得出一条油耗最低的路径。2013年，ROH[6]对等时线法进行了改进，解决了其难以避开障碍物和“等时线环”的问题;同年，LIN等[7]提出一种三维修正等时线法，该方法利用递归思想和浮动网格系统，以航程权重为状态变量进行船舶航线优化。

智能算法是通过对大自然中各种生命体行为活动的观察而总结出来的算法，具有代表性的有遗传算法、神经网络算法、蚁群算法和粒子群优化算法等。曹永恒[8]将最短路径作为期望优化目标，应用粒子群优化算法解决了复杂的非线性航线优化问题。SZLAPCZYNSKA[9]提出一种多目标天气路径算法，将遗传算法的种群迭代发展过程应用到路径算法中得到一组最优解。TSOU等[10]将蚁群算法与遗传算法结合，利用遗传算法的优势解决蚁群算法局部最优的问题，使优化后的航线能够尽可能避开大风浪区域，并将航行时间和油耗降至最低。随博文等[11]在Q学习算法中融合深度学习理论，有效地解决了维度灾难问题，成功提出一种水面无人艇避障路径规划算法。

图形学方法是一种基于环境建模的航线规划方法，该方法通过将航行环境栅格化，再结合相应算法对航行路径进行优化。其中Dijkstra算法是经典的图形学算法，被广泛应用于解决航线规划问题[12]。SEN等[13]利用栅格法建模求解船舶最优路径问题，采用改进Dijkstra算法，提出一种通用的天气路径算法。ZACCONE等[14]展示了一种基于三维动态规划的船舶航线优化方法，该方法根据天气预报图选择船舶的最佳航向和航速剖面，并将船舶航行参数转化为一个多阶段决策过程，从而形成一个动态规划优化问题。梅斌等[15]提出一种基于正轴等距方位投影的直接求解算法，用于计算船舶偏航距离。陈智康等[16]将蚁群算法中的信息素思想引入Dijkstra算法中，以实现机器人路径规划。潘明阳等[17]从加入约束条件、优化代价函数和优化估价函数3个方面对A*算法进行改进并将其应用于内河水网的航线规划中。秦操等[18]在A*算法的基础上考虑操纵性、静态和动态障碍物和国际海上避碰规则约束，提出一种慎思型避碰轨迹规划算法。

综上所述，现有的船舶航线规划研究大都集中在最优气象条件下的航线搜索算法，而优良的航线规划并非只考虑规避静态障碍物，因为远洋航线不是短期航行，通常一条远洋航线的行程需要一个月甚至更长的时间，在此期间海上气象条件可能发生巨变，而恶劣的天气不仅会使船舶失速、延误航期，而且会严重威胁人员及货物的安全。因此，本文提出一种考虑复杂气象变化的智能船舶动态航线規划方法，在A*算法的启发式函数中加入风、浪对船舶失速的影响，使得规划的航线避开风浪较大的海域;同时，随着智能船舶的航行和海上气象的变化，该算法将根据最新的气象条件实时动态规划最优的航线。

1 风、浪导致的船舶失速计算

1.1 风对船舶失速的影响

风速对船舶航速的影响比较难确定。在小风条件下，船舶在逆风中损失速度，在顺风中略微增加速度。

在大风条件下波浪作用增强，船舶在迎风和顺风中的速度都会降低。大风对船舶航速的影响主要与受风面积和风速大小有关。2004年CHIANG提出计算风对船舶失速影响的公式[19]：

vWS=vWC1γ1A′C2γ2B′（1）

式中：vWS为由风引起的船舶失速;vW为风速;C1和C2分别为空气和海水阻力系数;

γ1和γ2分别为空气和海水密度;A′和B′分别为船体在水线以上和水线以下的侧投影面积。

1.2 浪对船舶失速的影响

船舶在大风浪中航行时，螺旋桨露出水面造成螺旋桨推力减小;波浪作用使船舶转向，从而导致航行阻力增加，最终使得船舶航速降低。影响船舶航速的

波浪参数主要是波高和波向。1967年苏联中央海运科学研究院提出计算波浪对船舶失速影响的公式：

v=v0-（0.745h-0.257qh）×

（1-1.35×10-6Dv0）   （2）

式中：v为船舶实际航速;v0为船舶在静水中的航速;h为波高;q为波向与船舶航向的夹角;D为船舶的排水量。该公式适用于排水量在[5 000，25 000] t范围内且航速在[9，20] kn范围内的船舶。

2008年PANIGRAHJ利用航速与波浪特性之间的关系估算了船舶的实际航速：

v=v0-（μ1+μ2cos q）h（3）

式中：μ1和μ2为由船型决定的常系数。

1.3 风、浪共同作用对船舶失速的影响

在船舶实际航行过程中，风和浪对航速的影响其实是密不可分的，单纯研究风或者浪对船舶失速的影响得到的结果是不精确的。因此，1991年杨振忠等[20]根据大量实船测试资料在考虑了浪的影响的公式中加入风速的影响：

v=v0-（a1h+a2h2+a3D1/3vW-a4qh）×

（1-a5Dv0）    （4）

式中：am为由船型决定的系数，m=1，2，…，5。

式（4）虽然考虑了风速的影响，但是没有考虑风向与船舶航向之间的夹角。1992年刘烽[21]在计算公式中加入了风向的影响，并且给出详细的实船验证结果：

v=v0-（a1h-a2qh+a3vWcos δ）×

（1-a4Dv0）（5）

式中：δ是风向与船舶航向的夹角。

2 基于A*算法的最优航线搜索算法

2.1 A*算法原理

Dijkstra算法是从起点开始通过不断扩散的方式遍历整个图，然后用逆推法找到一条最短路径的，计算量极大，搜索时间很长。A*算法在Dijkstra算法的基础上加入一个启发式函数（如曼哈顿距离），用来指导搜索方向向目标点靠近，搜索区域大幅度减少，并能在极短的时间内找到一条最短路径。在用A*算法搜索路径时，需要用到价值函数：

F（i）=G（i）+H（i）（6）

式中：i为当前节点;

F（i）为从起点到目标点的总移动代价值;G（i）为从起点到当前节点的移动代价值;H（i）为从当前节点到目标点的移动代价值。

本文基于电子海图数据信息，提取多边形障碍物绘制地图，取1°×1°精度进行栅格化。取每个栅格

的中心点为

一个节点。节点k与l之间的距离L采用大圆航线距离公式计算：

L=Rarccossin βksin βl+

cos βkcos βlcos（εk-εl）

（7）

其中：R为地球的平均半径（取6 371km）;βk和εk分别为节点k的经度和纬度;βl和εl分别为节点l的经度和纬度。

用A*算法在经过上述处理的海图中搜索最优航线。

为

描述A*算法的原理，将2个水平或垂直相邻的节点之间的距离设置为1，将2个对角线相邻的节点之间的距离设置为1.4。如图1所示，

空心圓点代表起点，实心圆点代表目标点，空心方块代表待搜索方向上的节点，黑色实心方块表示障碍物，每个方格内的3个数字分别代表此节点的F、G和H值，线条为最终规划路径。

A*算法的执行流程如下：

（1）设置起点A和目标点B，从起点A开始，把A放入一个由节点组成的openlist（openlist是一个待检查列表）中，作为当前节点。

（2）判断当前节点的上下左右4个节点是否为可航行点，是则进行4方向搜索，否则进行8方向搜索。

（3）将当前节点周围的节点加入openlist中，并将点A放入closelist中。

（4）计算openlist中每个节点的F值，选取F值最小的节点作为当前节点，将其他7个节点放入closelist中，并将当前节点放入resultlist中。

（5）重复如下3步：①找出openlist中F值最小的节点，将此节点作为当前节点;②将当前节点放入resultlist中;③按顺序判断与当前节点相邻的所有节点。

（6）在上述过程中若该节点已经在resultlist中，则忽略该节点;若openlist中存在目标点，则停止寻路。

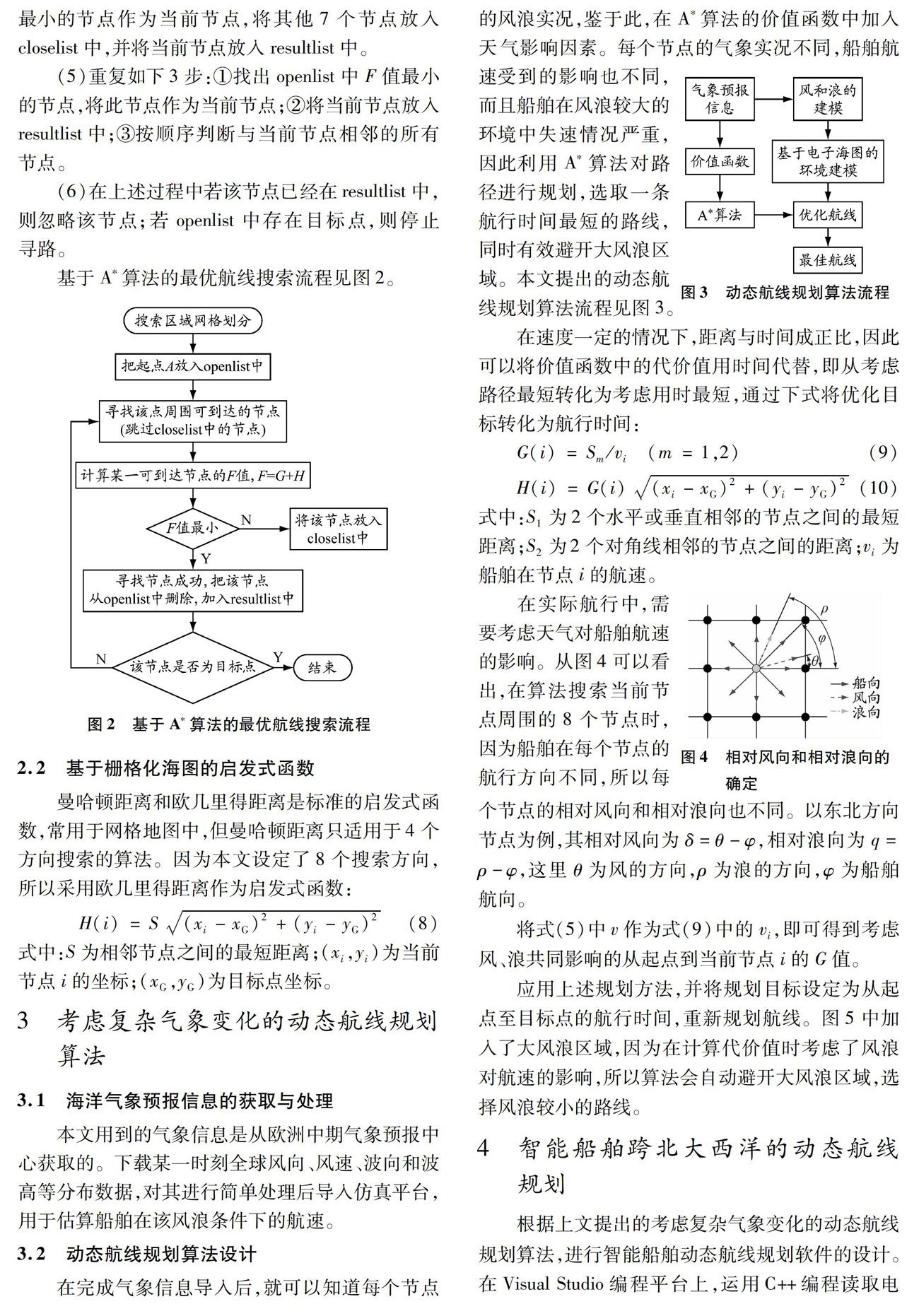
基于A*算法的最优航线搜索流程见图2。

2.2 基于栅格化海图的启发式函数

曼哈顿距离和欧几里得距离是标准的启发式函数，常用于网格地图中，但曼哈顿距离只适用于4个

方向搜索的算法。因为本文设定了8个搜索方向，所以采用欧几里得距离作为启发式函数：

H（i）=S（xi-xG）2+（yi-yG）2（8）

式中：S为相邻节点之间的最短距离;（xi，yi）为当前节点i的坐标;（xG，yG）为目标点坐标。

3 考虑复杂气象变化的动态航线规划算法

3.1 海洋气象预报信息的获取与处理

本文用到的气象信息是从欧洲中期气象预报中心获取的。下载某一时刻全球风向、风速、波向和波高等分布数据，对其进行简单处理后导入仿真平台，用于估算船舶在该风浪条件下的航速。

3.2 动态航线规划算法设计

在完成气象信息导入后，就可以知道每个节点的风浪实况，鉴于此，在A*算法的价值函数中加入

天气影响因素。每个节点的气象实况不同，船舶航速受到的影响也不同，而且船舶在风浪较大的环境中失速情况严重，因此利用A*算法对路径进行规划，选取一条航行时间最短的路线，同时有效避开大风浪区域。本文提出的动态航线规划算法流程见图3。

在速度一定的情况下，距离与时间成正比，因此可以将价值函数中的代价值用时间代替，即从考虑路径最短转化为考虑用时最短，通过下式将优化目标转化为航行时间：

G（i）=Sm/vi （m=1，2）                              （9）

H（i）=G（i）

（xi-xG）2+（yi-yG）2（10）

式中：S1为2个水平或垂直相邻的节点之间的最短距离;S2为2个对角线相邻的节点之间的距离;

vi为船舶在节点i的航速。

在实际航行中，需要考虑天气对船舶航速的影响。从图4可以看出，在算法搜索当前节点周围的8个节点时，因为船舶在每个节点的航行方向不同，所以每个节点的相对风向和相对浪向也不同。以东北方向节点为例，

其相对风向为

δ=θ-φ，相对浪向为q=ρ-φ，这里θ为风的方向，ρ为浪的方向，φ为船舶航向。

将式（5）中v作为式（9）中的vi，即可得到考虑风、浪共同影响的从起点到当前节点i的G值。

应用刘烽[21]的计算公式在代价值G中加入风浪对失速的影响：

G（i）=Skv0-（a1h-a2qh+a3vWcos δ）（1-a4Dv0），

k=1，2（11）

应用上述规划方法，并将规划目标设定为从起点至目标点的航行时间，重新规划航线。图5中加入了大风浪区域，因为在计算代价值时考虑了风浪对航速的影响，所以算法会自动避开大风浪区域，选择风浪较小的路线。

4 智能船舶跨北大西洋的动态航线规划

根据上文提出的考虑复杂气象变化的动态航线规划算法，进行智能船舶动态航线规划软件的设计。

在Visual Studio编程平台上，运用C++编程读取电子海图数据和海洋气象数据，并实现风浪数据的可视化。选用北大西洋作为航线规划仿真的海域;采用的智能船舶的排水量为130 000 t，静水航速为20 kn;根据该船的主尺度参数，式（5）中系数的取值为

a1=1.08，a2=0.126，a3=0.002 77，a4=2.33×10-7。

4.1 考虑复杂气象变化的动态航线规划软件设计

在航线规划仿真前，需要分析电子海图数据结构，从海洋和陆地层数据中提取陆地、岛屿等多边形障碍物数据并导入仿真平台，通过比例尺换算和屏幕坐标转换绘制海图，然后取栅格精度为1°×1°对电子海图进行栅格化。根据多边形障碍物信息，可以将电子海图区域划分为可航行区域和不可航行区域。若栅格中心点位于多边形障碍物内部，则将栅格中心点定义为不可航行点;反之，則定义为可航行点。

T（A）=

0，A为可航行点

1，A为不可航行点

（11）

式中：A为任一栅格中心点。

利用几何图形判断法判断点A是否在多边形障碍物（下文简称多边形）内部。如图6所示，从点A水平引出一条直线与多边形相交。若点A的一侧与多边形的交点个数是奇数，则点A在多边形内部，否则点A在多边形外部。图6a中，点A左侧与多边形有3个交点，因此点A在多边形内部;图6b中，点A左侧与多边形有2个交点，因此点A在多边形外部。

根据上述方法完成海图静态障碍物建模。考虑风浪对船舶航线规划的影响，在可航行区域为风和浪建模。图7为海洋环境的模型，其中可航行区域分为3类：小风浪区域、中风浪区域和大风浪区域。由于风浪过大可能威胁船只安全，规划航线时需要绕开大风浪区域。

4.2 智能船舶动态航线规划与实验数据分析

在对海洋、陆地、风、浪建模的基础上进行智能船舶动态航线规划仿真。在海图上确定智能船舶的出发点和目标点。由图8左下角可知，智能船舶从出发点到目标点需要绕开陆地、岛屿等障碍物。本文在A*算法的启发式函数中加入风浪对船舶航速的影响，从图8能明显地看到航线随风浪变化发生了改变，所经过的区域风浪较小，有效地避开了大风浪区域。

在船舶航行过程中气象会随时间变化，甚至在短期内出现恶劣天气，因此在进行航线规划时需要依据实时的海上气象变化对航线进行相应的调

整。运用本文提出的动态航线规划方法，每隔一天

重新获取海上气象信息，并重新进行航线规划。图9为智能船舶航行3天后的航线规划结果。

为判断图9中规划出的航线是否为优质航线，对优化前航线、考虑风浪影响的优化后航线，以及通过动态规划得到的航线所需的航行时间进行估算，结果分别为206.99、175.56和169.38 h。

计算可知，

通过动态规划得到的航线的总航行时间比优化前航线的总航行时间减少了18.17%。从图8和9可以看出，大风浪区域随时间整体向右偏移，减少了绕航距离。

智能船舶跨北大西洋的航线规划仿真结果表明，本文提出的动态航线规划算法能够有效地优化海上航行路线，针对短期内出现的气象变化，实时调整当前航线，避开大风浪区域，减少智能船舶的总航行时间。

5 结 论

由于风浪对船舶航速有较大影响，本文提出一种考虑海上复杂气象变化的智能船舶动态航线规划方法。首先，通过分析电子海图的数据信息，将其中的地图数据转化成多边形坐标，导入仿真软件后对其进行栅格化。然后，提出一种几何图形判断法，判断每个栅格的中心点是否在多边形障碍物内部，并详细描述了地图建模过程，将电子海图分成可航行区域和不可航行区域，并利用海洋气象信息数据对风和浪进行建模。其次，在A*算法的启发式函数中加入风浪对船舶航速的影响，使得该算法能够根据气象的实时变化对船舶航线进行动态调整，让船舶能够在航行过程中避开大风浪区域。最后，进行智能船舶跨北大西洋的航线规划仿真，仿真结果表明：本文提出的动态规划算法不仅能够保障船舶有效避开大风浪区域，而且明显缩短了总航行时间。

参考文献：

[1]李小刚. 基于遗传算法的船舶气象航线设计方法的研究[D]. 长春： 吉林大学， 2018.

[2]冷教恒. 恶劣天气海况与船舶航行安全[C]//中国航海学会海洋船舶驾驶专业委员会.气象海洋环境与船舶航行安全论文集. 中国航海学会， 2010： 147-150.

[3]LARRSSONE， SIMONSEN M H， MAO Wengang. Direct optimization algorithm in weather routing of ships[C]//Proceeding of the 25th International Ocean and Polar Engineering Conference. Hawaii， USA： The International Society of Offshore and Polar Engineers， 2015.

[4]陆潇杨， 刘志全， 褚振忠. 漂角修正的欠驱动船舶航向鲁棒自适应控制[J]. 上海海事大学学报， 2020， 41（1）： 15-19. DOI： 10.13340/j.jsmu.2020.01.003.

[5]褚善东. 船舶在大风浪中航行产生的失速问题探讨[J]. 浙江国际海运职业技术学院学报， 2008， 4（2）： 1-3.

[6]ROHM. Determination of an economical shipping route considering the effects of sea state for lower fuel consumption[J]. International Journal of Naval Architecture and Ocean Engineering， 2013， 5（2）： 246-262. DOI： 10.2478/IJNAOE-2013-0130.

[7]LINY H， FANG M C， YEUNG R W. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements[J]. Applied Ocean Research， 2013， 43： 184-194. DOI： 10.1016/j.apor.2013.07.010.

[8]曹永恒. 基于粒子群優化算法的船舶航迹规划方法研究[D]. 上海： 复旦大学， 2010.

[9]SZLAPCZYNSKAJ. Multicriteria evolutionary weather routing algorithm in practice[J]. TransNav： International Journal on Marine Navigation and Safety of Sea Transportation， 2013， 7（1）： 61-65. DOI： 10.12716/1001.07.01.07.

[10]TSOUM C， CHENG H C. An ant colony algorithm for efficient ship routing[J]. Polish Maritime Research， 2013， 20（3）： 28-38. DOI： 10.2478/pomr-2013-0032.

[11]随博文， 黄志坚， 姜宝祥， 等. 基于深度Q网络的水面无人艇路径规划算法[J]. 上海海事大学学报， 2020， 41（3）： 1-5. DOI： 10.13340/j.jsmu.2020.03.001.

[12]申子豪. 基于A*算法的船舶气象航线设计方法的研究[D]. 长春： 吉林大学， 2018.

[13]SEND， PADHY C P. An approach for development of a ship routing algorithm for application in the North Indian Ocean region[J]. Applied OceanResearch， 2015， 50： 173-191. DOI： 10.1016/j.apor.2015.01.019.

[14]ZACCONER， OTTAVIANI E， FIGARI M，et al. Ship voyage optimization for safe and energy-efficient navigation： a dynamic programming approach[J].Ocean Engineering， 2018， 153： 215-224. DOI： 10.1016/j.oceaneng.2018.01.100.

[15]梅斌， 孙立成， 史国友， 等. 一种高纬度区域船舶偏航距离的高精度求解算法[J]. 上海海事大学学报， 2018， 39（4）： 75-81. DOI： 10.13340/j.jsmu.2018.04.013.

[16]陈智康， 刘佳， 王丹丹， 等. 改进Dijkstra机器人路径规划算法研究[J]. 天津职业技术师范大学学报， 2020， 30（3）： 30-35. DOI： 10.19573/j.issn2095-0926.202003005.

[17]潘明阳， 刘乙赛， 李琦， 等. 基于改进A*算法的内河水网航线规划及应用[J]. 上海海事大学学报， 2020， 41（1）： 40-45. DOI： 10.13340/j.jsmu.2020.01.007.

[18]秦操， 杨荣武. 复杂水域慎思型避碰轨迹规划[J]. 上海海事大学学报， 2020， 41（3）： 12-18. DOI： 10.13340/j.jsmu.2020.03.003.

[19]CAIY， WEN Y Q， WU L. Ship route design for avoiding heavy weather and sea conditions[J]. TransNav： International Journal on Marine Navigation and Safety of Sea Transportation， 2014， 8（4）： 551-556. DOI： 10.12716/1001.08.04.09.

[20]杨振忠， 刘世歧. 船舶在风浪中航行的失速计算[J]. 中国航海， 1990（2）： 35-40.

[21]刘烽. 船舶在风浪中航行失速问题的研究[J]. 大连海运学院学报， 1992， 18（4）： 347-351.

（编辑 赵勉）