滴水湖无人船测试场应急保障航道规划
白响恩 周俊杰 肖英杰 徐笑锋 戚玉玲 沈建华 徐元 任鸿翔 曾建峰

摘要:
针对滴水湖新建无人船测试场的应急保障问题,建立基于Maklink图论和Dijkstra算法的多终点航道规划模型。通过环境建模确定障碍物大小和位置;受PNPoly算法启发,引入剔除函数进行模型改进;利用Dijkstra算法在无向网络图中搜索从起点至终点的最短应急航道,并利用蚁群算法对最短应急航道集合进行优化。结果分析显示,最终规划的航道高效、安全,规划结果可以为滴水湖管理工作和无人船测试场应急保障提供参考。
关键词:
滴水湖; 无人船测试场; 应急保障; 航道规划; Maklink图论; Dijkstra算法
中图分类号: U612.1; U697.1
文献标志码: A
收稿日期: 2020-09-08
修回日期: 2020-11-22
基金项目:
国家自然科学基金(51909155);上海市科学技术委员会项目(14170501600)
作者简介:
白响恩(1984—),女,上海人,副教授,博士,研究方向为船舶交通管理,(E-mail)xebai@shmtu.edu.cn
Emergency support channel planning for unmanned ship
test site in Dishui Lake
BAI Xiangen1a,1b, ZHOU Junjie1a,1b, XIAO Yingjie1a,1b, XU Xiaofeng1a,1b,
QI Yuling1a,1b, SHEN Jianhua2, XU Yuan3, REN Hongxiang4, ZENG Jianfeng3
(1.a.Merchant Marine College; b.Engineering Research Center of Shipping Simulation, Ministry of Education,
Shanghai Maritime University, Shanghai 201306, China; 2.Shanghai Pilot Station, Shanghai 200080, China;
3.Shanghai Waterway Engineering Design and Consulting Co., Ltd., Shanghai 200120, China;
4.Navigation College, Dalian Maritime University, Dalian 116026, Liaoning, China)
Abstract:
In view of the problem of emergency support for the new built unmanned ship test site in Dishui Lake, a multi terminal channel planning model is established based on Maklink graph theory and Dijkstra algorithm. The size and location of obstacles are determined by environmental modeling. The model is improved by introducing the elimination function inspired by PNPoly algorithm. Dijkstra algorithm is used to search the shortest emergency channels from the starting point to the terminals in the undirected network diagram, and the ant colony algorithm is used to optimize the set of the shortest emergency channels. The analysis of the result shows that the final planned channel is of high efficiency and safety, and the planning result can provide reference for the management of Dishui Lake and the emergency support of the unmanned ship test site.
Key words:
Dishui Lake; unmanned ship test site; emergency support; channel planning; Maklink graph theory; Dijkstra algorithm
0 引 言
隨着近年来物联网、大数据、云计算、人工智能等新理念、新技术的发展,无人船开始兴起,船舶不断向智能化过渡。相较于陆地环境和空中环境,水域环境的限制条件更多、安全风险更大,因此对水域进行航道规划十分必要。水域环境尤其是具备一定观光旅游条件的湖区,具有自身的独特性,为保障观光旅游的安全和可持续发展,在航道规划中需要纳入应急保障因素。航道规划的本质是路径规划,其实现离不开算法的支持。这些算法根据其实现原理可分为非进化型算法(如A*算法、人工势场法、Floyd算法等)和进化型算法(如TS算法、粒子群算法、遗传算法等)两类[1]。
传统的路径规划模型的构建较少结合具体情况改进,所采用的算法比较单一,容易出现运算结果较差、易陷入局部最优的情况,对复杂环境、特殊环境中的路径规划不够有效。刘云翔等[2]通过实验比较了A*算法与Dijkstra算法的搜索速度和搜索效率,以及在障碍物较多情况下的搜索效果;仝佳璐等[3]为解决空中航班流的运行问题,采用改进的双向Dijkstra算法求解多条改航路径;朱小林等[4]在综合各项因素的基础上,针对海上应急救援系统中应急资源的决策问题建立了基于事件类型的应急物资和船舶分配模型;余梦珺等[5]选取海洋相关指标构建出环境威胁场,利用蚁群算法对各目标在不同救援时段具有不同权重的情况展开西北航道海上救援路径规划;谢新连等[6]根据海上施工水域的航道规划问题,建立了以航线总长度最短为目标函数、不可航行区域为约束条件的航线规划数学模型。
为处置无人船在滴水湖新建无人船测试场测试期间发生的失控、碰撞或泄漏,甚至燃爆等危险情况,需要在测试场周围设置多个应急保障点,以确保意外事件发生后应急救援迅速,因此规划的航道应该满足高效性、安全性和易管理性。本文根据滴水湖实际环境,将剔除函数引入Maklink图论中对环境模型进行改进;考虑滴水湖地理环境的独特
性、无人船测试场的影响及应急保障等因素,选取3个目标终点,利用Dijkstra算法进行多终点航道规划;结合蚁群算法
对规划的航道进行优化,为滴水湖管理工作和无人船测试场应急保障提供参考。
1 滴水湖无人船测试场现状
1.1 背景概况
滴水湖位于上海市浦东新区南汇新城镇,整个湖呈圆形,直径约2 660 m,湖中心建有水滴雕塑,岸边连接北岛、西岛和南岛。随着上海自贸试验区临港新片区的经济发展,滴水湖成为该地区的旅游中心,涉及游船、快艇等多種船舶航行活动。
“滴水湖无人船测试场项目”是由包括上海临港海洋高新技术产业发展有限公司在内的多家单位和组织共同参与的新兴项目,旨在建立多功能前沿性无人船测试场。为保障无人船测试期间的安全,需要根据无人船测试场的布局对可能的突发情况制定应急物资输送、应急救援实施的交通组织规划尤其是航道规划。目前滴水湖一号码头具备充足的配套资源和应急保障能力。
1.2 通航环境
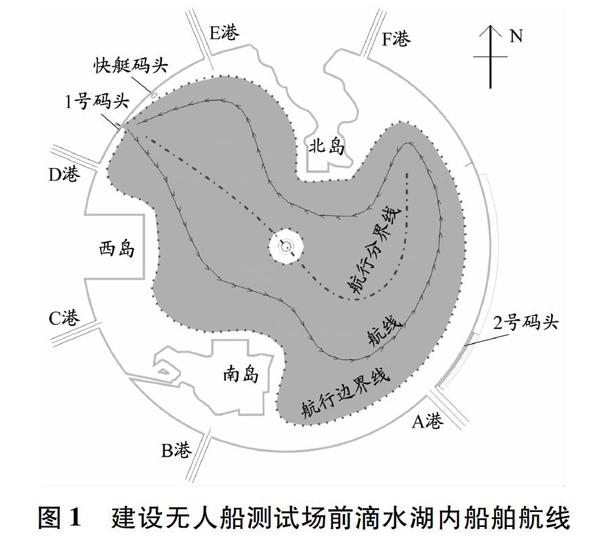
在建设无人船测试场前,滴水湖主要营运的船舶基本按照固定航线逆时针方向航行(见图1),没有一条真正意义上规范的航道。
无规范航道的现状及无人船测试场的介入,势必会对滴水湖内通航环境造成很大影响。无人船在
滴水湖进行测试时会占据很大一片水域,湖内其他船舶活动水域将大幅缩减,因此应急保障航道规划应考虑这些实际情况,以确保应急保障的快速、及时以及通航安全。
1.3 问题描述
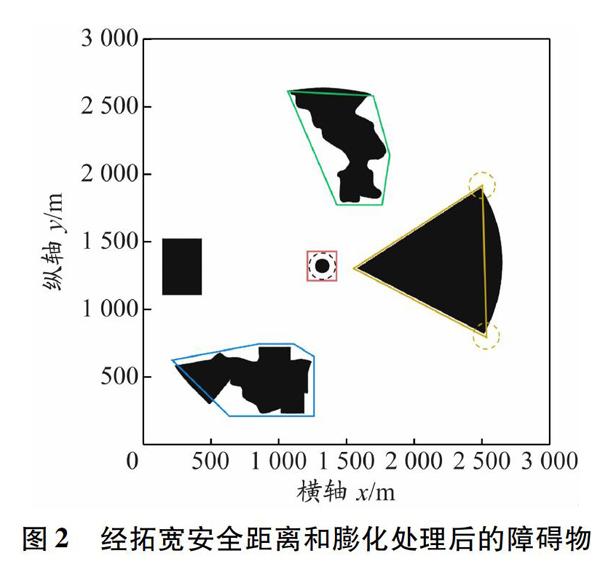
船舶在滴水湖内航行时会经过在建的无人船测试场(见图2中的扇形区域,其在建设完成前被定
义为施工障碍物,在建设完成后则被定义为一般障碍物)以及中心雕塑、北岛、西岛和南岛等4个静态障碍物。应急保障船舶在水域内航行应避开这些障碍物,同时为保证应急保障的全面性和及时性,需要根据无人船测试场地理位置为应急保障船舶设置多个终点。本文结合相关图论和算法设计出应急保障船舶从起点到多个终点的多条合理路径,实现滴水湖无人船测试场应急保障航道规划。
所有障碍物区域均需拓宽安全距离[7]。由于中心雕塑位于滴水湖正中位置,无论如何规划应急保障船舶均需经过此处,所以中心雕塑对航道影响较大;无人船测试场作为应急保障区域,在终点的数量和位置选取上要仔细斟酌。针对该情况,在中心雕塑处将安全距离拓宽60 m;把以无人船测试场外侧的两个端点为圆心、半径为100 m的两个圆形区
域作为终点选址区域(见图2中虚线圆);其余障碍
物处适当拓宽安全距离。
最终选取1个起点S和3个终点T1、T2和T3。
2 应急航道规划总体流程
基于Maklink图论和Dijkstra算法进行应急保障航道规划,需要结合滴水湖的独特环境进行合理、有效的创新,使规划出的航道安全且易于管理。应急保障航道规划主要包括坐标系的绘制、障碍物的膨化处理、二维路径规划模型的建立与改进以及算法的实现,具体流程见图3。
3 环境模型
3.1 环境建模
由于滴水湖内船舶所处位置海拔高度基本相同,所以环境模型建为二维模型。环境建模基于Maklink图论[8-9],考虑到其复杂性并涉及多图展
示,作如下说明:①环境模型规格为3 000 m×
3 000 m。②自由链接线(采用虚线段表示)被定义为两个障碍物之间不与障碍物相交的端点之间的连
线,以及障碍物端点到环境模型边界线的垂直线段;省略个别邻近的不具显著实际效果的自由链接线;vi表示自由链接线
Li的中点
(以下简称“节点”),i∈N*。③障碍物并非全部为规则形状,如北岛、南岛均为极不规则形状,中心雕塑为圆形形状,无人船测试场为近似扇形形状。这类障碍物需要进行“膨化处理”[10],膨化处理后的障碍物由凸多边形替代。④可行路径(采用实线段表示)为每两个节点有效相连的结果,其中“有效”指线段不可与其端点外的虚线线段相交,且线段不可穿越障碍物。经拓宽安全距离和膨化处理后的障碍物见图2。
构建出的滴水湖无人船测试场的具体环境模型无向网络图见图4。
3.2 模型改进
基于Maklink图论构建的滴水湖无人船测试场环境模型,能够完整包含在3 000 m×3 000 m的范围内。所规划出的应急航道不能超出滴水湖水域,因此需要将环境模型进行改进。
受PNPoly算法启发,构造剔除函数,对环境模型进行改进。
对待测点vi的坐标(xvi, yvi)与多边形顶点坐标(设任一顶点e的坐标(xe, ye),与e相邻的另一个顶点r的坐标(xr, yr))进行相关运算,判断vi是否处于多边形内部,核心公式为
xvi<(xr-xe)(yvi-ye)yr-ye+xe
如果上式成立,则节点vi位于多边形顶点e与r之间边的左侧。依次对节点vi与多边形其他边的关系进行判断,若该节点位于多边形边的左侧的情况总共有偶数次,则保留该节点,否则剔除该节点。
将PNPoly算法与Maklink图论结合,并根据滴水湖的具体情况对环境模型进行改进,将环境模型从“多边形”改为“圆形”,进一步进行筛选。先在模型中给出直径为2 660 m的圆形界限,圆心坐标为(1 330,1 330)m,与纵轴和横轴分别相切于(0,1 330)m和(1 330,0)m;再将所有节点组成一个节点集合V;然后引入剔除函数f(vj),保留界限内的节点,剔除界限外的节点;最后对变化后的自由链接线进行处理。剔除函数构造流程见图5。
f(vj)=1, (xvj-xo)2+(yvj-yo)2≤1 3302
0, (xvj-xo)2+(yvj-yo)2>1 3302
式中:o表示圆心。
如图6所示,给出圆形界限后,无效的自由链接线和节点均被剔除,Maklink图中保留的自由链接线和节点在该界限内,环境模型改进后较改进前更简洁明了,保证了模型符合实际,也将有助于改善后续应急保障航道规划的效率。环境模型改进结果见表1。
4 Dijkstra算法航道规划
4.1 Dijkstra算法介紹
Dijkstra算法[11]是一种单源路径算法,也是一种贪心算法,它以起始点为中心向外层层扩展直至终点,用来求解一个顶点到其余各顶点的最短路径问题。Dijkstra算法十分简洁,能够有效地找到最优解。基于Dijkstra路径规划的优势,对滴水湖应急保障航道进行规划。在图6的无向网络内从起点
到终点进行路径规划,Dijkstra算法实现步骤[12]如下:
步骤1 对未确定最短路径的节点集合Vk和已确定最短路径的节点集合V′k进行初始化操作(其中k为迭代次数),根据无向网络图的可行路径计算各节点间的距离,同时建立带权图的邻接矩阵M,相邻节点间的权值即为距离对应数值
,不相邻节点间的权值赋值为∞,从起点S到相应节点的最短路径长度用数组D表示。
步骤2 选择数组D中的最小值Di,将Di对应的节点vi从集合Vk中取出,存入集合
V′k内。
步骤3 根据节点vi修改更新Di中从起点S到集合Vk中其余节点的路径长度。
步骤4 循环步骤2和步骤3的操作,重复迭代,直至寻找出从起点S到无向网络图中所有节点的最短路径为止,并最终到达终点T。
4.2 应急保障航道规划
假设用Dijkstra算法规划出的最短路径经过d个节点(起点和终点除外),
用
p(0)m和p(1)m分别表示以原点为起点、Lm(m=1,2,…,d)的两个端点
为终点的向量,则Lm上其他点的表示方法为
式中:pm(χm)表示以原点为起点、Lm上任意一点为终点的向量;χm为0与1之间的随机数,表示自由链接线比例参数。
求解数组D和矩阵M均需要知道各节点vi的坐标,vi的坐标应根据各障碍物端点坐标进行计算,端点坐标测量通过
AutoCAD 2020实现。利用Dijkstra算法得到从起点S至终点T1、T2和T3的3个22×
22阶的邻接矩阵M1、M2和M3:
Dijkstra算法求解通过MATLAB R2016a实现。得到的多终点应急保障航道规划结果(见图7)分别为:S→v4→v5→v6→v9→v10→v18→v20→T1,距离为3 319.65m;S→v4→v8→v14→v13→v12→v11→T2,距离为2 829.27m;S→v4→v8→v14→T3,距离为1 696.09m。
5 蚁群算法航道优化
5.1 优化原理
蚁群算法是一种新型进化算法,通过模拟蚂蚁的行为规律(蚂蚁在走过的路径上会释放一种信息素,后面的蚂蚁会优先选择信息素浓度较高的路径),根据正反馈机制寻找出最优的路径[13]。采用蚁群算法时需要离散化工作空间,由于最初选择的自由链接线长短不一,需要采用固定距离划分法。假设
ζ为划分出的每段短线段的长度,每条自由链接线Lm的划分段数为
Qm=int(Lm/ζ),int(Lm/ζ)为偶数
int(Lm/ζ)+1,int(Lm/ζ)为奇数
式中:当int(Lm/ζ)为奇数时,因为路径中点也是一个等分点,所以划分段数需加1。经过离散处理后,从自由链接线Lm-1到其相邻的自由链接线Lm将有Qm+1条路径可以选择。
通过Dijkstra算法求得路径后,只要给定一组参数(χ1,χ2,…,χd),就可以得到一条从起点到终点的新蚁群算法路径。
设定q0为蚂蚁对信息素感知的阈值(q0∈[0,1]),q为[0,1]内的
一个随机数,某只蚂蚁在Lm+1上未走过的等分点集合为A,h∈A。当该蚂蚁到达Lm上某个等分点g时,采用轮盘赌法选择Lm+1上的等分点:当q≤q0时,以

