纵横波波场分离效果对比
郭政宏,胡叶正
(西南石油大学 地球科学与技术学院,四川成都 610500)
弹性波正演是认识地下复杂介质的重要手段,在弹性波有限差分正演模拟中,除了二阶质点位移方程外,常用一阶速度-应力方程,其优点是不需要对弹性参数进行空间微分,就可以得到完整的地震波场响应[1]。除了常规网格外,Madariaga提出的交错网格,它在不增加计算量的前提下,和常规网格相比局部精度提高了4倍,收敛速度也很快,很好地压制了数值频散[2]。
弹性波纵横波场分离是进行弹性波逆时偏移的必要条件,如若不能正确分离纵横波场,则在偏移成像过程中由于纵横波的互相干扰,导致偏移成像失败。目前大多数学者都采用传统的Helmholtz原理分离纵横波场。Helmholtz分解基于弹性波混合波场是由一个无旋场和无散场组成的,这个无旋场就是纵波的势函数,无散场就是横波的势函数。因此可以通过对混合波场做散度运算提取纵波,做旋度运算。但是由于旋度运算和散度运算对空间做了一阶偏导数,分离后的波场的振幅和相位都会改变,且分离后的纵横波波场与原波场的物理意义不一致。假设原波场为位移,那么经过Helmholtz分离后的波场为质点速度相关的一个量。而且对其做相位矫正和振幅恢复时计算量过大,对后期的逆时偏移来算不易实现。本文采用纵横波解耦方程有限差分交错网格形式下的正演模拟,吸收边界采用CPML。在提高计算效率上利用MPI和OpenMP进行并行加速。
1 基本原理与方法
1.1 弹性波各向同性一阶速度-应力方程
密度非均匀,二维弹性波各向同性一阶速度-应力方程:
式(1)中:vx、vz为弹性波质点振动速度的水平分量和垂直分量(在多波多分量地震勘探中,也被称之为伪横波和伪纵波);τxx、τzz、τxz为质点振动x轴向,z轴向的正应力,和y平面法向的剪切应力;λ、μ则为弹性波的模量,其中μ是剪切模量;ρ表示为密度参数。
其中,密度,纵横波速度参数和弹性波的模量参数关系如下:

弹性波一阶速度-应力方程交错网格各个分量的配置方式如图1所示,其中密度位于半网格点上。
各向同性弹性波介质中,纵波和横波是完全解耦:纵波是一个有源无旋散度场,横波是一个有旋无散的散度场,混合波场是由一个散度场(纵波波场)和一个旋度场(横波波场)叠加而成。
基于Helmholtz弹性波纵横波场分离理论,可以从质点振动速度的水平分量和垂直分量提取散度获得纵波波场,从中提取旋度获得横波波场。
时空域直接采用散度算子和旋度算子如下:

从式(3)中可以看出,Helmholtz分离后的纵横波场,其相位整体移动了90°,纵横波振幅比也发生了变化,同时得到的纵横波波场和原波场的物理意义也不相同。
1.2 纵横波解耦的一阶速度-应力方程
密度非均匀,各向同性纵横波波场分离方程:
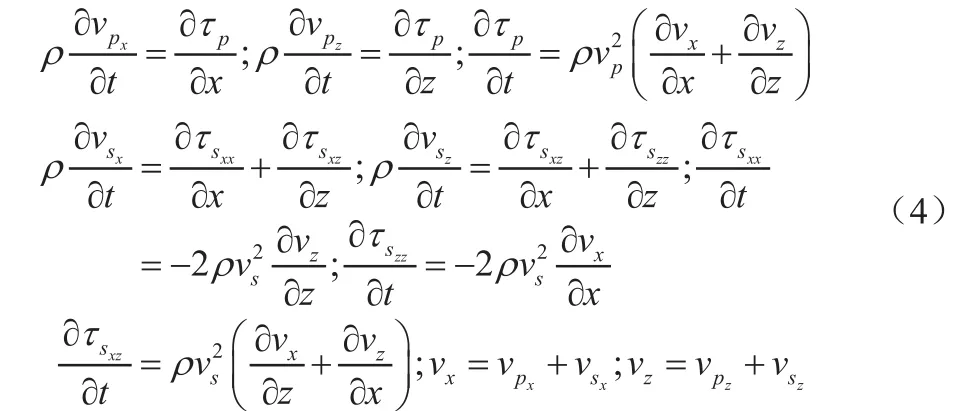
应用有限差分进行弹性波波动方程正演时,由于正演的空间有限,需要在节段的人工边界上引入吸收边界条件。当前吸收效果较好的边界条件是完全匹配层(PML)边界,它能够使大角度入射的弹性波在匹配层中无反射地通过,并按照指数规律进行衰减。由于在弹性波正演模拟中,纵波速度、横波速度和密度的差异变化复杂,使用常规的PML吸收边界会留下一些反射波和大量的隐失波,而采用CPML算法后则可以大大减少反射波的存在,并且对隐失波的吸收具有很好的效果。
2 模型测试
选取Mamousi模型的一块区域(图1(a)),该区域的网格大小为(1 201×401),空间采样间隔为5m,纵横波波速比为1.73,不考虑密度模型(密度默认为1),纵波震源激发,零相位雷克子波,震源主频30Hz,时间采样间隔0.000 5s,有限差分阶数16阶,CPML吸收层数32。

图1 速度模型及波场分离
基于弹性波各向同性一阶速度-应力方程,并采用Helmholtz原理提取的纵横波场如图1所示。使用相同正演模拟参数,基于纵横波解耦一阶速度-应力弹性波方程分离的纵横波如1(b)所示。
由于采用弹性波进行正演模拟,正演记录中出现了特有的面波现象,这是由于纵横波或者部分分量耦合在一起导致的,是声波正演模拟所不具有的特征。由于Marmousi的模型相对复杂,其反射波比较杂乱,波场也相对复杂。
对比图1(b)和图2(a),分离出的纵横波振幅与图1(a)相比更加符合真实的纵横波振幅比值,其反射波的细节更加清晰。同时纵横波解耦分离的纵横波保持原有的矢量特征,这与通过Helmholtz分离出来的标量波场有本质不同,分离出来的波场的物理意义和原来的波场的物理意义相一致。
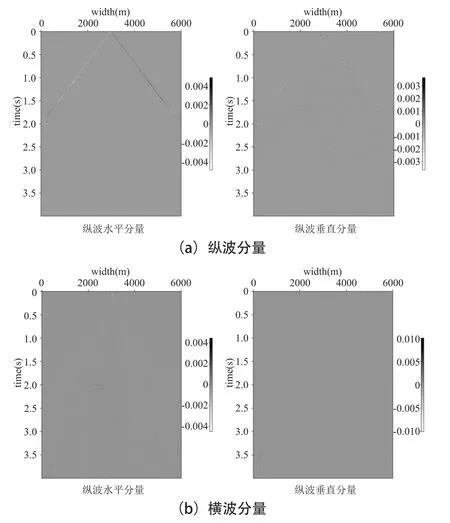
图2 纵横波解耦
3 结论
基于纵横波解耦方程交错网格下进行数值模拟,并借助Marmousi模型进行测试。同时和基于Helmholtz纵横波分解的方程相比,前者提取到纵横波场振幅和相位没有发生变换,波场的细节清楚,其分离出的波场干净,更加适应于后续的弹性波逆时偏移成像等工作流程。

