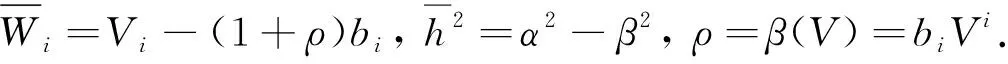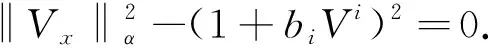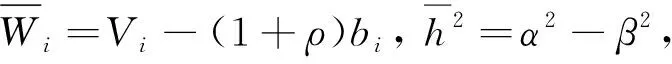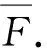黎曼流形上导航术问题的推广
程新跃,瞿秋红
重庆师范大学 数学科学学院, 重庆 401331
众所周知, 求解Zermelo导航术问题一直是探索和研究芬斯勒空间结构的重要方法之一, 对推进芬斯勒几何的研究发挥了重要作用. Zermelo导航术问题是考虑度量空间中的一个运动物体在内力和外力的作用下从一个点运动到另一个点所走的最短时间路径问题[1-2]. 文献[1]在芬斯勒空间上推广了Zermelo导航术问题, 证明了在芬斯勒流形(M,F)上, 在满足F(x, -Wx)<1 的外力场W的影响下, 最短时间路径是由方程
(1)
(2)
得到的解为
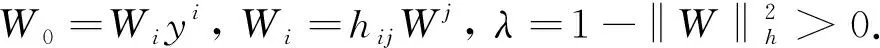

(3)
此时,F是Kropina度量. 由(3)式确定的度量F在切丛TM上并不是正则的, 但在锥形区域A=∪x∈MAx上是正则的, 这里
(4)
我们称这样的度量为锥Kropina度量. 如果令
(5)
则由(3)式确定的Kropina度量F也可等价地表示为
此时,F仍然在锥形区域A=∪x∈MAx上是正则的, 且Ax可表示为
(6)
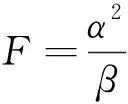
从本质上讲, 芬斯勒流形上的Zermelo导航术问题与流形的单位切球的几何有着密切的关系. 事实上, 芬斯勒流形上的导航术问题总对应于单位切球沿一个给定向量场的平移. 具体地, 在芬斯勒流形(M,Φ)上, 任意点x∈M处的单位切球SΦ是切空间TxM在原点x附近的一个封闭超曲面,SΦ={y∈TxM:Φ(x,y)=1}. 假定V=V(x)是流形M上的一个向量场, 并且Φ(x, -Vx)≤1, 考虑SΦ沿向量场V的平行移动SΦ+{V}. 易知y∈SΦ+{V}当且仅当Φ(x,y-Vx)=1, 即在切空间TxM上,SΦ+{V}的方程为Φ(x,y-Vx)=1. 进一步, 我们有以下两个重要的观察结果:
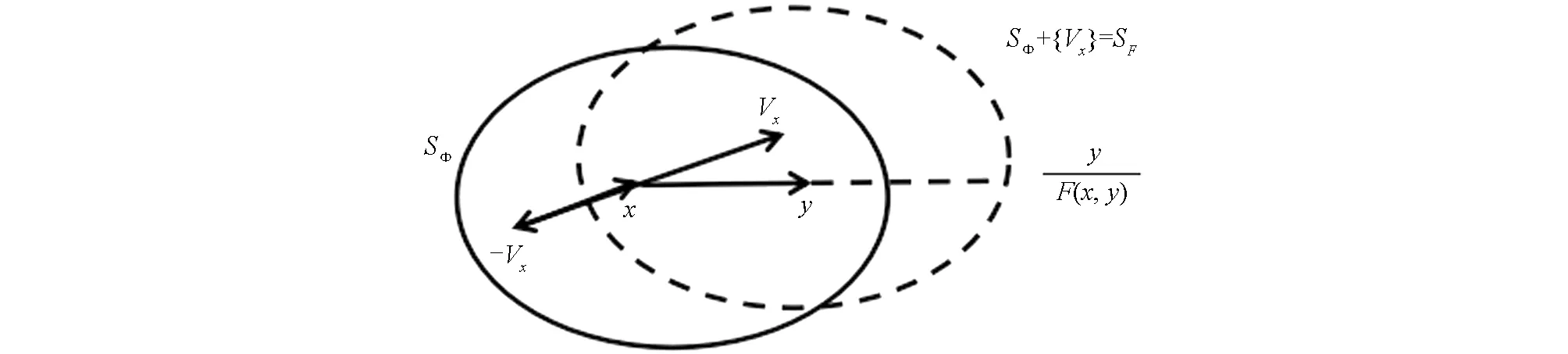
图1 Φ(x, Vx)<1时的图SΦ+{V}
在这种情况下, 易见对于任意的y∈TxM-{0}, 一定存在唯一正数F=F(x,y)>0, 使得
(7)
这等价于F(x,y)满足
(8)
可以证明, 这样的F=F(x,y)是正则的芬斯勒度量[3]. 显然, 由(8)式可知F是由导航数据(Φ,V)确定的导航术问题的解.
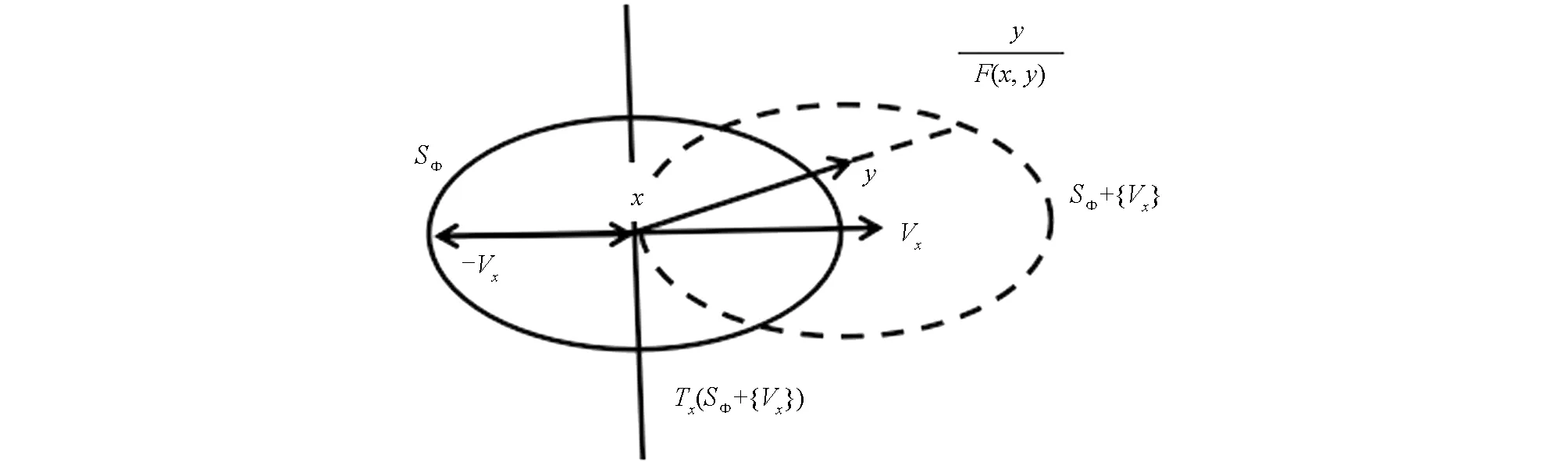
图2 Φ(x, -Vx)=1时的图SΦ+{V}
在这种情况下, 易见对于任意的y∈Ax={y∈TxM:gV(y,Vx)>0}, 存在唯一正数F=F(x,y)>0, 使得F=F(x,y)满足(7)式, 亦即等价地满足(8)式. 此时,F=F(x,y)是锥芬斯勒度量.
上述观察对深刻认识导航术技巧的几何本质, 深入推进利用导航术技巧来揭示芬斯勒空间的几何性质与结构的工作是极为重要的.
1 预备知识
在这一节中, 我们简要介绍关于Randers度量及Kropina度量的知识.
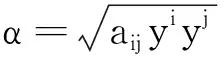
的度量, 这里φ=φ(s)是定义在(-b0,b0)上的正的光滑函数, 且满足
φ(s)-sφ′(s)+(b2-s2)φ″(s)>0 |s|≤b 本文着重讨论和研究正则的Kropina度量, 把Kropina度量定义在切丛的锥形区域A=∪x∈MAx上, 其中 (9) 即 (10) 把(10)式化简后得 进一步, 有 (11) (12) 其中ρ=V(b)=biVi. 整理后, 有 (13) (14) (15) (16) 利用文献[2]中的引理1.1.1, 可得 (17) 由此可得 (18) 定理2设F=α+β是n维流形M上的Randers度量,V是流形(M,F)上的向量场且满足F(x, -Vx)=1. 则由导航数据(F,V) 确定的导航术问题的解为 (19) 把(19)式化简后得 (20) (21) 由(21)式易得 (22)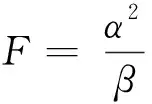
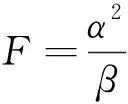
2 Kropina流形上的导航术问题

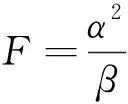
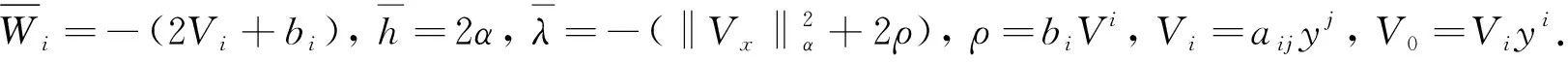
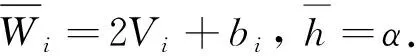


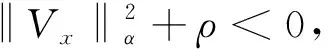

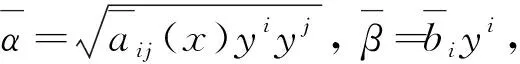
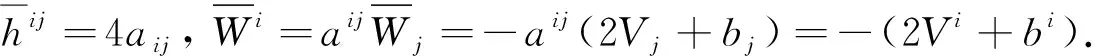

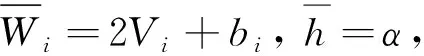
3 Randers流形上的导航术问题