面向车联网的多智能体强化学习边云协同卸载
叶佩文,贾向东,杨小蓉,牛春雨
(1.西北师范大学计算机科学与工程学院,兰州 730070;2.南京邮电大学江苏省无线通信重点实验室,南京 214215)
0 概述
目前,车辆消费升级、道路容量日趋饱和等客观因素加剧了城市的交通困境。在5G 商用落地同时展望6G 愿景的背景下,构筑“车-人-路-云”泛在连接的车联网(Internet of Vehicles,IoV)成为必然趋势[1-2]。与此同时,在城市中部署智能交通系统(Intelligent Transportation System,ITS)缓解交通压力也已成为主流选择。而车联网作为ITS 的核心部分,更需要在网络架构和使能技术上不断演进[3]。
在网络架构方面,得益于云计算技术的迅猛发展,车联网的大量计算任务可以有效地迁移到分布式云端服务器上进行数据处理、统一调度和计算资源分配。然而,单一的车辆云架构不可避免地要求数据进行长距离、高时延传输,这无法满足需要敏捷响应的V2V 安全类信息通信要求。通过分析车辆行为与预测模型可以发现车辆群体存在局部性特征[4-5],即计算任务的卸载范围通常局限于相邻行驶车辆或车与周边路旁单元之间,而将移动边缘计算(Mobile Edge Computing,MEC)作为一种新的范式引入车联网,能够将计算能力下沉至网络边缘,从而减少服务时延[6]。
在使能技术上,车联网边缘计算卸载可利用凸优化、图论以及博弈均衡等方法。但近年来人工智能特别是深度强化学习[7-8]在计算机视觉、自然语言处理、语音识别等领域获得巨大成功,这吸引了国内外学者重新思考车联网边缘计算卸载方案的设计思路。
现有车联网边缘卸载策略存在场景同质化严重的问题,且在性能上仍有较大的提升空间。本文针对更泛在的城市街道场景,结合强化学习和随机几何理论,提出一种边云协同的车辆边缘卸载方案。结合随机几何理论和人工智能方法优化车联网边云卸载过程,将每个源车辆单元(Source Vehicle Unit,SVU)作为智能体来进行学习决策,并把由此产生的复杂训练过程转换到云端训练神经网络中,使SVU 仅依靠局部决策即能把握全局特征。此外,还将资源队列模型作为神经网络输入前件,以降低维灾风险。
1 相关工作
文献[9]针对车辆边缘计算(Vehicular Edge Computing,VEC)网络提出了移动感知的任务卸载方法,以达到执行成本最小化的目的。文献[10]提出一种联合云计算、移动边缘计算和本地计算的多平台智能卸载方案,根据任务属性,利用强化学习算法选择卸载平台,旨在最小化时延并节省系统总成本,但网络模型中的控制面和数据面深度耦合,使得任务处理缺乏灵活性。文献[11]提出了基于软件定义[12]的车载网络框架,其核心思想是将控制面和数据面分离,使运营商能够更灵活地控制和更快速地部署网络,但是车辆业务复杂和网络拓扑结构多变的因素导致这一框架对车辆特征的抽象还不够成熟,相应的车载网络虚拟化技术仍需要深入研究。文献[13]针对类似高速路口拥塞场景,利用车联网异构资源性能互补特性,即计算资源开销来供给通信资源需求,提出了基于雾计算[14]的车联网边缘资源融合机制,从而弥补车联网资源时空分布不均的不足,但雾化机制[15]涉及大量基础设施的改造和升级,因此,该机制在构建部署阶段仍面临诸多挑战。
文献[16]针对车联网超可靠低延时通信(Ultra-Reliable Low-Latency Communication,URLLC)过程,将有异构性需求的车辆节点作为多智能体,利用强化学习进行数据卸载决策。文献[17]以相邻的车辆节点作为移动边缘服务器,以路边设施作为固定边缘服务器,利用半马尔科夫过程对时变信道进行建模,使移动用户根据Q 学习算法确定卸载对象,同时针对增加训练过程动作状态空间可能引起维灾的问题,提出利用深度神经网络来逼近Q 函数的深度强化学习算法,旨在使系统总效用最大。文献[18]基于值迭代和策略迭代两种思路提出动作-评价学习(Actor-Critic learning,AC)算法。得益于Actor 执行动作然后Critic 进行评估的优势,该算法在高维度空间仍具有良好的收敛属性,但存在评价策略偏差较大的问题,导致求解所得只是局部最优解。文献[19]将无线信道状态、缓存状态以及计算能力均纳入系统状态作为环境进行交互,由于通信、缓存、计算(Communication,Caching,Computing,3C)资源在应用场景具有耦合互补的特性,因此综合权衡3C 资源效用为任务调度卸载提供了一个广阔的思路。文献[20]在此基础上进一步考虑了时间尺度对协调优化的影响,提出大时间尺度采用粒子群优化理论而小时间尺度采用深度Q 学习算法调优的细化方案。
然而,现有车联网边缘计算方法普遍存在以下不足:1)多数方法仅在单一的高速公路场景进行建模,而此类场景通常假定车辆服从空间泊松过程(Spatial Poisson Process,SPP),这明显限制了适用范围,且简化了车联网实际通信的真实时空分布;2)云计算平台大多采用集中式部署方案,计算任务从本地迁移到云端存在重构开销,且队列形式的任务传输易导致额外排队时延和无序争用,而目前缺乏边缘计算节点协同云平台的相关研究;3)在利用人工智能手段方面,现有研究的奖励机制设计单一,从而导致训练模型的泛化性较差。
本文结合强化学习和随机几何理论,提出一种边云协同的车辆边缘卸载方案,主要包括以下工作:
1)针对场景趋同、系统建模局限的问题,将城市街道建模为经典Manhattan模型[21],并利用随机CoX过程[22]对移动车辆进行细粒度建模,相应考虑视距(Line of Sight,LoS)和非视距(Non-Line of Sight,NLoS)两种情况的信道状态。进一步地,考虑到级联对象包含目标车辆单元(Target Vehicle Unit,TVU)和路边单元(Rode Side Unit,RSU),对于SVU 而言在时空上具备离散性和流动性,通过随机几何理论分析级联对象接收信干比(Signal to Interference Ratio,SIR)覆盖概率,从而划分出卸载节点的优先级,从根本上消除转化成组合优化问题的必要性,降低计算复杂度。
2)依据边云协同的思想,将SVU 作为智能体进行决策,并将决策记录作为经验上传到云端,云端通过经验训练神经网络,每隔一段时间将训练更完备的神经网络反馈到边缘节点上。由此,只专注局部决策的SVU 能够捕捉到云端存储的全局特征而无需承担复杂的训练过程。
3)由于强化学习的本质是环境交互和基于奖励,因此设计更贴近实际的多角色博弈奖励机制。同时,为使从全局观察缩小到局部观察具有实质性作用,将节点资源队列分析作为输入的预先工作,从而减少计算任务的排队时间,并在一定程度上降低维灾风险。
2 系统模型
本文研究的系统模型如图1 所示,其中小区的网络架构由基站(Base Station,BS)和RSU 共同组成。基站通过核心网络连接云端服务器,具有计算能力的RSU作为固定边缘服务器(Fixed Edge Server,FES),中央云服务器可以通过回程链路连接FES 支持远程调度。将具有计算能力的TVU作为移动边缘服务器(Mobile Edge Server,VES),并从更广义的角度定义边缘节点性质,包括TVU 和RSU 两种类型。

图1 车联网边云协同卸载系统模型Fig.1 System model of collaborative edge and cloud offloading for IoV
假设本地计算容量已饱和,上述场景下的卸载途径可分为以下3 种情况:1)在LoS 范围内,SVU 将计算任务卸载给相邻满足条件的TVU,由于车辆到BS 上行链路的利用相对不充分,且BS 端对干扰更具可控性,因此为提高频谱利用率,SVU 可以复用V2B 上行链路进行计算任务卸载;2)在NLoS 范围内,SVU 同样可以复用V2B 上行链路进行计算任务卸载;3)在基础设施完备(即已部署RSU)的车辆稀疏路况场景中,SVU 可以将计算任务卸载到满足条件的RSU 端。
本文将车联网的空间分布建模为泊松线性Cox 点过程(Poisson Line Cox Point Process,PLCPP),对象包含车辆节点和路边节点。具体过程如下:将车辆节点空间分布建模为密度为μV的独立PLCPP,用ΦV表示;考虑到RSU 沿道路布放,将RSU 空间分布建模为线密度为μR的独立泊松线过程(Poisson Line Process,PLP),用ΦR表示。假设车辆节点中TVU 占比为β,遵循PLCPP,则TVU 服从密度为μTVU=μVβ的PLCPP,SVU服从密度为μSVU=μV(1-β)的PLCPP。
2.1 通信模型
不失一般性,本文假设SVU 使用最近距离级联卸载准则[23],并遵循广义边缘节点性质。定义计算任务集合T={T1,T2,…,TJ},SVU 集合用K表示,TVU 集合用N表示,RVU 集合用ϒ表示。考虑计算任务卸载到边缘节点存在视距(LoS)和非视距(NLoS)两种情况,在周期t内,SVU 卸载计算任务Tj(j∈J)到边缘节点的路径损耗可表示为:

因此,LoS 范围内卸载到第k个TVU 的频谱效率可表示为:

引理1假设SVU 的卸载许可半径为LS,与SVU级联的TVU接收的SIR覆盖概率可表示为式(4),其中,。证明见文献[23]。

结合式(2)~式(4)可知,从第k个SVU 卸载到第n个TVU 的数据速率为:

类似地,对于SVU 处于车辆稀疏且RSU 设施完善的区域,SVU 可以卸载计算任务到满足条件的RSU,与第k个SVU 级联的第r个TVU 接收的SIR 为:

其中,I(k)TVU是来自TVU 的干扰,I(k)r′是来自其他TVU的干扰。
因此,卸载到第r个RSU 的频谱效率可表示为:

引理2假设SVU 的卸载许可半径为LS,与SVU 级联的RSU 接收SIR 覆盖概率可表示为:

结合式(7)和式(8)可知,从第k个SVU 卸载到第r个RSU 的数据速率为:

2.2 计算模型
在计算卸载过程中,可定义SVU 的卸载任务Tj≜(Hj,Qj,),其中,Hj表示计算任务数据大小,Qj表示完成任务所需计算资源量,表示最大等待时间。
对于将计算任务卸载到TVU 的场景,SVU 卸载计算任务Hj到TVU 的时间开销包括通信时间和计算时间两部分。
卸载到TVU 的通信时间取决于计算任务数据大小Hj和提供服务TVU 的数据速率,结合式(9),通信时间可以表示为:

对于卸载到TVU 的计算任务,依照队列形式保存到TVU 缓存中,并更新资源队列状态,实行任务迁移,保证排队延时远小于任务计算时间。因此,计算时间仅依赖于任务所需计算资源Qj和TVU 的计算能力fTVUj(即单位时间内CPU 周期数),可表示为:

结合式(10)和式(11)可知,TVU 的总执行时间为:

类似地,将计算任务卸载到RSU 场景的执行时间同样包括通信时间和计算时间两部分。
卸载到RSU 的通信时间可表示为:

卸载到RSU 的计算时间可表示为:

结合式(13)和式(14)可知,RSU 的总执行时间为:

2.3 资源队列分析模型
SVU 在卸载计算任务时需要考虑卸载节点计算队列大小。不失一般性,假设队列节点初始资源量为qinitial,平均计算任务到达率E[Tj]=λ,在许可半径LS内满足资源量的TVU 和RSU 概率分别可表示为:
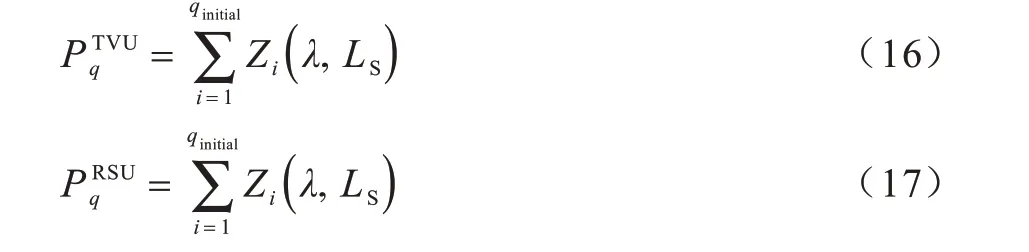
其中,Zi(λ,LS)表示Zipf 分布。
假设所考虑的车联网中SVU在周期t内生成任务的概率为pj,SVU级联卸载节点可提供的资源量表示为Θ=P(D2)(1-pj)μTVUμSVUE[L],其中,P(D2)表示平面周长,E[L]表示道路平均长度。因此,TVU所需保证的队列长度为ΘTVU=Θ(1-PTVUq),SVU所需保证的队列长度为ΘSVU=。相应地,对于周期t内生成任务Tj,卸载节点资源队列长度。
3 问题描述
本节分别从执行时延、能耗约束和费用开销维度分析车联网任务卸载问题,并量化统一成系统效用评价卸载性能,将3 个维度评价性能的累加作为奖励机制来反馈训练神经网络。
1)执行时延。定义F 为指示符,用于区分TVU 和RSU,则计算任务Tj执行时延可表示为:

3)费用开销。考虑实际网络架构包括车联网运营商(Vehicle Network Operator,VNO)、基础设施供应商(Infrastructure Provider,InP)和业务供应商(Service Provider,SP)三类角色。假设VNO 需向InP 支付的频谱租赁费用为ε,VNO 需向SP 支付计算费用φ,则计算任务Tj的费用开销包含通信开销和计算开销两部分,可以表示为:
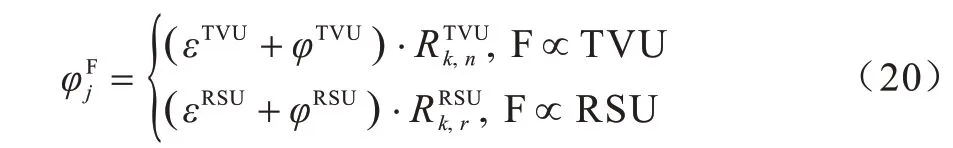
综上所述,基于多角色博弈的奖励机制,卸载任务的系统效用可由执行时延、能耗约束和费用开销三者的子效用累计和来表示,即:

其中,ω=[ω1,ω2,ω3]表示子效用系数,在训练过程中通过调整该参数来确定子效用的倾向性,例如在稀疏场景下更关注费用开销,而在密集场景下更关注执行时延。
4 多智能体强化学习边云卸载机制
车联网是典型的高速移动实时传输场景,在其中进行单一云端集中式优化存在参数冗余、更新滞后和耗费通信开销等问题。分布式边云协同机制利用云端将训练更完备的神经网络反馈到边缘节点,使得边缘节点仅需要相邻节点信息来更新参数执行操作。本节首先介绍状态空间、动作空间及系统效用,然后描述多智能体强化学习流程及改进方案。
1)状态空间。用S表示状态集合,在时刻t的状态可表示为,该状态表征了计算任务Tj的时延、能耗和开销状态。
2)动作空间。定义动作集为A,计算任务采取的动作αj∈A,αj=1 代表计算任务Tj卸载到TVU 上执行,αj=0 代表计算任务Tj卸载到RSU 上执行,否则在该周期内不采取任何动作。
3)系统效用。累计任务时延、能耗约束、费用开销三者的子效用作为奖励函数评价动作空间与状态空间的映射关系,结合式(21),在时刻t系统立即效用可表示为:
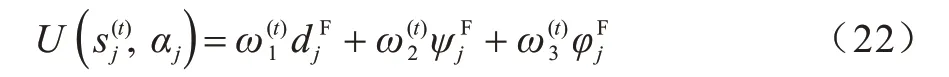
进一步地,由于当前的动作仅受前一时刻状态影响,当前状态通过执行某一动作转换到下一状态,因此可利用马尔科夫决策过程来表述。假设状态空间到动作空间的映射为Φ,即Φ()=aj,则系统状态转移概率可表示为:

状态值函数Vπ(s) 和状态动作函数Qπ(s,α) 可以表示为:

其中,π表示SVU 当前采取的策略,γ表示折扣因子。根据式(25)和贝尔曼公式的定义,进一步可得到式(26):

基于值迭代或策略迭代的传统方法需要智能体获得全局信息,不适用于信息特征变化频繁的车联网场景。由于Q 学习在与环境交互的过程中通过局部信息不断地试错来找到最优行为,因此SVU 可以通过Q 学习最大化长期效用获得最佳的控制决策。但结合式(22)和式(26)可知此方法存在以下两点不足:1)状态空间的大小会随着训练的轮数大幅增加,影响收敛性;2)出现梯度消失或梯度爆炸现象,导致模型退化。本文对此做以下改进:
1)采用经验重放策略。
将智能体在环境探索过程中获得的经验数据存放在经验池中,在后续训练深度神经网络的过程中随机采样更新网络参数。经验池表示为Μ(j)={m(j-M+1),m(j-M),…,m(j)},存放的经验数据元组表示为m(j)=。SVU随机采样⊆M(j)输入神经网络进行训练,而非直接利用连续样本进行训练。更新规则可表示为:

2)采用边云协同思想及线性Q 函数分解理论。
由式(22)可知,系统效用由任务时延、能耗约束和费用开销累加形成,需要训练大量的参数,不可避免地需要更多的计算资源和存储资源,并且会增加训练时间。因此,本文利用边云协同思想,将神经网络的训练过程放置到云端,利用经验回放池的数据进行训练。此外,采用线性Q 函数分解理论对式(22)做进一步改进。设智能体指示符K={1,2,3}分别对应3 个效用分量,式(22)可表示为:

进一步地,式(25)可以表示为:

因此,式(27)所示的更新规则改进为:

5 仿真结果与分析
5.1 仿真设置
利用MATLAB 仿真平台对所提边云协同卸载方案进行仿真评估。仿真遵循Manhattan 模型描述的参数设置并按照MEC 白皮书[6]相关规定构建系统模型,使用SNIA 云服务器记录所有数据集,并提供云端的计算服务支持边缘节点参数更新。具体仿真参数见表1。

表1 仿真参数Table 1 Parameters of simulation
5.2 结果分析
为验证所提方案的收敛性并比较不同学习率对其收敛性的影响,将时延作为参照结果。由图2 可以看出:当学习率为0.01 时,收敛到一个局部最优解时延较大;缩小学习率至0.005 可以得到较大的性能提升,但收敛速度变缓;学习率为0.001 时,在收敛结果上仍有较大提升。考虑到更小的学习率会导致长时间无法收敛,本文采用0.001 的学习率作为后续实验参数。

图2 不同学习率下训练周期与时延的关系Fig.2 The relationship of training period and time delay under different learning rates
不同方案的累计能耗随训练周期的变化趋势如图3 所示,其中累计能耗的大小代表了计算任务迁移量。可以看出:对照组没有利用云端技术,边缘节点累计能耗在短时间内快速上升,随着任务量逐步均衡迁移而达到稳定状态,因为路边单元的计算能力强于车辆节点,所以仅V2I 卸载方案略优于仅V2V 卸载方案;本文方案利用边云协同优势,在训练过程中参数更新及时,局部参数的快速迭代能拟合得到全局最优解,因此在较短的时间内就达到了系统功耗均衡。

图3 不同方案训练周期与能耗的关系Fig.3 The relationship of training period and energy consumption under different schemes
不同方案系统效用随计算任务到达率及频谱分配因子的变化趋势如图4 所示。可以看出:一方面,系统效用随计算任务到达率先增后减,在计算任务到达率为0.6 时达到最佳状态,此时资源队列较优,使得执行子效用对系统效用倾向性较大,通过调整子效用系数来应对不同场景需求,本文对于执行时间有强约束,故将子效用系数设置为ω=[0.6,0.2,0.2];另一方面,计算任务生成率越高也能提升系统效用,任务数据传输不易丢包。相较于仅V2V 卸载和仅V2I 卸载方案,本文方案具有明显优势。在对照组实验中,当计算任务达到率仅为0.5 时资源队列就达到饱和状态,计算任务已处于排队状态。

图4 不同方案计算任务到达率与系统效用的关系Fig.4 The relationship of system utility and computation tasks arrival rate under different schemes
不同频谱分配因子m下系统效用与计算任务到达率的关系如图5 所示。可以看出,尽管本文方案计算任务到达率为0.6 时系统效用已达到最大值,但随着到达率的增加仍保持接近最佳值,体现了本文方案的有效性。

图5 不同频谱分配因子下计算任务到达率与系统效用的关系Fig.5 The relationship of computation tasks arrival rate and system utility under different spectrum allocation factors
不同训练周期和子效用系数设置下时延与能耗的关系如图6 所示。可以看出:一方面,随着训练周期增加,即训练的迭代次数的增加能反馈给智能体更完备的神经网络结构,使得计算任务的卸载能耗有所下降,但值得注意的是,云端训练的开销能否得到有效供给是一个开放性问题,在本文中训练周期为4 000 时达到了收敛状态;另一方面,随着子效用系数ω2的增大,系统的能耗也逐渐增大。费用开销子效用系数ω3对于能耗的影响较大,ω3值增大导致能耗快速增长。

图6 不同训练周期和子效用系数设置下时延与能耗的关系Fig.6 The relationship of delay and energy consumption under different settings of training period and sub-utility coefficient
6 结束语
本文提出一种基于多智能体强化学习的车联网任务卸载方案。采用随机几何理论对资源队列进行控制,从而降低任务排队时延,同时分离云端训练神经网络和节点决策神经网络,使云端能够更精准地提取环境特征,节点端则定时根据云端反馈的优化参数进行在线决策。仿真结果表明,与单一固定边缘的计算策略相比,该方案能够有效减小时延和能耗并且降低计算复杂度。下一步将结合节点缓存技术设计更高效的车联网计算任务卸载方案。

