图神经网络综述
王健宗,孔令炜,黄章成,肖 京
(平安科技(深圳)有限公司联邦学习技术部,广东深圳 518063)
0 概述
近年来,深度学习技术逐渐成为人工智能领域的研究热点和主流发展方向,主要应用于高维特征规则分布的非欧几里德数据处理中,并且在图像处理、语音识别和语义理解[1]等领域取得了显著成果。图的概念起源于18 世纪著名的柯尼斯堡七桥问题,到20 世纪中期拟阵理论、超图理论和极图理论等研究蓬勃发展,使得图论[2]在电子计算诞生前已成为重要的数学研究领域。作为一种关系型数据结构,图在深度学习中的应用在近年来受到越来越多的关注,图的演进历程被分为数学起源、计算应用和神经网络延伸3 个阶段。随着计算机的出现和机器计算时代的到来和发展,图作为一种能够有效且抽象地表达信息和数据中的实体以及实体之间关系的重要数据结构得到了广泛应用,图数据库有效解决了传统的关系型数据结构面对大量复杂数据存在的建模缺陷多、计算速度慢等问题,图数据库也成为热门的研究方向。图结构[3]可以将结构化数据点通过边的形式,依照数据间的关系将不同类型和结构的数据节点相连接,因此被广泛地应用在数据存储、检索以及计算中。基于图结构数据,知识图谱[4-7]可以通过点和边的语义关系精确地描述现实世界中实体之间的关联关系,包括知识抽取、知识推理、知识图谱可视化等研究方向。图计算具有数据规模量大、局部性低、计算性能高等特性,图计算算法[8-9]主要分为路径搜索算法、中心性算法、社群发现算法3 类,其在关系复杂的大规模数据上具有时效性强和准确度高的性能表现,并且在社交网络、团体反欺诈和用户推荐等领域具有重要的应用。
图神经网络的研究主要集中于相邻节点信息的传播与聚合。2013 年,BRUNA 等人提出的基于图论的图神经网络[10]和DEFFERRARD 等人提出的频域图卷积神经网络[11]受到了业界的广泛关注。2018年,BATTAGLIA 等人[12]在关系归纳偏置和深度学习技术的基础上,提出面向关系推理的图网络概念,以期将深度学习的端到端学习方式与图结构的关系归纳推理理论相结合,解决深度学习无法处理的关系推理问题。2019 年,ZHANG 等人[13]从半监督和无监督角度对基于图结构的深度学习技术进行综述,ZHOU 等人[14]从传播规则和网络结构等角度分析图神经网络模型及其应用,WU 等人[15]对比了时域和空间域的图卷神经网络结构。针对图神经网络存在的其他问题,研究人员给出了很多解决方案,随着对图神经网络领域更加深入的研究与探索,人工智能领域的版图将得到更大扩展。本文分析并比较6 种图神经网络结构的优劣,重点讨论基于不同信息聚合方式的图神经网络结构及5 种图神经网络的研究领域,并对未来的发展方向进行展望。
1 图结构
1.1 图结构定义
图神经网络处理的数据是在欧氏空间内特征表示为不规则网络的图结构数据,基本的图结构定义为:

其中,图G由数据节点集合vi∈V、连接节点集合eij=(vi,vj)∈E组成,其映射到高维特征空间fG→f*所得到的邻接矩阵表示为AN×N。
1.2 图结构分类
对于图的构成而言,可以从空间和时间两个角度出发进行分析。从空间角度,图结构的变化可以通过节点和边进行区分,如边异构的有向图、权重图、边信息图及节点异构图。从时间角度,引入节点在时序变化中的差异形成时空图结构。5 种典型的图结构示例如图1 所示,不同图结构的结构特征、图模型和应用场景如表1 所示,具体描述如下:
1)有向图是指在图结构中连接节点之间的边包含指向性关系,即节点之间的关联就包含了方向的传递性关系,对于图神经网络而言,这种传递关系和基于深度学习的神经网络神经元中信号传递的结构近似,有向图的输入是各个节点所对应的参数。针对单向图的处理方式,MATHIAS 等人[16]提出适用于单向图的无监督节点标签判断方式。对于有向图中可能存在的双向关系,KAMPFFMEYER 等人[17]提出通过双向权重对应的双向邻接矩阵表示双向关系的模型ADGPM,利用知识图谱解决零样本学习问题,实现对神经网络传递更多的信息。
2)权重图是指图结构中的边包含权重信息,可以有效地描述节点之间相互作用的可靠程度,定量表示关系的连接程度。对于权重图的处理,DUAN 等人[18]通过对动态权重有向图进行归一化处理,利用节点之间的关联关系权重动态实现信息挖掘。
3)边信息图是指对于存在不同结构边的图结构,节点之间的关联关系可以包含权重、方向以及异构的关系,如在一个复杂的社交网络图中,节点之间的关联关系既可以是单向的关注关系,也可以是双向的朋友关系。对于包含复杂边信息的图结构而言,复杂的关联关系不能直接通过简单的权重约束来表示,BECK 等人[19]提出一种将原始图转换成二分图的模型G2S,在处理自然语言处理任务时,将每一个词节点之间的关联关系采用独立编码方式,大幅提升了语义理解效率。
4)节点异构图是指在图G中的节点属于多个不同类型的图结构,这种图结构通常根据异构节点类型对节点进行向量表示,也可以通过独热编码等编码方式实现节点的向量表示。ZHANG 等人[20]提出一种通过元路径对异构图结构的文本进行编码的方法,该方法根据异构节点类型对邻居节点进行分组,适用于节点分类[21]、文本向量化表示以及相似度搜索等任务。
5)时空图是一种属性图结构,其特点是高维特征空间f*中的特征矩阵X会随时间变化,本文将其定义为G*=(V,E,A,X)。图结构随着时间序列的引入,可以有效处理包含动态和时序关系类型的任务,YAN 等人[22]提出一种基于时空图卷积神经网络的骨架运动检测方法,YOU 等人[23]基于视频标签节点之间邻接关系的相似度,提出一种利用多标签视频分类的图神经网络方法。

图1 5 种典型的图结构示例图Fig.1 Example graphs of five typical graph structures

表1 5 种典型的图结构对比Table 1 Comparison of five typical graph structures
2 图神经网络
图神经网络对于非欧几里德数据在深度学习中的应用具有重要作用,尤其是利用图结构在传统贝叶斯因果网络上可解释的特点,对于定义深度神经网络关系可推理、因果可解释的问题有较大的研究意义,因此如何利用深度学习技术对图结构的数据进行分析和推理引起了学者们的广泛关注。本文对现有的图神经网络结构进行总结与归纳,给出一个通用的图神经网络结构,如图2 所示,将图神经网络推理过程通过图节点预表示、图节点采样、子图提取、子图特征融合、图神经网络的生成和训练子过程进行表示,具体步骤如下:
1)图节点预表示:通过图嵌入方式对图中每一个节点进行嵌入表示。
2)图节点采样:对图中每个节点或存在的节点对的正负样本进行采样。
3)子图提取:提取图中每一个节点的邻节点构建n阶子图,其中n表示第n层的邻节点,从而形成通用的子图结构。
4)子图特征融合:对每一个输入神经网络的子图进行局部或全局的特征提取。
5)图神经网络生成和训练:定义网络层数和输入输出参数,并对图数据进行网络训练。

图2 图神经网络通用结构Fig.2 General structure of graph neural networks
本文将从频域和空间域角度研究图卷积网络(Graph Convolutional Network,GCN),对比多种图卷积神经网络[21]的发展历程,介绍门控图神经网络[24]、图注意力网络[25]、图自动编码器网络[26]、空图神经网络[27]和图嵌入网络[28]的模型结构和实现方式,并从聚合方式、网络结构和应用优势的角度对比分析上述图神经网络模型的差异。
2.1 图卷积神经网络
深度学习技术的流行与卷积神经网络的广泛应用密不可分,图卷积神经网络从特征空间来看可以分为频域和空间域两类。图卷积神经网络将原始图结构的数据G=(V,E)映射到一个新的特征空间fG→f*。以单层前向传播图卷积神经网络为例,第i层神经网络的特征用ωi表示,在计算图结构中的每一个节点vi时,每一层神经网络的输出Hl+1都可以通过非线性函数f(⋅, ⋅)表示为Hl+1=f(Hl,A),其中A为特征邻接矩阵。通过非线性激活函数ReLU=σ(⋅)实现图卷积神经网络结构,其分层传播规则如下:
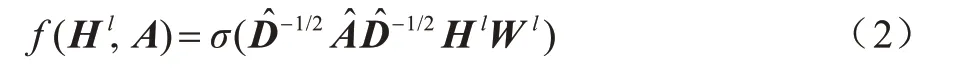
2.1.1 基于频域的图卷积神经网络
频域的图卷积神经网络基于图信号处理[29],将图神经网络的卷积层定义为一个滤波器,即通过滤波器去除噪声信号从而得到输入信号的分类结果。在实际应用中只能用于处理无向且边上无信息的图结构。将输入信号的图定义为可特征分解的拉普拉斯矩阵,进行归一化和特征分解后可以表示为通用结构UAUT,对角矩阵A由特征值λi按序排列组成。BRUNA 等人[10]提出频域图卷积神经网络,并定义卷积层函数。假设频域图卷积神经网络为图信号处理中的滤波器,特征分解需要至少O(n3)的计算复杂度和O(n2)的存储空间,当输入图数据为稀疏矩阵时,可以通过随机特征分解等方法在保证精度的情况下将时间复杂度降至O(n2r+r3),其中r为近似矩阵的秩,远小于n。
HENAFF 等人[30]提出基于插值内核的图卷积神经网络。在频域卷积神经网络的基础上构建无监督和有监督推理预测方案,从图神经网络通用结构中可以看出,图节点预表示可以根据数据预测相似性矩阵,该方法也适用于大规模图像和文本分类等问题中。
DEFFERRARD 等人[11]提出基于切比雪夫多项式的频域卷积滤波器ChebNet,其中切比雪夫多项式是由特征值对角矩阵的项所组成,通过将切比雪夫展开式Ti(x)替换原始GCN 中通用频域卷积滤波器gθ的特征分解部分,从而有效避免特征分解的计算部分,将计算复杂度从O(n3)降低至O(LE),其中,E为输入图G中边的数量,L为多项式阶数且与图的大小成正比。一阶切比雪夫图卷积神经网络[27]则是利用一阶切比雪夫展开更好地提升了网络的计算效率。针对包含复杂属性的节点异构图,可以通过图卷积神经网络来实现节点的聚类。为提升属性图的信息提取性能和模型效果,ZHANG 等人[31]提出AGC 自适应图卷积方法,利用高阶图卷积获取全局聚类结构来定义k阶图卷积,从而实现对于复杂异质图的处理。
2.1.2 基于空间域的图卷积神经网络
与深度学习中卷积神经网络对图像的像素点进行卷积运算类似,基于空间的图卷积神经网络通过计算中心单一节点与邻节点之间的卷积来表示邻节点间信息的传递和聚合,从而生成新的特征域节点表示。SCARSELLI 等人[32]提出一种利用基于相同图卷积结构的循环函数,递归地实现空间图卷积神经网络的收敛方法,该方法可以支持节点和边上分别包含特定属性的异构图,是契合传统卷积神经网络基本思想的方法。DAI 等人[33]提出随机稳态图神经网络迭代算法SSE,对于每个拥有不同数量邻节点的节点,在每次卷积迭代过程中利用双向权重矩阵W1、W2更新节点的特征表示。
随机稳态图神经网络不支持边上包含的信息,通过两个权重函数分别对全部的节点集合v∈VN和包含信息的节点集合v∈VM进行卷积处理,从而使得图卷积神经网络的迭代效率得到提升。图结构数据中的节点存在极多的关系导致参数数量过多,在此情况下,引入基础分解和块对角分解两种方式可以有效解决过拟合问题。关系图卷积神经网络可以应用于以节点为中心的实体分类问题和以边为中心的链接预测问题中。
ATWOOD 等人[34]提出基于图结构的深度卷积神经网络(Deep Convolutional Neural Network,DCNN),通过卷积传播方式扩散性地扫描图结构中的每一个顶点,替代了一般图卷积神经网络基于矩阵特征的卷积形式,DCNN 的参数是由搜索深度而不是节点在图结构中的位置决定,可以用于节点、边以及图结构等多种分类任务,但由于计算转移概率的时间复杂度较高,并且不适用于大规模的图结构数据,因此ZHUANG 等人[35]在传播和邻接矩阵两种卷积结构的基础上提出一种双路图卷积神经网络,将半监督图卷积[29]和转移概率的正逐点互信息(Positive Pointwise Mutual Information,PPMI)矩阵作为卷积运算邻接矩阵来更好地提升模型的信息抽取效果[36-37]。
表2 从频域和空间域角度对图卷积神经网络进行分析对比,其中,√表示具备可扩展性,×表示不具备可扩展性。频域图卷积神经网络主要依赖频域矩阵的特征分解,对比网络包括Spectral Network[26]、ChebNet[29]、1stChebNet[20]、AGCN[38]和AGC[31],而空间域图卷积神经网络主要借助邻节点特征信息的聚合来定义图数据上的卷积运算,对比网络包括GNN[32]、DCNN[34]、MGCN[39]、SSE[33]、DGCN[35]、PinSage[40]、MPNN[37]、GraphSage[36]和Fast-GCN[41]。同时,关于图卷积神经网络优化方式的研究也有很多,针对高阶图卷积在空间域图卷积中性能较差的问题,引入稀疏邻域来替代频域图卷积的MixHop[42]。

表2 图卷积神经网络对比Table 2 Comparison of graph convolutional neural networks
2.2 门控图神经网络
目前,基于门控机制的递归神经网络的研究也得到学者们的广泛关注,例如基于门控循环单元(Gated Recurrent Unit,GRU)的门控图神经网络(Gated Graph Neural Network,GGNN)[43]通过GRU 控制网络传播过程中固定步数的迭代循环来实现GGNN 结构,利用节点来建立邻节点之间的聚合信息,然后基于循环门控单元实现递归过程中每个节点隐藏状态的更新。
TAI 等人[44]提出基于子节点的树状长短时记忆网络(Tree-LSTM)用于处理图神经网络中的语义表示问题。门控图神经网络除了基于门控循环单元和LSTM 的基础模型外还有很多变种,例如:YOU 等人[45]利用分层循环递归网络分别生成新的节点和节点对应的边,从而将图递归神经网络应用于图生成问题;PENG 等人[46]提出利用不同的权重矩阵来表示不同标签的图长短时神经网络结构;MA 等人[47]将时间感知LSTM 与图神经网络相结合,利用LSTM来更新两个关联节点和对应的邻居节点的表示,提出动态图神经网络,更好地解决传播效应问题。
2.3 图注意力网络
对于图神经网络中的注意力机制,借助于注意力模块取代一般图卷积神经网络中的卷积激活器,在不同方法中结合门控信息来提升注意力机制感受域的权重参数,达到更好的推理和应用性能。
图卷积神经网络实现了对图结构数据的节点分类,而注意力机制目前在自然语言处理领域有着非常好的效果和表现。对于图注意力机制[25,48]而言,邻居节点的特征累加求和过程与图卷积神经网络完全不同,通过全局注意力机制替代卷积分层传递的固化操作,可以有效选择在图结构中更为重要的节点、子图、模型、路径分配更大的注意力权重[48]。
图注意力网络中的注意力权重被表示为,对于第l层网络而言,定义节点为=Wlhi,其中,hi是注意力模型中的节点向量,Wl表示为一个可变化的线性变换参数,那么节点间的注意力分数就会根据注意力权重的不同进行迭代。与图卷积神经网络的分层传播规则不同,图注意力网络将原有的常数参数替换为表示邻节点权重的注意力参数。
ZHANG等人[49]提出一种通过卷积子网络来控制分配权重的自我注意力机制,利用循环门控单元解决流量速度预测问题。LEE等人[50]提出结合LSTM与注意力机制的图节点分类方法。ABU-EL-HAIJA等人[42]提出一种注意力游走方法,将图注意力机制应用于节点嵌入中。
在现实世界中信息在被表示成节点和边构成的拓扑结构时通常是异构的,广义上被定义为异构信息网络(Heterogeneous Information Network,HIN)[51],而现阶段的图神经网络多数聚焦于同构图的处理分析,对于节点异构和边异构的图结构而言,巨大的信息量和复杂的网络结构带来了更大的挑战和研究价值。WANG 等人[52]提出一种基于注意力机制的异构图注意力网络,将节点和边的异构性表达为不同类型的语义信息,通过节点层的注意力来判断相同属性邻节点的重要性,同时利用语义层的注意力选择有意义的元路径,节点层利用注意力来表示不同节点的重要性。图注意力网络的研究还集中于图像语义推理、上下文推理等方面。具体地,YANG 等人[53]在处理利用自然语言来表示图像中的描述对象问题时,通过抽取图像中对象之间的语义关系建立关联图结构,借助动态图注意力网络(DGA)来实现更好的语义推理能力。
2.4 图自动编码器网络
自动编码器是深度神经网络中常用的一种无监督学习方式,对于图结构数据而言,自动编码器可以有效处理节点表示问题。最早的图自动编码器是由TIAN 等人[26]于2014 年提出的稀疏自动编码器(SAE),通过将图结构的邻接矩阵表示为原始节点特征,利用自动编码器将其转化为低维的节点表示。稀疏自动编码问题被转化为反向传播的最优解问题,即最小化原始传输矩阵和重建矩阵之间的最优解问题。在结构深度网络嵌入方法[54-55]中,将损失函数表达为邻接矩阵的形式,证明了两个具有相似邻节点的节点有相似的潜在特征表示,并且结构深度网络嵌入方法引入类似拉普拉斯特征映射来替代目标函数。变分图自动编码器(VGAE)[56]将卷积神经网络应用于图自动编码器结构,对于非概率变体的图自动编码器,定义由随机隐藏变量zi组成的矩阵Z,那么编码器可以表示为Z=GCN(X,A)。结合结构深度网络嵌入的方法,ZHU 等人[57]提出利用高斯分布进行节点表示的方法,并选择EM 距离作为目标损失函数,能够有效地反映距离信息特征。
2.5 时空图神经网络
时空图神经网络作为一种引入了时间序列特征的属性图网络,可以同时获取图结构中时间和空间域的特征信息,每一个节点的特征都会随着时间的变化而变化。本文主要讨论在空间域采用图卷积来提取空间特征依赖的时空图神经网络结构,主要分为传统卷积网络、门控循环网络和图卷积网络3 种时域特征获取方法。图3 给出了图卷积神经网络、图自动编码器网络(以变分图卷积自动编码器为例)和时空图神经网络(以1D-CNN+GCN 结构为例)的网络结构对比,3 种网络结构的构建基础均为图卷积计算单元,其中,φ为矩阵Z和ZT之间的元素距离,MLP 全连接表示多层感知机全连接神经网络。

图3 图卷积神经网络、图自动编码器网络和时空图神经网络结构对比Fig.3 Structure comparison of graph convolutional neural network,graph autoencoder network and spatiotemporal graph neural network
YU 等人[58]在实时交通预测问题中,利用时空图的特性解决交通流的高度非线性和复杂性问题,提出一种时空图神经网络,采用一维卷积神经网络(1D-CNN)沿时间序列X[i,:,:]∈ℝT×N×D传播聚合时域特征,其中,T为时间步长,N为节点数量,D为节点向量维度。同时图卷积神经网络作为每个时间点上的空间信息聚合器,构成如图3(c)所示的时空图神经网络结构。HUANG 等人[27]提出扩散递归卷积神经网络,采用门控图神经网络中的门控递归单元获取时域依赖性。为结合循环单元GRU 获取的时间序列异步信息及图卷积神经网络捕获的空间邻节点信息,SIMONYAN 等人[59]设计一种改进的扩散卷积门控递归单元(DCGRU)结构来更好地提升时空特征的依赖性。
YAN 等人[60]将事件流扩展为图结构中的边信息,通过图卷积神经网络模型同时提取时域和空间域中的信息特征,将运动过程中人体抽象的骨节作为节点进行检测,并且其延续了文献[29]的定义,将分层传播规则延伸为时空图神经网络的输入和输出,从而基于边信息的提取实现时域和空间域信息的提取和学习。
2.6 图嵌入网络
图结构中的每一个节点和边对于深度神经网络而言都是不规则的抽象数据,而通过图嵌入方法对节点和边赋予数值张量,能将图结构类比于深度神经网络所处理的图像数据,赋予的数值就如同图像中像素数量和像素对应的值。在实现图嵌入网络的算法中,最基础的算法就是深度随机游走算法[61],其将语言模型的语义理解任务经过文本分词后得到的词视为图结构中的节点,而连接节点的边则通过随机游走实现。每一次随机游走所连接的节点形成的路径就是由单词所构成的随机句子,这样的随机图结构网络可以通过N维矩阵的形式进行表示。在深度随机游走网络中,随机游走长度通常是需要人为确定的超参数,为解决这一问题,ABU-EL-HAIJA 等人[62]基于深度学习理念,提出基于反向传播的可学习超参数,并引入基于转移矩阵幂级数的图注意力网络结构,通过对上层目标函数的分析来优化超参数的选择,从而实现超参数的可学习性。
现阶段的空间图卷积神经网络受限于网络复杂度和节点表示效果,一般只能用于处理同构图[15],而直接将异构关系抽象为同构图后会损失较多的特征信息。对于属性多元异构网络嵌入,CHEN 等人[63]提出的HGR 模型有效提取了视频文本匹配任务中图数据的全局和局部特征,并且适用于抽象场景图。
表3 从图结构和性能优劣势角度,对7 种图神经网络进行了分析和对比。

表3 图神经网络结构对比Table 3 Structure comparison of graph neural networks
3 图神经网络研究领域
3.1 图生成和图对抗
图生成的目标是基于一组可观察图来生成图,其中的很多网络均为领域特定,例如:在分子图生成方面,一些研究将分子图的表征建模为字符串[64-65];在自然语言处理方面,生成语义图或知识图通常需要一个给定的句子[66-67]。最近,研究人员提出了一些通用方法,例如将图生成过程看成节点或边的形成[68],使用生成对抗网络实现生物分子图的训练[69]和基于随机游走的图生成网络[70]。
图对抗网络的研究主要集中于图网络的可靠性和安全性方面,尽管图神经网络模型取得了一定的研究进展,但通常缺乏可解释性和稳健性,尤其是通过领域特征的聚合方式进行网络构建时需要利用节点敏感信息,因此存在被攻击的风险[71-72]。
3.2 图强化学习
在图强化学习中,学习控制问题通常采用马尔科夫决策过程(Markov Decision Process,MDP)[73]估计长期回报问题。根据图中节点所表述的决策状态,利用转移概率矩阵表示相似性矩阵。通过使用可学习的表示来实现线性逼近值函数,其近似值函数为状态图上第一个拉普拉斯特征映射的线性组合。
DONNAT等人[74]提出的方法基于以节点为中心的谱图小波的扩散来学习节点表示。MADJIHEUREM等人[75]在表示策略迭代(Representation Policy Iteration,RPI)[76]阶段使用原始数据集构建无向加权图。利用有限数量的样本构造图结构,其派生的原始值函数不一定能够反映基础状态空间,但可以通过函数来测量图函数的全局平滑度。当来自平滑函数的值vi、vj驻留在两个连接良好的节点上时,则预期它们之间的距离较小,即图函数具有较高的平滑度。
3.3 图迁移学习
迁移学习是运用已有知识对相关领域问题进行求解的一种机器学习方法。BOSCAINI 等人[77]提出的局部SCNN 模型方法可以提取可变形状的属性。BRUNA 等人[10]提出的图卷积结构是广义SCNN 模型图迁移学习框架的关键组成部分,其借鉴傅里叶变换思想将网格域中的CNN 应用于图结构域。
LEE 等人[78]提出的图迁移学习方法由5 个步骤组成,前3 个步骤根据输入生成图,并从图结构中识别结构特征,后2 个步骤是基于特征学习和图相似性应用迁移学习进行分类和推荐等任务的推理。PAN 等人[79]指出在迁移学习环境中的域由特征空间和概率分布组成,对于给定域可以通过任务来表示具有标签的空间和训练数据预测函数。在两个图域相似的情况下,在迁移图中学习到的内在几何信息可以通过快速建立迁移学习模型,并利用来自异构数据集的图谱特征,大幅提升学习效率。
3.4 神经任务图
任务图[80]通过表示任务的组成与时序来有效执行任务。神经任务图网络[81]将任务图与神经网络相结合,能够更加高效地调度与学习任务。通过视觉模拟学习方法,神经任务图网络将组合任务引入中间任务的表示和策略中,在照片渲染的模拟环境和现实世界的视频数据集中,神经任务图的表现比非结构化表示方法以及人工设计的分层结构化表示方法效果更好。神经任务图显著提高了复杂任务的运行效率,通过神经任务图的组合实现从原始视频数据到复杂任务的仿真,并在神经任务图训练过程中利用节点的嵌入表示解决动作模拟任务中缺少训练数据的问题。
3.5 图零样本学习
图神经网络在零样本学习的图像和视频分类任务中具有广泛应用,通过借助图结构中节点之间的强关联性,可以有效泛化样本缺乏情况下需要生成预测新类别的问题。基于知识图的零样本学习是利用现有知识库或者知识图谱中结构化的关系信息,在未知任何样本数据的情况下进行推理学习解决样本分类的问题。
WANG 等人[82]提出基于图卷积神经网络的零样本图像分类方法,通过图卷积处理未知权重信息的知识图。对于图神经网络而言,在解决零样本学习问题的过程中,当知识传播层数较高时会降低处理效率。LEE 等人[83]提出同时预测多个未知标签的零样本学习方法,有效地解决了多样本分类问题。
表4 对图神经网络的研究领域进行简要的概述和总结。

表4 图神经网络的研究领域总结Table 4 Summary of research fields of graph neural networks
4 图神经网络应用方向
图神经网络在不同任务和所处的时间、空间或频域中均具有广泛应用,主要分为文本处理、图像处理、图系统、动作检测4 个应用方向。
4.1 图神经网络在文本处理中的应用
对于文本向量化表示而言,图神经网络可以对句子和词级别的文本进行处理,文献[25]通过密集图传播模块来实现距离较远的文本节点的关联关系表示。文献[61-62]则通过图嵌入的方式来实现节点的向量化表示,用于文本词向量和句向量的推理。
在文本分类领域,文献[84]利用基于双向图长短时记忆网络,实现了每个文本词向量的双向状态表示,从而达到了更好的文本分类效果。文献[85]通过递归正则化的方式,更有效地获取非连续语义和长距离语义。
图神经网络也可以应用于文本的序列标注。对于文本图结构的词节点而言,每个节点的序列生成可以通过图生成网络的方式来实现,文献[83]通过节点对象强化的图生成网络OR-GAN 进行序列生成。文献[86]利用图长短时记忆网络对句法信息中文本节点间的关联关系进行建模,得到每个词节点的潜在特征用于序列标注。
关系推理[87]是指从复杂的语义信息中推理出文字节点之间的关联关系。文献[19]通过关系图卷积R-GCN 来完成文本实体间关系的抽取和属性分类。文献[46]利用图长短时记忆网络构建文本序列中跨多个句子时的N元关系,通过上下文中文本实体之间的关系进行任务推理。
4.2 图神经网络在图像处理中的应用
在图像分类的任务中,零样本和少样本学习的任务通常需要借助知识图谱的先验知识来提升识别效果。图神经网络有效提升了知识图谱的推理效率。文献[17]通过深度图传播方法将异构图结构用于知识推理,利用中间节点的特征信息来优化知识的稀疏度。文献[85]借助图神经网络将少样本学习的任务转化为可以端到端训练的监督学习任务。
4.3 图神经网络在图系统中的应用
对于推荐系统而言,用户与项目的关系可以构成二部图,用户与用户之间可以构成社交网络,项目与项目则可以构建知识图谱和异构图,通过图神经网络可以为用户进行商品推荐。文献[78]利用基于上下文的图自注意力网络实现了高效的会话推荐。
如何构建和提升知识图谱的应用效果一直是图领域备受关注的研究方向。文献[21]利用知识图谱实现了基于知识迁移的图小样本学习方法。文献[82-83]均通过知识图谱的推理来实现和完成图零样本学习任务。文献[88]介绍了如何挖掘知识图谱以实现大规模企业级应用。
作为生物学的研究领域,分子的构成是天然的图结构。文献[20]利用端到端的图卷积网络实现了圆形指纹的分子特征提取方法。文献[39]进一步将图卷积方法应用于生物分子图领域。文献[69]提出基于图生成网络的分子图生成方法,可以有效模拟化学分子的合成。
4.4 图神经网络在动作检测中的应用
通过视频序列来实现任务预测是时序图领域的重要应用方向之一。文献[77]提出基于共轭任务图结构的策略生成方法,实现了基于给定的演示视频推理完成未知的任务。文献[89]提出视觉空间注意力机制的图卷积方法来完成视觉理解任务中人与对象交互定位HOI 的任务。文献[22]通过时空图神经网络实现了基于骨节运动的动作检测。
表5 对图神经网络的应用方向进行简要的概述和总结。
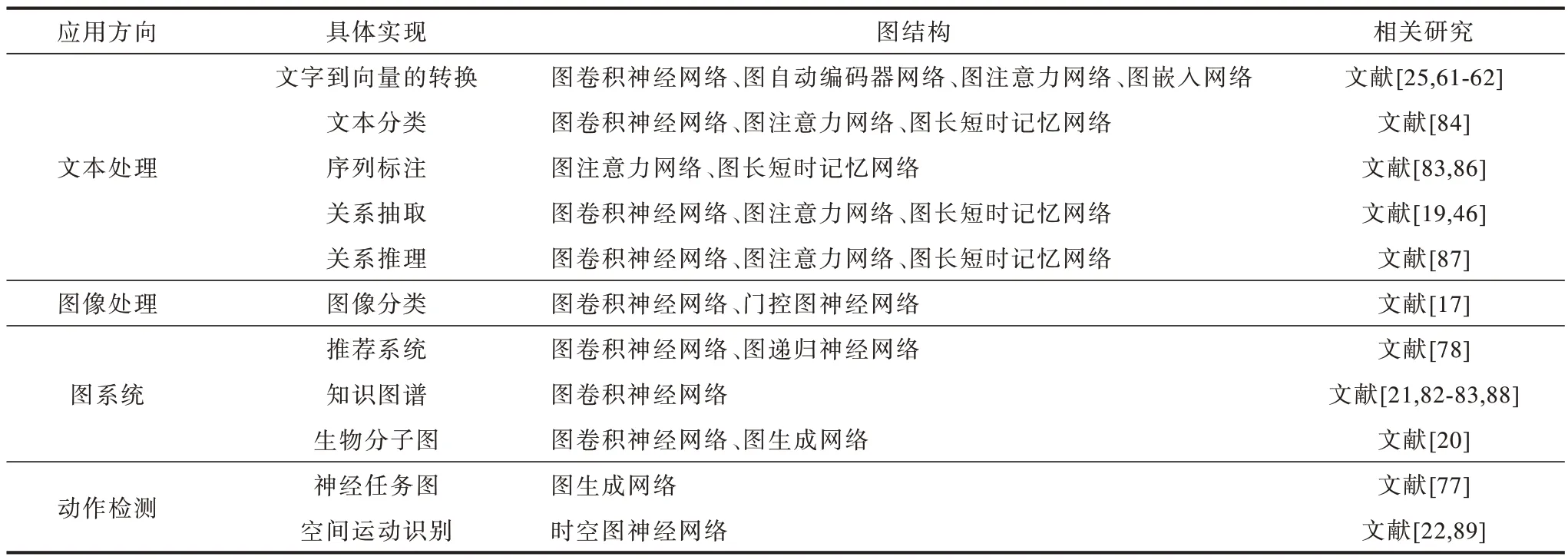
表5 图神经网络的应用方向总结Table 5 Summary of application directions of graph neural networks
5 未来发展与展望
随着图神经网络研究和应用的不断深入,其发展方向主要包括网络结构优化、理论可解释性强化及数据结构丰富化,具体内容为:
1)与传统深度学习相比,图神经网络的研究和应用方向有较大的拓展空间,由于其对于知识图谱、推荐系统等大规模系统性应用具备迁移性、可强化性等特点,并且对于动态任务具有泛化能力,因此能够将图神经网络与深度学习实现有效关联,更高效地利用图结构数据。
2)深度神经网络结构的本质是对数据不断提取高维的抽象特征,将图神经网络结构的关联性特征与传统贝叶斯因果关系网络相结合,以期实现对深度学习神经网络结构的可解释性证明。
3)现阶段有关图神经网络结构的研究多数受限于关系型结构在高维空间中的特征可解释性,而对于提升图神经网络深度的研究较少,深度学习的巨大成功得益于其深层的网络结构能提取更高维度的特征信息。图神经网络在结构上对特征信息进行抽象概括的同时,需要探索加深网络结构的方式,以增强其对于高维特征信息的提取能力,进一步提高网络性能。
4)扩大图神经网络的感受野能有效提升图神经网络的推理性能。神经元感受野可使网络输出的特征值更好地归纳局部和全局特征,从而实现更快的学习收敛速度和更好的网络预测效果。
5)在网络节点中引入更多的数据类型,突破通过节点先验信息决定图神经网络的最终学习效果。将定性、离散或概率型数据以图的形式引入到图神经网络中,增强图网络模型对真实数据分布的刻画能力。
6)提升图神经网络的动态性和异质性,对于具有复杂图结构的异质图和结合时序性的动态图具有更丰富的应用场景。
6 结束语
本文回顾图神经网络的发展历程,分析并比较基于不同信息聚合方式的图神经网络结构,讨论图神经网络与深度学习技术相结合的研究领域,并对图神经网络的应用方向进行阐述。后续将从图神经网络结构的深度和复杂度、异质图的高效分析与处理以及利用节点和边信息的传递实现图神经网络的可解释性等方面做进一步探索,以期优化图神经网络的数据结构、提升算法性能及增强理论可解释性。

