多量级应急数据无监督离散化方法研究

高天宇，王庆荣，杨 妍，马辰坤

（兰州交通大学电子与信息工程学院，兰州 730070）

0 概述

应急信息化响应是国家应急管理体制的发展趋势，数据处理与分析方法作为应急信息化响应的基础，被应用于应急工作的各个阶段。分析应急数据的特点是应急数据处理与分析的合理性保障，连续数据的离散化是数据分析与挖掘的关键预处理方法，其决定最终数据处理与挖掘结果的质量。

连续数据的离散化方法包括有监督离散化方法和无监督离散化方法。常用的有监督离散化方法包括信息熵［1］、粗糙集［2］以及类-属性关联性［3-5］等离散化方法。信息熵离散化方法是一种基于数据混乱程度的不确定性计算方法；粗糙集离散化方法能较好地处理数据边界的不确定性；类-属性关联离散化方法可应用于数据的自动离散和混合过程［6-7］。无监督离散化方法主要包括等宽离散化、等频离散化、近似等频离散化［8-10］以及聚类离散化［11］等方法。等宽离散化方法能在不同区间保持原数据分布进行离散，操作灵活简单；等频离散化方法是基于数据频率分布进行离散；聚类离散化方法是根据数据分布采用层次聚类方式进行离散。

目前关于有监督离散化方法的研究重点针对离散化方法特点进行［12］，对无监督离散化方法的研究主要围绕数据特点展开［13］。然而现有无监督离散化方法对应急数据特点考虑不足，其采用的时间序列离散化［14］方式不适用于多量级应急数据离散。此外，在无监督离散化方法中，当应急数据量小且数据间差异较大时，如果仅以离散系数为指标进行离散，则会出现大量的离散类数据，导致离散结果失去指导意义。当集中分布的数据存在多个量级差异时，现有无监督离散化方法难以找到全部有效的量级变化点。

针对应急数据多量级差异的特点，本文提出一种无监督的多量级应急数据离散化方法。在难以获得应急数据的关联数据时，不考虑应急数据的复杂性与数据之间的关联性，采用拟合函数结合二阶导数计算得到数据截断点，移出较大数据更新待离散数据集，并重复此操作直到完成全部数据的离散。

1 多量级应急数据离散化

应急数据处理较困难的主要原因在于未针对数据特点分别对其进行处理，缺少对隐藏数据特点的深度剖析。将连续数据转换为非连续数据是一种从数据中获取信息的方法，称为数据离散化。连续数据可通过离散化被处理为多个离散类数据，离散后集中数据类型的个数即为数据离散类个数。离散化作为一种有效的数据预处理方法，其结果对数据分析结果有本质影响［15］，在数据处理中需根据数据特征进行离散化［16］。在离散化时可采用静态、分类或者动态组合等不同策略，合理的策略有助于有效挖掘数据特点［17］。

1.1 多量级应急数据

应急数据是一种特点明显的数据，其噪声多且在相同数据集内数据之间差异大，对聚类边界与离散点的分析较困难［18-19］。

在应急数据离散化过程中，具有多量级差异的数据最难离散。将数据由大到小排序后，可看到数据之间差异变化存在多个数据量级跳跃，多量级数据离散化即找到这些量级跳跃的点。数据集中数据之间存在多个量级，其中较小数据的量级差异被隐藏，如图1 所示（虚线框为待离散的应急数据集）。当数据1 存在时，数据2 易被归为其他离散类，若去掉数据1 后再离散，则会发现数据2 与其他数据并非同一个离散类。

图1 较小隐藏数据的量级差异显现过程Fig.1 Process of showing the magnitude difference of hidden smaller data

量级差异在传统数学中主要指以“10”为幂的数据之间的差异，然而在实际研究中量级差异并不局限于此，为更好地还原事件特征，需根据实际情况重新定义量级来保留更多数据特性［20］。应急事件中各因素的细微变化均会造成应急数据之间的巨大差异，其中存在多个量级变化点，利用传统方法难以找出这些变化点。为此，本文提出一种找出隐藏变化点的数据离散化方法，下文先对离散化数据截断点的确定进行介绍。

1.2 多量级离散化方法

为找出数据集中各个量级的变化点，先对数据按照大小进行排序，再判断数据开始突增的位置，并将该位置作为截断点的截断数据集，使截断数据归为一个离散类，并将剩余数据作为新数据集，然后重复上述操作直到达到所需离散量或者数据每个离散类的离散系数符合要求为止，如图2 所示。

图2 多量级数据的离散化过程Fig.2 Discretization process of multi-magnitudes data

在多量级数据离散化过程中，每找出一个截断点就确定并去除一个离散类，然后在剩余数据中继续寻找截断点，如此反复最终完成动态的离散，同时根据需要对离散系数大于阈值要求的离散类数据重新计算截断点并再次进行截断。

1）确定拟合函数的多项式

使用多项式对数据进行拟合，计算公式如下：

其中，x、y分别为被拟合函数的自变量和因变量，α、β、γ、η、σ为待定系数。

2）确定数据截断点

若将数据中突增的数据截断并找到一个截断点，则可显示出当前较小数据之间的量级差异。该截断点为数据突增的起始点，截断点的斜率等于拟合函数最大值与最小值连接线所在直线的斜率，对多项式y求导如下：

截断点的判定式如下：

其中，k为截断点的导数。

对多项式导数进行回归计算得到截断点的位置，计算公式如下：

其中，突增点x_j是数据离散化所需的一个截断点。

3）根据步骤1 和步骤2 得到截断点后，从截断点进行数据截断，并将较大的数据归为一个离散类，其他数据重新执行步骤1 和步骤2 计算下一个截断点，在数据呈现均匀分布后，统计所有离散类作为最终离散化结果。

2 实验与结果分析

本文进行多量级应急数据离散实验，数据源自国家地震科学数据共享中心、国家数据网、中国地震台网、中国应急信息网以及大量的相关新闻报道和论文数据，通过筛查得到99 个应急数据用于本文研究。表1 为我国不同地区地震伤亡人数相关影响因素统计情况。

表1 伤亡人数相关影响因素统计情况Table 1 Statistical situation of influencing factors related to number of casualties

2.1 结果分析

2.1.1 多量级数据离散化

本文对地震案例中伤亡人数与灾区乡镇数进行离散化，所有案例的伤亡人数统计结果如图3 所示。其中，横坐标为地震案例序号（以震发地省会名称拼音排序，所有案例均从第0 个开始计数）。可以看出，序号为6 的案例伤亡人数最多，其他大部分案例伤亡人数较少。在数据处理过程中，因为存在较大数据，所以较小数据之间的差异被隐藏。

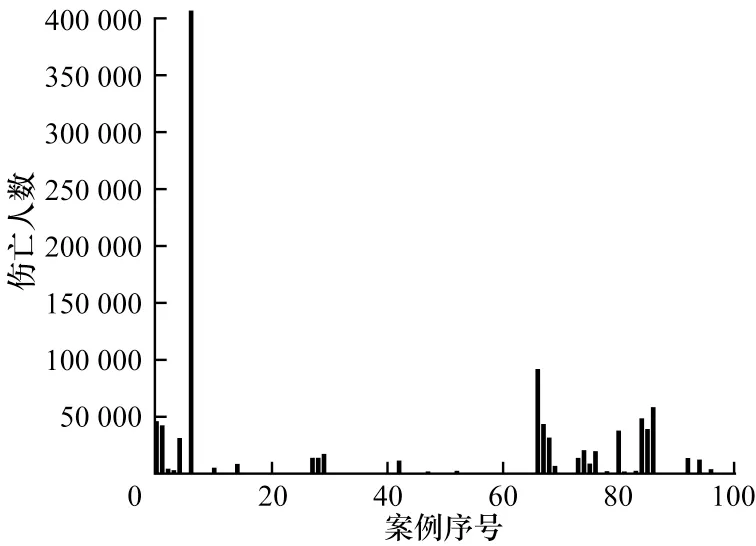
图3 伤亡人数Fig.3 Number of casualties

图4 为将地震案例中伤亡人数由小到大排序的结果。为体现图1 中的数据量级差异，从图4 中随机找一个截断点68 对较大数据进行截断，剩余数据的分布如图5 所示。由图5 可以看出，去掉部分较大数据后，剩余数据仍呈现指数函数的分布特点，说明数据中存在不止一个数据量级差异。对图4 中按伤亡人数排序的数据进行函数拟合，得到的拟合结果如图6 所示。其中，离散分布的点表示数据值，曲线为数据点的拟合函数曲线。

图4 按伤亡人数排序后的结果Fig.4 Results sorted by number of casualties

图5 伤亡人数排序后随机截断结果Fig.5 Random truncation results after ranking of number of casualties

图6 伤亡人数拟合结果Fig.6 Fitting result of number of casualties

由图6 可以看出，该函数曲线在趋近末端时突然升高，这是数据的量级突然改变所致。表2 为图6 中拟合函数的多项式参数设置情况，根据拟合函数曲线计算得到k=4 067.95，截断点x_j=87。从截断点87 对数据进行截断完成第1 次离散，得到的第1 个离散类为排序后的数据88～数据99，剩余数据为数据0～数据87。

表2 图6 中拟合函数的参数设置Table 2 Parameter setting of fitting function in Fig.6

对第1 次数据截断后的剩余数据进行函数拟合，并计算下一个截断点，得到拟合函数曲线如图7所示。可以看出，剩余数据分布差异仍较大，这是隐藏的数据量级差异所致。表3 为图7 中拟合函数的多项式参数设置情况，根据拟合函数曲线计算得到k=228.98，下一个截断点为64。

图7 第1 次截断后剩余数据的拟合结果Fig.7 Fitting result of residual data after the first truncation

表3 图7 中拟合函数的参数设置Table 3 Parameter setting of fitting function in Fig.7

从截断点64 对数据进行截断，得到第2 个离散类，对第2 次数据截断后的剩余数据进行函数拟合，并计算下一个截断点，得到拟合函数曲线如图8 所示。表4 为图8 中拟合函数的多项式参数设置情况，根据拟合函数曲线计算得到k=12.86，下一个截断点为39。

图8 第2 次截断后剩余数据的拟合结果Fig.8 Fitting result of residual data after the second truncation

表4 图8 中拟合函数的参数设置Table 4 Parameter setting of fitting function in Fig.8

从截断点39 对数据进行截断，得到第3 个离散类，对第3 次数据截断后的剩余数据进行函数拟合，并计算下一个截断点，得到拟合函数曲线如图9 所示。表5为图9 中拟合函数的多项式参数设置情况，根据拟合函数曲线计算得到k=3.775，下一个截断点为22。由图9 可以看出，数据从截断点39 截断后，其函数曲线数值分布较均匀，呈现出主要数据的量级差异，进而获得第4 个离散类，截断点为87、64 和39。在不断进行数据截断的过程中，每次截掉的数据都被离散为一个离散点，对离散点赋值后即完成离散。

图9 第3 次截断后剩余数据的拟合结果Fig.9 Fitting result of residual data after the third truncation

表5 图9 中拟合函数的参数设置Table 5 Parameter setting of fitting function in Fig.9

本文将数据离散量作为判定离散完成的指标，设置伤亡人数和灾区受灾人数的离散量为4，其他数据离散量为3。在将离散系数阈值作为判定条件下，当离散系数较低时多量级应急数据产生离散量过多（见2.2 节），实验结果不具有实际指导意义。

2.1.2 突增点的判断

本文离散方法在计算斜率时将导函数的凸函数部分作为突增点，并以地震灾区乡镇数的截断点判断过程为例进行分析，结果如图10 所示（实线为数据的拟合函数曲线）。图10（a）和图10（b）分别为地震灾区乡镇数原始数据拟合结果以及第1 次截断后剩余数据的拟合结果。由图10（b）可以看出，截断点在数据60～数据80 范围内。图10（c）为第2 次截断后剩余数据的拟合结果，可以看出截断后数据图像与图10（b）的计算结果差异较大，说明截断点判断错误。在计算中将凸函数作为突增点是截断点判断错误的原因，若在程序判断中加入“当二阶导函数大于零时：将一阶导函数设置为10 000”，则在判断式（4）计算结果的最小值时就无需考虑因凸函数产生的斜率。对数据截断后的剩余数据进行函数拟合，并计算下一个截断点，拟合结果如图11 所示，可见截断点回到数据60～数据80 范围内，函数曲线上升较平缓，未出现突增现象，截断点判断错误的情况消失。

图10 地震灾区乡镇数截断点判断过程Fig.10 Judgment process of the cut off points of number of towns in earthquake stricken areas

图11 截断点判断错误消失Fig.11 Disappearance of error in judgment of truncation point

2.1.3 离散化结果分析

震发地受灾人数的离散、灾区人口密度数据的离散、震发地人均GDP 数据的离散等其他类型应急数据的多量级离散化结果如图12～图17 所示。其中，图12、图14 和图16 为各类数据未离散时的数据排序，图13、图15 和图17 为各类数据离散后各离散类的数据分布。可以看出，采用本文方法离散后的数据在各离散类数量区间中分布较均匀，无较大的量级差异。为量化这种均匀性，下文从离散系数分析本文方法的必要性与合理性。

图12 受灾人口原始数据Fig.12 Raw data of affected population

图13 受灾人口数据的不同离散类Fig.13 Different discrete categories of affected population data

图14 受灾人口密度原始数据Fig.14 Raw data of affected population density

图15 受灾人口密度数据的不同离散类Fig.15 Different discrete categories of affected population density data

图16 灾区人均GDP 原始数据Fig.16 Raw data of per capita GDP in disaster area

图17 灾区人均GDP 数据的不同离散类Fig.17 Different discrete categories of per capita GDP data in disaster area

2.2 离散系数分析

离散系数又称变异系数，常用于衡量数据的离散程度和变异程度，其表达式为σ/-a（σ为离散标准差，-a为离散平均值）。本文利用该系数衡量各个离散类的数据均匀分布程度，同一个数据集离散系数越低，数据分布越均匀，说明离散效果越好。

2.2.1 确定离散类个数时不同方法的离散系数

本文设定伤亡人数与受灾人数的离散类个数均为4，其他数据的离散类个数为3，计算得到不同数据集经本文方法、层次聚类离散化方法、等频离散化方法、等距离散化方法以及2-Flou 数离散化方法离散后的离散类平均离散系数，其中2-Flou 数离散化方法是基于模糊区间与等距离散化的柔性离散化方法［21］，采用不同方法得到的5 种数据集平均离散系数如表6 所示。

表6 不同方法下5 种数据集的平均离散系数Table 6 Mean values of discrete coefficients of five database with different methods

由表6 可以看出，在5 种数据集中本文方法的离散系数较其他方法有一定程度的降低，仅在灾区人均GDP 数据集中离散系数高于层次聚类离散化方法与等距离散化方法。由于层次聚类与等距离散化方法所得离散系数平均值较高，因此每个离散类包含的数据较少。综合不同数据集的平均离散系数给出各方法的平均离散系数如表7 所示，可以看出本文方法在规定离散类个数下平均离散系数低于其他方法，其各个离散类的数据分布较均匀，证明本文方法具有一定的必要性。

表7 不同方法的平均离散系数Table 7 Average discrete coefficients of different methods

2.2.2 设定离散系数阈值后的离散类特征

从统计学上看，若数据集内离散系数低于0.15，则数据集中的数据分布较均匀，否则认为数据分布异常，可据此设定较低离散系数阈值。使用本文方法对各个大于阈值的离散类继续离散，直到小于规定阈值，并给出两种阈值设定方法以及数据集离散后的离散类个数、平均离散系数等离散类特征。当阈值为0.15 和0.30 时，5 种数据集的离散类特征分布分别如表8 和表9 所示。可以看出，与较高离散系数阈值下的离散结果相比，平均离散系数有所降低，最大的离散类个数达到26，大部分数据离散后的离散类个数超过10。如果99 个数据离散后存在超过10 个离散类时，则在后续粗糙集等数据分析中将难以找到数据的主要特征，此类数据离散化并未降低数据间的复杂性。由于应急数据的量级差异变化较大，离散系数高于0.15 并不表示数据之间关联性差，因此应急数据需通过确定离散类个数进行离散化。由离散类数据、离散类个数与离散类离散系数分析结果可知，本文方法具有一定的合理性。

表8 阈值为0.15 时5 种数据集的离散类特征Table 8 Discrete class characteristics of five datasets at a threshold of 0.15

表9 阈值为0.30 时5 种数据集的离散类特征Table 9 Discrete class characteristics of different datasets at a threshold of 0.30

3 结束语

针对具有多量级差异性的应急数据，本文提出一种无监督的数据离散化方法。将应急数据由大到小排序，在函数拟合的基础上计算量级差异变化点作为数据截断点，对数据进行截断移出较大数据完成一次离散，并不断重复此操作直到完成全部数据离散。实验结果表明，该方法的离散系数较等频离散化、层次聚类离散化等传统方法更低，对隐藏多量级差异的应急数据具有良好的离散效果。后续将针对多种复合环境影响下的地震数据进行研究，进一步降低该方法的离散系数并提高鲁棒性。