基于多软件协同的商用车驾驶室橡胶悬置优化设计
许恩永
(东风柳州汽车有限公司,广西柳州545005)
商用车行驶工况较复杂,多种激励通过传递路径至驾驶室并作用于驾乘人员,影响乘坐舒适性与行驶平顺性[1]。橡胶衬套因其性能稳定、结构简单及易于制造的优点在商用车悬置系统中得以广泛应用[2]。目标长头商用车驾驶室前悬置采用橡胶悬置,影响其舒适性的主要参数为整车坐标系下的x向和z向刚度系数,合理设计悬置系统橡胶衬套特性参数可显著改善驾乘人员舒适性。
针对商用车平顺性优化,文献[3]通过响应面法对优化目标进行拟合,并应用多目标遗传优化算法NSGA-Ⅱ对悬架硬点坐标进行优化,取得明显的优化效果,但通过响应面法建立的模型,并不能准确代替仿真计算模型,此外当影响参数数量庞大时模型建立复杂。文献[4-5]基于牛顿第二定律或拉格朗日方程推导商用车振动微分方程,应用Matlab建立出整车平顺性模型,并通过优化算法对平顺性进行优化,但所建模型较为简单,仅能对驾驶室垂直振动与俯仰振动进行仿真,同时未考虑衬套等部件对整车振动的影响。文献[6]为提升某商用车驾驶室舒适性,对其悬置系统进行仿真隔振试验,并基于全因子试验设计方法对其悬置刚度与阻尼进行优化匹配,得到较为理想的优化结果,但此类优化方法需大量重复仿真计算且优化效率与可靠性取决于因子水平数,水平数过少不能确保得到最优结果,水平数过多会使得计算次数呈指数形式增加,优化效率下降。文献[7]以驾驶室综合加权加速度均方根值为目标函数,前后悬置动挠度为约束条件,利用Isight 软件建立优化平台,应用多岛遗传算法对商用车平顺性进行优化,但建立的仿真模型未考虑车架柔性对整车平顺性计算的影响。文献[8-9]研究表明车架柔性对车辆平顺性评价具有重要影响。
鉴于上述研究现状,本文提出一种基于多软件协同的驾驶室橡胶悬置优化方法,应用Adams 建立长头商用车刚柔耦合多体动力学模型,并基于批处理命令将其同多学科优化软件Isight、数值计算软件Matlab 进行集成以建立多学科优化平台;进一步建立以座椅导轨x向与z向振动加速度频率加权均方根值之和为目标函数、橡胶悬置x向与z向刚度为优化变量的优化模型;应用改进遗传算法(NSGA-II)实现目标函数优化。同传统商用车平顺性模型优化方法相比,本方法能得到可靠性更高的最优解,同时可避免重复设置与求解,提高优化实施人员的工作效率。
1 多体动力学理论与整车建模
1.1 多体动力学理论
Adams 多体动力学软件根据机械系统模型自动建立系统拉格朗日运动方程:

式中:T为多体系统总动能;q为系统广义坐标;Q为系统广义坐标;ρ为系统基于完全约束的拉氏乘子矩阵;μ为系统基于不完全约束的拉氏乘子矩阵。
式(1)简化后为
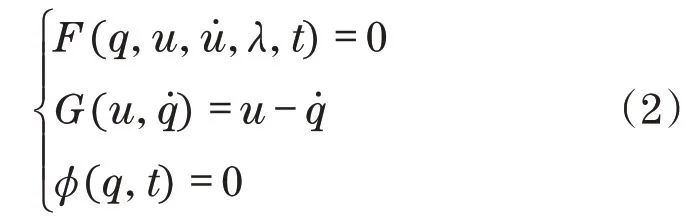
将研究系统变换为零自由度系统方程进行求解。根据机械系统特性不同,动力学微分方程求解时可选择不同的积分算法,但基本可分为预估、校正与求解阶段。预估阶段根据当前时刻系统状态矢量值,用泰勒级数估算下一时刻系统状态矢量值:

式中:h为积分步长。
基于该方法得到下一时刻的系统状态矢量有时不够准确,则用吉尔积分求解程序进行校正:
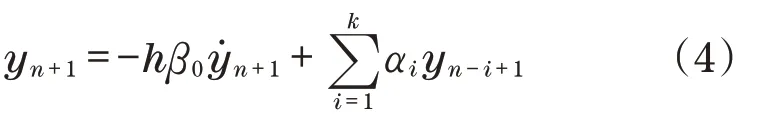
式中:yn+1为y(t)在t=tn+1时刻近似值;β0与αi为吉尔积分程序系数值。
校正阶段主要判断系统方程是否为0,是,则表示预估阶段正确,可进入求解阶段;否,则对y进行更新直到系统方程为0。
1.2 整车多体动力学模型
基于目标长头商用车的实际结构分别建立驾驶室、柔性车架、前后车桥、离散板簧、转向、制动、动力、车轮等子系统,并装配建成整车刚柔耦合多体动力学模型。其中,驾驶室多体动力学模型如图1所示,整车多体动力学模型如图2所示。观察图1与图2 知,目标商用车驾驶室橡胶前悬对整车平顺性与驾驶室舒适性评价具有重要影响,在其车辆设计优化过程应予以重视。

图1 驾驶室多体动力学模型Fig.1 Cabin multibody dynamics model

图2 长头商用车多体动力学模型Fig.2 Multi-body dynamics model of long-head commercial vehicle
2 驾驶室橡胶悬置性能参数优化
2.1 优化变量
目标长头商用车处于开发完善阶段,驾驶后悬置刚度阻尼参数已完成优化调整,故研究主要针对驾驶室前悬橡胶悬置开展,弹性元件比结构件对系统的振动特性影响更显著[10]。综合考虑,选择橡胶悬置x、z向刚度为优化变量,同时基于工作经验,将橡胶悬置原始刚度增大、减小800 N/mm 作为优化区间:

式中:kxl为驾驶室左前悬x向刚度;kxr为驾驶室右前悬x向刚度;kzl为驾驶室左前悬z向刚度;kzr为驾驶室右前悬z向刚度。
2.2 目标函数
参考国标GB/T 4970—2009《汽车平顺性试验方法》,选择驾驶员座椅导轨处x向与z向加速度频率加权均方根值之和作为目标函数:

式中:RMS,x为座椅导轨x向振动加速度频率加权均方根值;RMS,z为座椅导轨z向振动加速度频率加权均方根值。
上述均方根值可通过下式计算:
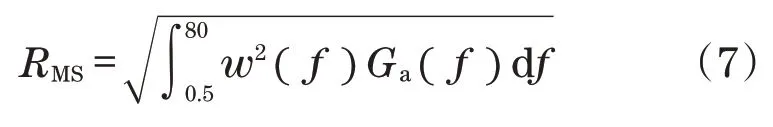
式中:w(f)为频率加权函数。
x向与z向频率加权函数分别为

Ga(f)为对加速度时域信号进行频谱分析得到的功率谱密度函数,方程为

2.3 优化模型
多学科优化平台Isight 拥有强大的开放接口,可同多种主流软件进行集成计算。优化组件通过批处理命令集成Simcode 组件与Matlab 组件,实现优化自动控制仿真驱动与数据读写,应用改进遗传算法实现目标商用车驾驶室悬置衬套优化研究。某步优化流程可简述为:优化算法依据上代优化结果对动力学模型中橡胶悬置刚度属性文件进行修改调整;Simcode 组件驱动多体动力学模型进行平顺性仿真计算;Matlab读取仿真时域结果进行频谱分析以得到功率谱密度,进行频率加权得到加权均方根值;最后计算目标函数并返回给优化算法,以作为下次橡胶悬置特性调整依据。基于以上叙述搭建如图3 所示的多软件协同优化模型,表1 为优化算法,所使用的是相关参数的数值或实施策略。
2.4 优化结果
优化前后驾驶室橡胶悬置x向与z向刚度如表2 所示。优化后橡胶悬置刚度都大弧度降低,为便于计算设置,统一取x向刚度为320 N/mm,z向刚度为160 N/mm。
3 优化前后目标商用车平顺性对比
3.1 随机路面优化前后加速度对比
为确认上文驾驶室橡胶悬置刚度优化对整车平顺性的优化效果,分别建立优化前橡胶悬置刚度属性文件(x向700 N/mm,z向900 N/mm)与优化后橡胶悬置刚度属性文件(900 N/mm,160 N/mm)。将其应用于动力学模型后在随机路面上进行50~90 km/h 车速平顺性仿真计算,车速间隔取10 km/h,仿真界面如图4 所示。以驾驶员座椅导轨的x向、z向振动加速度频率加权均方根值为目标商用车平顺性的评价指标,可得图5 所示的优化前后目标商用车平顺性对比,高车速范围效果明显。
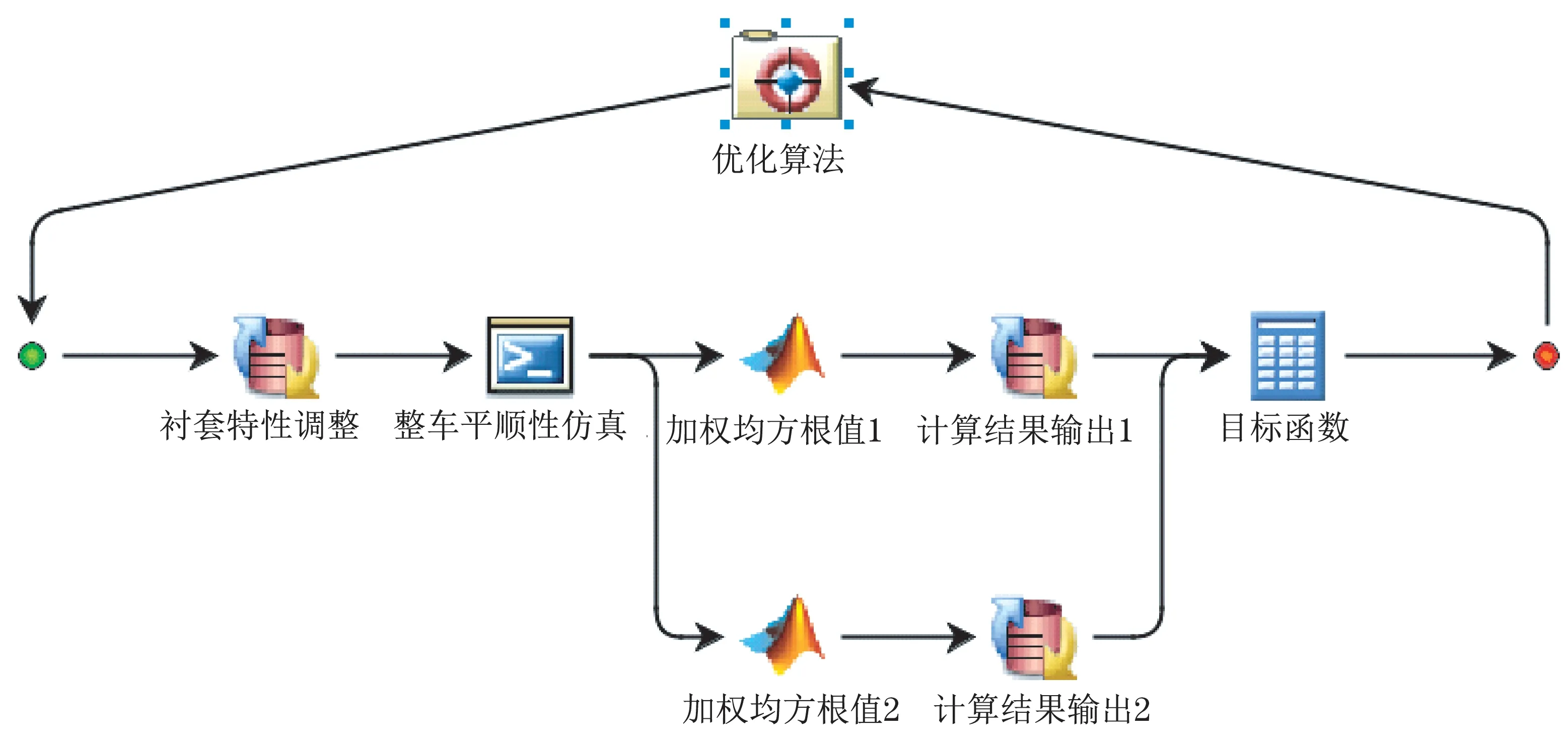
图3 基于多软件协同的优化模型Fig.3 Optimization model based on multi-software collaboration

表1 改进遗传算法相关参数Tab.1 Improved genetic algorithm related parameters
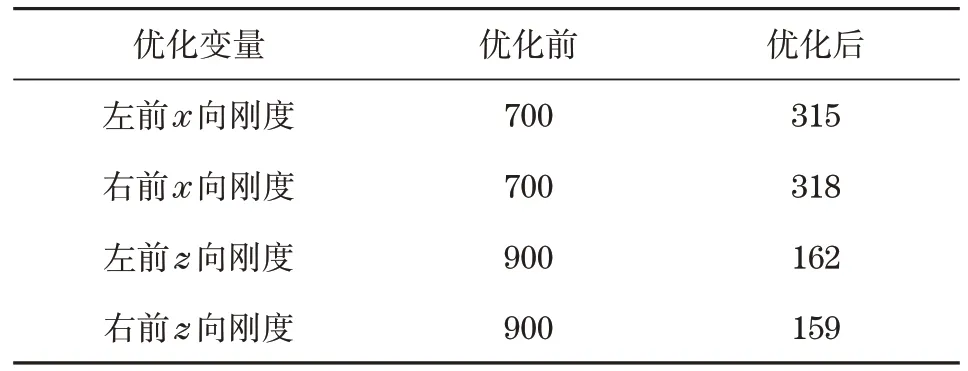
表2 优化前后驾驶室橡胶悬置刚度对比Tab.2 Improved genetic algorithm related parameters N/mm
3.2 冲击路面优化前后加速度对比
为进一步分析橡胶悬置优化对平顺性的提升作用,开展冲击路面下整车平顺性仿真计算,分别进行以 50、60、70、80 和 90 km/h 车速通过冲击凸块,如图6 所示。以驾驶室座椅导轨处x向与z向振动加速度峰值为平顺性评价指标,仿真结果如图7 所示。由图可知,橡胶悬置调整后在冲击路面能大幅度降低振动加速度峰值,5 种车速下x向平顺性平均提升38.4%,z向平顺性平均提升25.5%。

图4 目标车辆通过随机路面Fig.4 Target vehicle passes random road

图5 座椅导轨振动加速度频率加权均方根值Fig.5 Frequency weighted RMS value of seat rail vibration acceleration
4 试验验证
根据优化结果设计出图8 所示橡胶悬置结构,减少橡胶材料增加橡胶运动空间以降低刚度。对优化后的橡胶悬置进行换件试验,测试车辆、测试路面、加速度传感器安装位置、数据采集设备如图9所示。优化前后目标长头商用车满载于水泥高速路面的平顺性测试结果如图10 所示。对比分析可知,优化后目标商用车整体平顺性提升明显,同仿真结果相比具有相似的降低趋势,x向频率加权均方根值平均降低19.9%,z向频率加权均方根值平均降低18.1%,表明上文对橡胶悬置进行优化是有效可行的。

图6 目标车辆通过冲击路面Fig.6 Target vehicle passes bump road
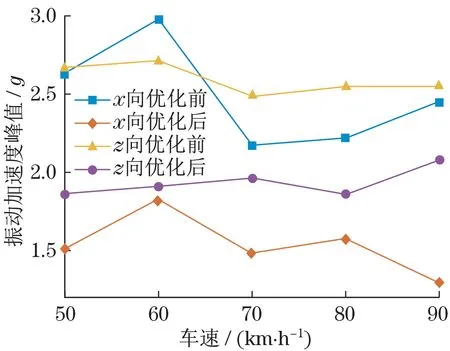
图7 座椅导轨位置振动加速度峰值Fig.7 Peak value of vibration acceleration for driver seat rail

图8 优化后橡胶悬置结构Fig.8 Optimized suspend mount structure

图9 平顺性测试Fig.9 Ride comfort experiment

图10 优化前后频率加权均方根值对比Fig.10 Comparison of frequency weighted RMS values before and after optimization.
5 结语
面向商用车平顺性与驾驶室舒适性优化问题,提出一种基于多学科协同、多软件集成的商用车平顺性优化方法。建立整车刚柔耦合动力学模型,基于批处理命令将之同多学科优化软件Isight 以及数值计算软件Matlab 进行集成以建立优化平台。以橡胶悬置x向与z向刚度为优化变量对平顺性进行优化,基于优化结果开展平顺性仿真对比、试验验证。结果表明:优化后目标商用车平顺性整体提升20%左右,优化方法合理有效,对其他悬置结构优化设计具有借鉴作用。

