基于死区和抗饱和补偿的线控制动系统非线性压力控制研究
熊金凤,陈 伟,任萍丽
(1.常州机电职业技术学院车辆工程学院,江苏常州213164;2.江苏科技大学电子信息学院,江苏镇江212003)
近年来,车辆行业都致力于主动安全、车辆动态控制策略以及自动驾驶。车载执行器能实现这些控制系统的实际应用,其允许设备根据驾驶员的命令独立地或在一定的自由度内调节所需的控制变量。线控制动系统技术专注于执行器的设计,该执行器能够将所需的制动扭矩施加到车轮上。目前的线控制动系统分为两类:电子液压制动系统(EHB)和电子机械制动系统(EMB)[1]。本文研究的一种改进电子液压制动系统,其优点是保留了普通车辆液压制动器布局,仅增加了电动执行器,从而节省了空间、重量和成本。对于这种线控制动系统技术,一方面存在压力/位置非线性中引发特殊的非线性死区效应,另一方面存在输入饱和问题。因此,建立线控制动系统数学模型,研究线控制动系统非线性压力控制具有重要的意义。
文献[2-3]开发了一种以超磁致伸缩材料为驱动源的新型线控制动系统,详细介绍各个组件,同时对系统性能进行试验验证,结果表明该线控制动系统具有优秀的制动效果。文献[4-5]建立了工程车辆线控液压制动系统的数学模型,设计相应的模糊控制器和比例积分微分控制(Proportional Integral Differntiation,PID)控制器。在Simulink和AMESim 中搭建了与实际线控液压制动系统相吻合的仿真模型,仿真结果显示模糊控制响应速度最快,制动效果好。文献[6-7]提出了一种基于PID+PWM控制的液压制动系统,研究电子液压控制系统的工作原理,在AMESim 软件中建立了液压制动系统的仿真模型,利用PID 控制液压系统电机转速,利用脉宽调制系统(Pulse Width Matulation System,PWM)控制高速开关电磁阀,通过仿真验证该控制策略的有效性。以往对线控制动系统的压力控制研究取得了有效的成果,但缺点是如果不能精确识别静态位置压力关系,那么动态闭环性能可能会大大恶化,并显示出较大的超调量。以往研究都没有考虑电动机电流的饱和,本文采用基于死区和抗饱和补偿的PID 控制器对线控制动系统进行控制,优化控制模型,给出面向控制的数学模型。对传统PID 控制器进行改进,添加了死区和抗饱和补偿来增强闭环系统的性能。在Matlab 软件中对线控制动系统进行仿真验证,与传统PID 控制器仿真结果进行对比,为提高线控制动系统控制奠定了理论基础。
1 线控制动系统数学模型
线控制动系统由两部分组成:①由直流电动机组成的机电执行器;②液压制动器,包括液压泵、管道、制动钳、制动块和制动盘。执行器连接到液压泵,通过前后移动活塞,可以调节液压泵主缸中的压力。为了能够实现对主缸中压力的精确控制,同时简化控制模型,这里提出了面向控制的模型。通过在液压泵的主缸上施加力平衡,可以得出一个简单的面向控制的模型为

改写方程(1),得到

式中:v为主缸的速度;k2=Kdamp/m*;k1=Kspring/m*;kp=Amc/m*;ku=Qeq/m*;u为直流电动机的输入电流;y为要调节的压力。
通过将拉普拉斯变换应用于线性分量,得到如图1 所示的线控制动系统控制流程。由于系统存在制动储液槽,活塞位移x在死区范围内,所以输出的压力y为0;而超出死区时,因为流体压缩率变化,活塞位移x与输出压力y便呈非线性关系。同时,如果输入电流u没有限制,会对电子元器件造成较大的损害,影响控制效果。因此,需要设计带死区补偿以及抗饱和补偿的控制对线控制动系统进行有效控制。

图1 线控制动系统控制流程Fig.1 Control flow of the brake-by-wire system
2 死区补偿的控制器设计
这里提出一种控制策略来获得对图1 的非线性线控制动系统的调节。系统模型式(2)以状态空间形式表示为

针对式(3)设计线性误差反馈控制器为
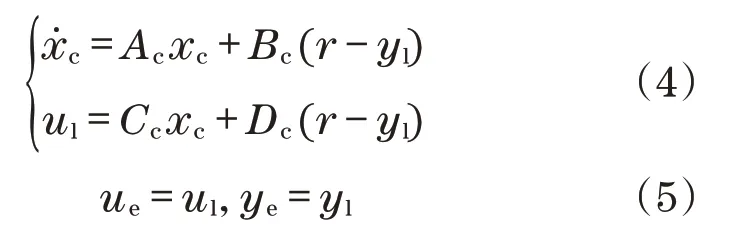
式中:ue为状态空间下的输入电流;ye为状态空间下的调节的压力。
通过线性控制器中的积分作用以诱导零稳态调节误差并抑制方程中的恒定干扰来实现调节特性。
对式(4)代表的线性控制器设计死区补偿方案,如图2 所示。在方案中,死区补偿块在受控对象的输入和输出处注入合适的非线性校正信号:


图2 基于死区补偿的控制器结构图Fig.2 Controller structure diagram based on dead zone compensation
选择的非线性校正信号udc和ydc需要保证ue和ye之间的动力学关系是线性的,同时与式(3)中的目标线性系统一致。为此,使用位置测量值x作为死区补偿模块输入就足够,即

将式(6)代入式(2),得

根据式(9),可得出所需的输出yl=y+ydc的调节特性。由于设定点满足r≥pmin>0,因此,稳定平衡 (xc*,x*,0) 满足p(x*) =pe(x*)。从式(7)开始且渐近调节属性对于实际输出y也成立。因此,对于输入u不带电流饱和极限时,图2的控制方案能够实现本文控制目标。
3 抗饱和补偿的控制器设计
输入电流u过大会对电子元器件造成损伤,因此,需要对输入u进行控制。当输入u受限制时,在式(2)中添加了控制输入饱和,即

式中:σ(u)为控制变量饱和度[12]。
带死区补偿的线性控制器可以视为通用的非线性控制器Knc。存在输入饱和的情况下,修改式(6)、式(7)和式(8)为

(xaw,yaw)来自以下具有状态ξaw=[xawvaw]的抗饱和滤波器:

定义无约束坐标:
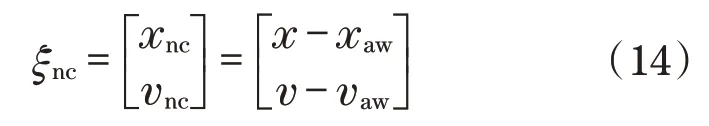
根据式(10)、式(11)和式(12)得到
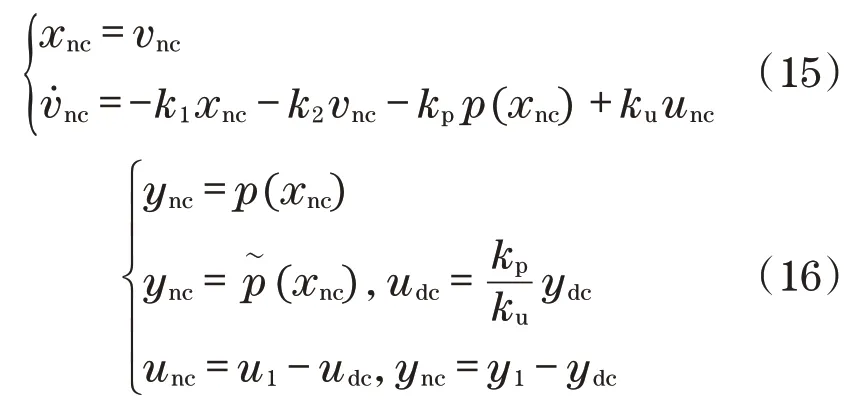
上式与无约束互连式(2)、式(6)、式(7)和式(8)一致,表明无约束控制器Knc实际上以没有饱和状态与非线性被控对象连接,并且与抗饱和补偿器式(12)的反馈互连具有固有的级联结构。
根据式(14)中引入的坐标ξnc和式(15)中的导数,写入坐标(xc,ξnc,ξaw)的整体闭环对应于无约束闭环式(4)和式(15)之间的级联互连,通过信号unc和xnc得到
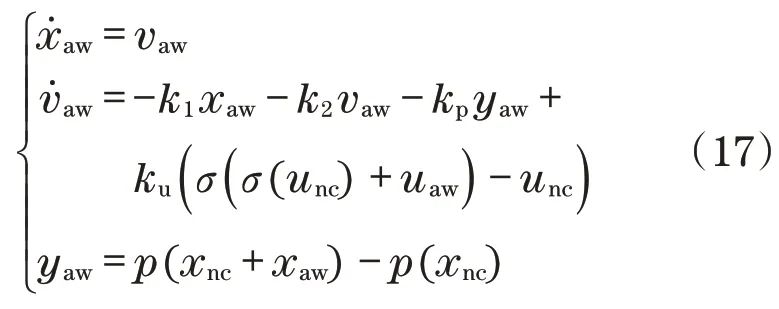

假设存在足够小的ε>0,使得以下方程成立:
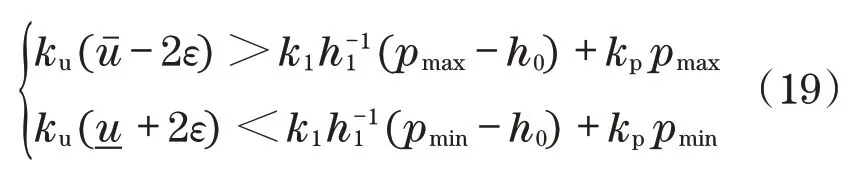
此外,由于unc渐近收敛至满足kuu*=的稳态值u*,从式(19)开始,存在使得对于所有无约束输入unc(t)在集合的内部,且与它的边界至少有一个ε的距离。因此,对于所有可以得到

式中:σε(t,·)是随时间变化的饱和函数。根据式(20)及来自饱和函数的扇区属性,有
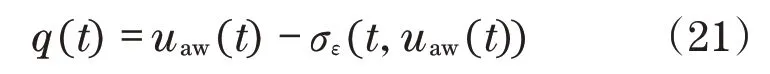
满足

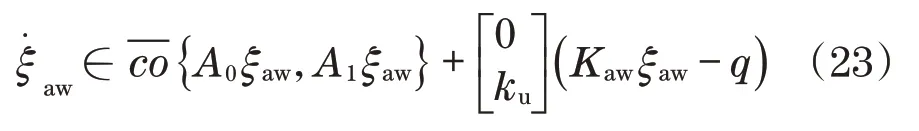

式中:KawQ=X;He(Ξ) =Ξ+ΞT。
最后,矩阵的负性可以通过式(24)的凸组合直接实现。因此,这里所示的方案能够实现本文的控制目标。
4 仿真
为了对比添加死区以及抗饱和补偿的PID控制器与传统PID控制器的控制效果,在Matlab/Simulink环境下,对线控制动系统进行仿真。模型参数设置为:pmin=0.02 MPa,pmax=6 MPa,电流饱和度 ±10 A,k1=50 s-1,k2=25 s-2,kp= 200 mm·s-2/MPa,ku=800 mm·s-2·MPa-1,初始车轮转速30 rad/s,车轮半径0.3 m,车轮转动惯量2.0 kg/m,制动器摩擦因素为0.42,PID参数为Kp=1.8,Ki=0.1,Kd=0.8。期望压力响应曲线为阶跃响应和方波响应,分别表示车辆紧急制动的工况以及车辆突然制动又突然停止制动的工况。期望压力设置为25 MPa,方波信号频率为0.5 Hz。
传统PID 控制以及添加死区及抗饱和补偿的PID 控制下的阶跃响应曲线、方波响应曲线如图3和图4 所示。由图3 及图4 可知,线控制动系统采用传统PID 控制器控制后,具有较大的过冲,波动幅度大,在0.6 s 左右才达到指定值,响应延迟大;而线控制动系统添加死区以及抗饱和补偿后,产生非超调响应,并在0.3 s 左右快速到达指定压力,响应延迟减少约50%。
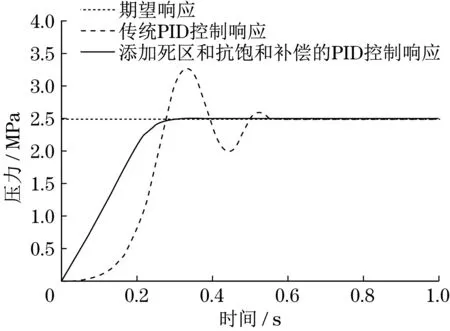
图3 传统PID 控制及添加死区以及抗饱和补偿的PID 控制下的阶跃响应曲线Fig.3 Step response curve under PID controller and PID controller with dead zone and antisaturation compensation
进一步对输入电流进行测试,得到如图5 所示的阶跃响应下传统PID 控制以及添加死区及抗饱和补偿的PID 控制的输入电流变化曲线。图中可见:线控制动系统采用传统PID 控制器控制后,输入电流在0.2 s 后才稳定;而线控制动系统添加死区以及抗饱和补偿后,输入电流在0.08 s 左右就已经稳定,所需的控制工作量大大减少。
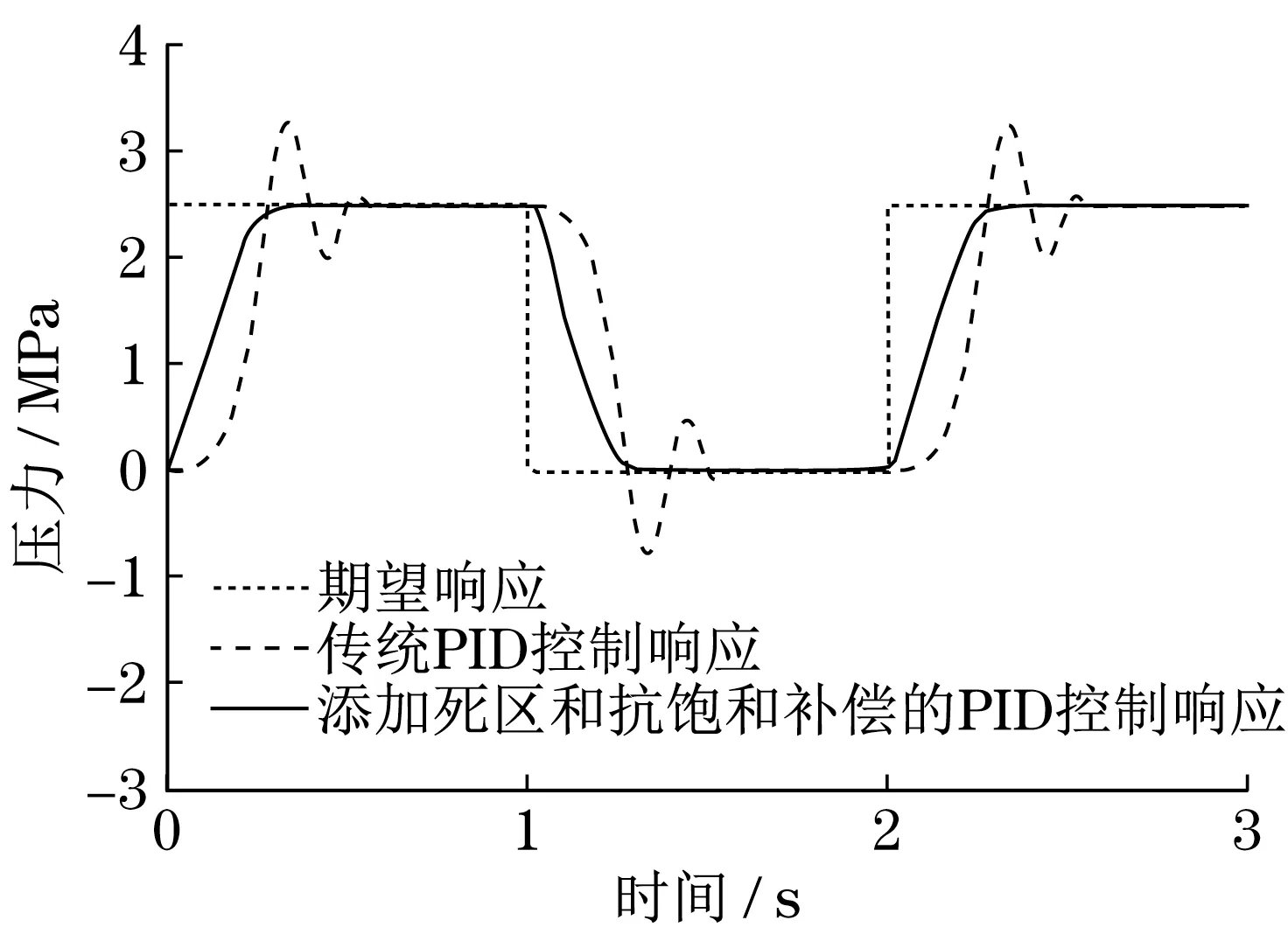
图4 传统PID 控制以及添加死区及抗饱和补偿的PID 控制下方波响应曲线Fig.4 Square wave response curve under PID controller and PID controller with dead zone and anti-saturation compensation

图5 传统PID 控制以及添加死区及抗饱和补偿的PID 控制下输入电流变化曲线Fig.5 Input current curve under PID controller and PID controller with dead zone and antisaturation compensation
对阶跃信号下,传统PID控制以及添加死区及抗饱和补偿的紧急制动轮速变化进行测试,如图6所示。

图6 传统PID 控制以及添加死区及抗饱和补偿的PID 控制下轮速变化曲线Fig.6 Wheel speed curve under PID controller and PID controller with dead zone and antisaturation compensation
图中可见,线控制动系统采用传统PID 控制器控制后,车轮转速在1.9 s 时降为0,在添加死区以及抗饱和补偿后,车轮转速在1.6 s 时就降为0,制动效果显著提高。因此,线控制动系统采用添加死区以及抗饱和补偿的PID 控制器进行控制后,具有较小的跟踪延迟和过冲,跟踪性能明显提高,同时大大减小了获得所需压力的控制量,并且制动效果显著提高。
5 结语
本文优化线控制动系统的数学模型,给出了线控制动系统面向控制的数学模型。对传统PID 控制器进行改进,添加了死区和抗饱和补偿。在Matlab中对线控制动系统响应、控制电流以及车轮转速进行仿真验证,同时与传统PID 控制器仿真结果进行对比和分析。采用基于死区和抗饱和补偿的PID 控制器后,不仅系统响应快,系统控制量也大大减少,并且制动效果显著提高,为线控制动系统非线性压力控制的研究提供了理论依据。

