基于WBS2的一种多维数据多变点检验方法及其应用

毛佳慧，施三支

（长春理工大学 理学院，长春 130022）

变点是指在该时间点上，样本的分布或者数字特征在突然发生变化。研究变点问题可以判断过程中某参数发生变化的时刻并有效控制该参数，也能够分析系统的稳定性，从外部控制变量出发检验或预测形态发生的变化。变点检验就是估计变点的数量和位置，该研究现已广泛用于工业质量控制[1]、医学诊断[2]、交通流[3]和网络安全[4]等许多领域。检验方法也从参数检验发展到非参数检验，检验对象也从一维扩展到多维甚至是高维数据。关于一维数据的多变点问题，许多学者给出了检验效果非常好的方法，如2012年Killick[5]考虑大型数据集的多变点问题，提出PELT法来找到变点可能的数量和位置的成本函数最小值，从而得到具有计算成本的变点的最佳数量和位置，其计算效率是O()n。Rigaill[6]于2015年提出的修剪动态规划将最佳情况下的一些基于惩罚项的变点估计方法的计算耗时加速到线性时间，并提供快速实现。2014年Frick[7]针对指数族回归中的变点提出了控制FWER的SMUCE法。该方法首先最小化α级的一个多尺度检验的接受域上的变点数量，从而估计未知步长函数，再通过构建渐进未知步长函数和变点的置信集，得到估计变点位置的指数界限。Li和 Munk[8]在 2016年提出了基于 FDR的相关方法。Fryzlewicz和 Subba Rao[9]于 2014 年以及 Cho 和 Fryzlewicz[10]于 2012 年利用二元分割对单变量时间序列数据进行分割，Cho和Fryzle⁃wicz[11]于2016年对多变量甚至高维时间序列数据进行分割。2007年Venkatraman和Olshen[12]提出的圆形二元分割，2014 年 Fryzlewicz[13]提 出 的WBS和 2018年 Baranowski等人[14]提出的最窄阈值法旨在提高二元分割的性能。2019年Fryzle⁃wicz[15]在克服了WBS算法缺点的基础上提出了WBS2（Wild Binary Segmentation2），不同于 WBS中所有子分段都是预先分割好的，WBS2算法是数据自适应的，每一组子分段的位置都是由先前检验到的变点的位置决定的，并使用SDLL进行模型选择。关于高维数据变点检验问题的可用工具较少，并且大多不具有普适性，2019年Fryzlewicz针对英国32个城区的房价指数，利用主成分分析将一个32维、长度为284的数据降维成两组一维数据，再分别进行变点检验。

通过研究交通流多维数据的特点，给出了一种基于线性投影的多维数据变点检验方法，能够同时检验多条线或者多个站点的突变点，并对其变点位置从发生时间进行估计。通过生成阶梯状模拟数据，利用不同的变点检验方法进行对比分析，发现WBS2.SDLL能得到较好的检验结果，由于检测的交通数据具有高度相关性，先采用主成分分析和线性投影将多维数据降为一维数据后，再利用WBS2.SDLL进行变点检验，检验结果同每个站点单独进行多变点检验相比，具有快速准确的效果。再高效地找出交通高峰时间段，并推断其发生的原因。

1 数据降维方法

首先利用主成分分析将分量相关的原随机向量通过正交变换转化成分量不相关的新随机变量。具体步骤如下：

假设进行主成分分析的指标变量有m个：x1,x2,…,xm，共有n个评价对象，第i个评价对象的第j个指标的取值为aij。将各指标aij转换成标准化 指 标

其中i=1,2,…,n;j=1,2,…,m；且

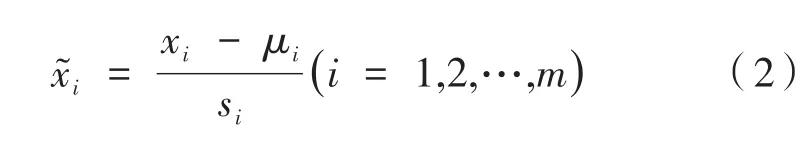
为标准化指标变量。再计算相关系数矩阵R=(rij)m×m：

式中，rii=1；rij=rji；rij是第i个指标与第j个指标的相关系数。再计算相关系数矩阵R的特征值λ1≥λ2≥…≥λm≥0，及对应的特征向量u1,u2,…,um，其中uj=(u1j,u2j,…,umj)T，由特征向量组成m个新的指标变量：

式中，y1是第1主成分；y2是第2主成分，…，ym是第m主成分。再选择p(p≤m)个主成分，计算综合评价值。首先计算特征值λj(j=1,2,…,m)的信息贡献率和累积贡献率。主成分yj的信息贡献率为：

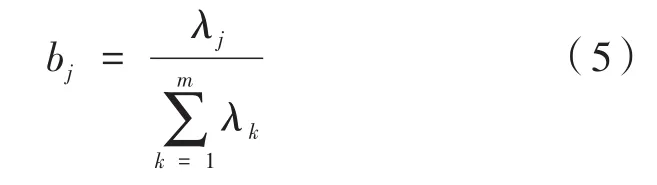
αp为主成分y1,y2,…,yp的累积贡献率：

当αp接近于1(αp=0.85,0.90,0.95 )时，则选择前p个指标变量y1,y2,…,yp作为p个主成分，代替原来m个指标变量。文章提取出累积贡献率达到95%的前三个主成分，再把每个主成分的载荷占三个主成分载荷的和的比例值作为这三个主成分的投影系数，从而能够通过结合主成分分析和线性投影的方法将多维数据降成一维数据。

2 WBS2.SDLL

考虑模型：

其中，ft是一个确定的一维分段持续信号，它的变点数量N和位置η1,…,ηN未知。随机序列是相互独立且服从均值为0且方差为σ2的正态分布，序列是有界的，即对于t=1,…,T，有|ft|0时，δT=δT，间隔长度，满足，故对于一个足够大的常数C，δT和B由要求。Fryzlewicz给出了用于识别候选变点位置的主要定位统计量是累积和，即对于数据(Xs,…,Xe) ：

其中，s≤b≤e，且n=e-s+1。

Fryzlewicz[15]在 2019 年提出了一种递归算法：WBS2。它在第一次遍历数据时，抽取少量M个子区间样本，起点和终点随机选择，并均匀且独立地从集合{1,…,T} 中替换，WBS2将M个CUSUM的绝对值的argmax记为第一个候选变点，然后利用此候选变点将集合{1,…,T} 划分成两个，并再次递归地在候选变点的左侧和右侧抽取M个子区间样本，依此类推，在短子域上所有可能子区间样本将小于M，在这种情况下，WBS2将绘制每个这样的子域的所有子区间样本。

对于检验的置信水平为90%和95%的情况，将两个算法分别称为WBS2.90和WBS2.95。对降维后的一维数据，利用找到(fs,…,fe)中最有可能的一个变点位置。WBS2仅在子域长度为1时停止。完成该步骤后，WBS2按照CUSUM绝对值大小对候选变点进行降序排列。WBS2方案在计算时是数据自适应的，每个下一批M子区间的子域都是由先前检验到的候选变点的位置确定，由于该过程在{1,…,T}不断变短的子域上操作，使得WBS2的计算速度加快，且其只需要设置M这一个参数值。

接下来将对模拟数据进行对比实验，再利用WBS2对降维后的真实数据进行变点检验，相关算法流程图如图1所示。

图1 算法流程图

3 模拟实验与实证分析

先利用多变点检验法PELT、SMUCE和WBS作为对比对象对阶梯状模拟数据进行检验，并从中选出表现最好的方法，再对交通行人流数据进行变点检验。

3.1 模拟计算

使用两组阶梯状模拟数据，其中一组是1 000个带有10个不同均值相同方差的服从正态分布的模拟数据，其均值分别是 1，3，5，7.5，8，6，5，5.5，6，4.5，方差取 1，其数据量均为 100，模拟次数分别为100，200，500和1 000次。第二组模拟数据与第一组的唯一区别是，其数据量是从50，140，120，75，40，160，125，80，60，150中随机无放回地抽取。模拟次数分别是500和1 000。

令N是数据集的真实变点数量，̂是使用算法估计变点数量，则表示变点估计数量的绝对平均值，它与估计的变点位置的许多精度测量值强烈相关。令̂为一个分段常数函数，其每对连续估计变点之间的值是这对变点界定的区间内的数据的平均值。令为模拟中估计ft的均方误差，作为变点位置估计误差的度量。选用作为变点估计的准确率的评价标准，T表示模拟次数，模拟结果如表1、表2和表3所示。

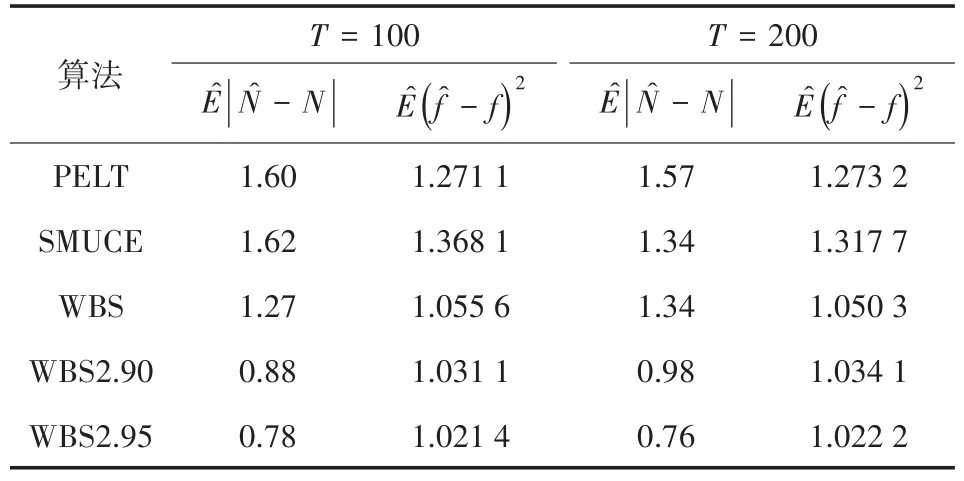
表1 多维数据变点检验模拟结果1

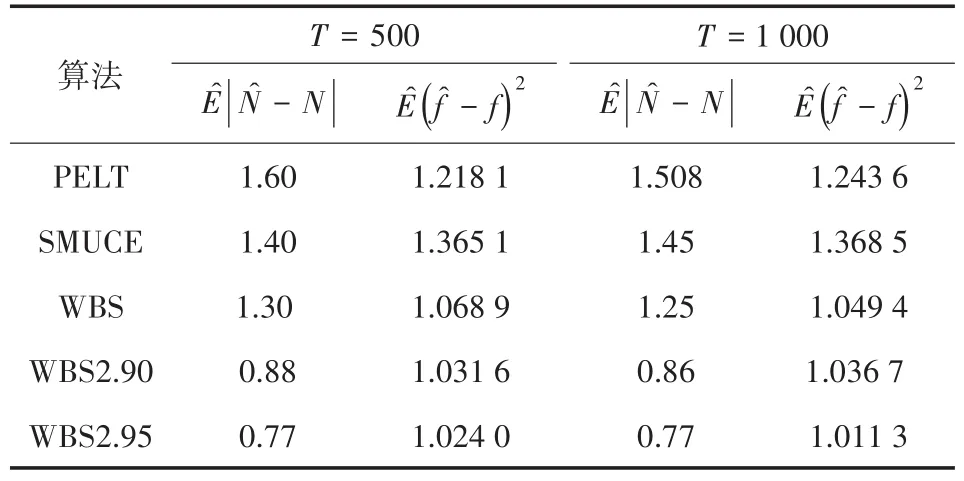
表2 多维数据变点检验模拟结果2

表3 各组数据量不等时数据变点检验模拟结果

表1和表2在第一组模拟数据的基础上得到上述结果，而表3使用的是第二组模拟数据，仅考虑模拟次数分别为500和1 000的情况。由表中结果可知，利用WBS2.95做变点检验得到的变点数量和变点位置的偏差都是最小的，而随着模拟次数的增加误差逐渐越来越小。第二组数据的检验误差相较于第一组的要大，说明随机抽取间隔数使得其中某几组的数据量偏小，会直接影响检验的准确率。

为了更直观地展示检验结果和所用算法的优劣性，以随机产生的其中一组模拟数据为例，将数据和利用不同算法检验得到的变点个数和位置绘制在图2中。

图2 不同算法得到的变点个数和位置

图2从上至下使用的变点检验方法分别是WBS2.95，WBS2.90，WBS，PELT和 SMUCE 法。实线表示其中一个含有10组服从不同均值相同方差的正态分布，且数据量均为100的模拟数据集，竖直的虚线表示算法检验出的变点位置。

图2中使用的模拟数据集的真实变点个数为 9，变点位置分别是 100，200，300，400，500，600，700，800和900。由图2中的竖直虚线的个数和位置可知使用的5个方法中只有WBS2.95法检验得到的变点个数为9，其他方法得到的变点个数均为8，尽管利用五个方法检验得到的变点位置与实际变点位置均有一定的偏差，但是WBS2.95法的偏差相对较小。通过图2与表1和表2的对比结果，采用WBS2.95法对降维后的地铁进出闸机口行人流数据进行变点检验。

3.2 实证分析

选取2015年4月1日上海市地铁一号线上25个站点（富锦路，友谊西路，宝安公路，共富新村，呼兰路，通河新村，共康路，彭浦新村，汶水路，上海马戏城，延长路中山北路，上海火车站，汉中路，新阐路，人民广场，黄陂南路，陕西南路，常熟路，衡山路徐家汇，上海体育馆，漕宝路，上海南站，锦江乐园）的闸机进出口的行人流数据，每五分钟作为一个计数节点。为保证各维度数据量一致，且通过检验发现每天6：30之前和22：00之后地铁闸机进出口的人数较少，不影响之后的检验结果，故将行人流数据的时间段截取为6：20-22：00，从而得到一个25维长度为188的数据集。通过运用主成分分析和线性投影将多维的数据降成1维数据后，再利用WBS2.SDLL对地铁闸机口进站和出站的人数进行变点检验，得到行人进出的高峰期，通过算法检验得到高峰时间段的行人流均值如表4所示。

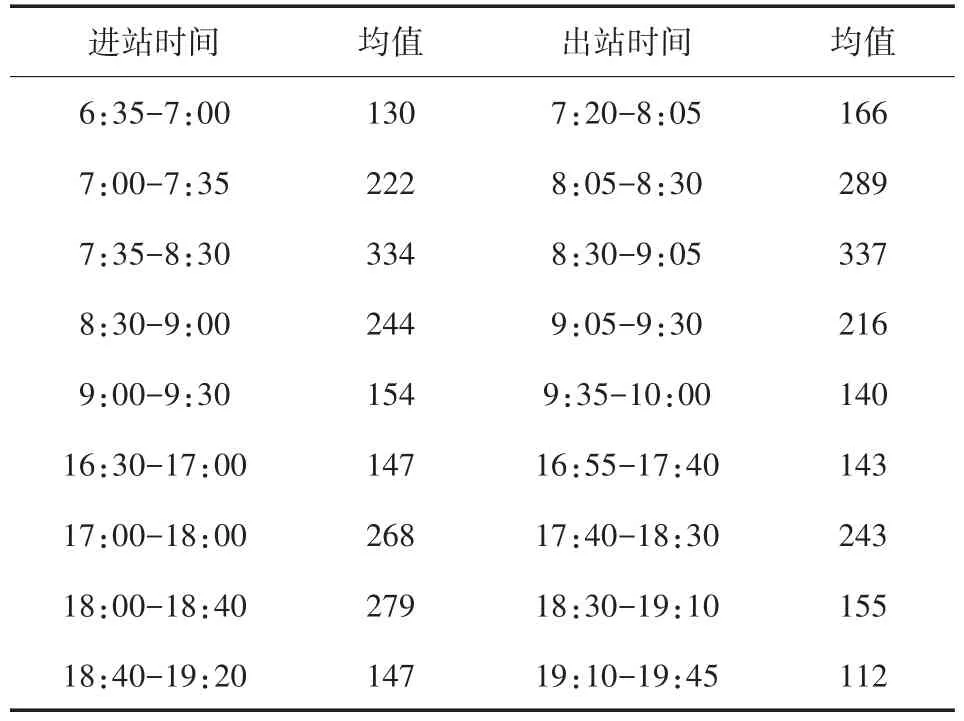
表4 多个闸机进出口高峰时间段

由表4可看出在时间段7：00-9：00和17：30-18：00内，进站闸机口人流量达到最高峰，在时间段 8：05-9：30和 17：40-18：30内，出站闸机口人流量达到最高峰。结合实际与人们通勤时间相符合。同时，为验证上述结果的可信度，接下来将对单个站点闸机进出口行人流进行变点检验，选取一号线中的一个换乘站：汉中路站（可换乘12和13线）作为表4中变点检验结果的对比验证对象，结果如表5所示。

表5 汉中路站闸机进出口高峰时间段

由表5可看出在时间段8：00-8：30和17：20-18：00内，汉口站进站闸机口人流量达到最高峰，在时间段8：30-9：00内，该出站闸机口人流量达到最高峰。上述时间段均被涵盖于多个站点检验得出的高峰时间段内，说明通过结合主成分分析和线性投影来将数据进行降维，再对降维后的数据进行变点检验的方法对地铁行人流数据是有效的，检验结果也是可信的。

通过对上海市一号线25个地铁站的闸机进出口行人数量的变点检验分析研究，根据算法可以计算出行人流发生突变的次数和突变发生的具体时间，从而给交通管理部门对特定时间段的进出闸机口数量的合理开放提供相关数据支持。

4 结论

首先对大量阶梯状的模拟数据利用不同的的多变点检验算法进行变点估计，得到表现较好的WBS2.95。再利用主成分分析和线性投影将一个25维的上海市一号线地铁站闸机进口的行人流数据有效地降成一维数据，再利用WBS2.95进行变点检验，结果表明7：00-8：30和17：20-19：00为进站高峰期，其中 7：46-8：20人流量最大，8：05-9：00和 17：45-20：45为出站高峰期，其中18：15-18：55人流量最大。

将WBS2.SDLL方法运用到行人交通枢纽中，同时考虑多个站点行人流的变点问题，为深入研究多个站点或多条线上的行人流突变问题提供一种新方法，但是WBS2.SDLL只适用于一维数据，之后还将尝试研究一种不需要事先进行数据降维就能够直接用于检验多维数据的方法，为多维甚至高维数据的变点检验问题提供参考。