问题驱动与思想挖掘：“可积条件”教学示范课的个案研究

沈 威

问题驱动与思想挖掘：“可积条件”教学示范课的个案研究

沈 威

（惠州学院 数学与统计学院，广东 惠州 516007）

新时代需要一支高素质、专业化、创新型数学教师队伍，重视数学师范生数学专业课程教学的实践与研究是重要支撑．以面向数学师范生教授的“可积条件”教学示范课为个案，采用质的研究方法探究其教学特征，发现：问题驱动课堂教学与突出数学思想性是该教学示范课的教学特征．

问题驱动；数学思想；数学素养；师范生

1 背景 问题 方法

1.1 背景

百年大计，教育为本；教育大计，教师为本．为此，中共中央国务院印发了《关于全面深化新时代教师队伍建设改革的意见》[1]，教育部印发了《教育部关于实施卓越教师培养计划2.0的意见》[2]，体现国家深刻认识到教师队伍建设的重要意义，要求大力振兴教师教育，不断提升教师专业素质能力．《普通高中数学课程标准（2017年版）》坚持“立德树人”根本任务，把培养学生数学核心素养作为培养目标的核心，并要求以发展学生数学核心素养为导向，制订教学内容、评价标准和教材编制等．受此指导和影响，在中小学阶段开展基于数学核心素养的有关理论研究、教材编写、评价标准研制和教学实践等成为当下热点．培养中小学学生数学核心素养需要一支高素质、专业化、创新型数学教师队伍，数学师范生作为数学教师的后备力量，处于系统接受高等教育培养阶段，在培养师范生数学知识、数学思想、数学素养、数学眼界等具有天然的师资、场所、时间、年龄、精力等优势，加强师范生培养的有关研究与实践具有重要现实意义．

就目前来看，数学师范生的相关研究主要表现为三大主题：（1）数学师范生教学信念研究[3–5]；（2）数学师范生教学知识、教学技能研究[6–11]；（3）数学师范生专业素养研究[12–14]．数学师范生的相关研究主要是问卷与访谈的调查研究或思辨研究，虽然数学师范生学了大量数学专业课程，例如高等代数、数学分析、概率论与数理统计、实变函数、常微分方程等课程，但鲜有对如何在数学专业课程上培养师范生相关知识、能力、思想、眼界等开展行动实践与研究．鉴于数学专业课程对数学系学生的重要意义，有必要对数学专业课程的教学开展研究与实践．

1.2 研究问题

为响应国家对新时代教师队伍建设的重视，提升数学专业课程对数学系学生的培养价值，华南地区H高校数学与大数据学院特邀首届国家级教学名师奖获得者C教授为数学专业课程教师开展教学示范课，教学对象是H高校数学系本科大一学生，使用华东师范大学出版社第四版《数学分析》教材，教学内容是“可积条件”．由于跨校上课和师生课程时间安排等原因，在教学示范课之前两周，已经按照课程教学计划完成“可积条件”的教学，因此，C教授把该教学示范课定位为对已学知识的反思课．将“可积条件”教学示范课作为研究对象，主要研究问题是：“可积条件”的意义、价值与教育性是什么？教师如何揭示研究与学习“可积条件”的真实原因？教师如何引导师范生挖掘“可积条件”的深刻思想内涵与科学意义？

1.3 研究方法与过程

从研究问题可以看出，研究包含对“可积条件”内容及其蕴含数学思想的理解，画出“可积条件”教学过程路线图，对“可积条件”教学过程中所提问题、师生互动等进行宏观把握，并作意义阐释和解释性理解，对教学过程作深描与诠释，归纳“可积条件”教学过程表现的教学特征等，属于自下而上的建构过程，决定了要采用质的研究方法开展研究．

首先征得有关单位和C教授同意，进入教学现场并录制视频，把“可积条件”教学视频转录为文字誊录稿，结合《数学分析》教材、文献和教学过程文字誊录稿，研究分析“可积条件”的知识关系及其蕴含的数学思想，为研究“可积条件”教学案例提供直接基础，而后对“可积条件”教学过程作特征分析和模型建构．因此，研究是一个循环往复的动态过程，在研读教学誊录稿、查阅文献、编码、特征分析、模型建构过程中来回穿梭，螺旋式前进，抽象与概括，并理论化的过程．

2 “可积条件”的数学思想与教育性

2.1 “可积条件”的数学思想

“可积条件”是定积分概念的后续内容，在定积分概念和牛顿—莱布尼茨公式之后学习．定积分是因解决求变力做功、旋转曲面面积、曲线弧长、旋转体体积等问题需要而产生，与数列极限和函数极限的本质相同，即定积分的代数和式与某一定数的距离能变得并保持任意小，体现了定积分蕴含的极限思想；此外，定积分又是一种特殊极限，是解决求总和问题的数学模型，把定义域通过无限细分化整为零，并把每个细分相加，得到总量的近似值，取极限后，得到总量的精确值，蕴含着整体与局部、近似与精确的辩证法思想．

到近代17世纪，牛顿与莱布尼兹提出的微积分基本定理揭示了微分与积分的内在关系，使得数学从常量数学发展到变量数学．当把定积分作为新概念和解决问题的新工具时，首先要从逻辑学的角度研究定积分的内涵与外延分别是什么，而后再从实用角度开展研究．即判断哪些函数可以求定积分，哪些函数不能求定积分，换句话说，可积函数应该满足什么必要条件？满足什么条件的函数才可积？即可积函数的必要条件是什么？充要条件是什么？在满足充要条件的前提下，还需要深入研究函数可积的充分条件是什么？这是驱动研究与学习“可积条件”内容的本原性问题，由此得到了函数可积的必要条件、充要条件和充分条件．在教材中，它们分别是：

函数可积的必要条件（定理9.2）：若函数在[,]上可积，则在[,]上必有界；

函数可积的充要条件（定理9.3）：函数在[,]上可积的充要条件是，任给>0，总存在相应的一个分割，使得()-()<；

函数可积的充分条件（定理9.4—定理9.6）：若为[,]上的连续函数，则在[,]上可积；若是区间[,]上只有有限个间断点的有界函数，则在[,]上可积；若是[,]上的单调函数，则在[,]上可积.

2.2 “可积条件”的教育性

“可积条件”内容蕴含的丰富数学思想决定了其较强的教育性，主要表现在培养学生反思能力、探索能力与创新能力等3个方面．

“可积条件”为培养学生反思能力提供充分内容．例如，本原性问题“函数应该满足什么条件才可积”驱动学生返回到定积分定义中思考，把定积分相关内容与该问题有机结合，从多个维度研究解决问题需要建构的数学定义、公式与定理等，充分运用反身联想、反身观察、反身质疑、反身归纳、反身概括和反身抽象等多种反思性思维操作，逐渐获得函数可积的必要条件（定理9.2）、充要条件（定理9.3）与充分条件（定理9.4—定理9.6）．

“可积条件”的问题解决为培养学生探索性能力提供过程．学生数学学习过程是数学知识的“再创造”过程，要经历发现问题、提出假设、验证猜想的阶段，这些阶段既相对独立又相互渗透，充满不确定性，表现出学生数学思维的探索性特征．例如，学生探究“可积条件”本原性问题时，要根据自己的经验和知识，运用观察、想象、直觉、类比、归纳、验证和反驳等思维动作，对处理的内容作多重信息整合，经历合情推理过程，寻求一种可能性的结论．学生经历解决“可积条件”本原性问题的探索性过程，得到探索性经验与体验将深植于学生的数学认知结构并形成相应的图式结构，为以后解决数学问题提供能有效迁移的探索性思维能力．

“可积条件”为培养学生创新能力提供机会．当学生根据“可积条件”本原性问题来运用反思性思维操作，并经历问题解决的探索性过程而创造性建构“可积条件”的相关定理时，其“再创造”的这些新定理都凝聚着创造性劳动，表现出勇于创造的精神，逐渐培养学生的创新能力．学生只有经历“再创造”过程，主动建构相关定理，揭示定理之间的关系结构，这些定理及其关系结构才能在学生的数学认知结构中真正生成，与学生数学认知结构中原有知识建立非人为本质性的联系，也唯有如此，学生才能真正理解与掌握“可积条件”．

3 研究发现

教学过程路线图能从宏观角度直观展示教学过程中的教学环节、问题结构、互动关系等，能使研究者透过复杂的教学过程，提纲挈领地把握教学过程的“骨架”，理解“骨架”与教学细节之间的关系与意义．“可积条件”教学过程路线图如图1．

图1 “可积条件”教学过程

3.1 以问题驱动为中心的教学结构

从“可积条件”教学过程路线图看，整个教学过程分为3个环节：第一环节是教师引导学生提出问题；第二环节是教师引导学生探究学生所提问题；第三环节是教师引导学生探究教师提出的预设问题．3个环节均围绕“问题”展开，既有学生提出的问题，也有教师提出的问题，且教师引导学生提出问题在先，教师提出问题在后，体现教师对学生学情和教学设计本质有充分的认识，如果教师提出问题在先，把有价值有意义的问题提完了，学生就不再去思考能提出什么问题，以及如何提出有价值的问题，这无益于培养学生提出问题的意识和能力．

先由学生运用已有数学知识和思想方法不断尝试提出问题，再由教师把学生尚未提出的高质量问题提出来，既是对学生提出问题的有效补充，向学生展示还能如何提出更加全面和高质量的问题，且引导学生探究问题蕴含的数学思想方法．前两个环节把时间和机会充分交给学生，让其充分发挥，属于弹性教学设计，第三个环节是教师提出预设问题，属于刚性教学设计，确保在学生无法提出有效问题的情况下，还能使其在问题的驱动下开展数学学习．从教师提出的7个问题看，第一个问题是导向研究与学习“可积条件”的宏观本原性问题，在此基础上不断地演进与细化出后面6个问题，引导学生认识与体验了“可积条件”教材内容背后的“活”的思考过程．可见，“可积条件”教学过程表现出以问题驱动为中心的教学结构．

3.2 以揭示数学探索性特征为重点的教学导向

教师引导学生提出问题、教师自己提出问题、师生共同解决问题是对“可积条件”新内容由“不知”到“知”的科学研究过程，也是发明发现的创造性过程．教师引导学生根据已有知识创造性地分析与研究“定积分”相关概念、性质及其变中不变的性质等，从中提出促使“可积条件”相关定义、性质、定理等产生的本原性问题，这是以问题为载体引导学生经历数学探索性的过程，揭示了数学的探索性特征．

爱因斯坦指出，“提出一个问题，比解决一个问题更重要”[15]，哈尔莫斯说，“问题是数学的心脏”[16]，中国学生不善于提出问题是众所周知的现象[17]，因此，教师引导学生提出的5个问题就意义非凡，需要学生既要把握自己认知结构中已有的知识和思想方法，还需要有效运用数学直觉、数学想象、数学思想方法、思维动作等多方面因素，经过分析与综合、聚焦与发散等思维过程，形成新的数学问题．部分问题的质量非常高，例如问题3“在定理9.2的证明当中，用的是反证法，用反证法时要往哪方面去想？即证明的技巧是如何想到的？”，问题5“针对定理9.5，若是区间[,]上只有有限个间断点的有界函数，则在[,]上可积，如果这个函数有无限个间断点的话，在[,]上可积还是不可积呢？”提出问题3需要学生不仅对定理9.2的证明过程要有本质的把握，还需要思考反证法的一般性以及证明技巧的特殊性，问题5则是导致实变函数产生的本原性问题．

教师提出的7个问题依然意义非凡，中国学生不善于提出问题与教师在课堂教学上不提出问题直接相关，或者说教师在课堂教学中不提出问题是导致中国学生不善于提出问题的直接原因之一．教师提出的7个问题揭示了为何要研究与学习“可积条件”的根本原因，以及在此基础上不断演进研究的思想过程．例如，教师在提出问题2之后，进一步启发引导学生“连续函数是否可积？连续函数为什么可积？如果不连续呢，恰当的条件是什么？如何合理地降低函数的连续性要求？不连续就意味着有间断点，如何考察有间断点的函数？合适的观察点是什么？”．教师不但为学生揭示了为何要研究与学习“可积条件”，为什么会出现某个概念、为了解决什么问题的思想过程，更是向学生展现如何提出有价值、有方向问题的方法论，教学生如何提出问题．这些问题承载的就是数学的探索性特征．

3.3 以挖掘数学思想为焦点的细节阐释

日常教学中经常听到学生反映“老师您讲的我都能听懂，但是我自己就是想不出来，您是如何想到的”，这说明教师没有把解决问题的过程性思想方法交给学生，仅仅告诉学生一个结果而已．在“可积条件”教学示范课中，提出问题之后，是把结果直接告诉学生还是把解决问题的思想通过细节阐释以培养其自主思考能力？通过课堂观察看出教师选择了后者．从解决问题过程看，以教师引导学生探究他们提出的问题3为例，分析教师如何挖掘与阐释解决问题的数学思想．教师引导学生认识为何要用反证法证明定理9.2，并把反证法中需要假设的结论设为“在[,]上无界”作进一步分析，抓住无界的定义，对其形式转换，用更加具体的数学表达式刻画抽象的“在[,]上无界”，同时以问题的形式启发与引导学生体会反证法证明定理9.2的数学思想．

教师引导过程为：有界性的证明用反证法，这个定理证明最关键的地方是哪里？通常来说，证明是有界的，就假设是无界，无界的意思该怎么表达呢？对于任意的，总能找到，使得|()|>，这是无界的定义．但是这个条件在这个定理的证明中到底发挥了什么作用？是如何发挥作用的？是怎么想到反证法的？有没有同学替他回答这个问题？这对平时解题，或者以后大家当老师引导学生去思考都非常重要，要学会正确的思考问题的方法．大家要搞清楚这个问题的目标是什么，讲的是这个函数如果可积的话，一定是有界的，要把条件和结论之间通过一系列的逻辑关系串起来，最后也许就找得到为什么想到这个办法了．

在启发与引导学生从宏观上认识用反证法证明定理9.2的意义之后，教师便引导学生从反证法的逻辑起点出发，寻找达到反证法证明定理9.2的路线，并逐步揭示反证法前提和结论之间的逻辑关系，即反证命题，应该证明前提不蕴含结论．教师把反证定理9.2分为4个步骤，先揭示证明的4个步骤，在展示过程中不断总结4个步骤，不断启发与引导学生认识与体验用反证法时要往哪方面去想，证明技巧是如何想到的，揭示蕴含在反证法中的数学思想．

3.4 教学特征模型

对“可积条件”教学过程进行解构、重构与特征分析发现，其表现出两方面的特征：数学问题驱动和数学思想挖掘．其中数学问题是“骨架”，撑起这节课的高度，数学思想既是形成“骨架”的成分，又是附着在“骨架”上的“肉”，渗透在整节课中．图2刻画了“可积条件”教学特征的模型．

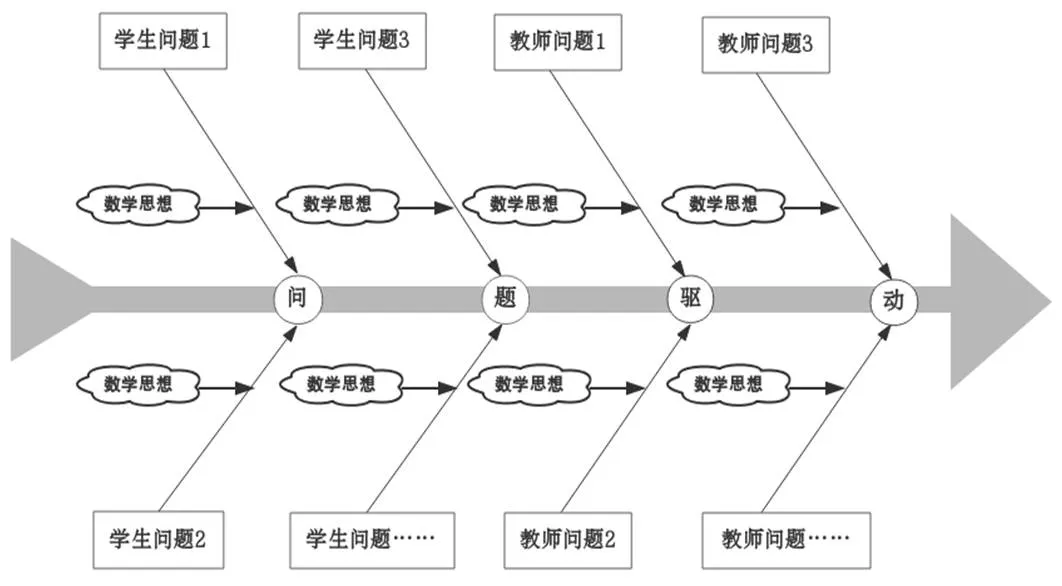
图2 “可积条件”教学特征模型

4 结论

通过研究可以看到，教师把教学过程分为3个环节，引导学生围绕“可积条件”是如何产生的，源于什么样的背景，解决了什么样的问题等提出问题，以问题驱动教学，把教学过程当成科研过程，深挖解决问题背后的数学思想并揭示给学生．教师引导学生发现问题以及对问题的深入分析与解决，像数学家那样思考，完成数学的“再创造”过程，建立函数可积的必要条件、充要条件和充分条件，通过这个过程培养学生善于观察各种现象并透过这些现象发现有规律性内容的能力，进而培养它们发现问题的洞察力、分析问题的思辨力和解决问题的推演力，也就培养了学生的创新能力．

5 讨论

5.1 数学专业课程需要创造性的教学

“可积条件”教学示范课表现出数学教学的创造性，体现了弗赖登塔尔的数学教学“再创造”思想，说明数学专业课可以开展创造性的教学．只有教师创造性地教，才有学生创造性地学；只有教师在教学过程中提出数学知识形成的本原性问题，鼓励与引导学生创造性提出问题，才能培养学生提出问题的意识与能力；只有在教学过程中渗透与揭示数学思想方法，才能培养学生数学思维能力；换句话说，只有把数学问题驱动与数学思想挖掘有机融合，才能培养学生的数学思维能力，也就是培养学生学会思考的能力．从国家对新时代教师队伍建设的要求看，培养中小学学生数学核心素养、数学思维能力等，需要师范生将来具有较高的数学知识、数学思维、数学眼界、数学思想等数学素养，否则，很难想象没有较高数学素养的数学教师能够有效培养学生的数学核心素养．从这个角度看，师范生的数学专业课程迫切需要创造性教学．

5.2 数学专业课具有开展创造性教学的条件

从问题驱动与数学思想挖掘的角度开展创造性教学需要充足时间，而中小学阶段的数学教学受到中考与高考的直接影响，导致部分教师认为没有充足时间开展创造性的教学，或者由于在职数学教师在作为师范生期间缺乏足够数学素养的培养，不知如何开展创造性教学．但是，在高校对师范生开展数学专业课程创造性教学是可行的，高校数学教师考核受到数学师范生考试成绩的影响较小，且具备一定的数学研究经验，受到较为专业的数学研究训练，能够从数学研究的高度，把数学教学过程当做科研过程，按照数学知识形成的本来面目，开展数学问题驱动与数学思想渗透，逐步培养师范生的数学素养．

5.3 加强数学专业课程教学研究

目前的数学教育研究主要集中在中小学阶段，开展高校师范生数学专业课程教学的相关研究比较匮乏．从培养中小学生数学核心素养的角度看，师范生的数学专业课程需要创造性地教，且具备开展创造性教学的条件，因此，加强师范生数学专业课程教学研究就显得迫切了．

[1] 中华人民共和国教育部．中共中央国务院关于全面深化新时代教师队伍建设改革的意见[EB/OL]．（2018–01–31）[2019–09–25]．http://www.moe.gov.cn/jyb_xwfb/moe_1946/fj_2018/201801/t20180131_326148.html．

[2] 中华人民共和国教育部．教育部关于实施卓越教师培养计划2.0的意见[EB/OL]．（2018–09–30）[2019–09–25]．http://www.moe.gov.cn/srcsite/A10/s7011/201810/t20181010_350998.html．

[3] 周仕荣．从数学学习经历看师范生的教学信念发展[J]．数学教育学报，2009，18（4）：84-88．

[4] 张晓贵．对高师数学师范生信念改变的思考[J]．数学教育学报，2010，19（2）：15-18．

[5] 郭桂蓉．数学系师范生在教育实习中对教师身份的理解[J]．数学教育学报，2014，23（5）：91-94．

[6] 李渺．高师数学专业师范生课堂教学技能的调查研究[J]．数学教育学报，2009，18（1）：37-40．

[7] 李渺．数学专业师范生MPCK发展“五部曲”[J]．数学教育学报，2013，22（1）：23-26．

[8] 张锐．数学师范生教学实践性知识的形成和发展研究[J]．数学教育学报，2016，25（1）：80-83．

[9] 王传利．数学职前教师细节实践性知识形成的叙事研究[J]．数学教育学报，2017，26（1）：88-93．

[10] 章勤琼．师范生数学教学知识的实证研究[J]．数学教育学报，2014，23（4）：26-30．

[11] 徐章韬．师范生课程与内容的知识之调查研究[J]．数学教育学报，2014，23（2）：1-5．

[12] 彭光明．地方民族师院数学师范生核心素养的培养模式研究[J]．数学教育学报，2017，26（5）：99-102．

[13] 杨承根．免费师范生数学专业素质的调查研究[J]．数学教育学报，2012，21（1）：65-67．

[14] 刘喆．数学师范生数学素养现状的调查研究[J]．数学教育学报，2012，21（5）：23-28．

[15] 孙正聿．哲学修养十五讲[M]．北京：北京大学出版社，2004：34．

[16] 哈尔莫斯．数学的心脏[J]．弥静，译．数学通报，1982，21（4）：27-30．

[17] 涂荣豹．数学教学设计原理的构建[M]．北京：科学出版社，2018：89．

Problem-Based Instruction and the Development of Thought Processes: A Teaching Case of the Model Lesson on “Integrability Condition”

SHEN Wei

(School of Mathematics and Statistics, Huizhou University, Guangdong Huizhou 516007, China)

The society in the new era calls for highly qualified mathematics teacher educators with professionalism and innovation. These highly qualified mathematics teacher educators can support the education of pre-service teachers and conduct research about the development of pre-service teachers. This paper reports a case study of a model lesson on the topic of the “integrability condition”. It was found that this lesson has two distinctive features: (1) problem-based instruction and (2) the development of thought processes.

problem-driven; mathematical ideas; mathematical literacy; pre-service teachers

G642

A

1004–9894（2021）02–0038–04

沈威．问题驱动与思想挖掘：“可积条件”教学示范课的个案研究[J]．数学教育学报，2021，30（2）：38-41．

2020–10–20

广东省教育科学规划课题——数学教师实践性知识及其教学表现研究（2018GXJK184）

沈威（1982—），男，安徽灵璧人，副教授，博士，主要从事数学课程与教学论研究．

[责任编校：周学智、陈汉君]