基于三角模糊层次分析法的地方院校优势学科评价研究

吴宜涛 潘道远

(1. 安徽工程大学 外国语学院，安徽 芜湖 241000;2. 安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

为加快建成一批世界一流大学和一流学科，到21世纪中叶，把我国建成以支撑创新驱动发展战略、服务经济社会发展为导向的高等教育强国，2015年国家出台《统筹推进世界一流大学和一流学科建设总体方案》.国家鼓励和支持不同类型的高水平大学和学科差别化发展，这将为地方院校的学科建设与发展提供重大战略机遇[1-4].

地方院校由于资源匮乏，存在“重专业、轻学科”的现象.同时，在政府与社会有限资源的投入下，地方院校在学科建设方面基本上是平均主义.为抢抓国家、省部级“双一流”建设的机遇[5]，地方院校如何从现有学科中选择部分学科作为优势学科建设已成为学科建设和管理的难点.在学科评价指标体系方面[6]，主要有教育部学位中心组织的学科评估、广东管理科学研究院组织的《中国大学评价》、中国校友会网发布的《中国大学评价研究报告》、美国科技信息研究所推出的基本科学指标数据库等，上述学科评价指标体系是面向所有学校的所有学科，无法解决地方院校学科区分难的问题.在学科评价方法研究方面，运用系统工程的思想，季淑娟等提出一种基于文献计量的学科评价方法[7]，为有效开展学科评价提供了参考，但该方法尚处于实践研究阶段，无统一的流程标准.从地方院校学科实际出发，郑凌莺等提出一种基于平衡计分卡绩效评估思想[8]，并结合德尔菲法和层次分析法的学科评价方法，该方法易于指标的计算，但存在因人为因素带来主观误差的缺陷.为了提高评价结果的有效性与客观性，针对目前多种评价方法出现评价精度不高的问题，本文提出一种三角模糊层次分析法以用于地方院校优势学科评价.

1 地方院校优势学科评价指标体系

优势学科建设与评价是地方院校的一项紧迫任务，是提升地方院校整体办学水平的战略性措施.将优势学科评价体系作为一个系统，可以划分为不同的层次和指标.根据国家建设地方院校优势学科总体要求和发展方向，并结合各地方院校多年来在学科评价工作中的经验[9]，设计地方院校优势学科评价指标体系如表1所示.由表1可以看出，一级指标包括6个：学科方向、教师队伍、人才培养、科学研究、学术交流、条件建设.每个一级指标又包含若干个二级指标，共计30个.

2 模糊层次分析法的基本理论

2.1 定义及运算法则

定义1：给定论域R上的一个模糊数集是指对任何x∈R，都有一个数μ(x)∈[0,1]与之对应，称为x对R的隶属度，μ(x)称为x的隶属函数.满足式(1)时，称其为一个三角模糊数[10].

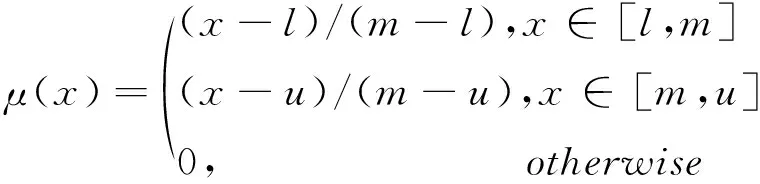
(1)

式中，l≪m≪u，l和u表示模糊程度，u-l越大，模糊程度越高.

表1 地方院校优势学科评价指标

定义2：设M= (l,m,u)、M1= (l1,m1,u1)和M2= (l2,m2,u2)是三角模糊数，其运算法则如下[11]：

kM= (kl,km,kr),k> 0

(2)

M1+M2= (l1+l2,m1+m2,r1+r2)

(3)

M1×M2= (l1×l2,m1×m2,r1×r2)

(4)

M1/M2= (l1/l2,m1/m2,r1/r2)

(5)

定义3：设M= (l,m,u)是三角模糊数，则其去模糊值为[11]：

E=(l+2m+r)/4

根据系统论的观点，教学过程可以看作一个母系统，各个要素是一个个子系统。系统中的各个要素、各个部分只有密切配合，相互协调，始终处于一种和谐状态，才能从整体上提高教学效果，实现教学的最终目的。

(6)

2.2 模糊层次分析法

层次分析法是一种定性和定量相结合的系统化、层次化的分析方法.层次分析法的基本步骤包括：建立层次结构模型、构造成对比较矩阵、计算权向量并做一致性检验、计算组合权向量并做组合一致性检验.为了解决不确定环境下的决策问题，将模糊法与层次分析法的优势结合起来形成了模糊层次分析法.分析影响评价对象的相关因素，建立K层评价指标体系S[12]，其中每层指标个数为P.由N人组成的专家组采用指标体系S对L个评价对象进行评价.设计的三角模糊层次分析法的计算算法步骤如下：

Step 1：建立评价指标体系S，并令i= 1.

Step 2：专家i采用三角模糊数对评价对象的第K层各个指标进行直接描述，并令k=K-1，p=1.

Step 3：令指标体系S中的第k级指标中第p个指标项的所有下一级指标为指标集X.对L个评价对象的指标集X的指标分别进行单因素评价，得到指标集X的评价矩阵G.

Step 4：将指标集X中指标两两比较，得到模糊互补判断矩阵P，然后计算模糊一致矩阵M，求出M的最大特征值及特征向量，并进行归一化处理，得到归一化的特征向量，即指标集X的权重矩阵H.

Step 5：将指标集X的评价矩阵G与权重矩阵H进行模糊运算G×H，得到L个评价对象指标集X的三角模糊数.

Step 6：令p=p+1.如果p=N，执行Step 7；否则执行Step 2.

Step 7：令k=k-1.如果k=1，执行Step 8；否则执行Step 2.

Step 8：令i=i+1.如果i=N，执行Step 1；否则执行Step 9.

Step 9：对N个专家给出的三角模糊数求均值，然后进行去模糊值得到L个对象的评价值T.

专家对评价对象的指标进行直接描述时所采用的评价语言变量与三角模糊数的对应关系如图1所示.由图1可知，评价语言变量不及格、及格、中、良好、优秀的三角模糊数分别为(0, 0, 0.25)、(0, 0.25, 0.50)、(0.25, 0.50, 0.75)、(0.50, 0.75, 1)、(0.75, 1, 1).

图1 三角模糊数的评价语言

3 地方院校优势学科评价实例分析

安徽工程大学是一所以工为主的省属重点建设院校.现有6个省级重点学科：机械制造及其自动化、设计艺术学、检测技术与自动化装置、发酵工程、管理科学与工程、纺织工程.上述重点学科对应的一级学科分别为机械工程、设计学、控制科学与工程、轻工技术与工程、管理科学与工程、纺织科学与工程.学校为了响应国家一流学科建设,将从6个一级学科中选拔3个一级学科作为优势学科培育[13].为了更好地提升学科建设水平，本文采用三角模糊层次分析法对该校6个一级学科进行评价.专家组由11人组成，考虑到评价的客观性，随机从专家库里选择省外地方院校、省内院校、校内的评估专家分别为4人、4人、3人.评价采用表1的指标体系，关键步骤如下：

(1)对各二级指标分别进行单因素评价.例如：专家2对6个一级学科的一级指标A3下5个二级指标进行直接描述，得到的评价矩阵为

(2)专家2对一级指标A3下5个二级指标两两比较[11]，得到的模糊互补判断矩阵为

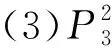
同理，可以得到11位专家给出的所有一级指标下二级指标权重值如图2所示.

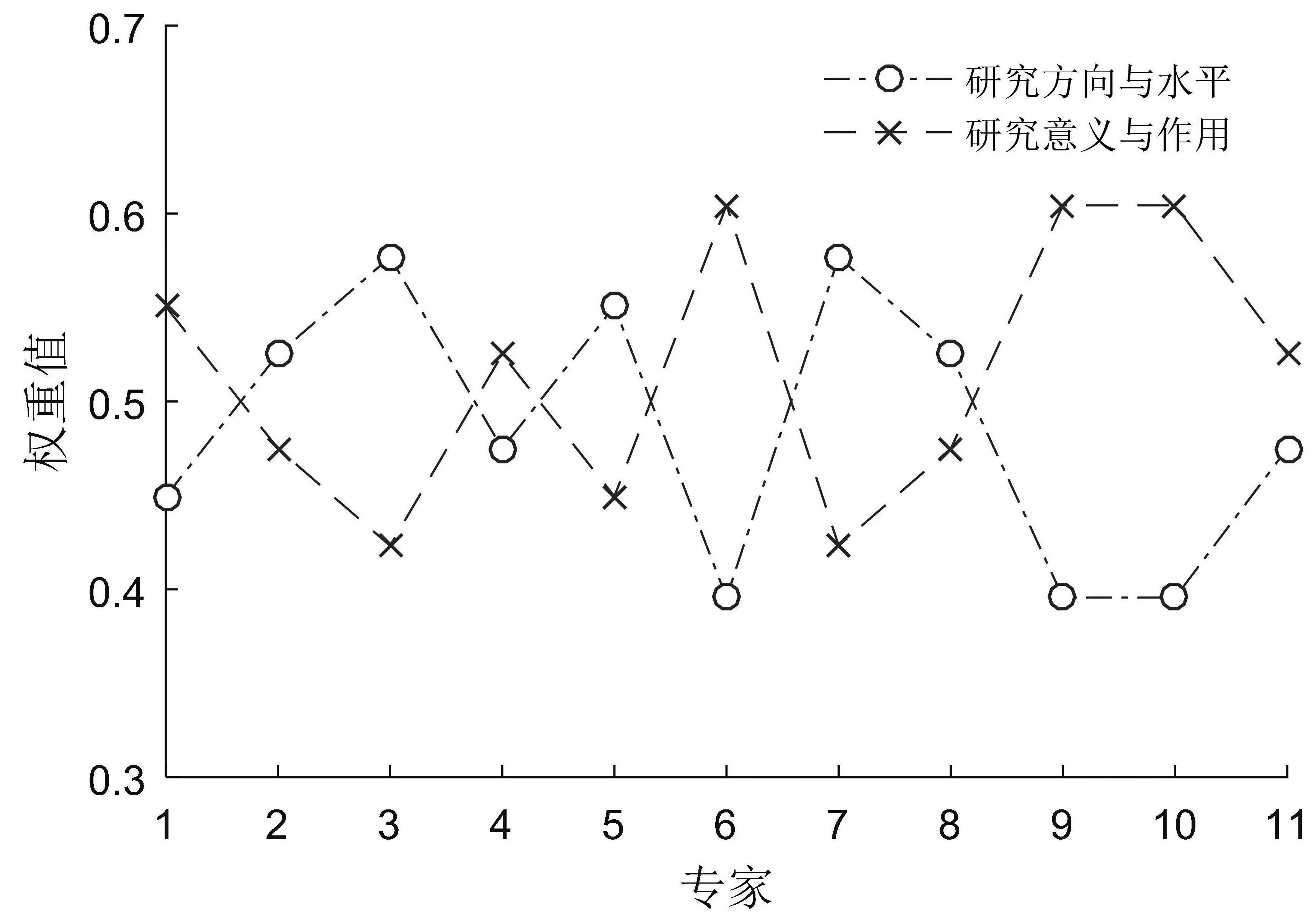
(a)第1个一级指标下二级指标的权重

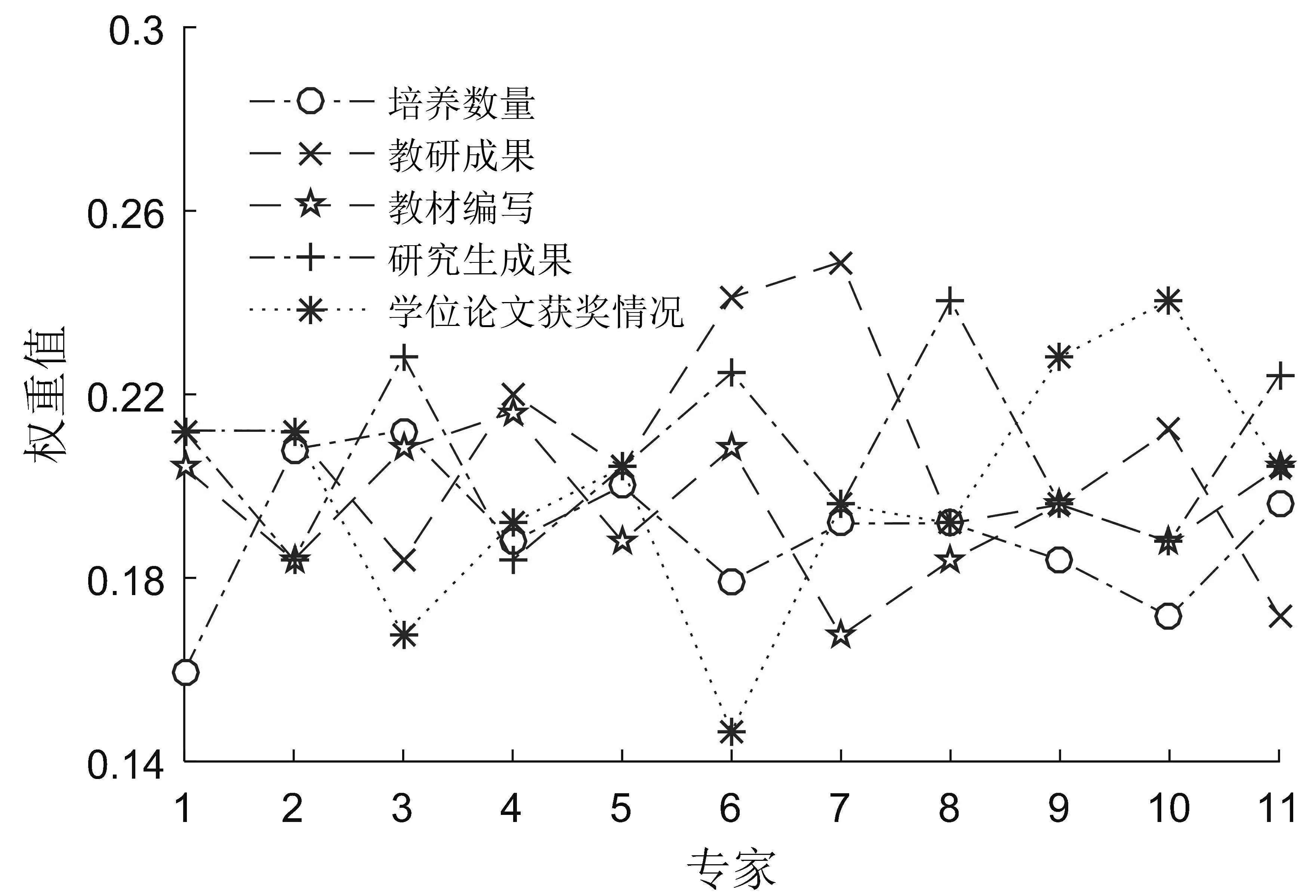
(c)第3个一级指标下二级指标的权重

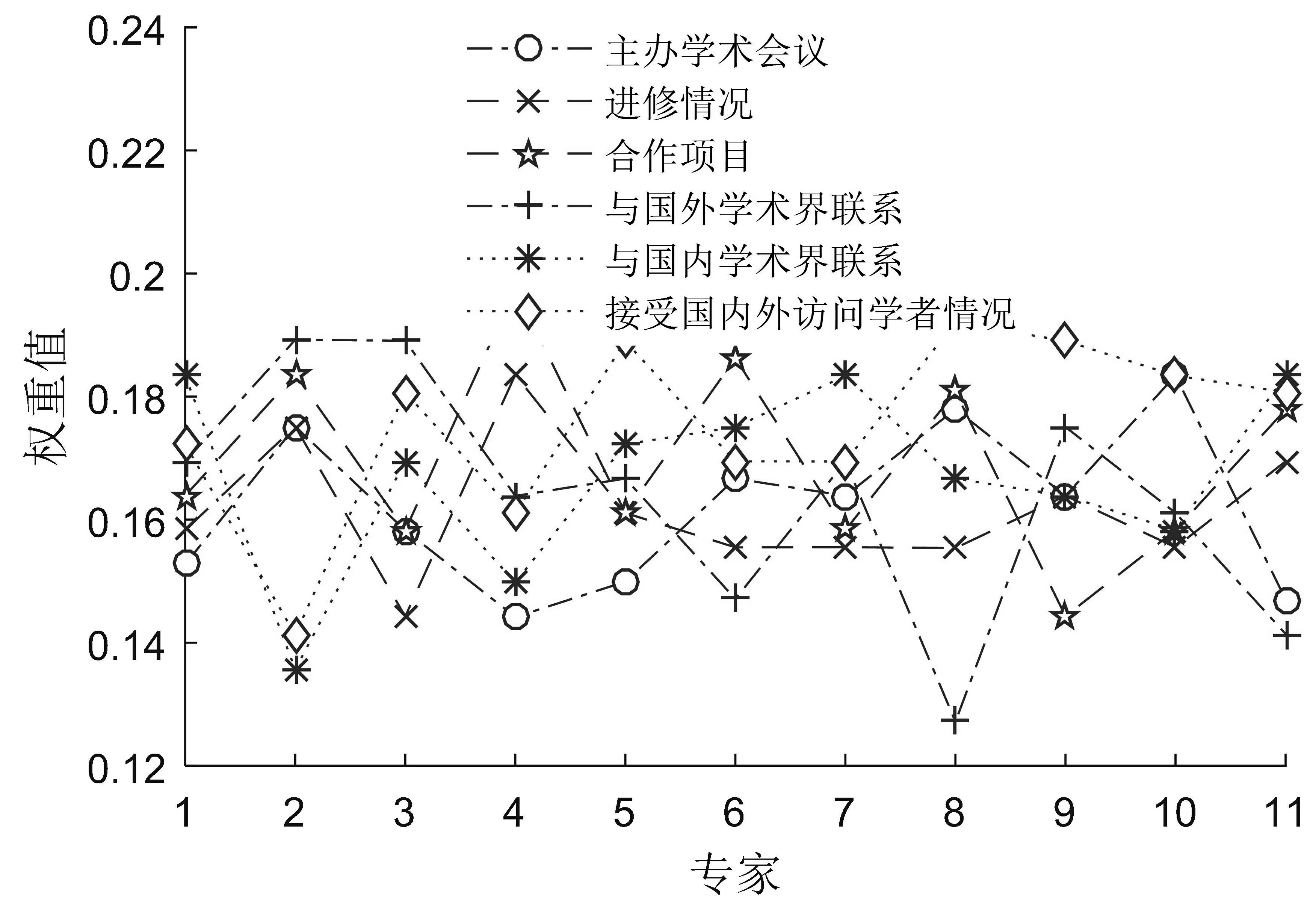
(e)第5个一级指标下二级指标的权重

同理，可以计算出所有一级指标的三角模糊数.专家2对6个一级学科给出的一级指标评价矩阵为

(6)利用确定二级指标权重的方法，得到一级指标的权重矩阵为

W2=[0.1751 0.1301 0.1807 0.1554

0.1864 0.1723]T

同理，可以得到11位专家给出的一级指标权重值如图3所示.

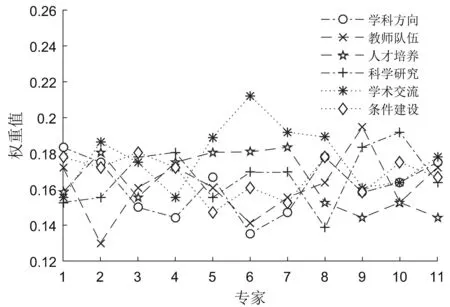
图3 一级指标的权重值

(7)将所有专家给出的一级指标的权重矩阵和评价矩阵进行模糊运算，然后求均值得到综合评价三角模糊数为

(8)对综合评价三角模糊数进行去模糊值，可得

T=[0.5054 0.4986 0.5191 0.4969

0.4872 0.4706]T

由以上结果及最大隶属度原则可知，该校6个一级学科的评价等级均为中，说明各学科的学科优势不明显，区分度较小，办学特色需要进一步提炼.该校6个一级学科排序为：机械工程、设计学、控制科学与工程、轻工技术与工程、管理科学与工程、纺织科学与工程.优势学科应选取机械工程、设计学、控制科学与工程.

4 结语

优势学科评价是地方院校学科建设中的一项重要工作.本文建立了地方院校优势学科评价指标体系，该指标体系共分2级，一级指标6个、二级指标30个，并且结合层次分析法与三角模糊数理论的优点，设计了三角模糊层次分析法的计算算法，该算法通用性好.采用三角模糊层次分析法对地方院校优势学科进行评价，评价过程更加合理，且易于实现计算机编程.通过实例计算，评价结果与实际情况相符，论证了三角模糊层次分析法在地方院校优势学科评价中的可行性.