空间变化离焦模糊红外图像快速复原算法
汪陈跃,雷旭峰,李泽民,杨绍明,何 燕
(昆明物理研究所,云南 昆明 650223)
0 引言
空间变化离焦模糊是红外系统普遍存在的一个问题,产生这一问题的根本原因是受红外光学原理限制,视场中物距差别大的物体无法同时清晰成像。空间离焦模糊红外图像复原算法的目的就是通过图像处理来减弱离焦导致的图像模糊,提升图像质量。
理论研究认为模糊图像是由清晰图像与一个点扩散函数(point spread function,PSF)卷积并叠加上噪声的结果。对于实际模糊图像复原问题,模糊图像已知,但模糊图像的点扩散函数是未知的,且点扩散函数在空间分布上是不一致的,这种模糊称为空间变化离焦模糊。为了复原模糊图像,需估计图像的点扩散函数,为了简化估计点扩散函数问题,可采用理论模型来近似实际点扩散函数,离焦模糊的点扩散函数的数学模型一般可以采用圆盘模型或高斯模型[1],使用近似模型能够将点扩散函数估计简化为估计一个参数(圆盘半径或高斯方差),高斯模型更接近实际图像中的点扩散函数,所以本文研究中选用高斯模型。
空间变化离焦模糊的点扩散函数在空间域上不一致,无法直接使用某一个点扩散函数来复原图像,因而目前空间变化离焦模糊图像复原算法主要有两种方法,第一种是将图像按模糊程度进行分割,对分割后每个区域的点扩散函数进行精确估计,然后使用估计的点扩散函数对对应区域的图像进行复原处理,最后将复原后的区域图像组合为完整的复原图像[2-4];第二种是对图像的每一个像素的点扩散函数进行估计,并根据估计的点扩散函数对每个像素进行复原并组合为最终的复原图像[5]。
由于点扩散函数估计要达到较高的精度需要的计算量大,难以实现快速算法。为了实现空间变化离焦模糊快速算法且满足实时性要求,本文提出使用固定的点扩散函数组对图像进行复原,然后对复原后的图像组进行像素级图像质量评价,利用评价参数将多幅复原图像中的最佳像素组合为最终复原图像。模糊图像复原算法选用截断约束最小二乘法(truncated constrained least-squares,TCLS)复原算法,复原图像的图像质量评价采用基于复原图像空间二阶导(拉普拉斯算子)的特点提出新的评价方法。
1 离焦模糊图像快速复原算法
1.1 离焦模糊图像理论模型
模糊图像的数学模型可用g=f⊗k+n表示。式中:g是模糊图像;f是清晰图像;k是点扩散函数;n是噪声;⊗是卷积符号。离焦模糊点扩散函数的数学模型一般采用圆盘分布或高斯分布[1]。
圆盘分布来源于几何光学中的模型,根据高斯成像公式和几何相似性,可以推导出点光源成像为一个圆盘,其圆盘直径由焦距、物距等共同决定[1]。
圆盘离焦模型的点扩散函数可以表示为[1]:

式中:R是模糊半径。
高斯模型来源于算法的实际实践,暂未有明确的光学理论原理解释,它的点扩散函数数学表达如下[1]:

式中:σ是模糊参数,即高斯模糊标准差。
高斯模型更接近实际图像中的点扩散函数,所以研究中使用高斯模型。
1.2 TCLS复原算法
本文提出的算法需使用多个不同的点扩散函数分别复原红外图像,因此需选择能够快速实现的复原算法以减少计算量,由于一般的复原算法都需转换到变换域进行复原(如维纳滤波复原算法)或需要通过多次迭代(如Lucy-Richardson 图像复原算法)来实现,不利于算法的硬件实现,本文选择TCLS算法作为复原算法,TCLS算法的复原过程为空间域卷积计算,便于硬件实现快速处理。
TCLS算法由Kim 提出,TCLS算法将约束最小二乘法(constrained least-squares,CLS)在变换域的操作转化到空间域,该算法执行速度快[6]。
CLS的复原公式为[6]:

式中:H(u,v)是点扩散函数h(x,y)的傅里叶变换;R(u,v)是空间域复原滤波器r(x,y)的傅里叶变换;P(u,v)是的傅里叶变换;λ是与图像噪声相关的系数,简称噪声系数,取值范围(0,1),图像噪声越小,噪声系数取值越小。
CLS复原滤波器是频域操作,使用傅里叶逆变换可以将它转换到空间域,如下式[6]:

式中:F-1是傅里叶逆变换;r(x,y)是空间域复原滤波器。由于一个超大尺寸的滤波器计算是不现实的,我们需要对它进行截断,Kim 提出使用升余弦函数进行截断,相比高斯函数,它能更好地保留高频细节。最终的复原操作可以表达为[6]:

式中:rT(x,y)是截断后的CLS复原滤波器;g(x,y)是输入的模糊图像;fT(x,y)是初步复原的图像。
TCLS 将复原操作转化为卷积计算,减少了傅里叶变换过程,在实时成像系统中可以实现快速处理。
针对TCLS算法复原图像存在的振铃和噪声问题,Kim 采用了空间自适应噪声平滑(spatially adaptive noise smoothing,SANS)算法进行处理,它利用输入模糊图像的局部方差将输入模糊图像和复原后的图像进行融合,融合方程和依据局部方差计算的比例参数见下式[6]:

TCLS算法的优点是复原过程为空间域的卷积计算,不需要对输入图像进行傅里叶变换或小波变换,硬件上可以采用有限脉冲响应滤波器实现,所以TCLS复原算法的硬件实现难度较小。TCLS算法的缺点是随着需要复原的模糊的标准差增大,空间域复原滤波器的尺寸也增大,滤波器尺寸过大会导致计算量少的优势消失,所以TCLS算法适合于模糊程度较小时,有一定的局限性。
图1是TCLS 处理的效果,其中(a)是调焦清晰图,(b)是同场景调焦模糊图,(c)是(b)经过TCLS复原后的图像(复原滤波器对应标准差为1.8,噪声系数0.0001),复原图像细节得到增强,但噪声和振铃明显,(d)是(c)经SANS 处理后的图像,SANS 实现了降噪和去振铃,去振铃后的图像能够使用简单的图像质量评价方法进行评价。

图1 TCLS算法复原效果对比Fig.1 Comparison of image of blurred and restored by TCLS
2 空间变化离焦模糊图像复原算法
2.1 提出的空间变化离焦模糊图像复原方法
Cheong 利用模糊图像的局部梯度对每个像素的点扩散函数进行估计,然后根据估计的点扩散函数参数从预设的多个TCLS 滤波器中选择并计算最终使用的TCLS 滤波器,实现了不需迭代的快速复原[5]。Cheong的算法的局限性是该算法的点扩散函数估计推导是基于孤立边的,当图像复杂时,点扩散函数的估计精度下降明显[5]。为了去掉点扩散函数估计的流程,本文提出针对不同参数TCLS复原的图像进行区域图像质量评价的方法,将不同参数复原图像中的最佳像素组合为最终的输出图像。
本文提出的方法的流程图见图2。首先使用m个不同标准差σi的点扩散函数对应的TCLS复原算法复原模糊图像并使用SANS算法去振铃,其中标准差σi(i=1~m)为递增序列,而输入图像可以认为是标准差为0的TCLS+SANS复原算法复原的图像,将这m+1个图像按标准差递增的关系编号,编号分别为1到m+1,然后对每幅复原图像按像素进行区域图像质量评价获得m+1幅图像质量图,将每个像素位置的图像质量评价指标最大的图像编号输出,生成最佳像素的复原图像编号图,由于图像质量评价仅使用了区域信息,会存在错误,使用中值滤波处理图像编号图,去除错误值,最后使用处理后的图像编号图将复原图像组合为复原图像。本文提出的方法无需对点扩散函数进行估计,而且利用了TCLS算法可以并行实现的特点,可以实现空间变化离焦模糊图像的快速复原。
2.2 空间变化离焦模糊复原算法实现
模糊图像与清晰图像的区别主要集中在边附近,模糊图像中边的宽度大,边不够清晰,而复原图像中边较为清晰。为了分析图像边的情况,使用拉普拉斯算子与图像卷积获得拉普拉斯处理的图像,拉普拉斯算子强调的是图像中灰度的突变,而灰度突变一般对应于图像中清晰边。拉普拉斯滤波图像中的“零交叉”位置是图像的边,一个像素为“零交叉”像素时,在其四邻域内同时存在正负像素。随着复原滤波器的标准差不断增大,复原图像中的边逐渐变清晰,边的边缘出现明显的“零交叉”,如果继续增大,图像中出现超出表达范围的结果(压减到能表达的最大值),图像反而质量下降。式(8)为拉普拉斯算子与图像卷积计算:

式中:fi(x,y)是按照复原滤波器的标准差由小到大对复原后图像按1~m+1 进行编号得到复原图像组;Li(x,y)为对应的拉普拉斯滤波后的图像。
检测图像中的“零交叉”可以使用统计的方法,计算一个像素的四邻域的像素灰度值的绝对值之和与四邻域的像素灰度值和的绝对值的差值,当该像素为“零交叉”时,差值大于0。

Ldi(x,y)为计算的表征边强度的指标,会受图像区域像素分布影响,为了能够比较不同标准差的复原滤波器的复原结果,用Ldi(x,y)除以Li(x,y)的绝对值来去除像素周边分布的影响,计算过程为式(10),其中ε是为了避免除零运算而设的大于零的值,ε的取值较小即可。


图2 提出的算法流程Fig.2 The proposed algorithm flow
Ldi(x,y)最大的像素认为是图像质量最好的像素,使用对应的图像编号i作为该像素位置的最优像素所在的图像编号,生成最优像素图像编号图Id(x,y)。
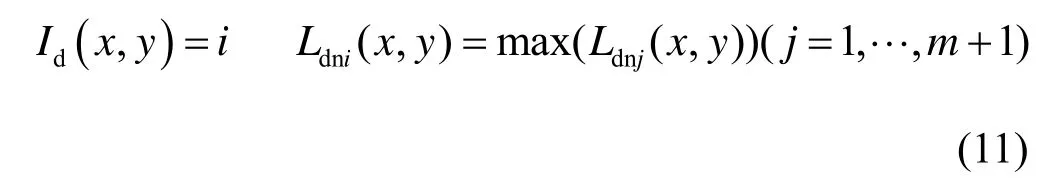
由于Id(x,y)的计算仅使用了像素周边区域的图像信息,当周边区域为平滑区域,没有边的信息时,计算结果会出现错误,而相邻像素的离焦程度具有相关性,在很小的区域内,最优像素图像编号不应出现剧烈变化,所以对编号图Id(x,y)按一定大小的区域(如7×7)取中值作为区域中心像素的编号。对于有边的区域,计算结果正确的像素占多数,取中值处理能剔除错误值;对于大的平滑区域,由于不同参数的复原图像基本无变化,取中值并不会导致复原图像出现错误像素。
对Id(x,y)的每个像素按区域取中值获得最终的最优像素图像编号图Idf(x,y),将Idf(x,y)中每个像素Idf(i,j)对应的复原图像中(i,j)位置的像素值作为最终复原图像(i,j)位置的像素值,生成最终复原图像。

图3是使用提出的复原方法复原的图像和过程图像,使用提出的图像质量评价方法能获得较好的效果。
3 空间变化离焦模糊图像复原算法性能分析对比
3.1 空间变化离焦模糊图像复原算法对比
为了测试本文提出的算法,使用本文算法、Zhang的算法[4]和Cheong的算法[5]分别对两幅空间变化离焦模糊图像进行复原。Zhang的算法是根据输入图像估计出点扩散函数分布图,然后根据估计的点扩散函数分割图像,对每个区域分别使用估计的点扩散函数进行复原,然后组合为复原图像,复原图像经降噪和去振铃处理后输出。Cheong的算法则是根据图像的梯度估计点扩散函数,然后依据每个像素估计的点扩散函数使用TCLS算法复原像素,然后组合输出最终图像。
图4是对图像1 使用不同算法复原的图像,图5是对图像2 使用不同算法复原的图像,本文提出的算法复原的图像最好,图像的细节丰富且对比度大,Cheong的算法复原的图像细节丢失多,而Zhang的算法复原的图像效果不显著。Cheong和Zhang的算法的复原效果差是因为点扩散函数估计出现了较大误差,高精度的点扩散函数估计是很难实现的。

图3 复原图像和部分过程图像Fig.3 Restored image and partial process images
表1为使用信息熵和标准差进行量化分析复原图像的结果,Zhang的算法的指标与输入图像最接近,与Zhang的算法复原的图像无显著变化一致,Cheong的算法的指标提升大,但实际图像细节丢失严重,本文提出的算法两个指标均有提升。

图4 图像1 复原图像对比Fig.4 Comparison of the restored image of image 1

图5 图像2 复原图像对比Fig.5 Comparison of restored images of image 2
为了比较算法运行速度,在同一仿真平台和软件上进行算法仿真并统计算法运行时间。仿真平台,CPU:I5-8400,内存:16 GB,仿真软件为Matlab 2017b。3个算法对测试图像的复原运行的时间见表2,其中Zhang的算法的复原运行时间最长,而本文提出的算法运行时间最短。

表1 复原图像质量评价对比Table1 Comparison of image quality assessment of restoration algorithms

表2 复原算法运行时间对比Table2 Comparison of running time of restoration algorithms s
3.2 本文提出的算法的硬件实现分析
对于M×N的输入图像,若算法预设的复原滤波器对应的离焦模糊标准差的最大值为σ(σ≤3),则最大的复原滤波器尺寸为n×n(n=6×σ+1),可计算得本文提出的算法的时间复杂度为O(M×N×n2)。
本文提出的算法复原过程为多个预设的复原滤波器分别进行卷积计算,卷积计算在硬件上可以使用有限脉冲响应滤波器实现,且多个预设的复原滤波器可以进行并行计算;复原滤波器的尺寸限定在n×n,卷积计算硬件优化后能够在3n行之内完成,后续的SANS和图像质量评价都使用的是简单算法,不会产生大的延迟,所以本文提出的算法能够满足实时性要求,但由于存在n×n的卷积计算,算法的计算量大,对硬件资源要求高,后续研究中可进一步优化复原的卷积过程来降低计算量。硬件实现时还需考虑算法对存储和传输带宽的要求;本文提出的算法中使用的复原滤波器是预设好的,在硬件实现中可以直接写入程序,无需进行大量读写操作,对传输带宽要求低;本文提出的算法无需存储整幅图像,对存储要求低。综上所述,本文提出的算法能够进行硬件实现,并能达到实时性要求,但计算量大,对硬件资源要求高。
4 结论
空间变化离焦模糊图像复原是提升红外图像的一个重要途径,本文提出的基于图像质量评价的方法能够快速较好地复原模糊图像,算法达到很好的复原效果,与基于估计点扩散函数的方法对比,该算法能大大降低计算量,同时不需要迭代的过程,便于硬件实现。本文复原后图像仍然存在一定的振铃,部分原因是采用的高斯模型与实际点扩散函数有误差,后续研究可针对实际的光学系统离焦模糊进行标定,获得更精准的模糊模型,进而提升复原图像的效果。

