鼠笼弹性支承结构优化设计方法

李明明， 王东强， 陈坤旭， 董学武， 于贺春， 姜海芹

(中原工学院机电学院， 郑州 451191)

鼠笼弹性支承在各类航空发动机中使用较广泛，其用途为调节航空发动机转子系统的临界转速从而实现减振[1]。鼠笼刚度对发动机的性能影响较大，若其刚度达不到设计要求则可能引起发动机产生过大的振动，从而对发动机造成严重的破坏[2]。鼠笼弹性支承在工作过程中也常会因为过大的集中应力而出现疲劳裂纹甚至鼠条断裂，从而引发重大事故[3-4]。为了提高发动机转子系统的稳定性以及其动力学特性研究的可靠性，对鼠笼结构进行优化从而得到鼠笼刚度准确值以及最大程度降低鼠笼的最大应力是非常有必要的。

目前，中外较多学者对带有弹性阻尼支承结构的转子系统进行了大量的理论和实验研究[5-13]。对于鼠笼弹性支承刚度的研究，多是刚度值的理论计算以及试验测试。如徐方程等[14]通过试验和有限元软件对6个不同结构鼠笼弹性支承的静刚度分别进行了测试和计算，分析了其静刚度的影响因素。张萍等[15]提出了一种通过求解鼠笼式弹性支承的第一阶固有频率，从而计算鼠笼式弹性支承刚度的新方法；付才高等[16]发现了转子系统运转时鼠笼弹性支承受到了重力和不平衡力作用，并推导了传统的鼠笼弹性支承刚度的计算公式；徐宁[17]采用参数公式和有限元两种方法对鼠笼刚度进行了理论分析，并通过试验得到了刚度随鼠笼结构参数的变化规律，对鼠笼式弹性支承的刚度计算公式进行了修正；彭京徽等[18]通过实验测试了鼠笼弹性支承的刚度，基于有限元法计算了鼠笼弹性支承的刚度，分析了其影响因素，并考虑了鼠条截面为梯形而非矩形，重新推导了鼠笼弹性支承刚度的计算公式。关于鼠笼弹性支承结构优化的研究较少。文献[3]建立了鼠笼弹性支承刚度优化的数学模型，基于MATLAB的遗传算法软件包进行了优化，此方法可大幅度缩短设计时间，但其精确度完全取决于计算公式的精确性，由于计算公式未考虑鼠条根部圆角等因素，故计算精度较低；文献[19]基于参数化建模思想, 提出了分步优化设计方法，运用了有限元优化技术，避开了计算公式带来的误差，但鼠笼刚度的设计精度仍需进一步提高，设计过程中需多次迭代，设计时间也仍需进一步缩短。

鉴于此，现提出一种具有高精度和高效率的鼠笼结构优化设计方法。首先，建立带有非线性约束的鼠笼结构优化数学模型，基于该模型运用有效集算法对鼠笼结构进行优化；然后，根据优化结果建立鼠笼参数化有限元模型，通过关联性分析，挑选出对鼠笼刚度较敏感的结构参数，考虑到遗传算法不易陷入局部最优的特点，采用遗传算法对结构做进一步优化。

1 鼠笼弹性支承优化数学模型的建立

鼠笼弹性支承用于航空发动机转子系统中，其安装时一端固定于机匣轴承座上，一端悬臂，其内部放置用于支承转子的轴承，悬臂端机匣内常安装钢环，通过钢环与悬臂端的间隙可达到降振效果[16]。鼠笼式弹性支承的结构简图如图1所示，套筒上呈偶数分布若干鼠条，通过调节鼠条的长度、宽度、厚度以及数量可以实现鼠笼弹性支承刚度的调整，由于加工过程需保证两个加工平面平行，故鼠条的截面为梯形。

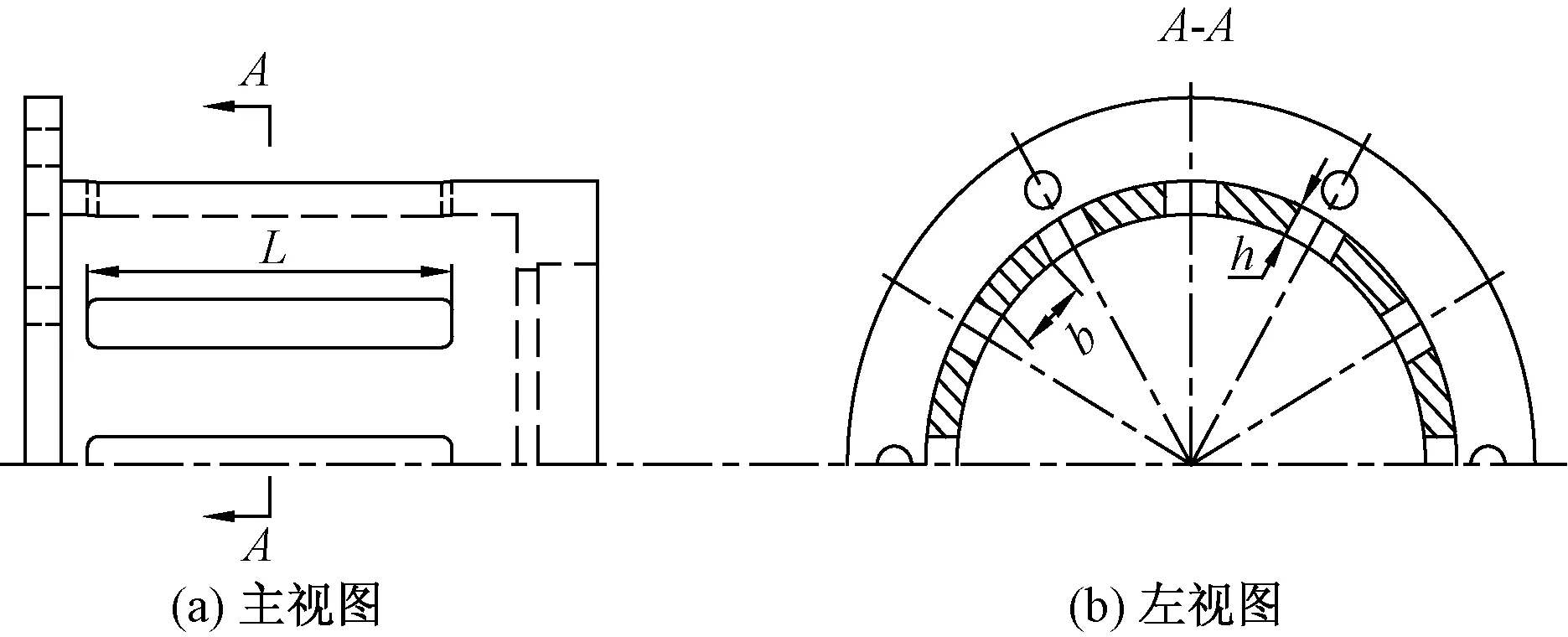
b为笼条宽度；h为笼条厚度；L为笼条长度

文献[3]给出了考虑各笼条截面主弯曲方向与笼条受力方向不平行特点的柔度、疲劳应力参数化计算公式，虽然该公式未考虑鼠笼的梯形截面等因素，但考虑到公式的简便性，较易建立鼠笼优化数学模型，故采用该公式进行初始优化，另外考虑到加工装配的便利性，所有的鼠条宽度之和应不大于其周长的一半[19]，公式为

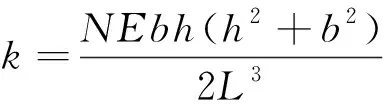
(1)

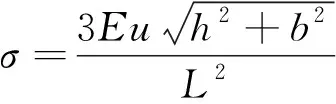
(2)

(3)

式中：k为鼠笼刚度；σ为鼠笼应力；N为笼条数量；E为鼠笼弹性模量；u为加载时鼠笼变形量；D为轴承外径。鼠笼优化问题为鼠笼弹性支承在满足刚度要求以及加工要求的条件下，其疲劳应力值最小。因此，鼠笼的优化目标为疲劳应力最小，约束条件为刚度要求以及加工要求，建立带非线性约束的鼠笼弹性支承优化数学模型为

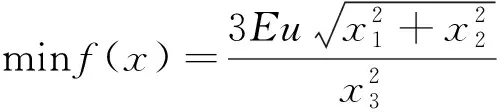
(4)

x2x4≤πD/2

(5)

s.t.Li≤xi≤Hi,i=1,2,3,4

(6)

(7)

式中：x1为笼条厚度；x2为笼条宽度；x3为笼条长度；x4为笼条数目；δ为支承刚度的倒数；Li、Hi分别为设计变量xi的下限和上限。

2 鼠笼弹性支承优化策略

虽然利用有限元优化方法进行鼠笼优化能提升设计精度，但直接利用该方法优化较费时，为了缩短设计周期，首先基于建立的数学模型进行初始优化，考虑到数学模型中的非线性约束，选择优化效率较高的有效集算法为优化算法，然后再利用workbench优化模块中的遗传算法完成鼠笼的进一步优化。鼠笼弹性支承结构优化流程如图2所示，具体优化步骤可概括如下。

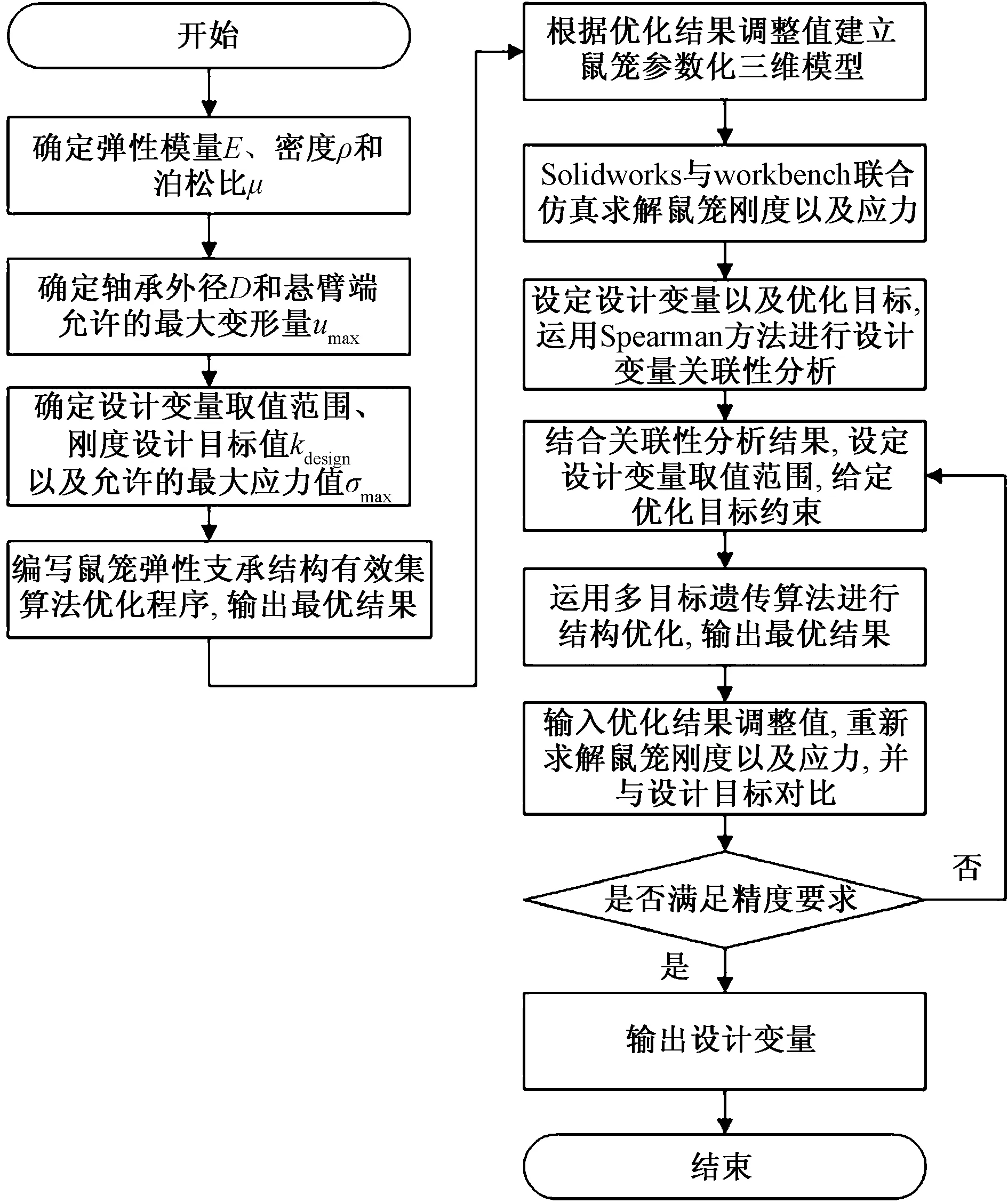
图2 鼠笼弹性支承结构优化流程图Fig.2 Optimization flow chart of squirrel cage elastic support structure

(1)根据鼠笼的材料，确定弹性模量E、密度ρ和泊松比μ；再根据鼠笼具体结构以及安装工况，确定轴承外径D和悬臂端允许的最大变形量umax；最后根据工程需要，确定各设计变量的取值范围、刚度设计目标值kdesign。

(2)将确定的参数值代入数学模型，运用基于MATLAB的有效集算法工具箱，编写鼠笼弹性支承结构参数优化程序，确定满足约束的最优值。

(3)考虑到加工的便捷性，调整优化结果数值，根据调整值运用SolidWorks建立鼠笼三维模型，将鼠条的长度、宽度、厚度和数量进行参数化。

(4)采用SolidWorks与workbench的联合仿真方法求解鼠笼弹性支承刚度以及疲劳应力，设定设计变量以及优化目标，运用spearman方法进行设计变量之间的关联性分析，挑选出比较敏感的设计变量。

(5)结合关联性分析结果，设定设计变量取值范围，给定优化目标约束，运用遗传算法进行鼠笼弹性支承结构的进一步优化，输出最优结果。

(6)为便于加工，对最优结果进行调整，将调整值作为新设计变量进行输入，求解出鼠笼刚度以及疲劳应力，并与设计目标进行对比，若满足精度要求，则输出设计变量终止优化，若不满足，则基于此优化结果，重新设定设计变量取值范围，继续优化直到得出满意结果。

3 算例

为了与已有的鼠笼结构优化方法对比，选取与文献[3]和文献[19]相同的鼠笼弹性支承材料、设计变量取值范围、设计值。鼠笼弹性支承的材料为40Cr，其弹性模量为210 000 N/mm2，泊松比为μ=0.3，密度为7 900 kg/m3。设计变量取值范围为鼠条长度L∈[20,45] mm，鼠条数量N∈[24,60]，鼠条厚度h∈[3,6] mm，鼠条宽度b∈[3,6] mm。鼠笼刚度设计值kdesign=16 670N/mm以及允许的最大应力值σmax≤[σ]=200 MPa。根据鼠笼具体结构以及安装工况，确定轴承外径D为100 mm，悬臂端允许的最大变形量umax=0.12 mm。

将上述参数代入数学模型中，运用MATLAB工具箱中的非线性优化函数fmincon，选择有效集算法，根据数学模型编写优化程序，计算得到鼠笼弹性支承结构最终优化结果为h=3.857 1 mm，b=3 mm，L=45 mm，N=52.359 9，考虑到加工的便捷性，选取结构参数h=4 mm，b=3 mm，L=45 mm，N=52，得到的刚度和应力分别为k=17 975 N/mm，σ=186.666 7 MPa，优化函数迭代情况如图3所示，函数仅经过三次迭代就达到了比较稳定的数值，优化效率较高。

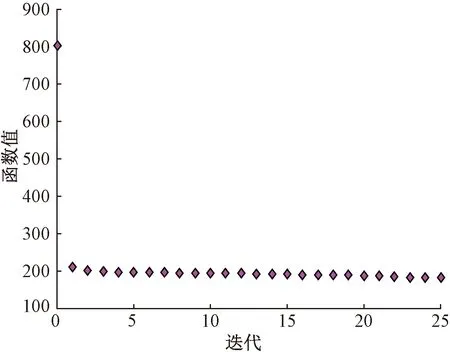
图3 各代优化函数值Fig.3 Optimization function values of generations

基于优化参数建立鼠笼弹性支承的有限元模型，对鼠条的长度、宽度、厚度和数量进行参数化，将参数化有限元模型导入workbench中进行结构静力学分析。综合考虑计算的效率和精度，模型网格划分如图4所示，为了使得鼠笼达到设计刚度的同时变形量也达到最大，总加载力的大小设置为F=ukdesign=2 000.4 N。考虑到鼠笼承受载荷时，可以近似认为轴承外圈下表面与鼠笼内表面的接触面均匀受力，因此在与轴承接触的鼠笼下表面上每个节点施加大小和方向相同的力[20]。根据鼠笼的安装条件，完全约束鼠笼安装端螺钉孔的自由度，有限元模型的约束和加载方式如图5所示。计算得到鼠笼加载变形量以及应力如图6和图7所示。

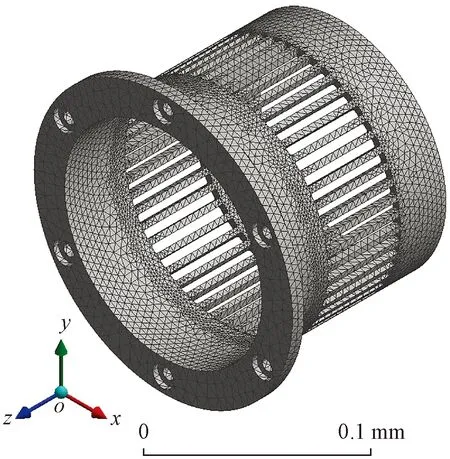
图4 鼠笼有限元网格划分Fig.4 Squirrel cage finite element mesh division

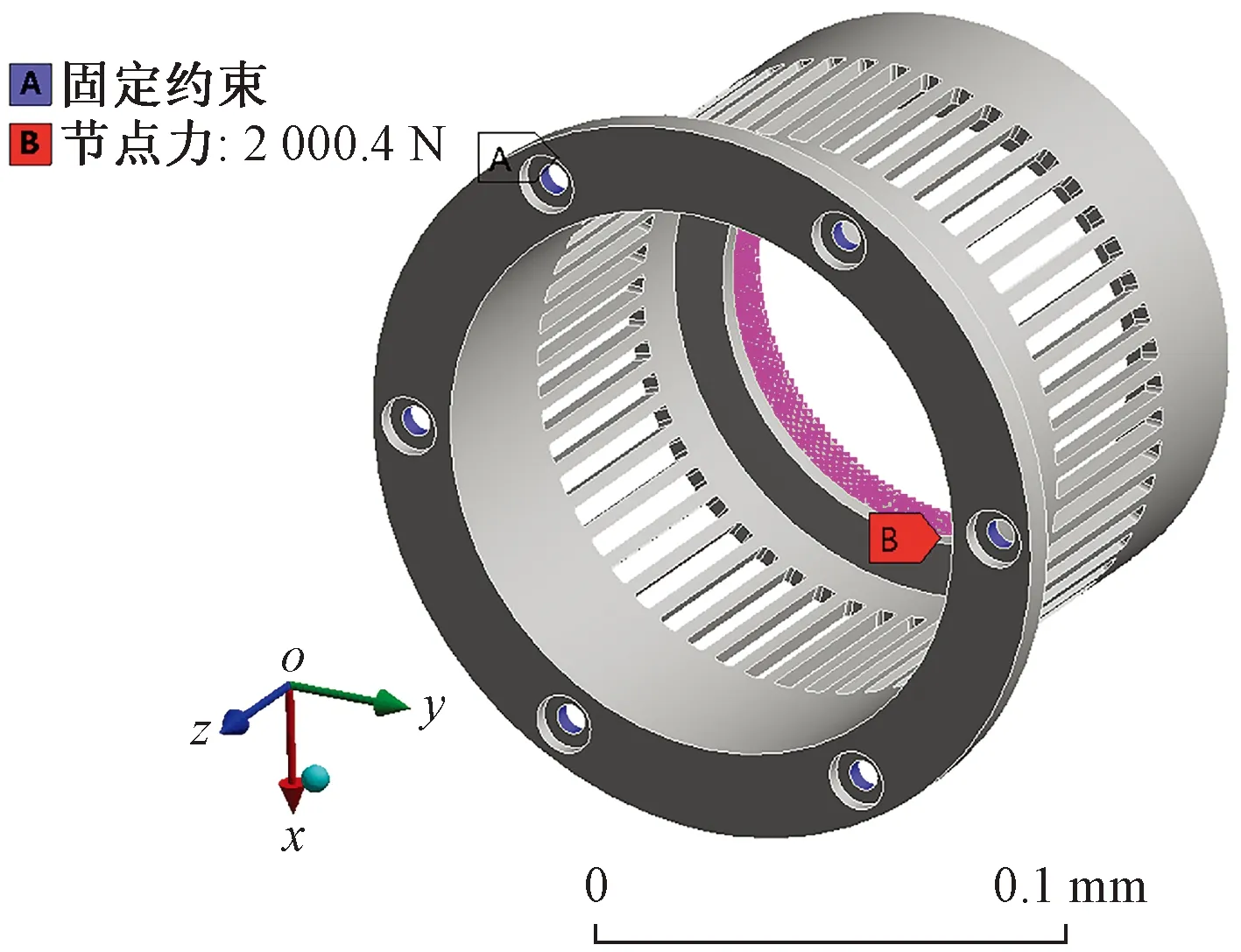
图5 有限元模型约束和加载方式Fig.5 Constraint and loading mode of finite element model

图6 鼠笼加载变形图Fig.6 Squirrel cage loading deformation diagram

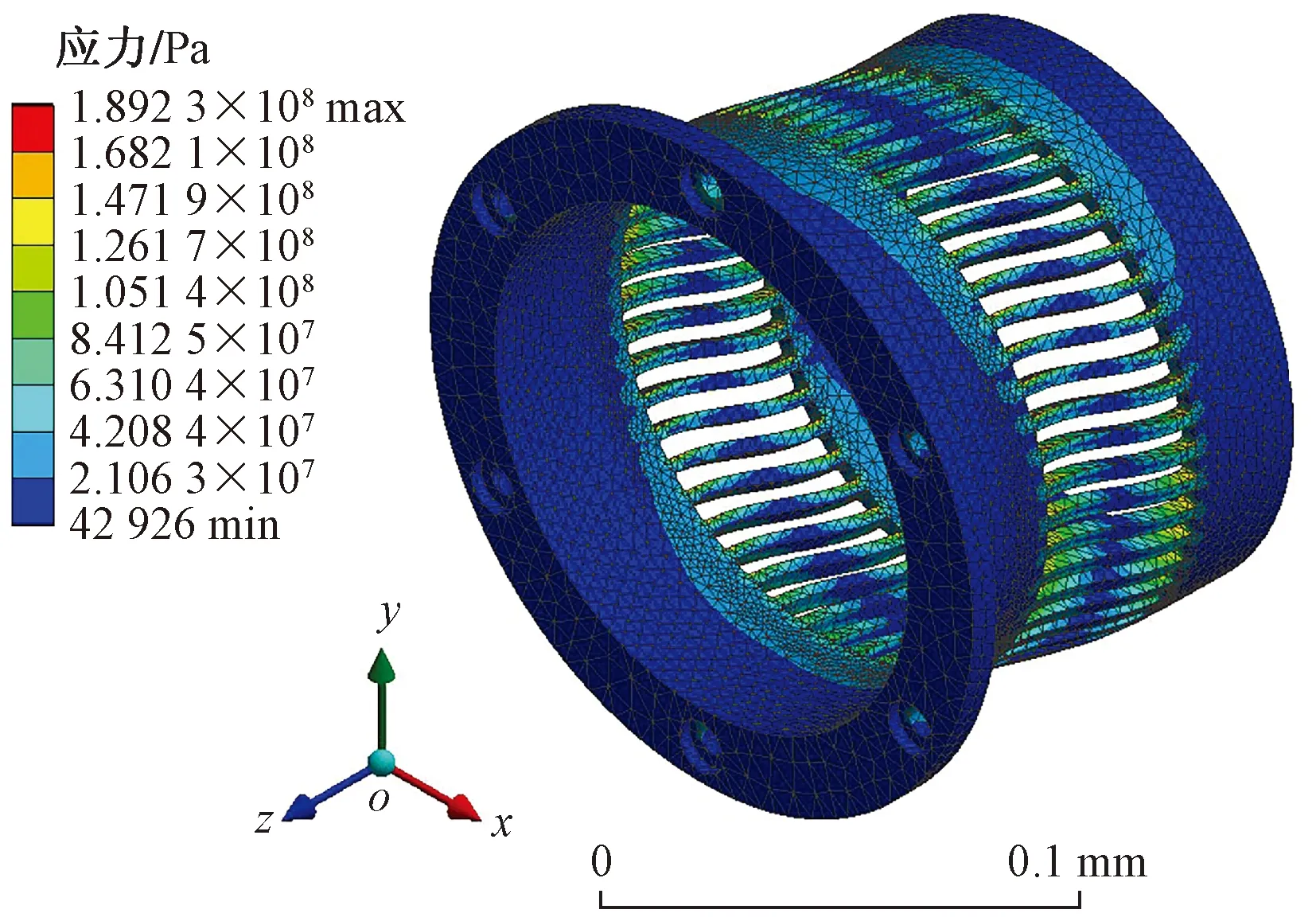
图7 鼠笼加载应力云图Fig.7 Stress nephogram of squirrel cage loading

根据有限元计算结果，得到鼠笼的刚度k=F/u=11 231 N/mm，应力值为189.23 MPa，其刚度值与设计值相差较大，因此需要运用有限元优化方法完成进一步优化。由于有限元方法不能直接计算出鼠笼刚度值，因此将优化过程中的刚度约束条件转化为对鼠笼最大变形量的限制[19]。为了提高优化效率，首先采用Spearman法进行设计参数关联性分析，从而确定对鼠笼弹性支承最大变形量敏感性较高的设计参数，分析得到参数关联性云图如图8所示。

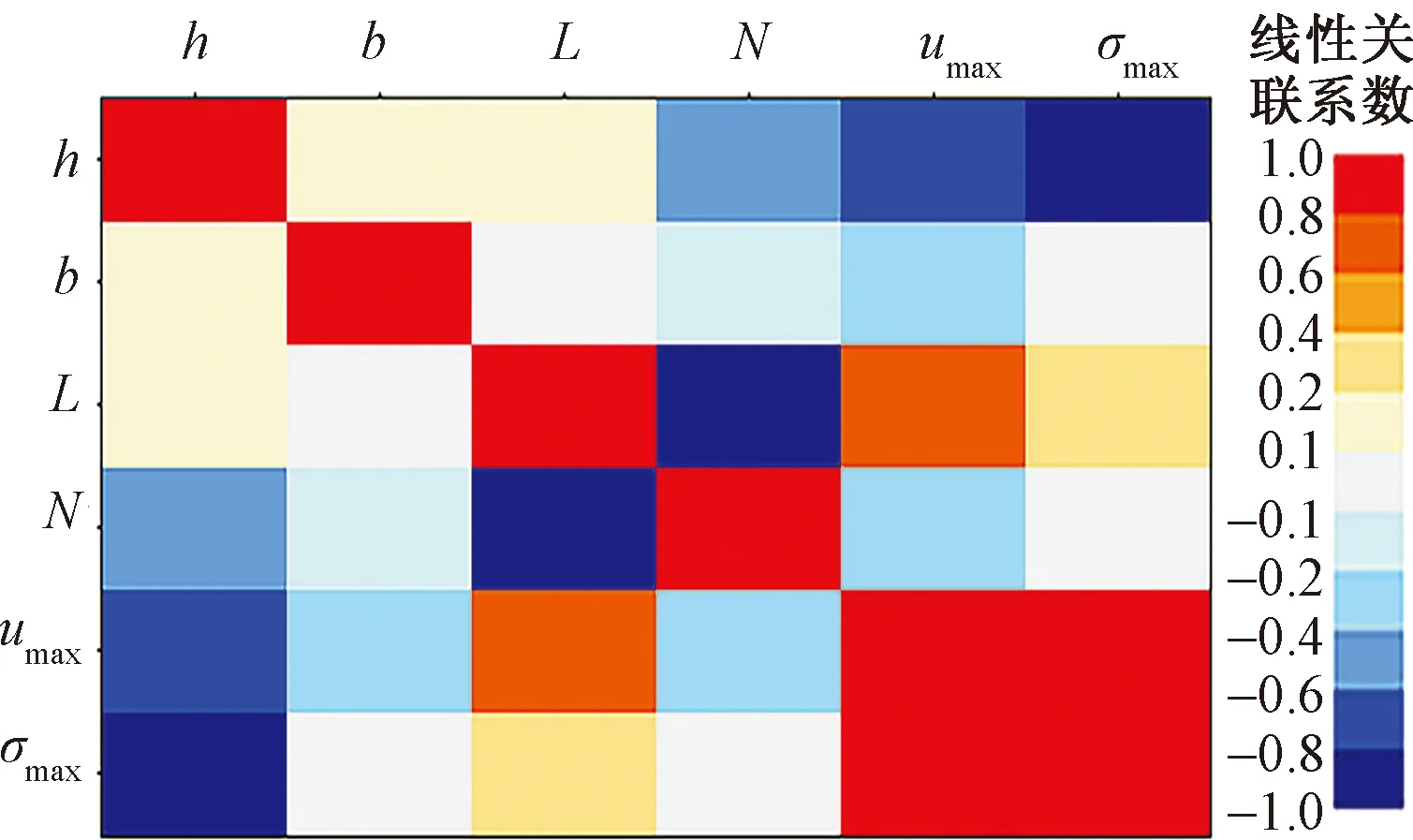
图8 参数关联性云图Fig.8 Parameter correlation nephogram

根据图8可知，严重影响鼠笼的最大变形量的设计参数为鼠条的厚度h和长度L，厚度对最大变形量的线性关联系数为-0.6，长度对最大变形量的线性关联系数为0.6，均高于其他参数，因此选择鼠条的厚度和长度作为优化变量。根据关联系数的符号可知，为降低鼠笼最大变形量，应增大鼠条厚度和减小鼠条长度，确定设计参数的取值范围为h∈[4,5] mm，L∈[38,43] mm。以鼠笼的最大变形量和最大应力为优化目标，为缩短计算时间，设置样本数为10，运用多目标遗传算法对鼠笼结构参数寻优，得到优化可行点如图9所示，其数值如表1所示。

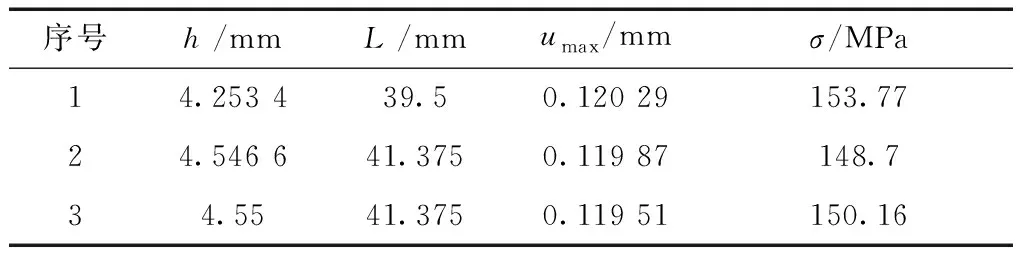
表1 遗传算法优化结果

图9 遗传算法优化可行点Fig.9 Feasible point of genetic algorithm optimization

为方便加工，对优化结果进行调整，将调整值作为输入参数重新进行有限元计算，通过计算结果的对比，最终确定设计变量的值为h=4.5 mm，L=41 mm，计算得到鼠笼的最大变形量和最大应力如图10和图11所示。

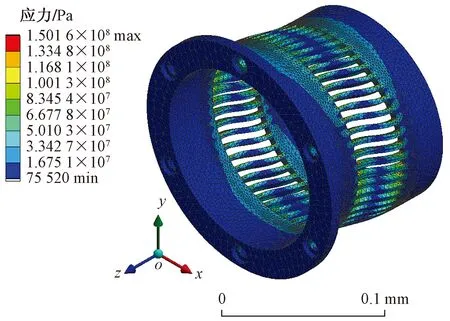
图11 优化后鼠笼应力云图Fig.11 Stress nephogram of squirrel cage after optimization

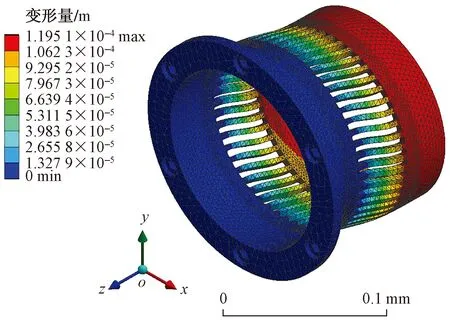
图10 优化后鼠笼变形图Fig.10 Squirrel cage deformation diagram after optimization

本文优化结果与文献[3]中遗传算法和文献[19]中分步优化方法的优化结果的对比如表2所示。由表2可知，运用本文优化方法得到的鼠笼刚度精度较高，最大应力值较小，由于初始优化较大程度缩小了有限元优化设计变量的优化范围，因此其迭代次数较少，故优化效率也较高。

表2 3种优化方法的优化结果对比

4 结论

提出了一种鼠笼弹性支承结构优化方法。首先，运用有效集算法对建立的数学模型进行鼠笼结构参数寻优，然后基于优化结果，采用有限元优化方法对鼠笼结构继续优化，此方法联合了计算公式优化方法和有限元优化方法。通过算例对鼠笼弹性支承结构参数优化的过程中，可以得到以下结论。

(1)基于建立的数学模型，运用有效集算法对鼠笼结构进行优化，可以在满足非线性等式以及不等式的约束的同时以较快的速度获得最优结果，但计算精度较差，运用该方法进行初始优化可较大程度缩小设计参数优化范围。

(2)基于有效集算法的优化结果，建立参数化有限元模型，采用参数关联性分析获得关键性参数，运用遗传算法进行鼠笼结构参数优化。在计算公式优化方法的基础上进行有限元优化，可明显减少优化迭代次数以及提高优化精度。

(3)提出的优化方法将计算公式优化的高效率与有限元优化的高精度进行了结合，具有较大的实用价值，对鼠笼弹性支承的结构设计方案的筛选具有指导意义，对其他结构的优化具有一定的参考意义。