鼠笼弹性支承刚度的数值仿真及影响因素研究

周海仑，曹刚毅，冯祚崐，闫玉奇，尹训彦

（1.沈阳航空航天大学 航空发动机学院，辽宁 沈阳 110136；2.辽宁省航空推进系统先进测试技术重点实验室，辽宁 沈阳 110136）

0 引 言

航空发动机、地面燃气轮机等旋转机械的工作转速与各阶临界转速之间的安全裕度需满足20%的安全裕度要求[1]。为了满足这一安全要求，常常会在转子系统的支承位置加入鼠笼弹性支承，并通过控制鼠笼弹性支承的刚度来使转子系统具有柔性，进而控制、调整临界转速[2]。为了能够准确地控制鼠笼刚度，学者们对鼠笼弹性支承开展了大量的研究。

宴砺堂等[3]初步推导了鼠笼刚度的理论计算公式。但后续学者在研究过程中发现，用该公式计算的刚度精度较低。于是冯国全等[4]根据各笼条截面主弯方向与受力方向不一致的特点研究了鼠笼刚度的优化计算公式。但徐宁[5]在研究过程中发现，随着鼠笼刚度的增加，优化公式的计算精度逐渐降低。为此，彭京徽[6]利用截面惯性矩对该公式进行了进一步的优化设计，得到了梯形笼条鼠笼的刚度计算公式。宋谭等[7]将笼条等效为弧形截面梁，利用极坐标法修正了鼠笼弯曲刚度的计算公式。

虽然学者们不断地对鼠笼刚度理论公式进行优化，但理论公式仍然无法满足工程需要。为此，学者们对鼠笼进行了相关的试验研究，并且随着计算机技术的发展，有限元法也被广泛应用于鼠笼的相关研究。

徐方程[8]通过对轴承悬挂重物来模拟轴承传递给鼠笼的载荷以此来测量鼠笼的刚度，同时也对鼠笼进行了有限元分析。研究结果表明，有限元仿真得到的刚度要比试验刚度高3%～13%。彭京徽等[9,10]同样用悬挂重物的方法对鼠笼进行了测试，并且用数值仿真分析了根部倒角对刚度、应力的影响，研究表明，根部圆倒角能增加鼠笼刚度并且能有效减少应力集中。Senthilkumar[11]利用根部圆倒角能效减少应力集中的特性，通过设计圆倒角增加了鼠笼的高周疲劳寿命。Li[12]利用液压系统来实现对鼠笼进行无级加载，并利用该系统对鼠笼的刚度进行了测量，同时还对鼠笼进行了动态特性数值仿真，试验结果与数值仿真结果吻合度较高。孙彦博等[13]用ABAQUS 和ADINA 同时对鼠笼弹性支承进行了仿真，二者的最大变形量几乎一致，互相验证了准确性。

虽然众多学者利用有限元法来对鼠笼进行相关的数值分析，但鲜有学者对鼠笼数值仿真中的网格划分以及外力加载方式进行详细的研究。为此，本文对鼠笼条和根部圆倒角进行了网格无关性检验，在此基础上研究了外力加载方式对鼠笼刚度的影响，最后通过相关试验来对数值仿真进行验证。

1 鼠笼刚度的理论分析和计算

传统鼠笼刚度计算公式[3]为：

式中：n为鼠笼条数目；E为材料弹性模量；a为笼条长边长度；b为笼条短边长度；L为鼠笼条长度。

利用笼条受力方向和主弯方向不一致的特点，式(1)可被优化为[4]：

从笼条周向、径向截面惯性矩入手可以推导出带有梯形笼条的鼠笼刚度计算公[6]式：

式中：h为笼条截面高度；a为笼条矩形截面长边长度；b为笼条截面短边宽度。

将笼条等效为弧形截面梁，并利用极坐标法，则鼠笼刚度计算公式可修正为[7]：

式中：L为鼠笼条长度；E为材料弹性模量；N为鼠笼条数目；r1为鼠笼内径；r2为鼠笼外径；α为笼条两边之间的夹角和；θ为第一个笼条边与y 轴正方向之间的夹角。

2 鼠笼刚度的数值仿真

试验法能得到相对可靠的鼠笼刚度，但是需要在加工出实物后才能进行，且需要建立合理的测试工装夹具，配置高精度传感器，测试过程也会存在一定误差。

因此，工程中可利用有限元法对鼠笼刚度进行计算，有限元法可以较高精度地计算鼠笼弹性支承刚度，能够满足工程需求。

参照某型航空发动机的鼠笼弹支结构，建立了鼠笼的有限元数值计算模型，为了提高计算效率，将对鼠笼刚度影响较小的细节特征进行简化，单元类型采用六面体SOLID185 单元，鼠笼的有限元网格模型如图1所示。

图1 鼠笼网格模型

根据航空发动机中鼠笼的实际受力情况，将鼠笼分为固定端和受力端。有限元模型中，将固定端施加全约束边界条件，受力端施加外力荷载。鼠笼边界条件如图2所示。

图2 鼠笼边界条件示意图

2.1 网格无关性检验

对网格进行加密处理能有效地提高有限元计算精度，但随着网格数的不断增加，计算求解所需的时间也在不断增加。实际工程中，需要对模型的关键部位进行加密处理，而受约束、载荷影响较小的部位可以采用较为稀疏的网格，从而将有限的计算资源用到对计算结果影响较大的部位[14]。

鼠笼在受到轴承传递的径向载荷时，会产生相应的应力和应变，鼠笼应力分布如图3所示。

图3 鼠笼应力分布示意图

从图3 可发现，鼠笼在工作过程中应力主要集中在鼠笼条和根部倒角位置。因此，为了提高计算精度，需要对鼠笼条和根部倒角位置的网格进行加密处理。为了平衡计算精度和计算效率，需要对鼠笼条和鼠笼条根部倒角的网格进行加密处理和网格无关性验证。

2.1.1 鼠笼条网格无关性检验

对鼠笼条进行网格无关性检验时，将鼠笼条根部位置的倒角划分为2层网格，鼠笼承力端和鼠笼固定端用六面体网格划分，网格尺寸选择为2mm，鼠笼条网格尺寸从2mm 逐渐减小，鼠笼条网格如图4 所示。

图4 鼠笼条网格示意图

鼠笼条网格无关性检验结果如图5所示。从图5的网格无关性检验结果可以发现，当鼠笼条网格尺寸小于1.25mm 后鼠笼刚度数值仿真结果趋于稳定。为了提高后续数值仿真的准确性，鼠笼条网格尺寸均采用1mm网格。

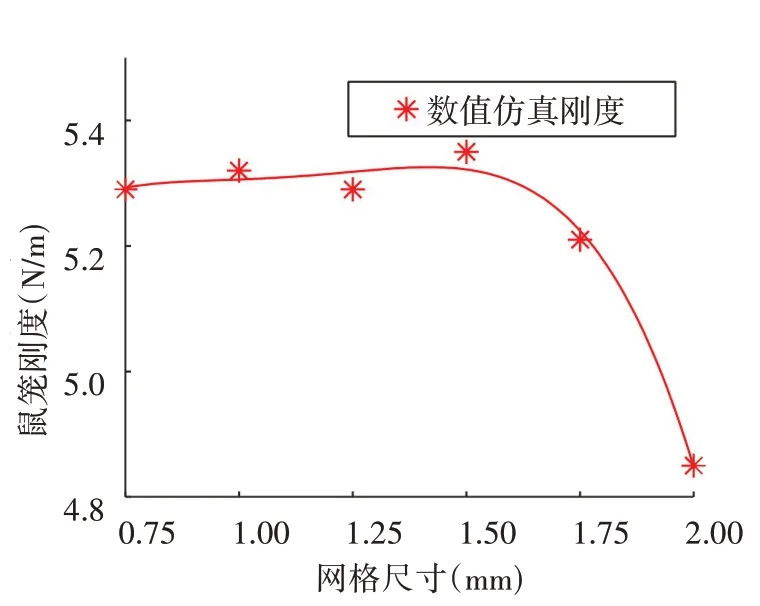
图5 鼠笼条网格无关性检验结果

2.1.2 根部圆倒角网格无关性检验

对鼠笼条根部圆倒角进行网格无关性检验时，鼠笼条网格尺寸选择为1mm，承力端和固定端部分选择用2mm 的六面体网格进行划分。鼠笼条根部网格数从一个逐渐增加，鼠笼条根部倒角网格如图6所示。

图6 根部倒角网格

鼠笼条根部倒角网格无关性检验结果如图7 所示。

图7 根部倒角网格无关性检验结果

从网格无关性检验结果可以发现，当鼠笼条根部倒角网格数大于7时，根部倒角的网格数便不再影响鼠笼的刚度。

为此，在后续的数值仿真中，鼠笼根部倒角的网格数选定为7。

2.2 外力加载方式影响分析

鼠笼在实际工作过程中受到轴承传来的径向载荷而产生变形。在数值仿真中，常用的外力加载方式有单点加载、周向多节点加载[9]、周向区域节点加载[11]以及刚性域中节点加载[8]，加载方式的不同会对鼠笼刚度的数值仿真结果产生影响。不同外力加载方式如图8所示。

图8 不同载荷加载方式示意图

外载荷加载方式为单点加力时，为了避免出现应力集中现象，需要将加载节点附近的节点与加载节点进行刚化位移协同，如图9所示。根据圣维南原理[15]，将静力用等效力系替代只会产生加载位置局部应力的改变，而对整体应力和应变几乎无影响。

图9 加载节点附近的刚性域

当加载方式为刚性域加载时，需要在承力端的中心位置建立一个无质量点，该无质量点与同轴向位置的内圈节点进行刚化位移协同操作，并在该无质量点上加载外力。采用刚性域加载时，外力加载示意图如图10所示。

图10 刚性域加载示意图

不同外力加载方式的数值仿真结果列于表1。

表1 不同加载方式数值结果对比

由表1 中数值仿真结果可知，外力加载方式对鼠笼刚度的影响较大。其中，采用单节点加载得到的鼠笼刚度最小，通过刚性域加载得到的鼠笼刚度最大。

造成这一现象的主要原因为鼠笼承力端发生变形，不同外力加载条件下，鼠笼承力端变形情况如图11所示。

图11 不同加载方式下鼠笼承力端变形结果

承力端受到外力载荷后，承力端顶部和底部的位移并不一定相等，即鼠笼承力端由正圆形变形成了近似椭圆形，文献[8]通过悬挂试验法证实了这一点。

当外载荷加载方式为单节点加力时，承力端的刚性最弱，变形最明显，从而导致使用该外载荷加载方式得到的鼠笼刚度最低。而当外力加载方式为刚性域加载时，承力端几乎不存在形变，因此得到的鼠笼刚度最大。

鼠笼弹性支承的承力端安装有轴承，轴承通常具有较大的刚度，轴承外滚道紧贴鼠笼承力端的内壁面。在轴承外滚道的影响下，鼠笼承力端在径向外力的作用下会产生整体的位移而非局部形变，因此轴承结构对鼠笼起到加强刚度的作用。为此，我们建立带轴承的数值仿真模型并研究外力加载方式对鼠笼刚度的影响。带轴承外滚道的鼠笼网格模型如图12所示。

图12 含轴承外滚道的鼠笼网格模型

对含轴承外圈的鼠笼模型进行不同外力加载方式对鼠笼刚度的影响研究，数值仿真结果列于表2。

表2 含轴承的鼠笼在不同外力加载方式下的刚度

在建模中考虑轴承后，外力加载方式对鼠笼刚度的影响大幅度减小，并且数值仿真结果贴近不考虑轴承建模时采用刚性域加载的数值仿真结果。

从以上数值仿真研究中可以发现，网格尺寸、外力加载方式和鼠笼工作状态均对数值仿真的结果有较大的影响。为了使数值仿真结果更加准确，需要根据鼠笼的实际工作状态建立正确的模型并选择合适的边界条件。

3 鼠笼刚度试验测试研究

为了测得鼠笼弹性支承的刚度，只需在鼠笼的承力端加外力，并利用传感器测量出承力端的径位移。为此设计并搭建了鼠笼弹支刚度试验测试台，如图13所示。

图13 鼠笼刚度试验测试台

试验测试过程中，通过转动加载螺母来改变加载螺杆的拉力。拉力传感器的一端与加载螺杆相连接，另一端与传力杆相连接。拉力传感器能实时记录加载螺杆的拉力F，在转动加载螺母的过程中能够实现拉力的无级加载。

传力杆为细长金属杆，具有较高的轴向刚度。传力杆一端与拉力传感器相连，一端与鼠笼相连，将加载螺杆的拉力传递到鼠笼上使鼠笼产生位移。

在鼠笼上与传力杆相对的位置安装电涡流传感器，实时记录鼠笼的径向位移x。

在测量到加载外力F和鼠笼径向位移x后，便可根据胡克定律K=F/x计算出鼠笼刚度，试验过程中使用的鼠笼结构及参数如图14 所示，关键参数列于表3。

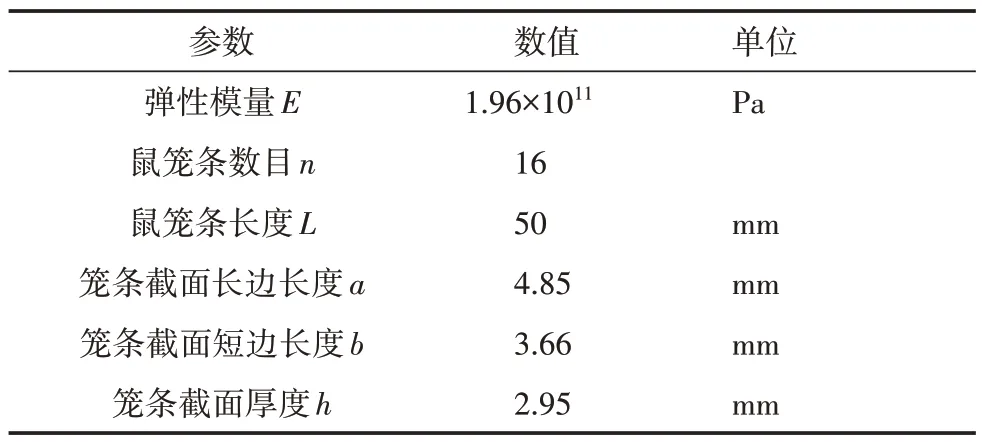
表3 鼠笼关键参数

图14 试验所用鼠笼结构及参数

根据鼠笼刚度试验台的测试特点，数值仿真时外力加载方式选择为单节点加载，并测量与加载节点成180°位置处的节点位移。边界条件设置如图15所示。

图15 鼠笼边界条件设置

鼠笼刚度的试验测试结果如图16所示。从图中可以发现，两次试验的外力—位移线的斜率基本一致，表明了两次试验测试得到的刚度基本相同，两次试验得到的鼠笼刚度平均值为3.87×106N/m。

图16 鼠笼刚度试验结果

鼠笼刚度参数化计算公式采用式(3)，用各方法计算得到的鼠笼刚度结果列于表4。

表4 鼠笼刚度计算结果

试验测试过程中，鼠笼的承力端并未安装轴承，因此，承力端在受到加载外载荷时，会产生一定的弹性形变。数值仿真中观察到鼠笼承力端产生的弹性形变如图17所示。

图17 鼠笼承力端变形数值仿真结果

由于鼠笼刚度测试试验台的特点，电涡流传感器测量的位移为鼠笼承力端的最小位移，会导致试验测试得到的鼠笼刚度略大于鼠笼的实际刚度。

数值仿真结果整体上与试验结果保持一致，在后续的转子系统设计中，可用有限元法对鼠笼刚度进行预估。参数化计算公式得到的鼠笼刚度与试验测试结果相差略大，因此不宜用于直接计算鼠笼刚度，但在鼠笼结构设计过程中，参数化计算公式能够为鼠笼设计提供方向。

4 总 结

本文对鼠笼弹性支承的数值仿真计算进行了细化研究，包括鼠笼网格模型网格无关性检验和外力加载方式的研究。研究结果表明：

(1)鼠笼条网格尺寸和鼠笼条跟部圆倒角会对鼠笼刚度的数值仿真结果产生一定的影响，为了提高数值仿真精度，需要对鼠笼条网格和根部圆倒角的网格进行网格无关性验证。

(2)外力加载方式的不同会影响鼠笼承力端的刚性，进而影响鼠笼刚度的计算值。对于航空发动机支点位置的鼠笼，轴承外滚道会限制鼠笼承力端的形变，因此在数值仿真时，考虑轴承建模后，外力加载方式对鼠笼刚度的影响减小，且数值仿真结果趋近于通过刚性域加载得到的鼠笼刚度。

(3)设计并搭建了鼠笼刚度试验台，试验台能够实现对外载荷的无级加载，并借助试验台对鼠笼刚度进行了试验测试。

(4)根据试验过程中的实际状况选择合适的边界条件，研究发现鼠笼刚度的试验测试值与数值仿真结果处于同一水平，且相对误差较小。因此，在工程实际中可以利用数值仿真来获得鼠笼的刚度。