基于信息增益优化支持向量机模型的煤矿瓦斯爆炸风险预测

万 宇, 齐金平, 张 儒, 闫 森

(兰州交通大学机电技术研究所， 兰州 730070)

目前，随着社会经济的蓬勃发展，中国已成为世界上最大的煤炭生产、消费国，安全生产已经成为一个重要现实问题[1]。煤炭行业是典型的高危行业，其事故主要包括瓦斯、顶板、底板、放炮、机电、火灾、水害、运输以及其他事故，其中瓦斯事故一般被认为是威胁性最大的灾害事故。中国高瓦斯矿井数占到了接近总量的一半，每年因瓦斯事故带来的伤亡人数不计其数，而其中瓦斯和煤尘爆炸事故占大多数[2]。煤炭的安全开采是经济增长的重要保障，“十三五”规划中国家也对能源安全和绿色生产提出了明确的要求。因此，为了响应国家号召，应将未来的工作重心从事后响应转移到预控预防，做到从根源上遏制安全事故的发生，减少人员伤亡率。

瓦斯爆炸是瓦斯事故中典型的一种，传统预测方法主要依赖专家判断，具有较强的主观性，预测精度不能达到分析任务的要求，近年来随着计算机技术的进步与发展，机器学习算法的引入极大地推动了风险预测领域的进步，田水承等[3]利用反向传播神经网络(back propagation neural network, BPNN)对掘进面瓦斯爆炸危险进行了安全评价，李润求等[4]构建了基于区间层次分析法和功效系数法结合(interval analytic hierarchy process-efficacy coefficient method, IAHP-ECM)的瓦斯爆炸灾害风险评估模型，邵良杉等[5]针对数据缺失问题将随机森林算法引入对瓦斯灾害进行预测，李爽等[6]将极限学习机与贝叶斯网络结合对风险进行预测。上述方法从不同角度对瓦斯爆炸风险预测进行了研究，机器学习的应用很大程度上提升了预测的精准度，除了各种算法上的进步，改变优化特征向量的输入也是提升速度精度的一大方向。

现将本质安全理念引入评价指标集的构建，从人、机、管理、环境四个角度构建了28个指标，并针对煤矿瓦斯爆炸灾害的特点，选取支持向量机(support vector machine，SVM)模型来进行分类预测，在此基础上选择信息增益法(information gain，IG)根据熵值优化输入变量，组成了IG-SVM的组合模型，以期能够实现对瓦斯爆炸风险的快速、高精预测。

1 分类预测模型的构建

1.1 支持向量机

支持向量机是一种基于VC维(Vapnik-Chervonenkis dimension)理论和结构风险最小化准则的监督学习算法[7]，最早起源于分类、回归领域，Vapnik[8]引入核理论，将原始低维数据映射到高维空间，在维数足够高的空间中利用超平面来进行分类，在数学上可归结为求解一个二次规划问题。SVM在面对非线性、小样本等问题时表现出色，计算复杂度取决于支持向量的数目，从而避免了“维数灾难”，并且具有良好的鲁棒性和泛化性能[9]。目前已广泛应用于计算机视觉、时间序列预测、人工智能等领域。

设样本数据集(xi,yi)(i=1,2,…,l),xi∈Rn，yi∈{-1,+1}，l为训练样本总数，n为空间的维数，xi为待分类数据，yi为标记类别，对线性可分的样本，存在一个超平面H能够将不同类的样本分开，用法向量表示其方向，H1、H2分别表示过两类样本点中与超平面H距离最近的平行平面,其间的距离称为分类间隔，在保证能够正确分类的前提下分类间隔最大的平面称为最优超平面。超平面方程为wx+b=0，d维空间中的线性判别函数为g(x)=wx+b，其中w∈Rn，w为参数向量，即超平面的法向量，b∈R为分类阈值。

归一化使|g(x)|≥1，离分类面最近的样本的|g(x)|=1，此时分类间隔为2/‖w‖，要求分类间隔最大，即要求‖w‖最小，要求所有样本分类正确，则需要满足：

yi[(wxi+b)]≥1,i=1,2,…,l

(1)

上述条件可以转化为下面带约束条件的优化问题进行求解：

(2)

样本线性可分的情况下，求解即可得到最优分类超平面，对于线性不可分的情况，存在一定的训练误差，一部分无法满足式(1)的样本数据将被视为噪声，为了给这样的噪声数据引入容错性需要在表达式中增加一个松弛变量ξi(ξi≥0)，则式(1)变成

yi[(wxi+b)]≥1-ξi,i=1,2,…,l

(3)

(4)

由此可以得到线性不可分时的最优分类超平面，称为广义分类超平面，可以表示为

(5)

(6)

式(6)中:αi为拉格朗日乘子。在处理非线性问题时，低维空间中样本数据的离群点数量非常多，引入松弛变量也无法取得较好的分类效果。根据泛函理论，只要一种核函数K=(xi,xj)满足Mercer条件，就可以代替原空间中的内积。本文拟采用的核函数有双曲正切(Sigmoid)核函数、径向基核函数(radial basis function, RBF)、线性核函数(linear kernel function, LKF)以及多项式核函数(polynomial function, PF)。利用核函数技巧后的最优分类函数为

(7)

1.2 信息增益

信息增益是一种优化特征选取的方法[10]。信息量是对信息的度量，信息的大小与随机事件的概率有关，概率越小产生的信息量越大，设离散随机变量X的概率分布为P(X=xi)=pi(i=1,2,…,n)。信息熵代表所有可能发生事件信息量的期望，也可以理解为离散随机变量的复杂度，表达式为

(8)

设有随机变量(X,Y)，其联合概率分布为P(X=xi,Y=yi)=Pij(i=1,2,…,n,j=1,2,…,m)。条件熵H(Y/X)代表在已知随机变量X的条件下随机变量Y的不确定性，表达式为

(9)

信息增益代表了在X已知的条件下，信息复杂度减少的程度，即信息熵与条件熵的差值，特征T对训练数据集D所带来的信息增益为

g(D,T)=H(D)-H(D|T)

(10)

某个特征的信息增益值越大，也就是说根据这个特征所做决定的不确定度减少越多。用这种方法可以考量特征信息对整个系统的贡献，贡献越大说明这个特征对分类决策的影响越深。

1.3 IG-SVM模型

IG-SVM模型流程如图1所示。

图1 IG-SVM模型流程示意图Fig.1 Flow diagram of IG-SVM model

模型运行步骤如下：

步骤1基于本质安全理论从人、机器、管理、环境4个方面构建瓦斯爆炸事故风险评价指标体系。

步骤2通过实际调查煤矿监控系统以及问卷调查法获取大量现场数据(包括实时数据与非实时数据)，组成原始数据集{D1,D2,…,Dm}。

步骤3将步骤2所得的原始数据集进行信息增益处理，可以获得各指标的增益值排序，选择最优指标组成新的数据集{I1,I2,…,Im}。

步骤4用mapminmax函数对数据进行归一化处理，将原始数据映射到[0,1]区间内，这样可以避免量纲不同对分类结果的影响，得到的新数据集为{G1,G2,…,Gm}，用新实验数据集训练SVM模型，重复训练优化参数后可以得到分类预测模型f(Ii)。

步骤5将未知风险的数据集导入模型训练，获得预测结果。

2 实验分析

2.1 样本的采集

瓦斯爆炸事故是煤矿特有的极其严重的一种灾害，利用事故发生与否在指标上的差异化表现可以对瓦斯爆炸风险进行预测，对事故的预控预防具有指导意义。以甘肃、山西、内蒙古自治区等地区100家中小煤矿企业为研究对象，收集他们的瓦斯爆炸事故数据，定性指标以问卷调查法获取，调查问卷向目标企业相关部门的管理人员发放。此次研究共发放问卷170份，收回141份，有效问卷为110份。对数据进行统计整理，共获得110个样本点，包括20个有风险样本(事故样本)，90个无风险样本。在此基础上，还需要对用于训练和测试的样本数据集进行划分，本文选取训练和测试的样本数量比例为8∶2，分别在有风险和无风险的样本中按比例随机抽取共88个作为预测模型的训练样本，剩下22个作为检验模型预测效果的测试样本，如表1所示。

表1 实验样本分布情况Table 1 Distribution of experimental samples

2.2 风险评价指标

本质安全是一种以事故致因论为基础的科学全面的安全理论，完全符合国家安全生产的法律法规以及“十三五”发展规划，其核心理念是从人、机器、管理、环境四个要素的角度，做到各方面协调统一，消除不安全因素，建立本质安全型企业。本文将本质安全理念结合煤矿生产的实际情况，建立了一套较为全面的指标体系，如表2所示。为达到简化SVM模型提高预测正确率的目的，通过IG模型分析输入变量，提取对瓦斯爆炸风险分类结果有显著影响的指标，影响程度以信息增益值表示，信息增益的排序结果如表3所示，本文选择信息增益值大于0.015所对应的14个特征变量组成新数据集合。

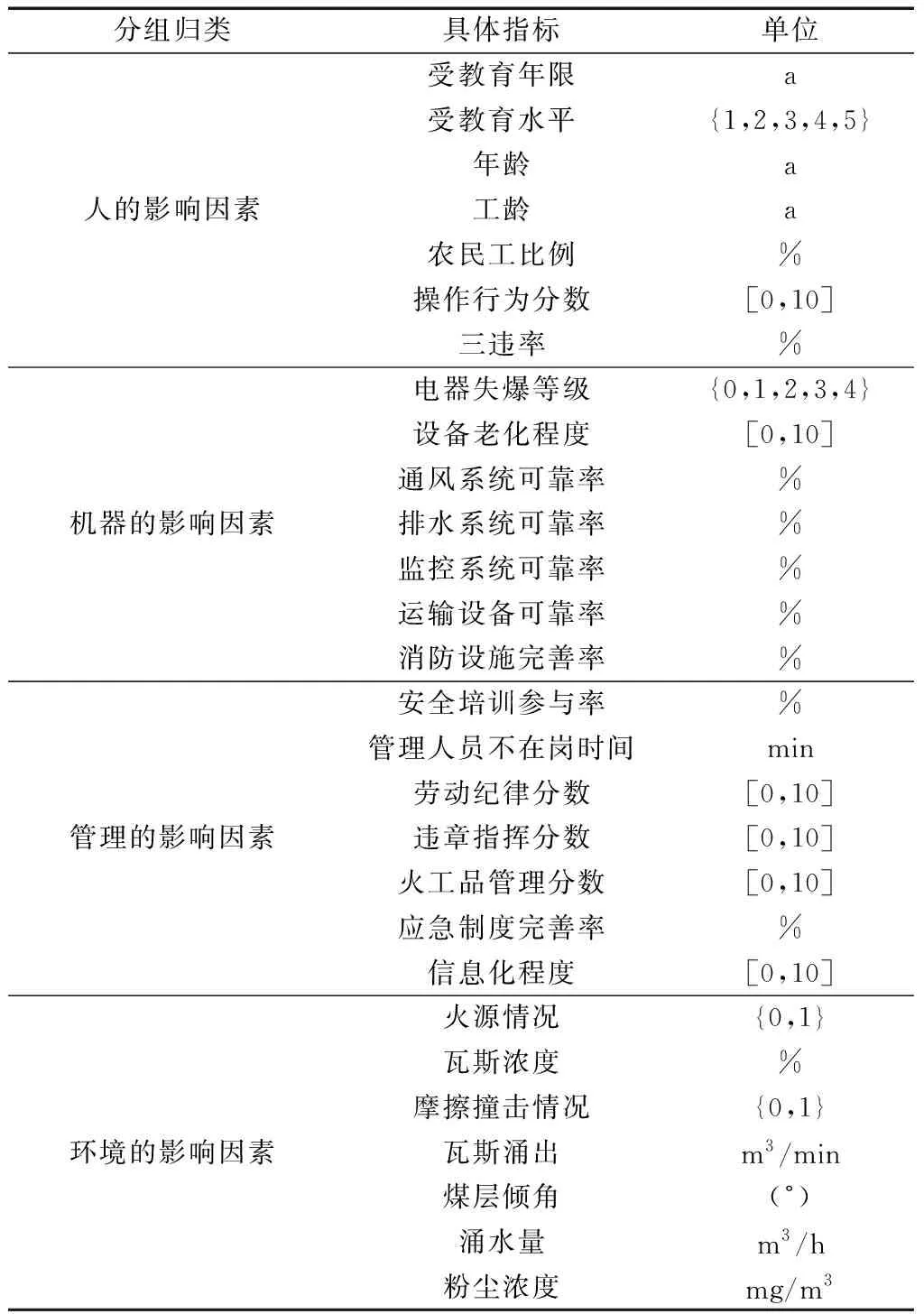
表2 瓦斯爆炸风险指标体系

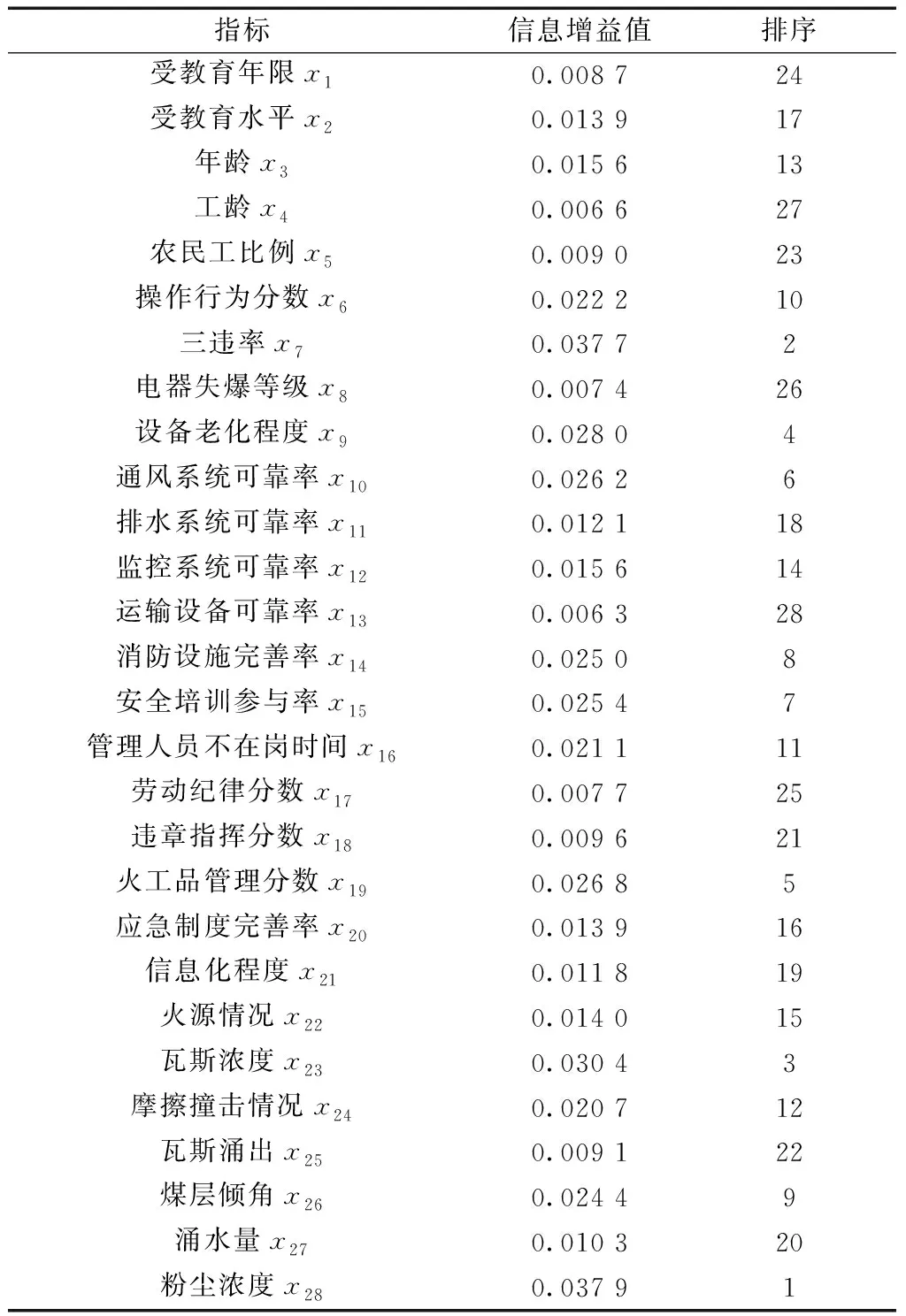
表3 特征指标信息增益排序表

2.3 参数设置及核函数的选取

本文建立的预测模型由Windows系统下的MATLAB19.0实现，采用MATLAB中的mapminmax对原始数据进行归一化，得到的新数据集与原数据集具有高度紧密性。SVM中核函数的选取对特征空间起着决定性的作用，目前还没有算法用于选取最适合核函数的方法，一般采取试凑法，本文选取最常用的4种核函数分别是：Sigmoid核函数、LKF、PF、RBF，对分类结果进行对比，选取最优的核函数，其中LKF没有需要专门设置的参数，其余参数如表4所示。

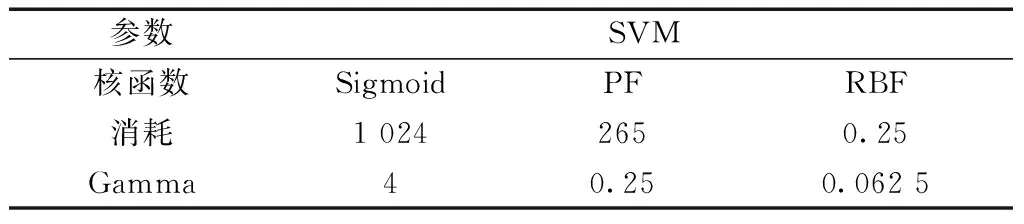
表4 核函数参数情况Table 4 Parameters of kernel function

瓦斯爆炸事故风险实际上是一个二元分类问题，即将煤矿开采区域分为两类有风险、无风险，采用混淆矩阵来评价分类模型的性能，如表5所示。

表5 混淆矩阵

P/N(positive/negative)表示预测对象的所属类别，T/F(true/false)表示分类的正确与否，例如TP即将实际有风险的煤矿预测为有风险的样本数量，利用混淆矩阵可以计算出一些评价模型性能的指标如：正确率Acc=(TP+TN)/(TP+TN+FP+FN)、准确率Precision=TP/(TP+FP)、召回率Recall=TP/(TP+FN)等[11]。以上指标虽然能够一定程度上的评价模型性能，但是应用于本文的分类器模型评价中大致有两方面的问题：一是煤矿瓦斯事故属于低概率事件，那么在收集数据时极大可能发生正负样本数量悬殊，例如事故样本数量占总量1%时，分类器只需将所有样本判定为无风险，则准确率也可达到99%，这显然是不合理的。其次风险的发生虽然是一个二元分类问题，但是所选对象归属类别的程度不同，简单地用0或1概括会导致一些信息丢失。

ROC(receiver operating characteristic)曲线也称受试者工作特性曲线，其横纵坐标分别是假阳性率(false positive rate，FPR)和真阳性率(true positive rate，TPR)，坐标(0,1)对应的是理想的分类模型，用曲线下的面积(area under curve，AUC)来表示分类器的性能，AUC的大小一般在0.5～1，越靠近1表示越接近理想分类模型。选择ROC曲线不仅能够解决前文提出的两方面问题，而且能直观地反映不同核函数模型分类情况的优劣。

将数据代入不同核函数的模型，ROC曲线如图2所示，ROC曲线越靠近左上角表示分类效果越好，为了更加准确地描述可以计算曲线下面积，即AUC值，如表6所示。

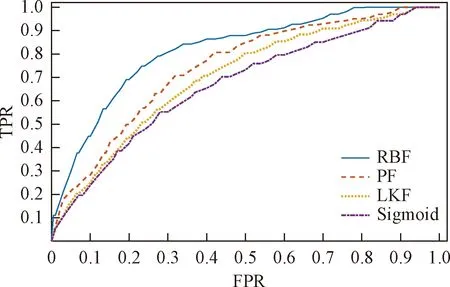
图2 模型输出的ROC曲线Fig.2 ROC curve of model output

表6 不同核函数AUC比较Table 6 Comparison of AUC values of different kernel functions

由表6可知使用RBF核函数构造的模型输出的AUC最高，而使用Sigmoid核函数、PF、LKF的构造的模型输出的AUC都在0.7～0.8，效果不甚理想且相互之间差别不大。LKF作为RBF的一种特殊形式，在实验过程中发现两种核函数差距较大，推测可能是由于煤矿瓦斯爆炸风险并不是线性可分的。Sigmoid核函数可能在某些参数下是无效的，因此给参数选取带来困难。PF的支持向量较多分布于边界处，可能对分类预测产生干扰。此外，RBF有很强的映射复杂非线性关系的能力，且学习规则简单、调试参数迅速，鲁棒性强。综上所述，本文选用RBF作为核函数建立预测模型。

2.4 结果与讨论

为了体现本文选用的IG-SVM模型的效能，将该模型的预测结果与一些常用的分类器在同样的样本条件下进行比较，为了简化比较结果，仅对预测结果作二元分类(+1表示有风险，-1表示无风险)，结果以样本的分类正确率表示，如表7所示。

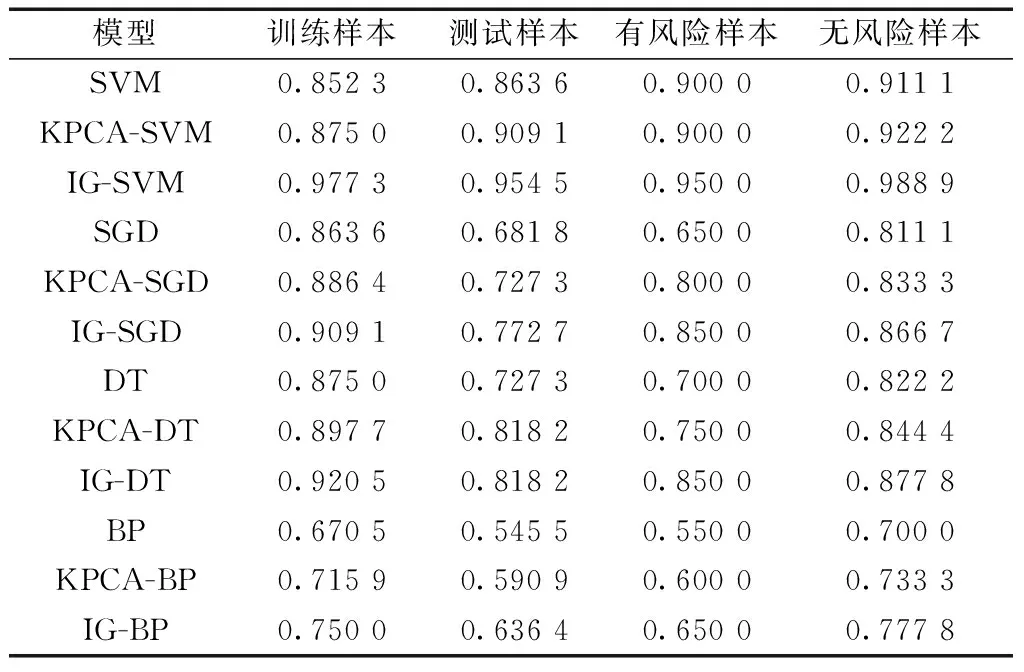
表7 各模型分类预测结果对比Table 7 Comparison of prediction results of different models

实验结果表明：在4种单一分类模型中，SVM对训练样本的分类正确率为85.23%，略低于决策树(decision tree, DT)模型和随机梯度下降(stochastic gradient descent, SGD)模型，而对测试样本的分类正确率最高，达到了86.36%，而本文建模分类的目的是预测瓦斯爆炸风险，显然测试样本的结果更加重要，在有风险样本和无风险样本中，SVM的表现要优于3种其他模型。比较使用了IG优化后的各种模型，4种分类正确率均有所提高，例如IG-SVM模型相对于SVM模型4种正确率分别提高了12.5%、9.09%、5%、7.78%，说明了经过IG特征提取后的模型分类性能有所提高。此外，实验还使用了核主成分分析法(kernel principal component analysis, KPCA)进行特征选取优化作为对比，可以看出，经过KPCA优化后的模型，虽然整体水平也有所提升，但普遍低于IG优化后的模型，充分说明了IG在特征选取优化方面的表现十分优异。

3 结论

依据本质安全理念建立了指标集，研究了IG-SVM在处理煤矿瓦斯爆炸风险预测上的表现，具体结论如下：

(1)针对煤矿瓦斯爆炸风险问题，使用SVM进行分类预测取得了不错的效果，但是过于庞大的指标体系在一定程度上形成了特征信息的冗余，从而影响计算机仿真的速度与正确率。因此，优化评价指标体系是十分必要的。

(2) IG通过对信息增益值进行排序精简指标体系，删除了不必要的冗余信息，降低了模型整体的运算维度，从而优化了模型的速度与正确率，并通过实验证明IG与SVM的组合在解决本文问题时要优于其他模型，最终测试样本的正确率达到了95.45%，在防控灾害上有很好的应用价值。