近海在役钢筋混凝土框架结构抗震能力时变劣化规律

王立波， 王伟伟

(安阳工学院土木与建筑工程学院， 安阳 455000)

中国不仅是一个地震多发国家，同时还拥有漫长的海岸线，具有广泛的近海氯离子侵蚀环境，因而，中国沿海城市中大量在役钢筋混凝土(reinforced concrete，RC)框架结构自建成之初即同时面临地震灾害和氯离子侵蚀作用的双重威胁。氯离子侵蚀作为引发RC结构内部钢筋锈蚀的首要原因[1]，不仅导致混凝土锈胀开裂，引发一系列耐久性损伤问题，还会逐步削弱钢筋的有效截面面积，破坏钢筋与混凝土界面间的黏结性能，降低保护层及箍筋约束混凝土的力学性能[2]，导致在役RC框架结构的抗震性能呈现明显的时变退化特性，然而，现有的抗震设计理论并未考虑充分这一影响。因此，随着服役龄期的增长，近海在役RC框架结构的震害风险将不断加剧，甚至可能超越社会可接受程度，带来巨大的经济损失和社会影响。

明确近海在役RC框架结构的抗震能力劣化规律是降低其震害风险的重要前提。近年来，基于大量试验研究，中外学者先后建立了多种锈蚀钢筋本构模型[3-5]、锈蚀箍筋约束混凝土本构模型[6-7]及锈蚀RC框架梁、柱、节点的时变恢复力模型和数值模拟分析方法[8-11]，有效推动了在役RC框架结构抗震性能研究进程。然而，由于上述研究成果大多停留在材料或构件层面，且未与结构的服役龄期产生联系，因而无法有效表征整体结构的抗震能力时变劣化规律。为此，郑山锁等[12]、刘小娟等[13]分别基于氯离子扩散理论预测钢筋锈蚀程度，采用数值模拟分析方法，开展了氯盐侵蚀条件下在役RC框架结构的抗震性能研究，并探讨了其地震易损性、承载能力、变形能力、耗能能力等抗震性能指标随服役龄期的变化规律。然而，由于采用的抗震性能指标并未直观反映结构的实际抗震能力，因此，近海在役RC框架结构的抗震能力时变劣化规律仍未得到有效的量化表征。

实际上，结构的抗震能力从概念上可表示为其特定破坏状态下可抵御的地震强度。基于此，现介绍近海在役RC框架结构的数值建模方法，进而以可抵御的地震动峰值加速度(peak ground acceleration，PGA)表征其抗震能力，建立基于能力谱方法的在役RC框架结构抗震能力量化方法，并分析不同设防水平在役RC框架结构不同破坏极限状态的抗震能力劣变规律，给出理论表征，以期为近海在役RC框架结构的抗震性能评估提供参考。

1 近海在役RC框架结构建模方法

相对新建结构而言，近海在役RC框架结构数值建模的关键在于，确定结构不同服役龄期下的钢筋锈蚀深度，模拟锈蚀钢筋、锈胀开裂保护层混凝土、锈蚀箍筋约束混凝土的力学行为以及锈蚀钢筋混凝土的黏结滑移行为。

1.1 钢筋锈蚀深度预测模型

锈蚀后钢筋的截面削弱可以采用钢筋锈蚀深度直观量化表征。当假定钢筋均匀锈蚀时，不同服役龄期t时在役RC结构中钢筋的锈蚀深度δc(t)可以表示为

(1)

式(1)中：Tcor为钢筋初始锈蚀时间；λ(t)为钢筋的时变锈蚀速率，其可以通过腐蚀电流密度icor(t)按式(2)、式(3)[14]计算确定，即

λ(t)=0.011 7icor(t)

(2)

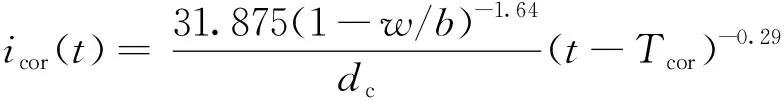
(3)

式中：w/b为混凝土的水胶比；dc为混凝土的保护层厚度。

据此，将式(2)和式(3)代入式(1)，推导得出不同服役龄期t时在役RC框架结构中钢筋的锈蚀深度δc(t)计算模型为

(4)

式(4)中：Tcor为钢筋的初始锈蚀时间。氯离子侵蚀条件下，钢筋表面氯离子浓度达到致使钢筋脱钝的临界浓度时，钢筋随即脱钝开始锈蚀，因此，根据Duracrete[15]提出的氯离子扩散理论模型，考虑混凝土水化进程对氯离子扩散速率的影响，可以得到钢筋初始锈蚀时间的计算模型[15]为

(5)

式(5)中：dc为混凝土保护层厚度；erf-1(·)为误差函数的反函数；ke、kt、kc分别为环境影响、试验方法和养护条件修正系数；D0为混凝土龄期为t0=28 d时的氯离子扩散系数；n为时间衰减系数；Cs为混凝土表面的氯离子浓度。

为考虑上述参数变异性及其耦合作用对钢筋起锈时间的影响，取C30、C35、C40混凝土的水胶比w/b为0.46、0.42、0.38，氯离子扩散系数D0为189.77、252.01、345.97 m2/a，结合文献[15]给定的近海大气区其余各参数的概率分布模型，通过10 000次Monte-Carlo抽样考虑式(5)中各参数的变异性影响，计算得到不同水胶比、不同混凝土保护层厚度下钢筋初始锈蚀时间的概率分布，结果如图1所示。

由图1可以看出，不同设定工况下钢筋初始锈蚀时间的概率分布基本符合对数正态分布(拟合优度R2均大于0.95)，因此，采用对数正态分布函数对图1所示的抽样结果进行参数拟合，得到不同水胶比、不同混凝土保护层厚度下钢筋初始锈蚀时间的均值Tcor,m和标准差ε，如表1所示。据此，根据式(4)计算得到不同水胶比、不同混凝土保护层厚度下钢筋的平均锈蚀深度随服役龄期的变化情况，结果如图2所示。

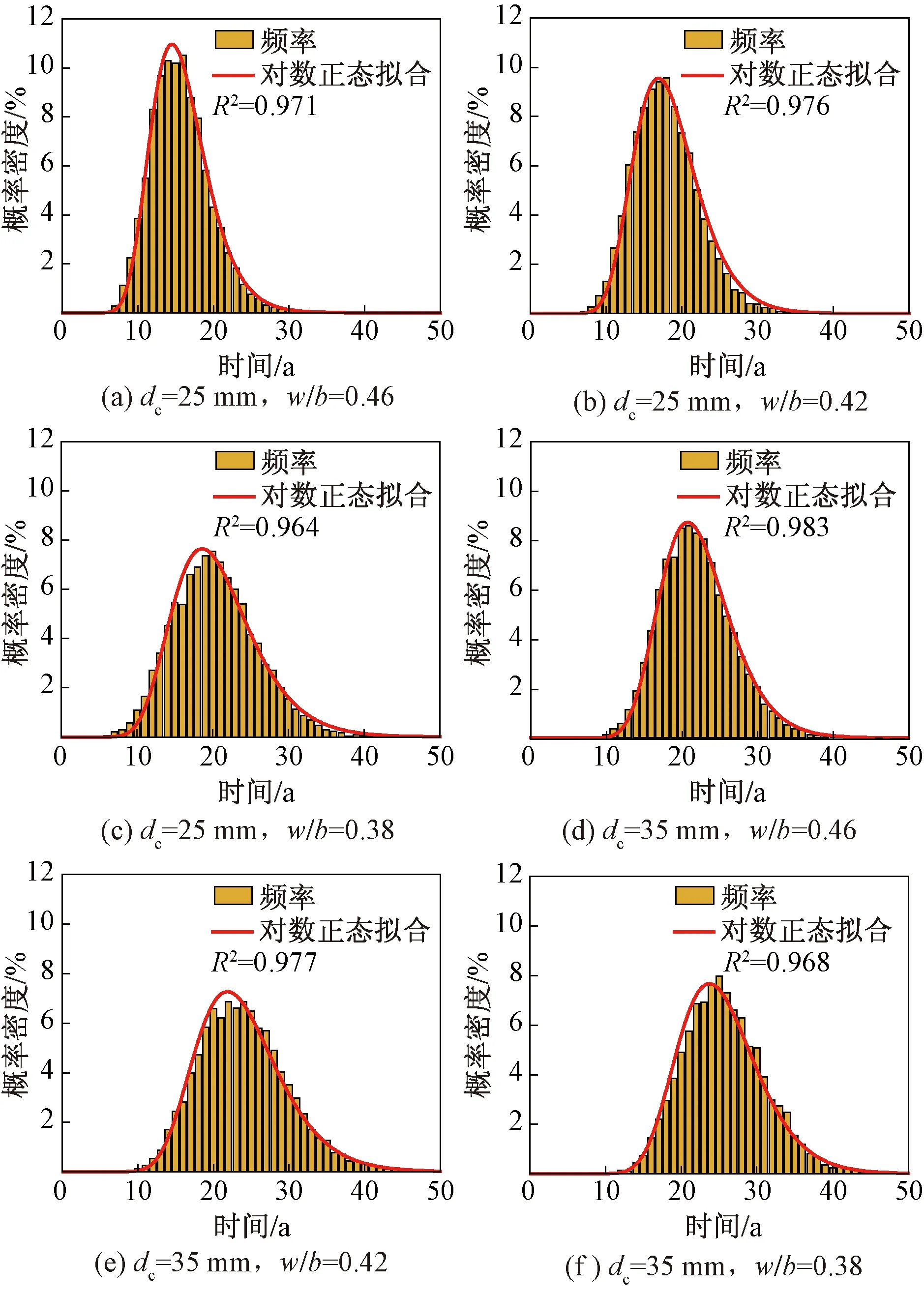
图1 钢筋初始锈蚀时间概率分布模型Fig.1 Probability distribution model of reinforcement initial corrosion time

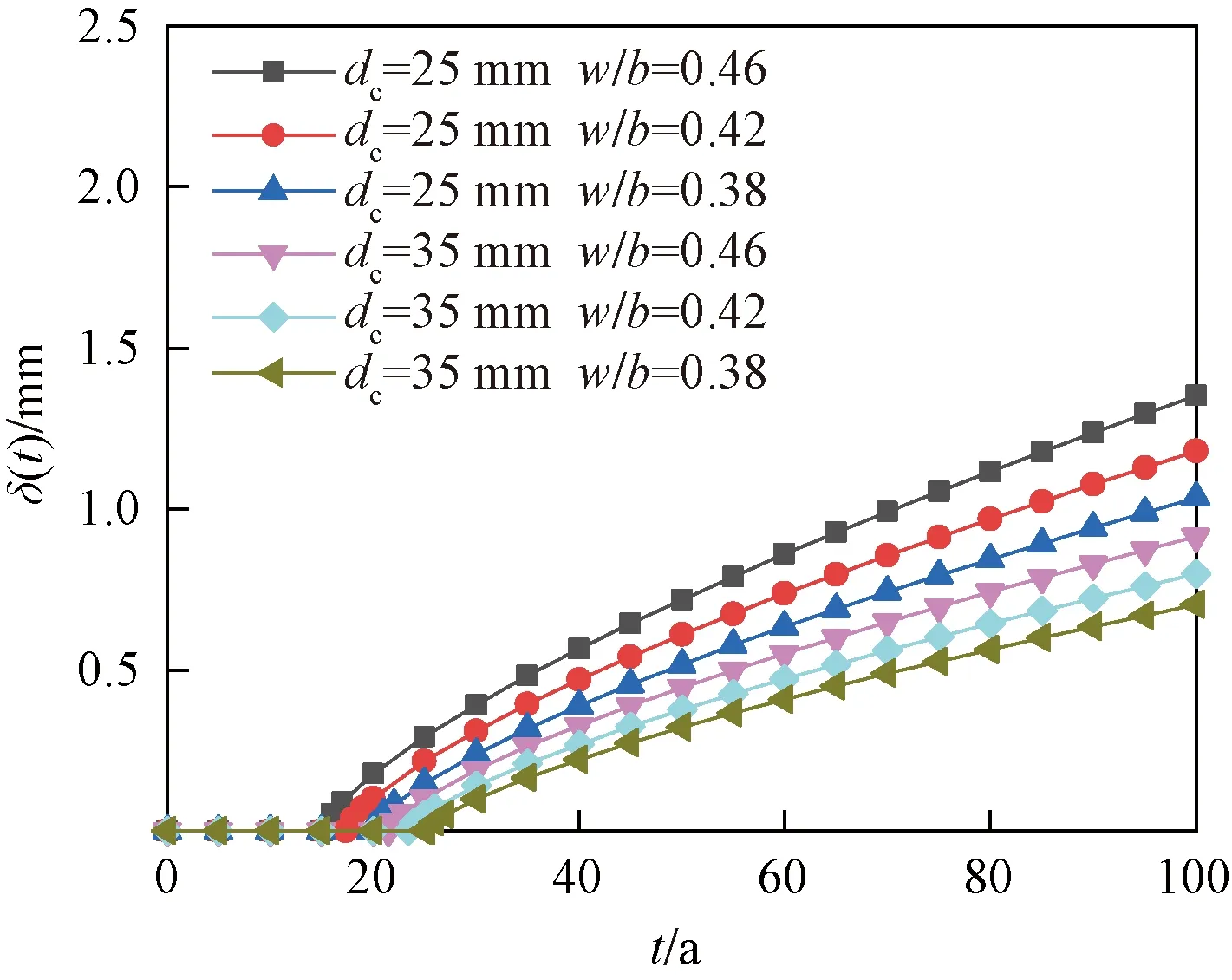
图2 钢筋平均锈蚀深度时变曲线Fig.2 Time-varying curve of average corrosion depth of reinforcement

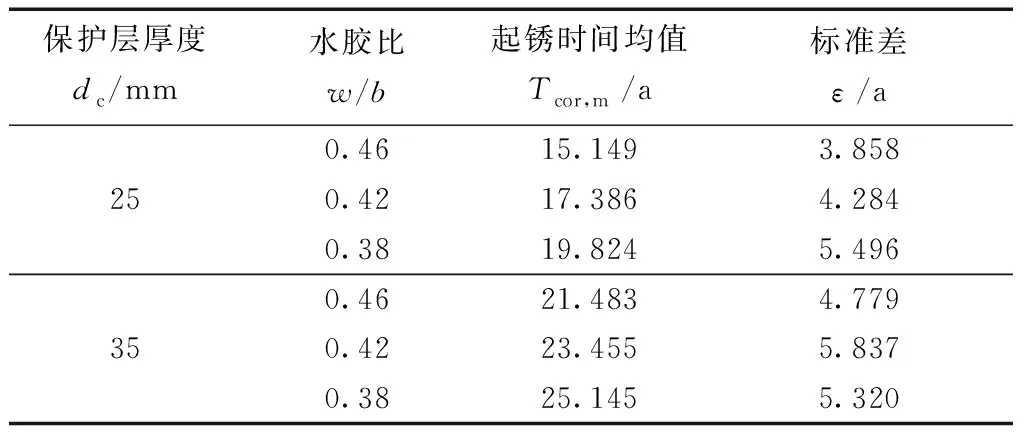
表1 钢筋起锈时间均值与标准差

1.2 锈蚀钢筋力学性能模拟

既有研究表明[3-5]，锈蚀钢筋的弹性模量、屈服强度、极限强度等力学性能指标均随钢筋锈蚀程度

的增加而不断退化。然而，上述研究结论实际上反映的是锈蚀钢筋名义力学性能的退化规律，未考虑锈蚀钢筋的截面面积削弱。罗小勇等[5]通过三维扫描实物反求技术，获取钢筋锈蚀形态，并通过模拟分析指出，锈蚀钢筋的力学性能并未退化，其力学性能的退化，实质上是由钢筋截面面积削弱引起的。因此，建立近海在役RC框架结构数值模型时，采用未锈蚀钢筋的本构模型模拟钢筋力学性能，并通过削弱钢筋截面面积反映锈蚀钢筋的力学性能退化，其中，锈蚀钢筋的有效截面面积Acor计算公式为

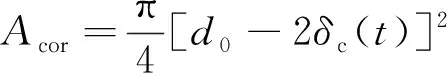
(6)

式(6)中：d0为未锈蚀钢筋的直径；δc(t)为服役龄期t时RC框架结构中钢筋的锈蚀深度，按1.1节所述方法计算确定。

1.3 锈蚀钢筋锚固滑移模型

钢筋锈蚀引发的黏结性能退化将加剧钢筋锚固滑移效应，导致在役RC框架结构中梁柱构件产生明显的附加变形，从而影响整体结构的抗震性能。潘志宏等[16]结合锈蚀钢筋的拔出试验结果及未锈蚀钢筋的锚固滑移计算模型，建立了锈蚀钢筋锚固滑移计算模型，并验证了其准确性。采用该模型模拟锈蚀钢筋的锚固滑移行为，其中，钢筋屈服时的锚固滑移量sy,c为

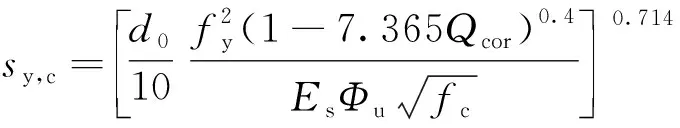
(7)

式(7)中：fy、Es分别为未锈蚀纵筋的屈服强度和弹性模量；Φu=(1-Ku)Qcor为黏结强度退化系数，其中，Qcor为钢筋锈蚀率，取Qcor=Acor/A0，A0为未锈蚀钢筋截面面积，Acor为锈蚀钢筋截面面积，按式(6)计算确定；Ku=10.544-1.586(dc/d0)，其中，d0、dc分别为纵筋直径及其保护层厚度。

1.4 钢筋锈蚀后混凝土力学性能模拟

混凝土力学性能的退化也是导致在役RC框架结构抗震性能劣化的重要因素之一。理论上，保护层混凝土力学性能的退化是由钢筋锈胀力引发的混凝土内部微裂缝开展引起的，而核心区约束混凝土力学性能的退化是由箍筋截面面积减小削弱了其对核心区混凝土的约束作用引发的。

基于上述认识，郑山锁等[12]采用开裂混凝土抗压强度计算模型，给出了锈胀保护层混凝土的力学性能参数计算方法，并通过减小箍筋截面面积，考虑箍筋约束作用削弱对核心区混凝土力学性能的影响，给出了锈蚀箍筋约束混凝土力学性能的简化计算方法。借鉴郑山锁等[12]的研究成果，并结合式(6)给出的锈蚀钢筋截面面积计算方法，标定在役RC框架结构中保护层混凝土和箍筋约束混凝土的力学性能参数，其具体标定方法参见文献[12]。

1.5 模型的建立与验证

为验证上述建模方法的准确性与合理性，基于OpenSEES有限元分析软件，采用基于刚度法的纤维梁柱单元对文献[17]中的3榀锈蚀平面RC框架结构的拟静力试验进行数值模拟。其中，钢筋本构模型采用Steel02，并通过削弱截面面积考虑钢筋锈蚀的影响；保护层及箍筋约束混凝土本构模型采用Concrete04，并按1.5节所述方法标定其力学性能参数。同时，为考虑钢筋锚固滑移效应影响，数值建模过程中，分别在构件端部添加零长度截面单元zeroLengthSection，其内部钢筋采用Bond_SP01模型模拟钢筋锚固滑移，并按1.3节所述方法标定模型参数，混凝土本构模型同样采用Concrete04。3榀锈蚀平面RC框架结构的数值模拟与试验结果对比如图3和表2所示。

由图3和表2可以看出，除再加载段曲线误差导致模拟耗能能力明显大于试验结果外，各试件模拟滞回曲线的骨架曲线、卸载刚度、强度退化等均与试验结果吻合较好，其屈服、峰值、极限状态下的承载力误差均未超过10%，相应状态的变形误差亦未超过18%，表明采用的数值模拟方法可较好模拟锈蚀RC框架结构的力学行为，可用于近海在役RC框架结构抗震能力分析。

表2 滞回曲线特征参数模拟结果与试验结果对比

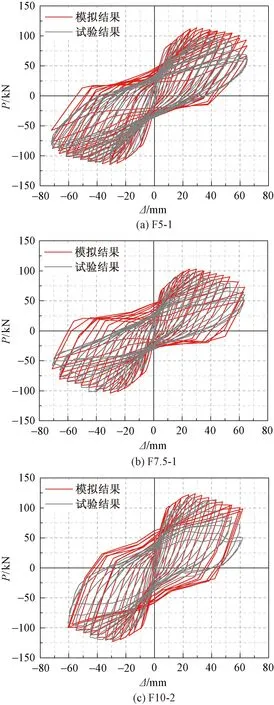
图3 水平载荷-位移数值模拟结果验证Fig.3 Load-displacement verification of numerical simulation results

2 在役RC框架结构抗震能力量化方法

2.1 基本原理

结构的抗震能力从概念上可以表示为其在特定破坏极限状态下可抵御的地震强度。在性能化抗震设计理念下，当以PGA表征地震强度时，结构的抗震能力可进一步表示为其轻微、中等、严重及近倒塌破坏极限状态下可抵御的地震动峰值加速度。因此，量化在役RC框架结构抗震能力的关键在于判别其不同破坏极限状态下可抵御的地震动峰值加速度PGA。

地震作用下，在役RC框架结构的动力响应基本受一阶模态控制，因此，基于Pushover分析方法可以将多自由度的在役RC框架结构转化为与之等效的单自由度体系。

Sa=Apgβ

(8)

式(8)中：β为弹性单自由度体系规则化的地震动动力放大系数，其计算公式为

(9)

相应的，对于与该单自由度体系相似的弹性周期为T、延性为μ的弹塑性单自由度体系，根据弹塑性需求谱的相关研究成果可知[18]，其谱加速度Sap可表示为

(10)

将式(8)带入式(10)，可得

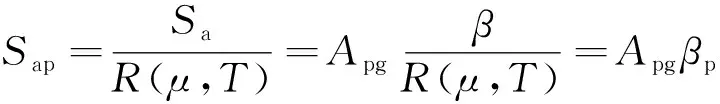
(11)

式(11)中：R(μ,T)为弹塑性谱加速度相对弹性谱加速的折减系数；βp为弹塑性单自由度体系规则化的地震动动力放大系数。

式(8)和式(11)表明，通过Pushover分析方法，将多自由度的框架结构转化为等效单自由度体系，并给定不同破坏极限状态的谱加速度Sai与动力放大系数βi后，其相应破坏状态下可抵御的地震动峰值加速度Ai可按式(12)计算确定：

(12)

式(12)中：βi实质上是规则化地震动作用下结构的弹性或弹塑性加速度响应，可根据平滑后的弹性动力系数谱曲线，及经R-μ-T格式的强度折减模型[18]折减弹性动力系数谱曲线得到的弹塑性动力系数谱曲线计算得到。

2.2 具体量化方法

基于上述原理，建立了基于能力谱方法的在役RC框架结构抗震能力量化方法，其具体分析步骤如下。

步骤1采用与一阶模态惯性力Mφ成比例的侧力模式对结构进行Pushover分析，获取其基底剪力V与顶点位移Δ的关系曲线(Pushover曲线)，并转换为谱加速Sa和谱位移Sd格式，得到在役RC框架结构的能力谱曲线，如图4所示。

步骤2采用混合控制原则[19]，确定结构不同破坏极限状态下的基底剪力Vi和顶点位移Δi，并转化为相应的谱加速度Sai和谱位移Sdi，结果如图4所示。其中，轻微、中等、严重破坏极限状态分别按首个构件屈服、Pushover曲线等效屈服及基底剪力达到峰值定义[19]；同时，考虑到Pushover分析不适于识别结构倒塌的动力失稳特性，将Pushover曲线中基底剪力降低至峰值剪力85%所对应的点定义为结构的近倒塌破坏极限状态。

步骤3计算结构不同破坏极限状态的动力放大系数βi。βi实质上是规则化地震动作用下结构的弹性或弹塑性加速度响应，其与结构不同破坏极限状态的等效周期Tei密切相关。由能力谱法[18]的基本原理可知，结构不同破坏极限状态的特征点实际上是特定地震动强度的弹性或弹塑性需求谱与结构能力谱曲线的交点(图4)，同时，需求谱的谱加速度Sa与谱位移Sd存在式(13)所示的关系，因此，根据交点处需求谱与能力谱曲线的割线刚度相等，可以得到结构不同破坏极限状态的等效周期Tei计算公式，即

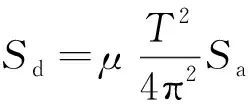
(13)

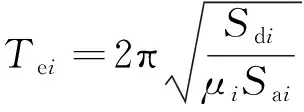
(14)

式中：μi为结构不同破坏极限状态谱位移Sdi与等效屈服点谱位移Sdy(其值等于中等破坏极限状态的谱位移Sdm)的比值，当μi<1时，取μi=1，此时弹塑性需求谱转化为弹性需求谱。

由式(14)计算得到结构不同破坏状态的等效周期Tei后，代入式(15)和式(16)，即可得到结构相应破坏极限状态的动力放大系数βi。

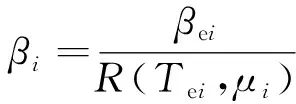
(15)

(16)

式中：R(Tei,μi)为Fajfar等[18]建立的强度折减模型；Tg为场地特征周期，当μi<1时，取Tg=1；βei为等效周期Tei对应的弹性动力放大系数，其与周期的关系可根据中国抗震设计规范给出的地震影响系数谱曲线反推得到。

步骤4量化结构不同破坏极限状态可抵御的地震动峰值加速度PGA。将步骤2～步骤3确定的结构不同破坏极限状态的谱加速Sai与动力放大系数βi代入式(12)，计算得到结构轻微、中等、严重和近倒塌破坏极限状态可抵御的地震动峰值加速度As、Am、Ae、Ac。特定服役龄期RC框架结构的抗震能力量化方法示意图如图4所示。

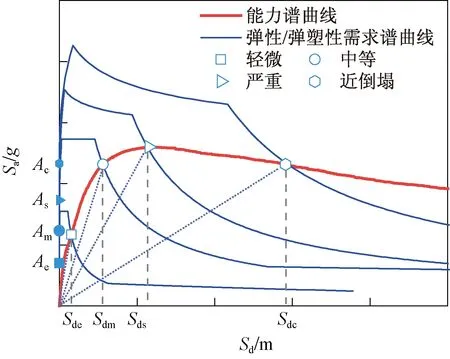
图4 抗震能力量化方法示意图Fig.4 Schematic diagram of seismic capacity quantification method

3 算例分析

3.1 算例结构设计与服役龄期设定

依据中国现行设计规范，采用图5所示的平立面布置形式，分别设计5个不同设防水平的5层RC框架结构作为算例结构，其设计参数为：建筑类别为丙类，设计地震分组为第二组，场地类别为Ⅱ类；楼面恒荷载标准值为5.5 kN/m2，活荷载标准值为2.0 kN/m2；屋面恒荷载标准值为6.5 kN/m2，活荷载标准值为2.0 kN/m2；基本风压为0.4 kN/m2，地面粗糙类别为C类；基本雪压为0.3 kN/m2；各算例结构的设计混凝土强度等级为C40，纵筋强度等级为HRB400，箍筋强度等级为HPB300；各构件的混凝土保护层厚度均为25 mm，楼、屋面板厚均为120 mm。最终设计得到各算例结构计算平面框架的梁、柱构件截面尺寸及其一阶周期与弹性最大层间位移角如表3所示。

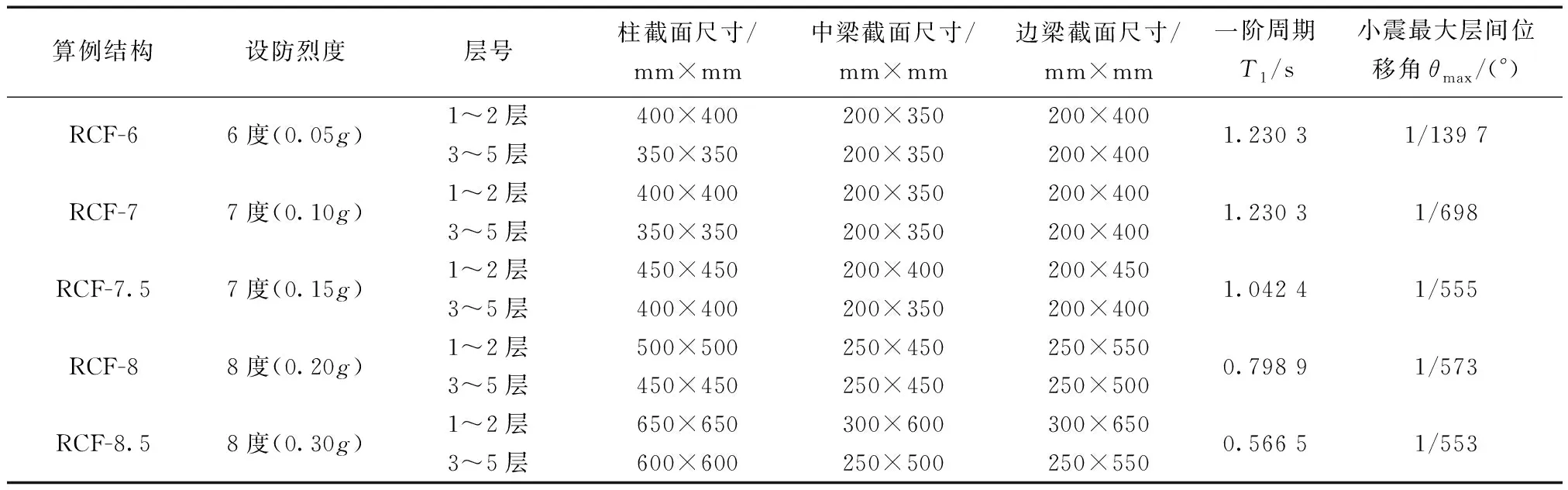
表3 算例结构的构件截面尺寸及抗震设计结果

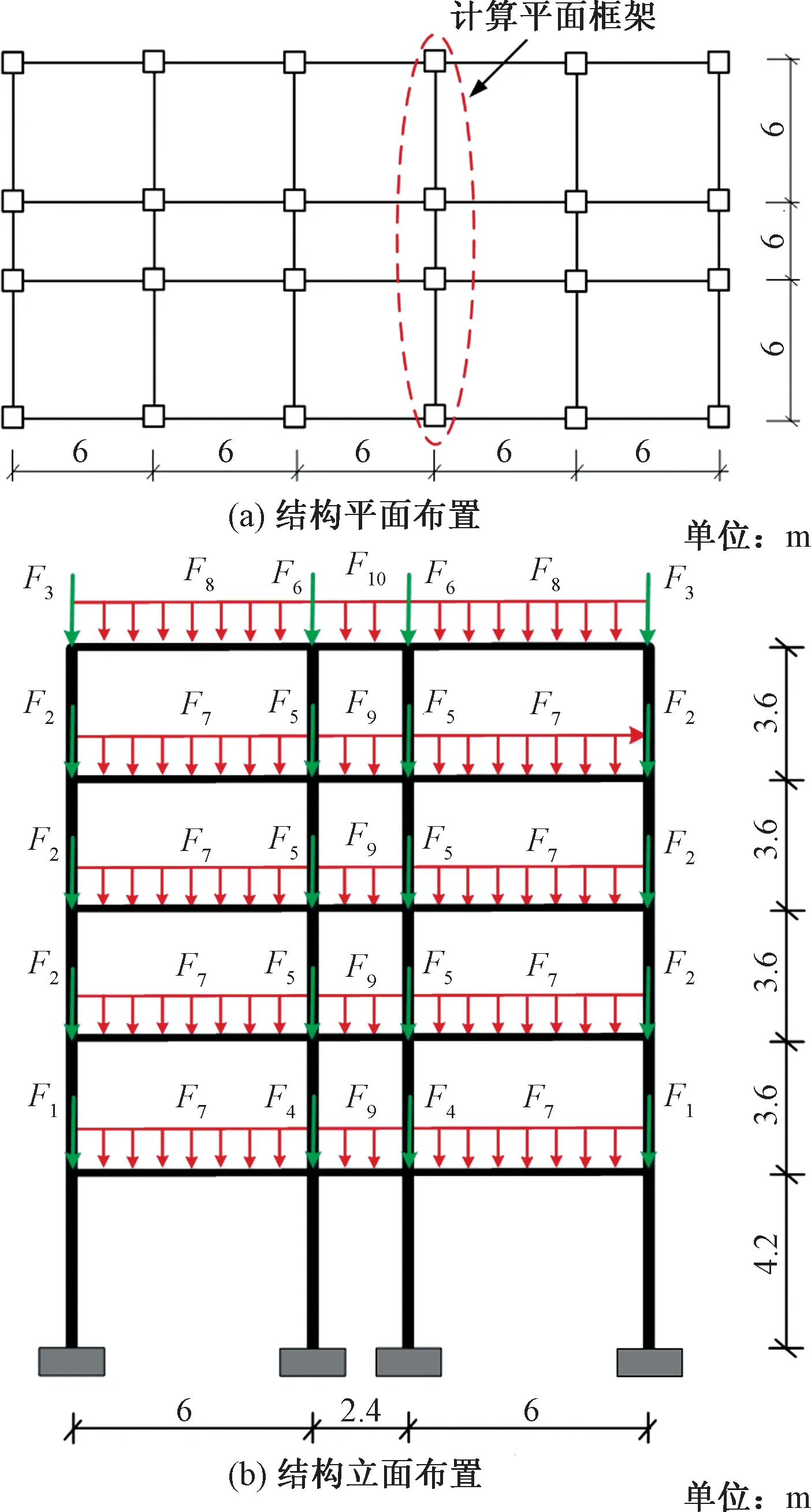
图5 算例结构的平立面布局Fig.5 Plane and elevation layout of example structures

算例结构设计完成后，为揭示其抗震能力时变劣化规律，需建立其不同服役龄期的数值模型。理论上，在役RC框架结构抗震能力为关于服役龄期的连续函数，但时间间隔太短，其抗震能力变化有限。此外，图2表明，当近海在役RC框架结构的服役龄期小于20 a时，其内部钢筋并未发生明显锈蚀；大于20 a时，钢筋锈蚀深度不断加剧。因此，为准确捕捉近海在役RC框架结构全寿命周期的抗震能力劣化规律，设定在役RC框架结构的服役龄期如表4所示。在此基础上，分别取箍筋和纵筋的保护层厚度为25 mm和35 mm，C40混凝土的水胶比为0.38，由1.1节建立的钢筋锈蚀深度预测模型，计算得到各算例结构不同服役龄期下箍筋和纵筋的平均锈蚀深度如表4所示。

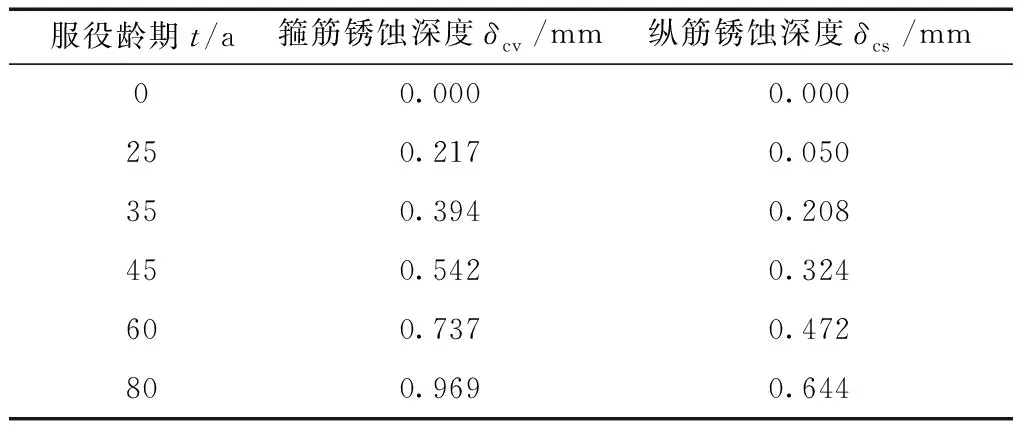
表4 不同服役龄期下钢筋平均锈蚀深度

3.2 在役RC框架结构Pushover分析

设定服役龄期并计算得到相应龄期下箍筋和纵筋的平均锈蚀深度后，按照第1节所述的建模方法，分别建立不同服役龄期下各算例结构的数值模型，并采用与一阶模态惯性力Mφ成比例的侧力模式对模型进行Pushover分析，得到算例结构不同服役龄期下的Pushover曲线，如图6所示。

由图6可以看出，相同设防水平、不同服役龄期RC框架结构的初始刚度基本不变，其轻微破坏极限状态下的基底剪力(V)和顶点位移(Δ)亦无明显区别。但超过轻微破坏极限状态后，不同服役龄期RC框架结构的抗侧刚度，以及中等、严重、近倒塌破坏极限状态的基底剪力(V)和顶点位移(Δ)均发生了不同程度的退化，且其退化程度随着服役龄期的增加不断增大。这一现象表明，服役龄期的增长对在役RC框架结构弹性阶段的力学性能及轻微破坏的发生并无明显影响，但其显著降低了结构中等、严重、近倒塌破坏极限状态的承载和变形能力，导致结构相应破坏状态的发生不断提前。

此外，对比相同服役龄期、不同设防水平RC框架结构严重、近倒塌破坏极限状态下基底剪力的退化程度可以看出，高设防水平结构严重和近倒塌破坏极限状态的基底剪力退化速率有所减缓，具体表现为：6度设防结构在服役45、60、80 a后，其严重和近倒塌破坏极限状态下的基底剪力分别降低了8.17%、11.30%和14.89%，而8.5度设防结构在相同服役龄期下，相应破坏极限状态的基底剪力仅降低了3.59%、6.29%和9.72%。分析其原因为：在役RC框架结构严重、近倒塌破坏极限状态的基底剪力劣化程度与其纵筋截面面积削弱程度密切相关；相同服役龄期下，不同设防水平RC框架结构中纵筋锈蚀深度相当，但低设防水平结构的钢筋直径较小，相同锈蚀深度下，其截面面积削弱程度较大，因而其严重和近倒塌破坏极限状态的基底剪力退化程度较大。

另外，由图6还可以看出，相同龄期下，低设防水平RC框架结构的延性明显低于高设防水平RC框架结构的延性，其原因在于：低设防水平RC框架结构的柱截面尺寸由轴压比控制，而高设防水平RC框架结构的柱截面尺寸由小震下的最大层间位移角限值控制，因而低设防水平RC框架结构的柱轴压比较大；较高轴压比下，RC框架柱的延性较差，因此，低设防水平RC框架结构的延性亦较差。式(15)表明，结构的不同破坏极限状态的动力放大系数βi与结构的延性密切相关，因此，研究近海在役RC框架结构的抗震能力劣化规律时，应综合考虑设防水平变化的影响。

3.3 在役RC框架结构抗震能力劣化规律

基于上述Pushover分析结果，采用第2节建立的抗震能力量化方法，分别计算设定服役龄期下各算例结构轻微、中等、严重、近倒塌破坏极限状态下可抵御的地震动峰值加速度As、Am、Ae、Ac，结果如表5所示。

表5 设定服役龄期下算例结构不同破坏极限状态的抗震能力量化结果

由表5可以看出：随着服役龄期的增长，RC框架结构各破坏极限状态的抗震能力均发生了一定程度的退化，但其不同破坏极限状态下的退化程度不同。以8度设防结构为例，当服役龄期达到80 a时，其轻微、中等、严重、近倒塌破坏极限状态下可抵御的地震动强度相对新建结构分别退化了5.52%、7.72%、10.92%和14.44%，其余设防水平结构具有类似的退化规律。这一现象表明，服役龄期的增长对在役RC框架结构严重和近倒塌破坏状态的抗震能力影响更为显著。考虑到结构严重、近倒塌破坏的震害后果相对轻微和中等破坏更为突出，因此，评估在役RC框架结构抗震性能时，应合理考虑服役龄期的影响。

此外，对比相同服役龄期、不同设防水平RC框架结构各破坏极限状态抗震能力的退化程度还可以看出，相同服役龄期下，低设防水平RC框架结构各破坏极限状态的抗震能力退化程度相对高设防水平结构明显提升。其中，6度设防RC框架结构服役45、60、80 a后，其近倒塌破坏极限状态的抗震能力分别降低了13.39%、17.57%和22.45%，而相同服役龄期下，8.5度设防RC框架结构近倒塌破坏极限状态的抗震能力则分别降低了7.88%、10.43%和14.85%。该现象同样是由低设防水平RC框架结构中钢筋直径较小，相同钢筋锈蚀深度下，其截面面积削弱较大引起的。

综上，近海在役RC框架结构的抗震能力劣化规律同时受服役龄期与设防水平影响，且其不同破坏状态下的劣化程度不同，因此，建立近海在役RC框架结构的时变抗震能力量化模型，应综合考虑服役龄期与设防水平变化影响，并针对不同破坏状态，分别建立量化模型。

3.4 时变抗震能力量化模型

表5给出的抗震能力量化结果实际上是算例结构各破坏极限状态的绝对抗震能力，其与诸多结构设计参数有关，无法直观反映在役RC框架结构的抗震能力劣化规律。鉴于此，为建立在役RC框架结构的时变抗震能力量化模型，将表5中各算例结构设定服役龄期下不同破坏极限状态的绝对抗震能力，分别除以相应破坏极限状态下新建结构的绝对抗震能力，得到不同设防水平在役RC框架结构各破坏极限状态抗震能力退化系数(Ki)与服役龄期(t)的相关关系如图7所示。考虑到在役RC框架结构服役龄期小于20 a时，其内部钢筋基本未发生锈蚀，因此，将其服役龄期20 a时的抗震能力退化系数假定为1，并绘于图7中。

图7 抗震能力退化系数时变规律Fig.7 Time-varying law of degradation coefficient of seismic capacity

由图7可以看出，服役龄期超过20 a后，在役RC框架结构不同破坏极限状态的抗震能力退化系数Ki随着服役龄期t的增长近似呈线性关系退化，且其退化速率随设防水平的提高不断降低。鉴于此，将服役20 a后在役RC框架结构不同破坏极限状态的时变抗震能力量化模型，定义为关于服役龄期t和抗震设防烈度I的一次函数，并考虑服役龄期小于20 a时，抗震能力无明显退化的特征，采用式(17)所示的分段函数，建立相应的量化模型。

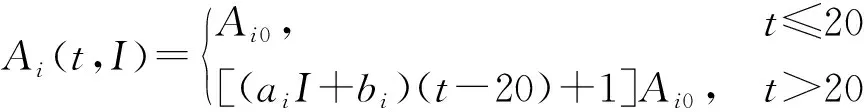
(17)

式(17)中：Ai(t,I)为服役龄期t年时设防烈度为I的在役RC框架结构不同破坏极限状态可抵御的地震动强度PGA，即其不同破坏极限状态的抗震能力，g；Ai0为新建RC框架结构不同破坏状态的抗震能力，g；I为结构的抗震设防烈度，取其基本设防烈度对应的地震动强度为代表值，其取值范围为0.05g～0.30g；ai、bi为拟合参数。

通过多参数回归分析，拟合得到服役龄期t超过20 a后，在役RC框架结构不同破坏极限状态下ai、bi的取值，从而建立了在役RC框架结构不同破坏极限状态的时变抗震能力量化模型，其结果如式(18)～式(22)所示。

轻微破坏极限状态：

As(t,I)=[10-3×(0.48I-1.08)(t-20)+1]As0

(18)

中等破坏极限状态：

Am(t,I)=[10-3×(5.17I-2.66)(t-20)+1]Am0

(19)

严重破坏极限状态：

Ae(t,I)=[10-3×(7.56I-3.44)(t-20)+1]Ae0

(20)

近倒塌破坏极限状态：

Ac(t,I)=[10-3×(6.27I-4.16)(t-20)+1]Ac0

(21)

式中：服役龄期t的取值应大于20 a。其中，轻微、中等、严重、近倒塌破坏极限状态量化模型的拟合优度R2分别为0.889、0.911、0.967、0.946，表明在役RC框架结构的抗震能力退化与服役龄期和设防水平的变化基本呈线性相关关系。

明确在役RC框架结构抗震能力退化的起始时间对其时变抗震能力评估具有重要意义。定义结构近倒塌破坏状态的震能力退化5%所对应的时间为其抗震能力退化的起始时间，在此基础上，通过式(21)计算得到6～8.5度设防水平下在役RC框架结构抗震能力退化起始时间分别为：33.00、34.15、35.53、37.20和41.94 a。该结果表明，随着设防水平降低，在役RC框架结构抗震能力退化的起始时间不断提前。考虑到中国多数沿海城市处于6度～7度的低设防烈度区，因此，评估该类地区服役超过35 a的在役RC框架结构的抗震性能时，应合理考虑服役龄期的影响。

4 结论

首先介绍了近海在役RC框架结构的数值建模方法，进而基于能力谱方法，提出了以可抵御地震动峰值加速度PGA为指标的在役RC框架结构抗震能力量化方法，并据此对不同设防水在役RC框架结构抗震能力劣化规律进行了系统研究，得出主要结论如下。

(1)基于能力谱方法提出的在役RC框架结构抗震能力量化方法，能够有效量化在役RC框架结构不同破坏极限状态可抵御的地震动峰值加速度PGA，从而直观反映在役RC框架结构的实际抗震能力。

(2)随着服役龄期的增长，近海在役RC框架结构轻微、中等、严重、近倒塌破坏极限状态的抗震能力近似呈线性关系退化，但由于不同设防水平下结构内部钢筋截面面积削弱程度不同，其退化速率随着设防水平的降低不断提高。

(3)相对轻微和中等破坏极限状态，服役龄期的增长对在役RC框架结构严重和近倒塌破坏状态的抗震能力影响更为显著。

(4)随着设防水平的降低，近海在役RC框架结构抗震能力退化的起始时间不断降低。

(5)综合考虑设防水平和服役龄期变化的影响，建立了近海在役RC框架结构不同破坏极限状态的时变抗震能力量化模型，其可近似表征近海在役RC框架结构的抗震能力劣化规律，但尚需实例验证。