某型导弹伸缩翼展开可靠性评估

朱星宏，李伟男，耿小亮，黄益民

（1.西北工业大学 力学与土木建筑学院，西安710129）

（2.中国空空导弹研究院 总体所，洛阳471009）

（3.中国空空导弹研究院航空制导武器航空科技重点实验室，洛阳471009）

0 引言

随着现代战争的发展，导弹开始呈现远程化、高精度、小型化的发展趋势。由于战机的弹仓有限，导弹的小型化能使战机携带更多的弹药。有时战机多携带一发导弹，在作战中就可以起着至关重要的作用。现在许多小型导弹都已采用折叠翼，与固定翼相比，折叠翼带来体积上的优势，但也伴随着展开时的可靠性问题。

在20世纪40年代，工程设计人员已意识到，产品的设计与安全分析中需考虑不确定因素带来的可靠性问题。经过几十年的发展，可靠性模型已经衍生出随机模型、模糊模型、凸集模型以及结合这三者的混合模型［1］。在此期间，吕震宙等［2-3］对可靠性模型进行了深入研究；除此之外，众多研究人员结合其他理论，例如宋明顺等［4］基于小样本失效数据对机械可靠性进行评估；范松［5］基于证据理论对机械可靠性进行优化设计方法研究；李志强等［6］提出的一种基于动态贝叶斯网络的某控制单元可靠性分析。随着Javelin标枪反坦克导弹的出现，早在20世纪90年代初，国内就有折叠翼展开时间、动载荷等相关研究［7-8］。之后M.P.Snyder等［9］利用Nantran分析了结构刚度以及展开角度的折叠机构动力学响应；P.J.Attar等［10］深入研究了折叠翼机构的非线性空气动力学行为；张玲等［11］提出了一种基于形状记忆合金的折叠弹翼展开机构的驱动方式；曾清香［12］设计了一种以扭簧为驱动动力源的飞行器折叠翼设计新方案，并进行详细的受力分析与实验；陈克等［13］从折叠舵的展开过程气动载荷设计、折展锁紧机构设计和舵面结构设计三个方面总结了关键设计技术及相关研究现状；王明［14］通过Adams对一种小型旋转折叠翼进行动力学仿真。而折叠翼的可靠性研究开始于21世纪，倪健等［15］对导弹折叠翼展开机构进行可靠性定性分析；李迪凡等［16］对导弹尾翼弹簧贮存寿命进行评估；周光巍等［17］对空空导弹贮存寿命的可靠性进行了论述；胡明等［18］运用Adams/In⁃sight对折叠翼展开进行了可靠性仿真；赵志强等［19］对舵翼展开机构的可靠性分析与实验研究进行了综述。上述研究针对折叠翼的动力学响应、空气动力学行为、驱动方式、储存寿命可靠性和展开可靠性都进行了深入的研究。相比于折叠翼，伸缩翼不仅可以减小弹翼体积，还能大幅度改变弹翼的展弦比，使弹翼的气动性能与任务需要相匹配［20］。

目前伸缩翼方面的研究仍处于起步阶段，R.M.Ajaj等［21］研究了可伸缩、多段以及跨度变形机翼的气动弹性行为，并探究了跨度变形作为颤动抑制装置的可行性；郭建国等［22］对非对称伸缩翼飞行器动力学建模及特性分析进行了研究；王江华等［23］对伸缩弹翼巡航导弹气动外形进行了优化。针对伸缩翼可靠性相关研究并不多见。

本文以某型导弹伸缩翼展开机构为研究对象，通过理论分析探索外来异物对伸缩翼定位失效的影响。采用Adams建立伸缩翼的参数化动力学仿真模型，结合Adams/Insight模块对机构的卡滞失效进行分析，探索固定销直径以及弹簧预载荷大小与配比对某型空空导弹伸缩翼的可靠性和定位杆冲击载荷大小影响。

1 伸缩翼展开机构组成及工作原理

某型伸缩翼展开机构较为复杂，其主要由翼面、展开机构、定位机构和锁定机构四部分组成，装配图示意图如图1所示。

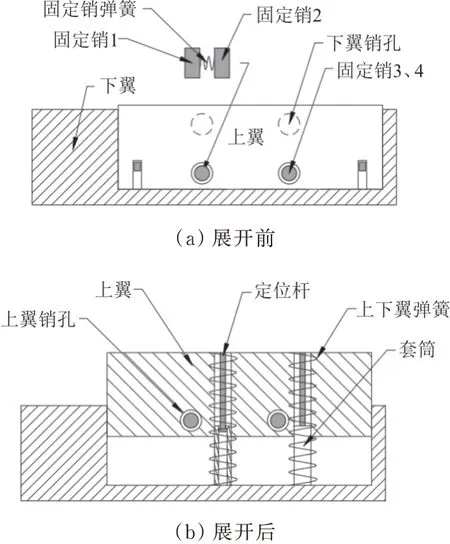
图1 伸缩翼整体构成Fig.1 The overall structure of the telescopic wing

套筒和定位杆使得上翼沿着正确的方向展开，以免在展开的过程中在下翼内产生卡滞，同时套筒内有阻挡结构防止上翼展开过位。固定销用于上翼到位时的固定，固定销弹簧是固定销插入销孔时的动力源。

展开前，上翼收缩在下翼内，在接收到展开信号后，上翼以上下翼弹簧为动力源立即弹出。当上翼到达指定位置后，固定销从上翼销孔插入下翼销孔内，完成上翼的固定。

2 伸缩翼的故障树分析

机构可靠度是指在规定的寿命要求与工作环境下，机构能完成规定功能，或不出现一、二等事故的概率［24］。

伸缩翼作为一种复杂机构，较以往的固定翼，将有更多原因导致失效，主要的失效模式为卡滞失效与定位失效，两种失效模式相互关联，原因和结果部分重合，只是侧重点不同。伸缩翼展开失效的故障树如图2所示，伸缩翼展开失效的故障树的基本事件如表1所示，失效模式与失效判据如表2所示。

图2 伸缩翼展开失效的故障树Fig.2 Fault tree of telescopic wing deployment failure

表1 伸缩翼展开失效的故障树基本事件［25］Table 1 Basic event of fault tree for telescopic wing deployment failure［25］

表2 失效模式与失效判据Table 2 Failure mode and failure criterion

经计算弹翼展开失效的故障树最小割集为：X1、X2、X3、X4、X5·X6·X7、X8、X9、X10、X11、X12。从 最小割集可以了解到，造成弹翼展开失效的原因大部分相互独立，这也反映出在设计这种展开机构时应该对每个环节加强冗余设计，降低每个环节的故障率，才能提高整体可靠性。由于篇幅有限，本文主要从加工和制造误差方面进行弹翼可靠性分析，暂未考虑气动载荷影响。定位杆与套筒长度不匹配和固定销与上下翼的孔径不匹配主要受到加工和制造误差的影响，而套筒内进异物也是不可忽视的因素［25］，因此本文将从这三个方面进行弹翼的可靠性分析。

3 伸缩翼展开机构的可靠性分析

机构失效大体分为定位失效和卡滞失效，两种失效方式既有区别又有一定联系。定位失效主要指机构无法准确按照指令要求运动或停止；卡滞失效是机构的驱动力或力矩不能克服阻力，导致机构运动过慢或无法运动［24］。

3.1 定位失效

在实际生产过程中，伸缩翼在生产装配完成后需进行展开测试，理论上伸缩翼不存在由于零件尺寸问题导致的展开失效问题。但现实中如果由于保存不当导致套筒内进入异物或者高空中套筒内壁结冰就可能导致在展开时上翼不能到达正确位置，从而固定销插入时阻力过大或者无法插入，这种情况一般用定位可靠性来表示。其安全边界方程如式（1）所示［24］。

式中：δ为实际位移，可取正态分布；δ*为容许位移，可取定值或随机分布。

从加工尺寸制造误差出发，定位杆长度、套筒长度、固定销直径的变化和可能由于生产、存储和使用中产生的如碎屑、冰粒等杂质将共同作用，成为影响固定销插入的主要因素，因此以这些因素作为变量，来考虑伸缩翼展开失效问题。由于伸缩翼内部固定销与销孔的配合不同于以往机械装配中的手动装配，它是展开后自动配合的，还有时间要求，因此在传统的销孔配合中并没有与之对应的参考。本文以《互换性与测量技术》［26］作为参考，在需要松弛可动配合情况下选定Φ14c7/H7这一公差。异物大小以导杆和套筒的间隙作为参考，其最大直径不超过导杆与套筒孔直径的差值0.1 mm，其余变量的大小及其分布如表3所示。

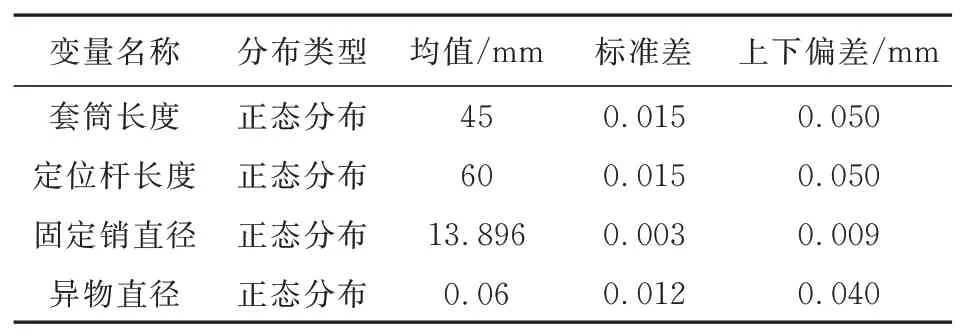
表3 各变量及其分布Table 3 Distribution of variables

固定销容许位移示意图如图3所示，上下翼的销孔直径为14 mm。在固定销能刚好插入上翼销孔的情况下，设下翼销孔轴线所在y方向坐标为0，则上翼销孔轴线所在的y方向坐标为

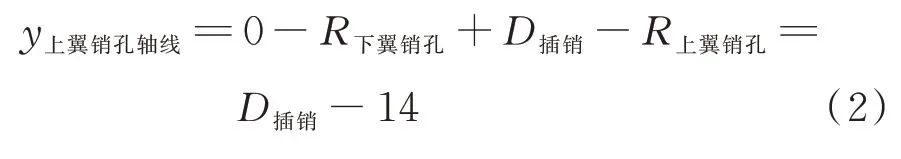
式中：R上翼销孔和R下翼销孔分别为上下翼销孔的半径；R插销为固定销的半径。

因此上翼销孔轴线容许位移δ*为

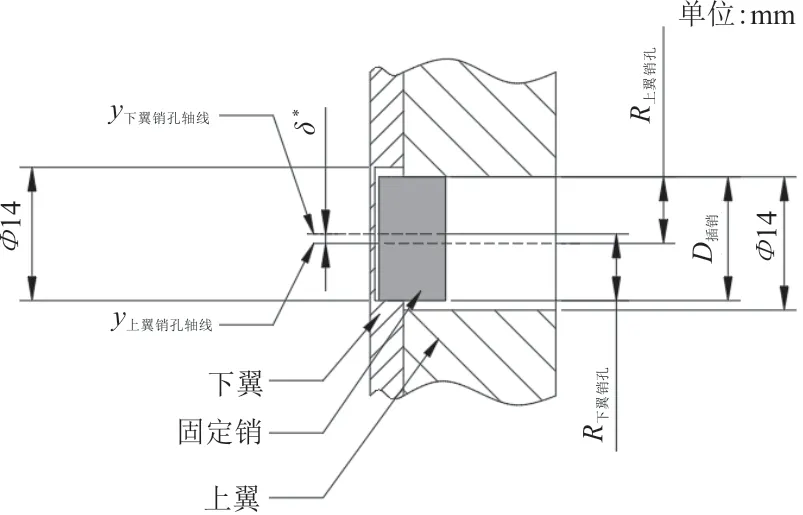
图3 固定销容许位移示意图Fig.3 Schematic diagram of allowable displacement of the bolt

根据参数化分析可知固定销直径分布服从D插销～N(6.5，0.12)，由正态分布的特性得到：

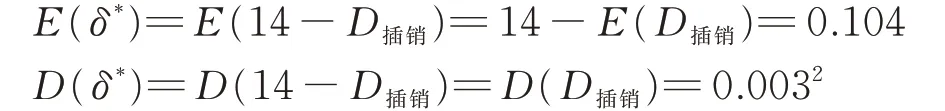
因此上翼销孔轴线容许位移分布服从δ*～N(0.104，0.0032)。

定位杆、套筒连接示意图如图4所示，其中定位杆和上翼固定在一起，套筒和下翼固定在一起。

图4 定位杆、套筒连接示意图Fig.4 Schematic diagram of the connection between the positioning rod and the sleeve

当定位杆和套筒长度为原始长度60、45 mm时，则展开后则上下翼销孔会完全重合在一起，如图5所示。

图5 伸缩翼展开前后剖视图Fig.5 Sectional view of the telescopic wing before and after deployment

若定位杆和套筒产生Δ1和Δ2的偏差并混入一个直径为Δ3的异物，则在伸缩翼展开后，上翼销孔轴线会产生δ=Δ1+Δ2-Δ3的位移，如图6所示。

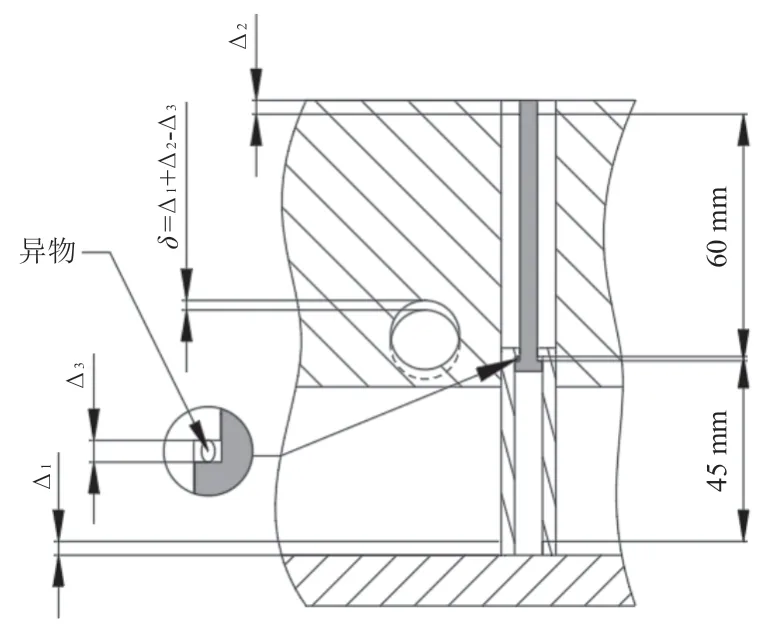
图6 上翼销孔轴线位移δ示意图Fig.6 Schematic diagram of displacementδof the pin axis of the upper wing

根据正态分布的特性，同理得到：

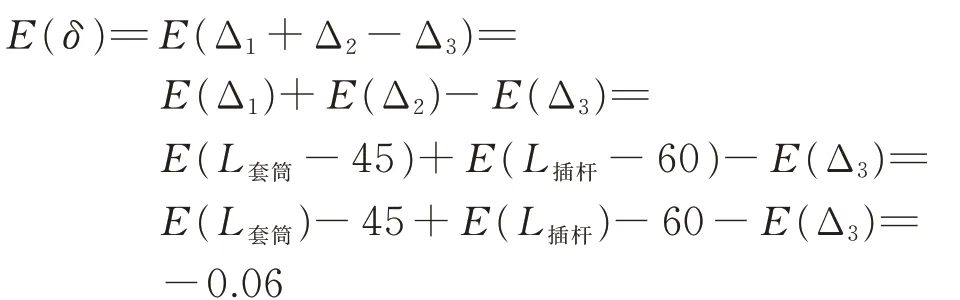
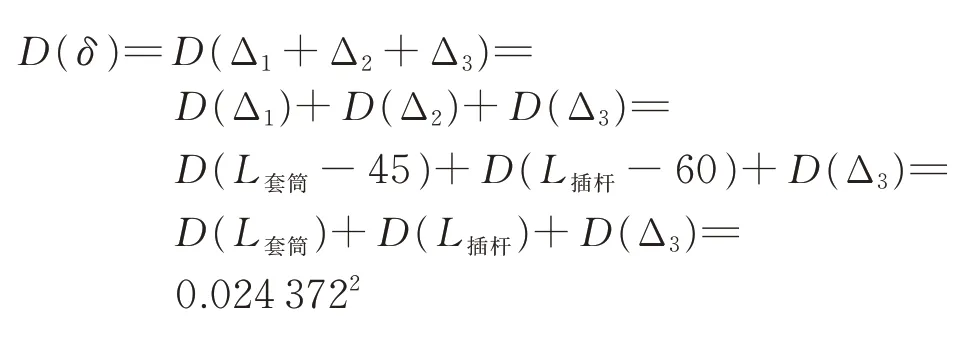
上翼销孔轴线的实际位移分布服从δ～N(-0.06，0.024 3722)。

由于固定销只需插入下翼销孔内，则单个固定销的实际安全边界方程如式（4）所示。

同时必须确保所有固定销插入，因此伸缩翼展开机构的实际安全边界方程如式（5）所示，当所有的固定销容许位移大于实际位移时伸缩翼才展开成功。

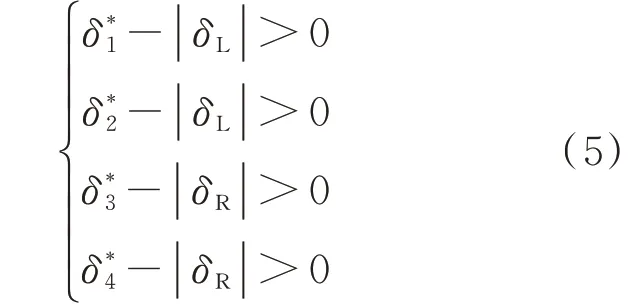
从δ*和δ服从正态分布可知，δ*-|δ|并不符合常见的分布，因此运用蒙特卡洛法［27］进行失效概率求解。设计中的伸缩翼，无法确定套筒内出现异物的概率，因此分别就有异物和无异物的情况进行1 000万次抽样计算，可靠性结果如表4所示，有无异物的δ*-|δ|分布如图7～图8所示。

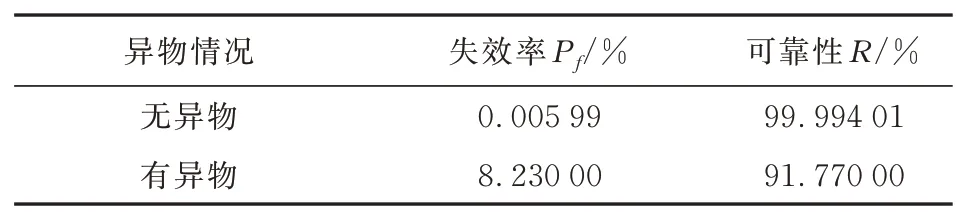
表4 有无异物时的伸缩翼展开机构可靠性Table 4 Reliability of the telescopic wing deployment mechanism with or without foreign objects

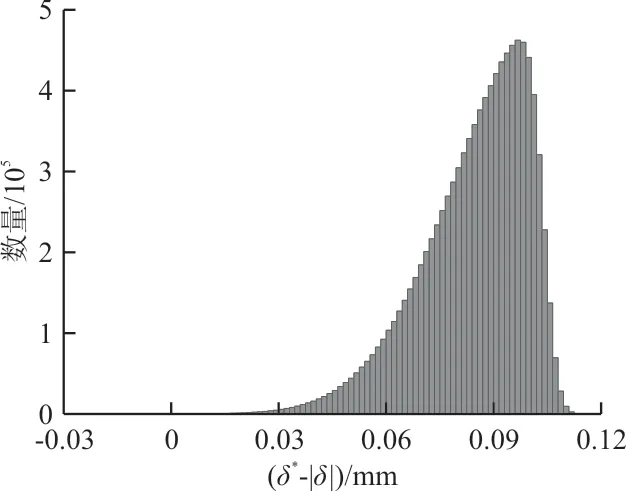
图7 无异物时δ*-|δ|的分布Fig.7 Distribution ofδ*-|δ|without foreign body

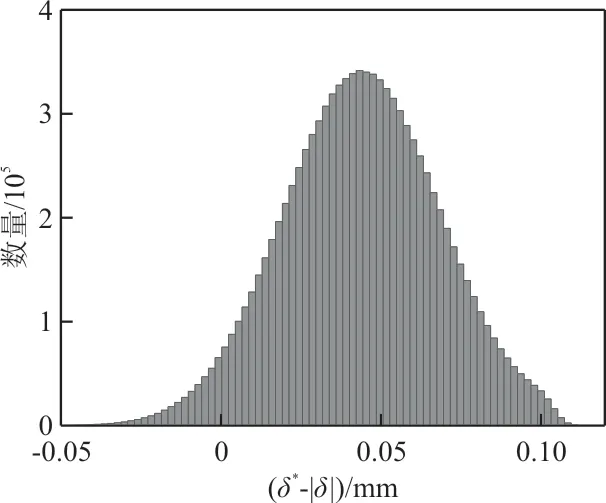
图8 有异物时δ*-|δ|的分布Fig.8 Distribution ofδ*-|δ|with foreign objects

由于四个固定销的δ*-|δ|分布相同，因此图7～图8中只列出了1号固定销的δ*-|δ|分布。在Matlab中运用卡方检验对有异物时的δ*-|δ|分布进行拟合优度检验，在显著性水平α=0.01的条件下，p值为0，不属于正态分布。

在无异物进入套筒内的情况下伸缩翼展开这一过程的可靠性非常高，当有异物进入时可靠性会明显下降。因此在定位失效这一方面的失效概率主要取决于异物的大小和出现概率。

3.2 卡滞失效

不同于定位失效主要关注零件几何尺寸与加工公差造成的可靠性问题，卡滞失效还将零件之间的摩擦这一因素纳入考虑范围。但对于伸缩翼这种精密结构而言，要构建零件尺寸与展开时间的理论关系十分困难，若采用Adams这一多体动力学软件则可以很好模拟这一过程。

此弹翼的设计目标为0.1 s内完成展开，允许误差为3%［19］，在插入前四个固定销与下翼销孔底部的距离为3 mm，如图9所示。

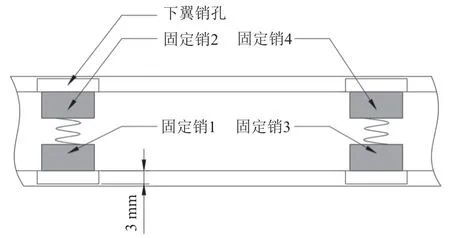
图9 固定销1～4位置示意图Fig.9 Schematic diagram of the positions of the fixing pins 1～4

上翼展开到位，固定插入销孔，固定销插入速度曲线如图10所示，可以看出：由于刚插入时固定销与销孔配合并不良好，固定销在距离销孔底部距离2 mm处与销孔内壁发生碰撞，速度锐减；待固定销重新调整位置与销孔配合良好，固定销在弹簧作用下重新加速，并且在插入2 mm时速度达到了475 mm/s，剩余1 mm路程可以在1/475≈0.002 1 s内完成，完全在3%允许范围内。因此假定在0.1 s时固定销与下翼销孔底部距离小于1 mm则判定伸缩翼展开成功。

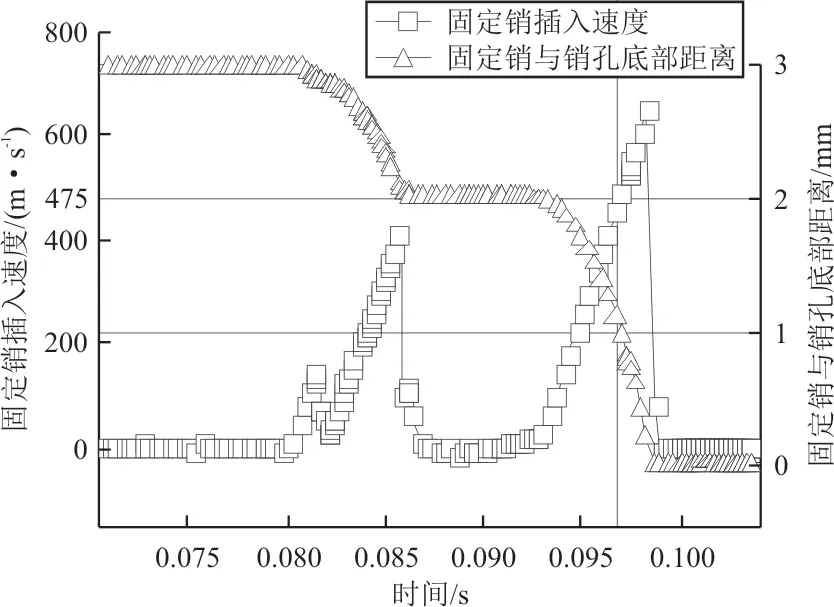
图10 固定销插入速度曲线Fig.10 Insertion speed curve of fixed pin

零件尺寸分布依然使用表3参数，固定销与下翼使用基于碰撞函数的接触算法，接触刚度和阻尼使用默认参数，分别为105N/mm和10 N·s/mm，动摩擦系数为0.1，静摩擦系数为0.3。固定销弹簧的预载荷为0.6 N，刚度为0.032 N/mm。不考虑有异物的情况，在Adams中进行300次仿真，对结果统计发现离销孔底部距离小于1 mm的算例为0次，即使将伸缩翼伸出时间上限延长5%，成功算例有33次，当伸出时间上限延长20%，有289次成功算例，很明显这不符合设计要求。为解决这一问题，将固定销直径均值减小至13.82 mm，依然是IT7级的加工精度，伸缩翼伸出时间上限仍然保持0.1 s，其他参数不变。在Adams中进行300次仿真，仿真结果为：在0.1 s内12次伸出并锁定成功，但统计发现其中有291次是固定销1、2已经完全插入，而固定销3、4只有12次完全插入。其中某一次的情况如图11所示，可以看出：当上翼达到指定位置时，固定销1～4会同时插入，并且随着时间的推移固定销3、4的插入速度明显变慢，并且在这段时间内固定销3、4的质心依然在摆动，如图12所示。

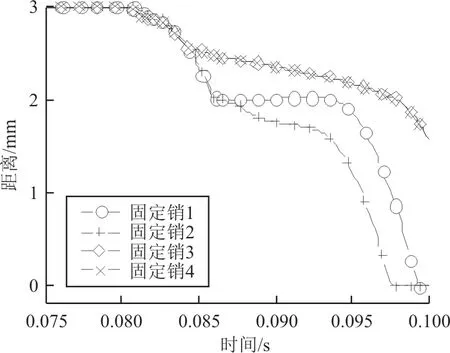
图11 固定销与下翼销孔底部距离Fig.11 Distance between the fixing pin and the bottom of lower pin hole

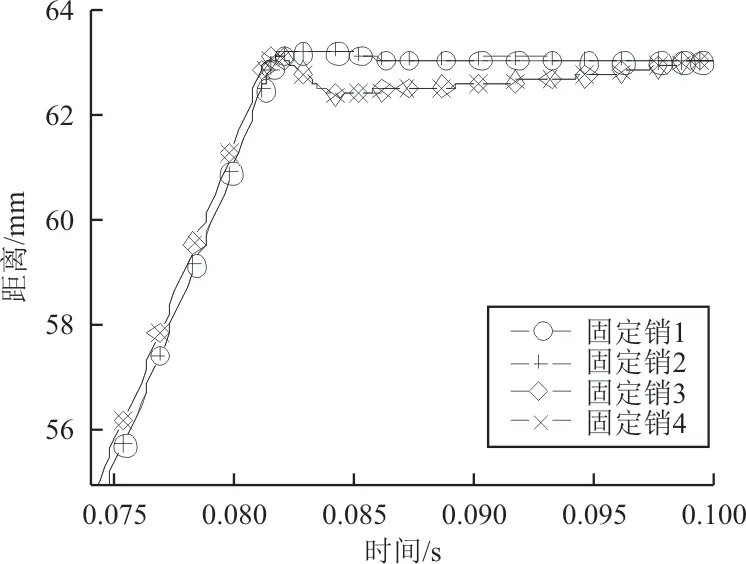
图12 固定销的质心延展开方向的距离Fig.12 Coordinates of the center of mass extension of the pin

3.3 伸缩翼卡滞失效原因分析

导致卡滞失效的原因可能是左右两根上下翼弹簧力大小相等时，弹簧力在质心处的合力矩不为零导致的细微差别，如图13所示。

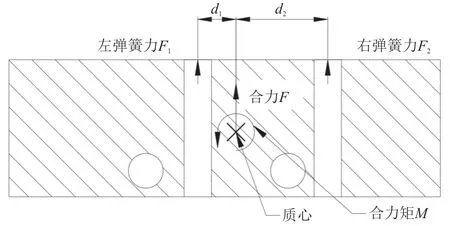
图13 上翼质心位置与上下翼弹簧合力作用点Fig.13 The position of the center of mass of the upper wing and the combined action point of the upper and lower wing springs

为探索这种细微差别对展开时间的影响，本文针对不同方案下的伸缩翼展开机构可靠性（如表5所示）做了以下三种尝试，并进行300次仿真。

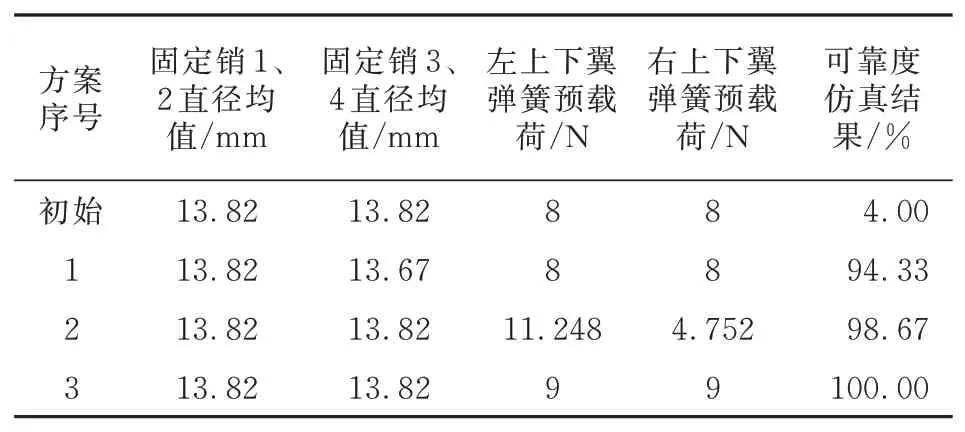
表5 不同方案下的伸缩翼展开机构可靠性Table 5 Reliability of telescopic wing deployment mecha⁃nism under different schemes

1号方案：将固定销3、4的直径均值减小到13.67 mm，其他参数不变时，这时固定销3、4的质心摆动并不能影响其插入。1号方案的可靠度大幅提高，但这也带来另一个问题就是销孔间隙过大。

2号方案：调整弹簧预载荷的配比，将左右的上下翼弹簧各8 N调整为左上下翼弹簧11.248 N，右上下翼弹簧4.752 N，从而使得弹簧力在质心处合力矩为零，上翼可以平稳展开。以表5中方案2的均值进行仿真，其仿真结果如图14所示。

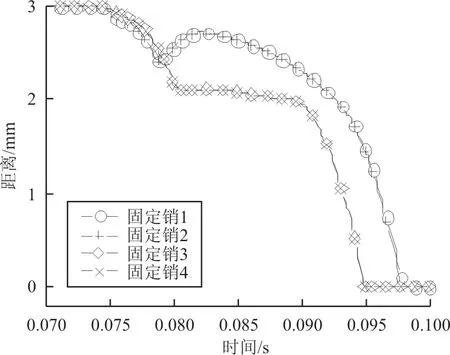
图14 2号方案下固定销与下翼销孔底部距离Fig.14 Distance between the fixing pin and the bottom of lower pin hole under schemes No.2

在这种工况下固定销3、4反而比固定销1、2展开顺利，再考虑到左右定位杆与套筒在长度上的微小差别，因此四个固定销同时插入的概率非常低。但由于弹簧和力作用在上翼质心时，上下翼间只需用一个很小的接触力就能维持上翼的平衡，从而减小上下翼间的摩擦力，使得上翼能够更快地弹出，完成整个伸缩翼在0.1 s内展开的目标。

3号方案：提升上下翼弹簧的预载荷，这无疑可以缩短展开时间，为固定销的插入留出更充分的时间，但采用这种方法时可能导致展开时定位杆与套筒的接触力过大。以表5中的参数进行仿真，结果如图15～图16所示。

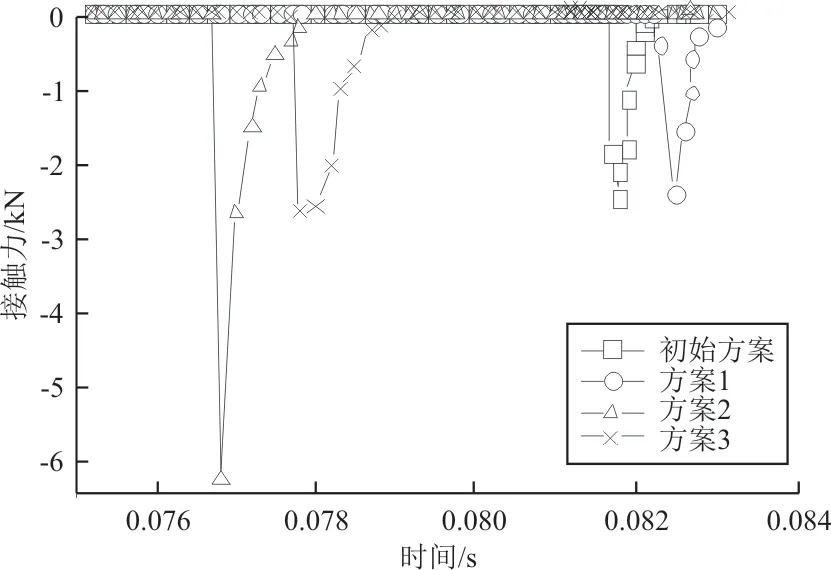
图15 左侧套筒与定位杆接触时的冲击力Fig.15 Impact force when the sleeve contacts the guide rod on the left

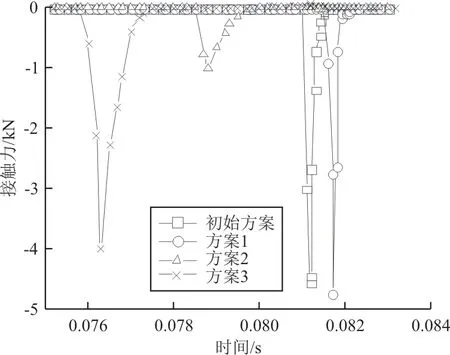
图16 右侧套筒与定位杆接触时的冲击力Fig.16 Impact force when the sleeve contacts the guide rod on the right

通过对3种方案的接触力对比发现，稍微增大上下翼弹簧的预载荷并不会对套筒和定位杆的接触力有太大影响，反而2号方案下的接触力更大。可见适当增加上下翼弹簧的预载荷能够有效减少伸缩翼展开机构的卡滞失效，具体该采用哪种方法还是需要通过试验验证之后在各种方法间进行权衡。

4 结论

（1）本文通过理论计算得到在存在异物的工况下，伸缩翼展开机构的定位可靠性为91.77%，远低于无异物下工况的99.994 01%，因此为保证导弹伸缩翼的定位可靠性必须在将其零件加工精度提升到较高的精度，同时确保伸缩翼在一个良好的环境内储存以减小外来异物的影响，从而提高定位可靠性。

（2）在相同尺寸参数下，卡滞可靠性远低于定位可靠性，即使将固定销直径均值从13.896 mm降低至13.820 mm，卡滞可靠性仍只有4%。

（3）上下翼弹簧在上翼质心处产生的附加力矩是导致卡滞可靠性下降的主要原因。调整弹簧配比以减小附加力矩，增加弹簧的预载荷，减小固定销直径都可将伸缩翼展开机构的卡滞可靠性提升至94%以上，并且增加预载荷的效果更好。