缝翼尖端延伸对流场及噪声特性的影响
王红建,张巧,田峻源
(西北工业大学航空学院,西安710072)
0 引言
随着民航工业的迅速发展,民航客机的气动噪声正成为人们关注的主要问题之一。研究表明,在飞机起降阶段,相对于发动机噪声,机体噪声占比明显增加;机翼中的缝翼处于打开状态,且几乎在整个翼展方向部署,是机体噪声的主要来源[1]。
实验及数值仿真研究表明,缝翼噪声频谱分为宽带、低频窄带和高频窄带噪声[2]。各频段噪声的产生与缝翼流动结构特性密切相关,例如,缝翼尾缘流场中有规律的涡脱落引发高频窄带噪声;缝翼凹腔流动中涡与尾缘壁面撞击产生中低频宽带噪声[3];缝翼尖端、凹腔与尾缘之间剪切层的生成、发展和反馈与开放式凹腔相似[4],主要形成低频窄带噪声。涡脱落引发的高频窄带噪声在实际飞行试验中并不明显[4-5],因此研究人员主要关注中低频段的缝翼噪声抑制问题。
对流场主动干预进行噪声抑制的方法主要是在缝翼尖端或其尾缘附近进行吹吸气[6-7]。该方法可改变涡流的原有性态,降低其湍动能强度,进而抑制噪声辐射,但需外部能量的注入。缝道封闭[8]可消除缝翼凹腔的复杂流动,彻底消除该区域的噪声源,但因其对翼型升力的严重损伤而无法使用。缝翼凹腔填充[9]使缝翼尖端到尾缘的几何外形光滑连续,消除了缝翼剪切层,可较大幅度地降低中低频段的缝翼噪声;王红建等[10-12]针对缝翼与主翼的相对几何位置,结合缝翼自适应尾缘变形技术,研究了缝翼位置参数与尾缘变形对缝翼远场噪声辐射特性的影响,发现缝翼适当的位置调整和结构变形均可有效降低远场噪声辐射。
为了避免对缝翼外形进行较大幅度的改变,研究人员开始采用缝翼小变形技术,通过调整缝翼剪切层的生成、发展及其流场涡结构的运动等来抑制噪声辐射。F.R.Do Amaral等[13]发现凹腔凸起可阻止回流区沿缝翼凹腔表面的流动,且其位置与降噪效果相关性很高,特定位置凸起可明显降低回流区湍动能;L.Botero等[14]利用LBM和FW-H方法分析了尖端角度、延伸长度及尾缘角度对缝翼流场与气动噪声的影响,发现延伸长度、尾缘角度与缝翼噪声的相关性较高,较长的延伸会增大窄带和宽带噪声,而尖端角度对缝翼噪声的影响不大;Zhang Y等[15]通过实验研究发现,缝翼尖端延伸可延迟气流分离,缩短剪切层发展距离,削弱剪切层的不稳定性,可在一定程度上降低窄带噪声;M.Khorrami等[16]对波音777高升力装置进行二维仿真,发现尖端延伸改变了剪切层特性,其涡结构的运动被限制在较窄的范围内,在附着点更靠近缝翼尾缘位置,涡结构强度与噪声辐射显著降低,且延伸长度增加使剪切层涡结构变弱,较长的延伸可改变缝翼尾缘流动的不稳定性,使高频窄带噪声明显降低,其研究结论与L.Botero等[14]有一定分歧。
缝翼尖端延伸对缝翼流场和噪声辐射具有重要影响,但目前利用该技术进行降噪的相关研究还很不充分。一是尖端延伸长度与降噪效果正相关的结论存在争议;二是延伸方式对缝翼流场与噪声影响的内在机理还不清楚。为了进一步探究缝翼尖端延伸方式对缝翼流场与噪声辐射特性的影响,本文提出缝翼尖端沿剪切层方向和壁面切向两种延伸形式,研究这两种延伸方式的流场与噪声辐射特性,并结合瞬态流场结构分析方法和窄带噪声预测模型,探索缝翼尖端延伸对其流场和噪声的作用机理。
1 数值研究方法
1.1 基于SST湍流模型的DDES非定常流场分析
DES方法结合了LES和RANS的优势,综合考虑了计算精度和效率[17]。而DDES[18]方法避免了DES算法中因边界层内网格过密导致的网格诱导分离。这些方法早期基于SA湍流模型,后来逐步应用到其他湍流模型中,如A.Travin等[19]基于SST湍流模型提出的DDES方法。SST湍流模型在边界层及分离流动模拟中效果更好,因此,本文选择基于SST湍流模型的DDES方法进行非定常流场分析。
DDES方法中的长度尺度定义为
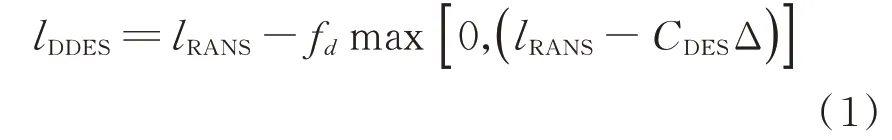
式 中:CDESΔ为LES的 长 度 尺 度lLES;fd为 屏 蔽函数。
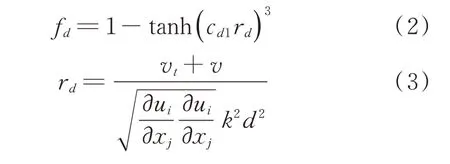
式中:k为卡曼常数;d为点到壁面的距离;v、vt分别为分子、湍流黏性系数。
参考文献[20]中关于DDES-SST的结论,将式(2)中常量cd1设为20。rd为当地湍流尺度与其距壁面距离的比值,靠近壁面,rd较大,fd趋近0,计算切换为RANS,避免LES在边界层内部应用;远离壁面rd≪1,fd趋近1,则切换为LES方法。
式(1)中,lRANS为SST湍流长度尺度:CDES的函数表达式为
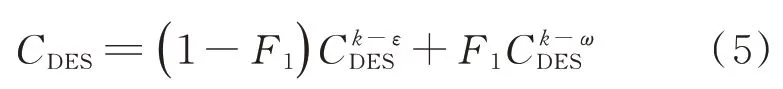

式中:F1为SST模型中的弯曲函数系数,见参考文献[20]的值分别设为0.61和0.78。亚格子网格尺度Δ为最大当地网格间距:

1.2 基于FW-H积分方程的远场噪声分析
远场噪声计算采用FW-H(Ffowcs Wiliams-Hawking)积分方程[21]:

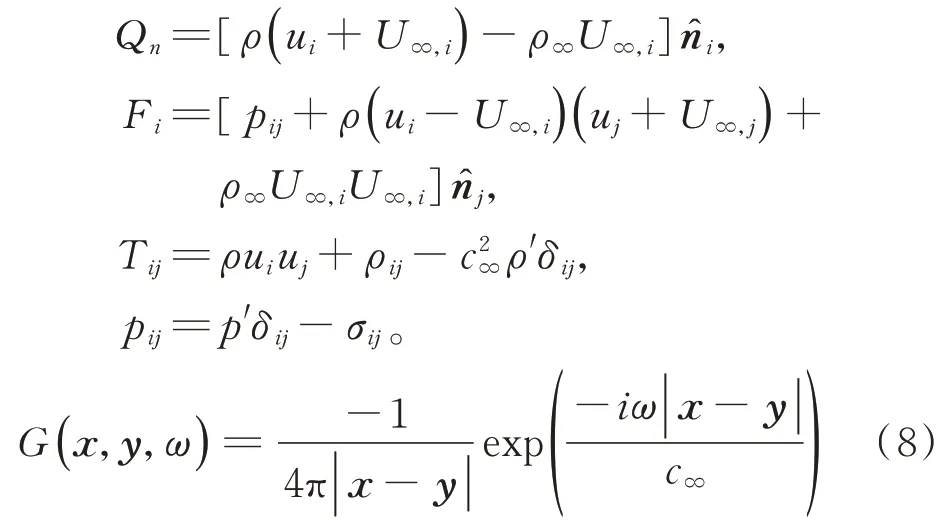
其中,式中:p′为所求声压;x为观察者位置矢量;y为声源位置矢量;ω为角频率;ρ和ρ∞分别为当地和自由来流密度;c∞为自由来流声速;ui和U∞,i分别为当地和自由来流速度;σij为黏性应力张量;nˆj为表面S外法向向量;G为自由空间格林函数。
考虑到飞机起降阶段马赫数较低,四极子声源很弱,可以忽略;同时,本文主要关注缝翼远场噪声,不考虑缝翼与主翼之间的声波反射效应。有研究显示,缝翼的固壁积分面与可穿透积分面对远场噪声的仿真结果近似[22],故本文采用缝翼壁面作为积分面。
2 仿真模型与数值方法验证
2.1 仿真模型及流场基本参数
采用30P30N多段翼型作为基准构型(如图1所示),缝翼及襟翼的偏转角均为30°,缝翼弦长Cs=0.15C(C为多段翼收紧弦长0.457 m),襟翼弦长Cf=0.3C,缝翼尾缘为钝体,其厚度为4.5×10-4C。缝翼与襟翼的缝道宽度(Gap)分别为2.95%C、1.27%C,缝翼与襟翼的重叠量(Over⁃lap)分别为-2.5%C、0.25%C;其自由来流条件与试验条件一致,马赫数M∞=0.17,基于翼型弦长的雷诺数为ReC=1.7×106,攻角为8°。

图1 30P30N翼型结构Fig.1 Airfoil structure 30P30N
2.2 计算网格与数值方法
三维多段翼网格(如图2所示)节点总数约1×107,第一层网格与壁面的距离为2×10-5C,其黏性无量纲尺度满足y+≈1,符合SST对边界层网格的要求。远场边界位于翼型收紧前缘点50倍弦长处,展向尺度设为0.061 5C,网格节点数为31,展向边界条件设置为周期性边界条件。D.P.Lock⁃ard等[23]对翼型展向相关性进行研究,发现展向长度大于0.04C时,相关性趋近于0。因此本文选取的展向范围足以显示缝翼周围三维流场的流动变化情况,计算域满足缝翼流场的非定常模拟计算。
本文采用基于SST湍流模型的DDES瞬态流场模拟方法。首先,利用RANS求解得到稳态流场;其次,以稳态流场结果作为DDES瞬态计算的初始条件,先进行时间推进迭代时长约6C/U∞,以消除定常状态;随后开始记录数据,继续推进迭代时长约10C/U∞,得到最终的瞬态流场数据。空间和时间离散精度均为二阶,非定常计算时间步长Δt=5×10-6s;最后,将固壁面的流场数据用于FW-H积分方程,获得远场监测点的声压级分布。

图2 模型的CFD计算网格Fig.2 The model’s CFD computing grid
2.3 数值方法验证
基于上述分析方法,对30P30N基准构型进行仿真模拟,对比所得翼型表面压力分布与JAXA实验结果[24](如图3(a)所示),可以看出:翼型表面压力系数分布与实验结果基本吻合。为进一步验证在其他攻角下的准确性,使用5.5°攻角的压力分布与JAXA[24]和FSU[2](Florida State University)的风洞实验值进行对比(如图3(b)所示),可以看出:结果也十分吻合,可充分验证仿真方法的可行性与准确性。

图3 压力系数对比Fig.3 Comparison of surface pressure coefficients
对比瞬态展向涡量(如图4所示),可以看出:本文仿真结果与K.A.Pascioni等[25]的PIV实验结果基本一致,可清晰捕捉到剪切层发展轨迹与凹腔区域涡结构的运动状态,吻合较好。

图4 PIV[25]与CFD计算值瞬态展向涡ωzC/U∞对比Fig.4 Comparison of transient transversal vortex ωzC/U∞between PIV[25]and CFD
以收紧翼型前缘点为圆心,10倍翼型弦长为半径,290°方向处设观测点对比缝翼噪声频谱,如图5所示,可以看出:本文5.5°攻角下的噪声频谱与BANC III[26]所得的结果基本一致;在8°攻角时,本文的噪声频谱窄带峰值较低,频率左移,与文献[27]所得结论一致,验证了本文仿真计算结果的准确性。
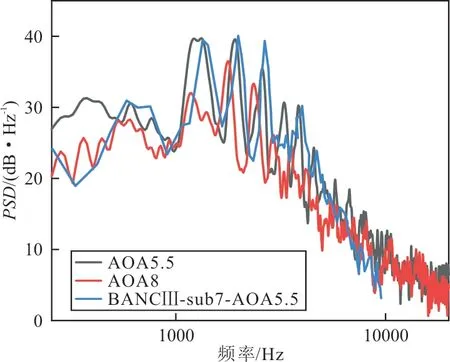
图5 声压频谱对比图Fig.5 Contrast diagrams of sound pressure spectra
3 缝翼尖端延伸对流场及气动噪声的影响
3.1 缝翼尖端延伸形式
基于30P30N基准构型,采用缝翼尖端沿外壁面切向和剪切层方向两种延伸方式(ext,sheerext)及延伸长度(1和2分别为0.15Cs、0.26Cs)进行研究,如图6所示。计算工况为:马赫数Ma=0.17,攻角α=8°,雷诺数Re=1.7×106。
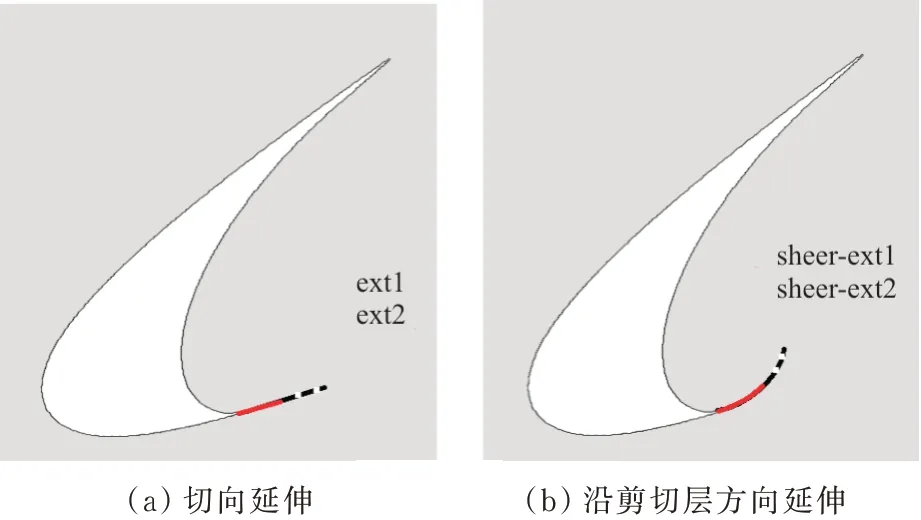
图6 缝翼尖端的两种延伸形式Fig.6 Two types of slat cusp extensions
3.2 流场特性
缝翼压力系数对比如图7所示,可以看出:切向延伸(图7(a))使缝翼前缘内壁面压力系数降低,尤其是延伸量增加的情况;而沿剪切层方向延伸(图7(b)),缝翼吸力面压力系数略有升高,其余部分与基准结构基本保持一致;尖端延伸(图7(c))对机翼构型的整体压力系数分布基本没有影响。


图7 缝翼压力系数对比(baseline为基准结构)Fig.7 Comparison of slat pressure coefficients
基准结构(如图8(a)所示)中,剪切层形成初始阶段,湍动能相对较低。随着流向距离增加,三维结构占据主导,剪切层上呈现较高的湍动能,直至与缝翼尾缘壁面撞击;撞击后再附着区域湍动能激增,导致缝翼尾缘处出现湍动能峰值。
切向延伸(如图8(b)和图8(c)所示)的导向作用使剪切层特征距离增加,回流区面积显著增大。尖端下游区域的低湍动能值区域明显减小,而回流区高湍动能值略有降低。沿剪切层方向延伸(如图8(d)和图8(e)所示),再附着区仍有湍动能集中,但降幅明显。凹腔下游区域的湍动能(TKE)值大幅下降,表明剪切层发展至尾缘区域引起的空气脉动更小,产生的噪声辐射更低,且延伸量增加特性更加明显。
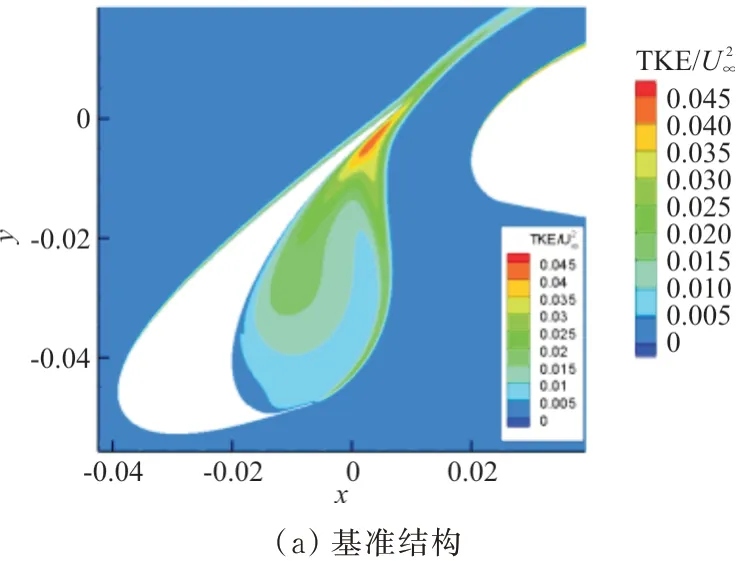

图8 湍动能TKE云图Fig.8 TKE diagram
对比不同延伸形式的瞬态展向涡量,如图9所示,可以看出:基准结构(图9(a))中高涡量值主要集中在剪切层附近。气流分离后,Kelvin-Helm⁃holtz的不稳定性使气流迅速卷起向尾缘运动,与外部气流耦合作用使剪切层与其周围区域压力梯度不断增大,气流有旋情况持续加剧,直至与缝翼尾缘壁面撞击;部分分离涡卷入回流区,于缝翼内壁面形成二次分离涡,导致此区域涡量值高于其他区域。
相比于基准结构,切向延伸(图9(b))使剪切层运动轨迹增加,大量离散涡卷入回流区,尤其是在延伸量增加的情况(图9(c))下;沿剪切层方向延伸(图9(d))的展向涡结构更加稳定,剪切层的长度和宽度均大幅减小,进入回流区的二次分离涡结构数量明显减少;且延伸量增加(图9(e)),缝翼凹腔区域中大尺度涡结构数量更少,能在接近尾缘区域仍保持良好的二维特性。
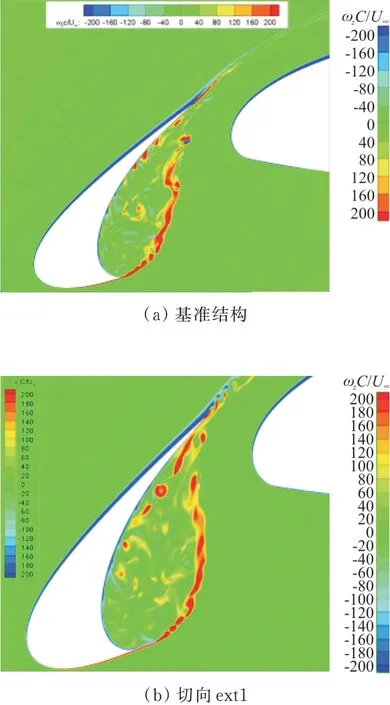
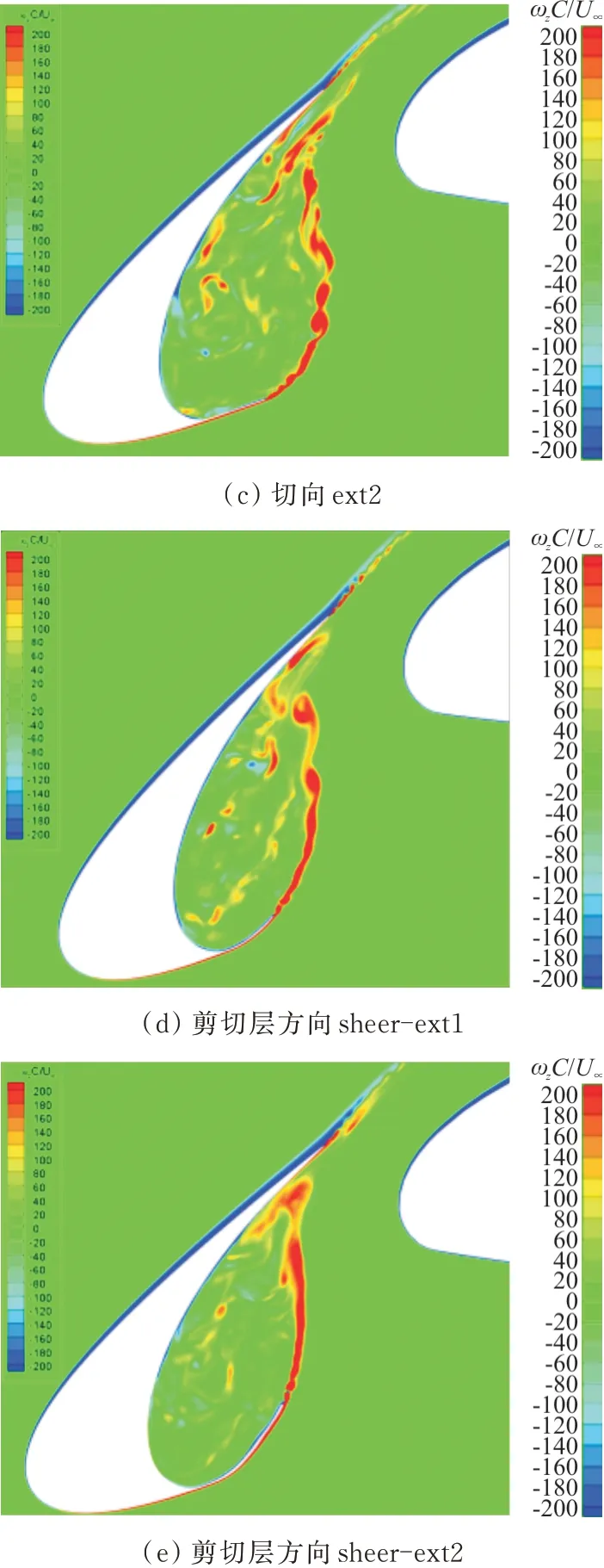
图9 瞬态展向涡量ωzC/U∞云图Fig.9 Transient transverse vorticityωzC/U∞diagram
为进一步呈现流场中瞬态涡结构的运动状态,以无量纲瞬态涡量ωzC/U∞为渲染深浅,对比Q准则等值面云图(如图10所示)。由于速度变化和Kelvin-Helmholtz不稳定性,基准结构中(图10(a))展向涡从靠近尖端处卷起,随着流向距离增加,准二维涡结构不断发展形成三维涡结构;其空间尺度不断变大,展向效应逐渐增强,单位能量尺度变大,直至与再附着区撞击。与基准结构相比,切向延伸(图10(b)和图10(c))只在尖端附近区域保持良好的展向涡特性;而沿剪切层方向延伸(图10(d)和图10(e))可在较长轨迹上保持较好的二维展向涡特性。

图10 Q准则瞬态展向涡量等值面云图Fig.10 Q criterion transient transversal vorticity contour map
3.3 气动噪声特性
为了探究缝翼尖端延伸对近场压力脉动的影响,在缝翼凹腔内设置压力监测点,如图11所示。沿剪切层方向延伸,在P1点(如图12(a)所示)处的噪声频谱基本没有发生改变,但其高频窄带峰值增加;延伸量增加,宽带噪声略有下降;在P2点(如图12(b)所示),延伸量增加,压力脉动频谱降低;沿剪切层方向延伸可降低缝翼凹腔内部的压力脉动水平。
相比于基准结构,沿剪切层方向延伸使P3点处(如图12(c)所示)压力脉动频谱降低,但在2.3 kHz有一处较高的窄带峰值;使P4点(如图12(d)所示)宽带噪声略有降低;延伸量增加,低频段压力脉动大幅降低;而切向延伸使P3、P4点处压力脉动水平增加。因此,沿剪切层方向延伸可有效改善缝翼尾缘碰撞区及其向后的压力脉动,削弱剪切层的不稳定性,进而降低了缝翼噪声。
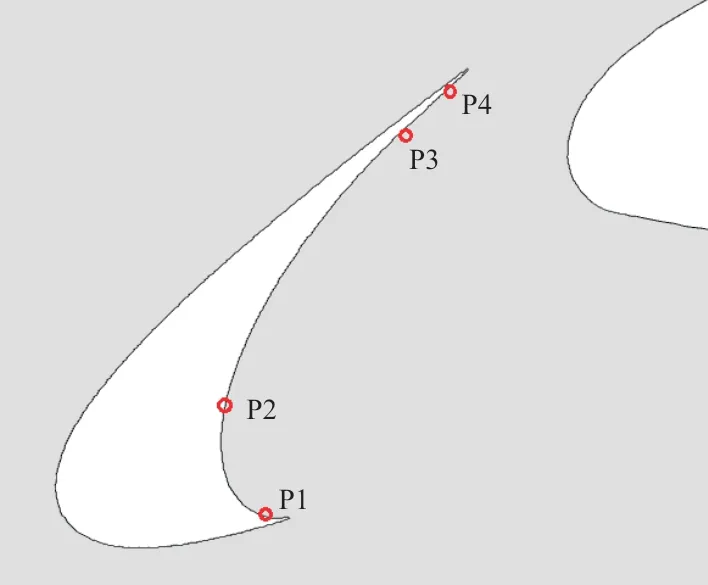
图11 缝翼凹腔内部压力脉动监测点示意图Fig.11 Schematic diagram of monitoring points for pressure fluctuation in slat cavity


图12 缝翼凹腔内部近场监测点压力脉动频谱图Fig.12 Spectra of pressure fluctuation at near-field monitoring points in slat cavity
对比远场指向性图(如图13所示),可以看出:缝翼尖端沿剪切层延伸(图13(a))的远场声压级在150°、270°和330°区域内明显减弱,但在其他方向上略有升高;而切向延伸则导致整体声压级上升(图13(b))。
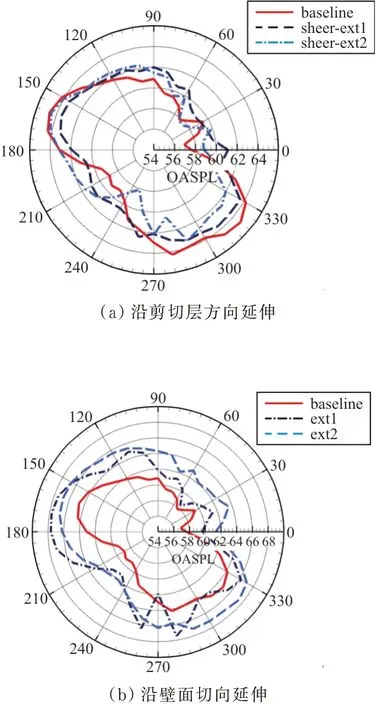
图13 远场噪声指向特性对比Fig.13 Directivity contrast of far-field noise
沿剪切层方向延伸(如图14(a)所示)可使宽带噪声在小于1 kHz范围内降低约3 dB,窄带峰值频率普遍右移;延伸量增加,在2.3 kHz有一个较大峰值,其余频段噪声频谱均有降低。切向延伸(如图14(b)所示)使1 kHz左右的宽带和窄带峰值减小;而延伸量增加,宽带噪声明显增加。
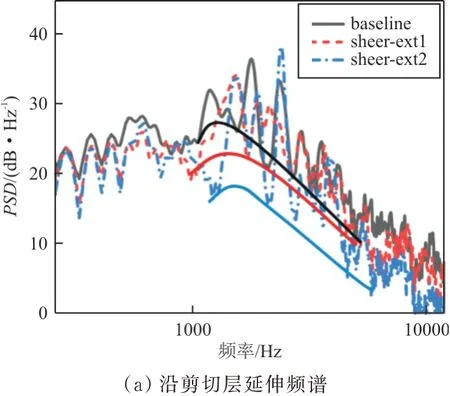
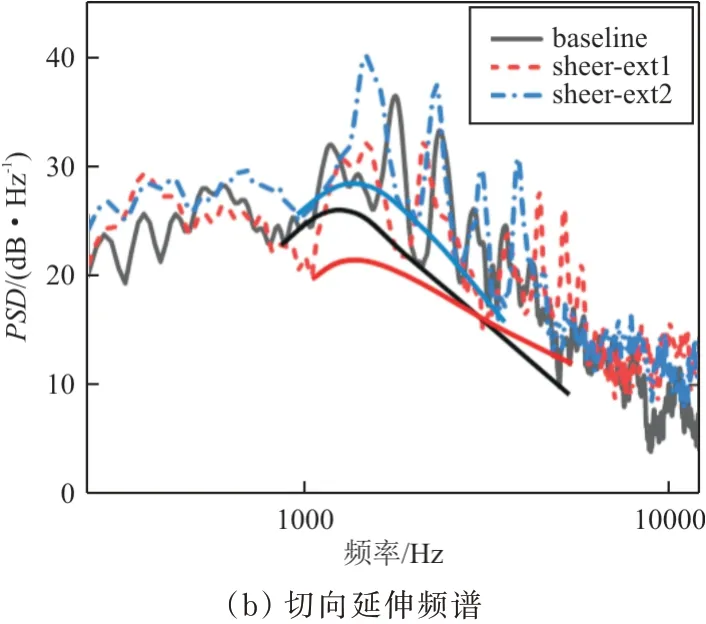
图14 远场噪声频谱对比Fig.14 Spectra contrast of Far-field noise
综上所述,远场噪声辐射水平与延伸方式、长度密切相关;且沿剪切层方向延伸具有更好的降噪效果。
3.4 流动结构与噪声源特性
Powell的涡声理论认为,低速条件下涡是产生噪声的原因[28],流场中涡结构的运动规律对噪声辐射具有重要作用。本文利用瞬态流场结构分析方法,研究涡结构在时间和空间的发展历程;通过提取涡核位置及涡结构在各种状态下的特性参数,探索缝翼尖端延伸对流场及噪声的影响机理。
基于∇2ρ的缝翼瞬态流场结构纹影图如图15所示。其中,对于基准结构尖端处(图15(a)),气流分离形成较薄剪切带状结构,在Kelvin-Helm⁃holtz不稳定性作用下卷起形成自由涡。相邻涡之间配对融合形成空间尺度更大的涡结构,与外部气流的掺混效应使临近涡合并,剪切层流向厚度不断增加,涡结构不断膨胀、破碎,直至与缝翼尾缘壁面碰撞形成离散涡。

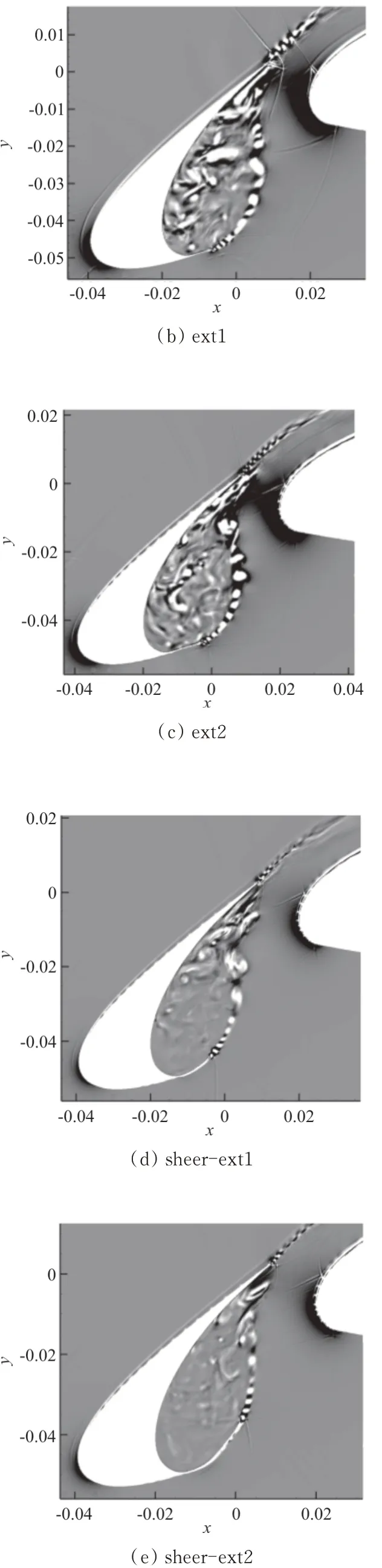
图15 缝翼∇2ρ纹影图Fig.15 Slatted schlieren diagram
缝翼尖端延伸处(图15(b)~图15(e))气流分离直接形成涡,且其特征尺度(涡结构半径与涡间距离)相比于基准结构均有减小,尤其沿剪切层方向延伸减小幅度较大,这在一定程度上削弱了剪切层中涡结构包含的能量。对于切向延伸(图15(b)~图15(c)),由于其延伸的导向作用,一方面使涡运动轨迹向主翼偏离,增加了涡的数量,回流区也存在较强的涡结构;另一方面涡流与缝翼尾缘撞击区域接近尾缘,其气流速度较大,增加了离散涡动能,这些都会导致噪声源分布增大。
对于剪切层方向延伸(图15(d)~图15(e)),气流分离形成涡的特征尺度有较大幅度地减小,涡结构的能量强度相对较弱;同时,涡的运动轨迹明显缩短,这使得其轨迹上的整体涡结构分布范围减小,涡之间“兼并”生长现象相应地减弱;另外回流区的涡结构相对较少,这些都减弱了缝翼噪声源的形成。
为了明确尖端延伸对流场结构及噪声辐射的影响。基于M.Terracol等[28]低频窄带噪声预测方法,分析缝翼流场中的大尺度涡结构的相关参数对窄带噪声源的影响规律。
每隔20个时间步长提取流场快照,作出∇2ρ纹影图。利用涡核移动距离,确定涡结构的平均对流速度(Uv);测量声波反馈距离,即涡与缝翼尾缘碰撞位置到缝翼尖端的距离(La),以及剪切层长度(Lv)。缝翼窄带噪声频率可表示为
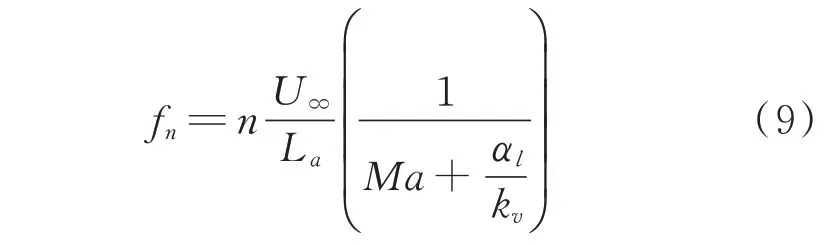
涡间距与涡半径为剪切层中部位置的统计平均值如表1所示,频率为基频(n=1),可以看出:尖端延伸可使剪切层涡半径较于基准构型有所减小,尤其是沿剪切层方向延伸情况(减少近58%)。较小涡半径其涡能量也较小;同时,涡间距也有不同程度减小(剪切层方向比切向延伸的减小幅度更大,约63%);而切向延伸(ext2)的平均对流速度增大约17%,说明切向延伸其单位时间涡与缝翼尾缘撞击的能量较大,这可能是导致宽带噪声声压级有所升高的根本原因。沿剪切层方向延伸,其涡半径、涡间距以及对流速度均明显减小,这样,单位时间涡与缝翼尾缘撞击的能量也会显著减小;同时发现,尖端延伸均会使窄带峰值右移,其中沿剪切层方向延伸会使峰值右移约6.2%左右。

表1 流场结构参数及窄带噪声频率预测表Table 1 Prediction table of flow field structure parameters and narrow band noise frequency
4 结论
(1)本文提出的缝翼尖端沿剪切层方向延伸和沿壁面切向延伸两种方式的流场与噪声辐射特性显示,缝翼尖端不同延伸方式可较大程度改变缝翼剪切层的形成与发展形态,适当的延伸形式有利于减小缝翼噪声辐射。
(2)沿剪切层方向延伸使缝翼凹腔的湍动能与涡量强度显著减小;剪切层上涡结构可在较长区域保持良好的二维特性,使宽带噪声显著减小,具有较好地降噪效果。
(3)切向延伸会增加剪切层的运动轨迹,涡流与周围气流较强的掺混效应在一定程度上也增加了远场噪声辐射。延伸长度的增加会使远场噪声更大。
(4)瞬态流场结构和低频窄带噪声分析显示,缝翼尖端延伸可改变气流分离后的涡结构特征尺度。如切向延伸在一定程度上使涡核间距和涡结构半径减小,但使涡平均对流速度增大;而沿剪切层方向延伸则可显著减小涡结构半径和涡间距,并减小对流速度。涡结构特征尺度会直接影响缝翼噪声辐射性态。较小的涡间距、涡半径以及涡流速度,其相应的缝翼噪声辐射也较小。

