基于两层POD和BPNN的翼型反设计方法
李春娜,贾续毅,龚春林
(西北工业大学空天飞行技术研究所,西安710072)
0 引言
在气动优化设计中,CFD方法由于具有高可信度而逐渐得到广泛应用[1-2],但是大量的CFD分析所消耗的时间和计算资源也是十分巨大的。为了有效地降低优化成本,研究人员提出了一系列更高效的优化设计方法,例如,使用伴随方法可以有效地提高多设计变量梯度优化过程的效率[3-4]。但是从优化算法本身进行改进仍不能有效地解决调用大量CFD的问题。
代理优化算法[5-6]的应用使CFD的调用次数呈量级式下降,大幅提高了优化效率。例如,韩少强等[7]使用梯度增强型Kriging模型实现了高维设计变量的气动反设计;邱亚松等[8]使用本征正交分解(Proper Orthogonal Decomposition,简称POD)和Kriging/RBF代理模型实现了对变外形的翼型定常流场的预测。但是,Kriging等代理模型一般只适用于单输出,对于流场参数预测等多输出问题建模效率低下。
近年来,研究人员将机器学习方法应用于流场预测、气动优化等方面,并取得显著成效[9-11]。Zhu Linyang等[12]使用RBF神经网络建立了数据驱动的湍流模型并实现了涡黏的预测;刘凌君等[13]使用反向传播神经网络(Back Propagation based Neural Network,简称BPNN)构建了翼型参数化系数与翼面压力系数的神经网络,并实现了翼型反设计,但存在模型训练样本量大(4 000个训练样本),需要将翼型参数化系数分组建立多个神经网络等复杂问题。
直接使用神经网络(Neural Network,简称NN)构建流场预测模型,由于流场数据维度高,模型输入输出维度差异过大,导致模型学习缓慢、建模困难。而以POD为代表的降阶模型可以有效地解决高维数据的维度灾难问题,并已成功应用于流场近似求解、翼型反设计等方面[14-15]。
本文以翼型为研究对象,首先,结合POD和NN的特点,发展一种基于两层POD和BPNN的翼型反设计方法;然后,将该方法应用于亚/跨声速下的翼型反设计,包括翼型库建立、聚类取样、基模态个数选取、模型训练等方面;最后,通过算例对预测误差、聚类取样效果和超参数等方面进行分析。
1 建模方法
1.1 样本库建立
常见的翼型参数化方法包括Hicks-Henne、CST、PARSEC、B样条等[16-17],其中Hicks-Henne参数化通过在基准翼型的上下表面叠加数个Hicks-Henne形函数,并调节形函数的个数、作用位置、高度系数来实现翼型外形的改变,在翼型反设计、气动优化设计中得到广泛应用。
本文以典型的亚声速翼型NACA0012和跨声速翼型RAE2822为基准翼型,在其上下翼面各施加6个Hicks-Henne形函数,其高度系数范围在亚声 速 中 为[±0.005,±0.010,±0.010,±0.010,±0.010,±0.005],在 跨 声 速 中 为[±0.005,±0.005,±0.005,±0.005,±0.005,±0.005],对应的作用位置均为0.10c、0.25c、0.45c、0.65c、0.80c、0.90c(c为翼型弦长)。
1.2 POD降阶
POD是将具有高维特征的数据转化为正交的低维特征数据。为了最大程度地保留原始数据的信息量,应使降阶后的数据方差最大化[18]。
设r个样本构成原始样本数据矩阵X=每 个 样 本 为n维 向 量,即对X做中心化处理,得到新样本数据D=其中

使用线性映射矩阵U(m×n)将D降 阶 至m维 空间,降阶所得数据为Y(m×r),即

要使Y方差最大化,只需计算D的协方差矩阵var(D)的特征值和特征向量,并将前m个最大的特征值所对应的特征向量q1,q2,…,qm构成U即可。var(D)的计算公式为
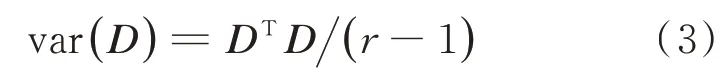
式中:DT为D的转置矩阵。
POD降价流程如图1所示。

图1 POD降阶流程Fig.1 Process of building POD reduced-order model
1.3 BPNN模型
BPNN是一种通过前向传播计算输出,反向传播计算误差的全连接神经网络。其特点是多输入多输出建模,具备较强的非线性拟合能力,普遍应用于分类或回归问题[19]。典型的BPNN具有三层:输入层、隐藏层和输出层,如图2所示。

图2 三层BPNNFig.2 A BPNN with three-layer
对于如图2所示的BPNN模型,输入层为m个神经元,输出层为n个神经元,隐藏层神经元个数为q,其大小由m、n值确定,这里q=max{m,n}。每层神经元通过权值ω和激活函数连接[19],本文算例中隐藏层和输出层的激活函数类型分别为tansig和purelin函 数,BPNN的 训 练 流 程 如 表1所示。

表1 BPNN的训练流程Table 1 Training process of BPNN
1.4 翼型反设计方法
结合POD和BPNN模型,发展一种快速的翼型反设计方法,其流程图如图3所示。具体流程分为四步。

图3 基于两层POD和BPNN的翼型反设计方法Fig.3 Airfoil reverse design method based on two-layer POD and BPNN
第一步,翼型库建立。
使用参数化方法得到r个不同几何外形的翼型(无量纲化),每个翼型可以用坐标集表示,其中x0为构成翼型的所有坐标点的横坐标,每个翼型均相同;yi为构成第i个翼型的所有坐标点的纵坐标。因此,每个翼型可以由唯一的yi确定。使用流场求解器,可以计算给定工况下每个翼型所对应的翼面压力系数。第i个翼型对应的翼面压力系数用{xC,Ci}表示,其中xC为描述上下翼面所有点的横坐标值,且每个翼型均一致;Ci为第i个翼型的翼面压力系数值。因此,每个翼型的翼面压力系数可以由唯一的Ci确定。
第二步,确定样本集。
在建立翼面压力系数到几何外形的映射之前,为了确定最佳训练样本量,提高训练效率,本文提出一种聚类取样策略。首先将所有样本的翼面压力系数C进行POD降阶,得到压力系数的基模态系数矩阵将基模态系数一致的样 本 归为一类Si(i=1,2,…,k,且k<r),每类 随机抽取一个样本Ci=∀Si作为训练集中的样本,训练集为从剩下的(r-k)个样本中随机抽取t个样本作为测试集
第三步,模型建立。
训练集的k个样本,其压力系数为CT(n1×k),几何外形(纵坐标)为yT(n2×k),对压力系数和几何外形分别建立POD模型,命名为POD 1和POD 2,得到对应的基模态系数矩阵YC(m1×r)和Yy(m2×r),其中m1和m2满 足m1≪n1、m2≪n2,其 大 小 通 过 分 析POD重构误差确定。此后,将YC和Yy分为作为BPNN的输入和输出来训练BPNN模型。其中,BPNN为三层,输入层为m1维,输出层为m2维,隐藏层神经元个数为max{m1,m2}。
第四步,翼型反设计。
任意选取测试集中的样本,其对应的压力系数为Cs。首先,通过POD 1模型得到压力系数的基模态系数YC s;然后,带入训练好的BPNN,得到预测几何外形的基模态系数Yy s;最后,通过POD 2重构得到预测的几何外形ys。从而快速实现翼型反设计。
2 算例与分析
2.1 翼型库建立
采用Hicks-Henne参数化方法,计算工况为亚声 速 状 态:Ma=0.35、α=2.79°、Re=6.5×106;跨声速状态:Ma=0.75、α=2.79°、Re=5.7×106,流 场 求 解 器 分 别 为Xfoil[13]和Fluent。以NA⁃CA0012翼型求解为例,对比Xfoil与Fluent得到的翼面压力系数分布,如图4所示,可以看出:两者基本吻合,说明Xfoil在小攻角亚声速计算状态下具有较高的准确性。而后,利用拉丁超立方试验方法生成500个翼型样本,并通过流场求解器计算500个新翼型的压力系数,得到压力系数矩阵C。
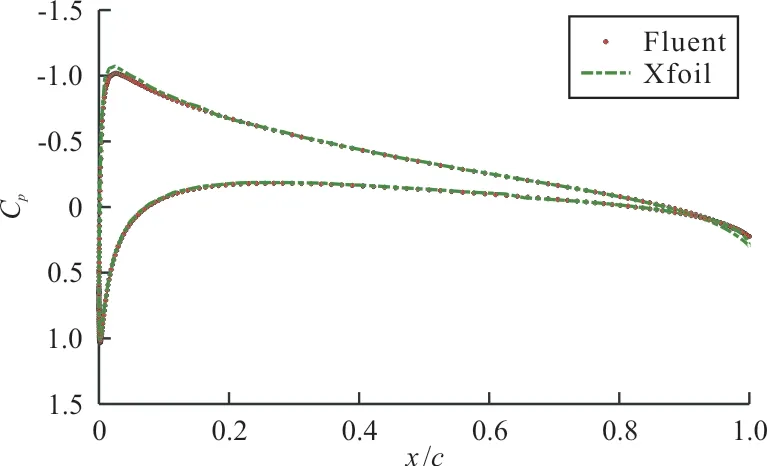
图4 NACA0012翼型翼面压力系数分布对比Fig.4 Comparison of pressure coefficient distribution of NACA0012
2.2 聚类取样
定义重构(或预测)误差为

式中:e1为均方根误差;e2为均方误差;分别为第i个坐标位置的预测数据和真实数据,该数据在POD 1中表示压力系数,在POD 2中表示几何外形纵坐标;N为总坐标位置数目。
对压力系数C随机抽取90%进行POD建模,10%进行POD重构误差分析。不同基模态个数取值下压力系数的重构误差如图5所示,可以看出:可以发现,压力系数的信息主要集中在前11阶:基模态个数小于11时,重构误差随着基模态个数增加减小得非常快;当基模态个数继续增大时,重构误差的下降程度变缓,并逐渐接近0。当基模态 个 数 取20时,亚 声 速e1=3.7×10-3,e2=1.39×10-5,跨 声 速e1=3.0×10-3,e2=9.97×10-6,误差很小,因此压力系数的降阶维数s1设为20。


图5 压力系数的重构误差Fig.5 Reconstruction error of pressure coefficient
采用K-means算 法[18]对500组压力系 数的基模态系数(20阶)进行聚类分析,聚类数目设置为200。根据1.4节的第二步,可以得到200个训练样本。再在剩余样本中随机抽取10个作为模型的测试样本。
2.3 模型训练
使用与2.2节相同的方法确定几何外形的基模态个数取值。随机抽取训练样本的90%,并对其几何外形建立POD 2模型,然后对另外10%进行重构误差分析,得到几何外形的重构误差如图6所示。

图6 几何外形的重构误差Fig.6 Reconstruction error of geometry
从图6可以看出:当基模态个数为12时,亚/跨声速的均方根误差e1基本接近于0,说明前12阶基模态可以高精度地重构出几何外形。
对比图5和图6,可以看出:跨声速的重构误差小于亚声速,这是由于在Hicks-Henne参数化中跨声速的参数范围小于亚声速所致。
此时,确定了BPNN模型的输入和输出维度分别为20、12,取隐藏层神经元个数为20,训练并建立从压力系数的基模态系数到几何外形的基模态系数的网络。由于训练样本量小(200个),且BPNN模型仅为三层,模型训练耗时很短。在In⁃tel i5-8500 CPU、16G RAM的PC上,聚类取样耗时约为0.5 s,POD 1和POD 2的建模耗时均不到0.2 s,BPNN训练耗时为5~8 s,整个模型的建模时间相对于流场求解时间是很短的。
2.4 结果分析
在某计算工况下,给定目标压力分布,获得满足该压力分布的翼型的过程称为翼型反设计[20]。在亚/跨声速下,分别对于所选取的10个测试样本,将其压力系数作为模型输入,使用两层POD+BPNN模型,预测出对应的翼型,并与目标翼型的外形进行对比,得到均方根误差分布如图7所示。
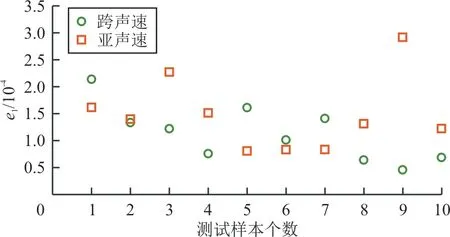
图7 翼型反设计的均方根误差Fig.7 RMSEs of inverse-designed airfoils
取亚/跨声速中误差最大的第9个和第1个测试样本,对比其目标翼型与预测翼型,如图8所示。对比预测翼型的压力系数与目标压力系数,如图9所示。
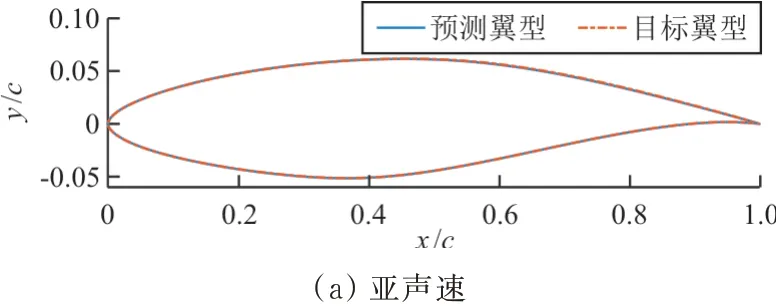
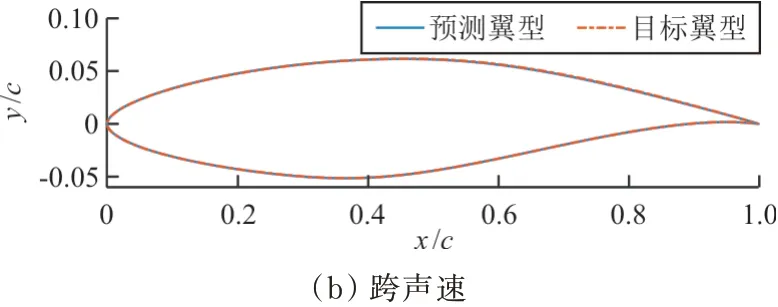
图8 目标翼型和预测翼型的对比Fig.8 Comparison of real and predicted airfoils

图9 目标和预测压力系数的对比Fig.9 Comparison of real and target pressure coefficient
从图8~图9可以看出:预测翼型与目标翼型无明显差异,且预测翼型的压力系数与目标压力系数曲线吻合较好,说明在亚/跨声速工况下,两层POD+BPNN模型的精度能够满足翼型反设计的要求。
同时,以亚声速为例,将预测翼型与目标翼型的纵坐标做差,得到上下翼面翼型外形的预测误差Δ1;将预测翼型的压力系数与目标压力系数做差,得到上下翼面压力系数的预测误差Δ2。两个误差如图10所示,可以看出:翼型纵坐标的预测误差的量级为10-4,而翼型纵坐标的量级为10-2;压力系数的预测误差的量级为10-2,而压力系数的量级为100,说明使用该模型进行翼型反设计具有较高的准确性,且预测翼型的翼面压力系数分布与目标压力系数分布相一致。
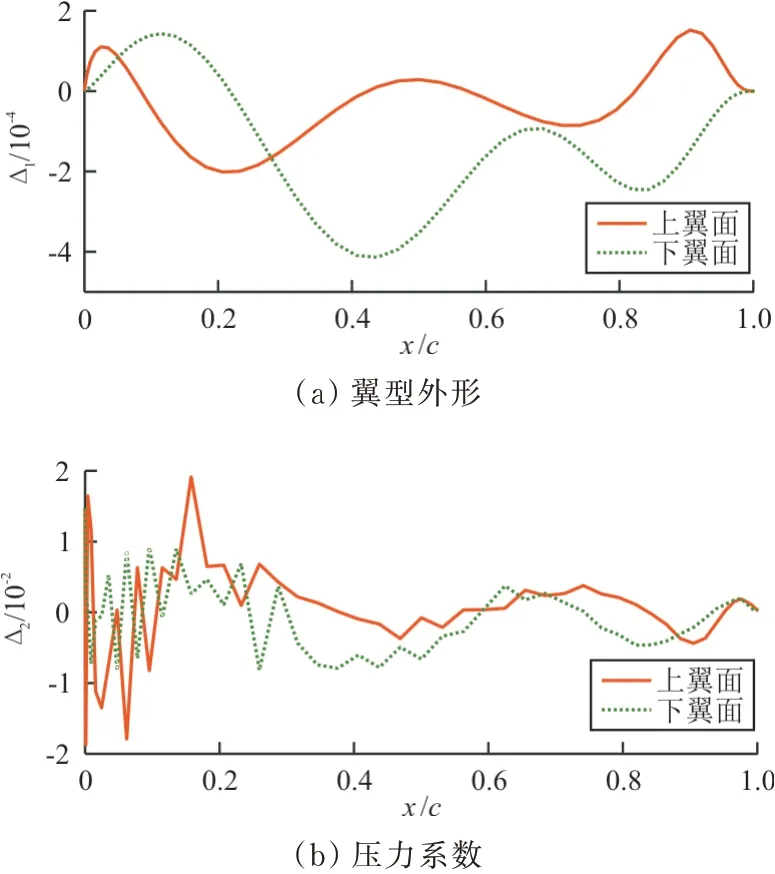
图10 翼型外形和压力系数的预测误差Fig.10 Prediction errors of airfoils and pressure coefficients
上述模型是由聚类取样得到的200个样本训练所得,为了进一步分析训练样本量对模型预测精度的影响,选取聚类数目k∈[20,490],并随机取10个样本作为测试集,得到亚/跨声速下、不同k下10个测试样本的预测翼型外形与真实翼型外形的均方根误差均值e1随k的变化规律如图11所示,可以看出:聚类数目小于120时,随着聚类数目的增加,均方根误差下降很快,说明训练样本量过少不能够表征出全部样本的特征;当聚类数目达到180以上,均方根误差处于较低水平,继续增加聚类数目不会使均方根误差产生明显变化,说明聚类取样得到的180个样本基本可表征出全部样本的特征。本文选取200个样本建模是合理的。
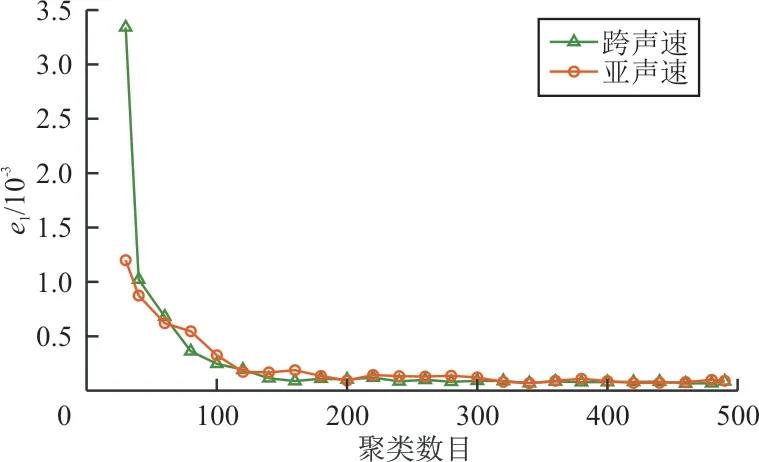
图11 聚类数目对模型预测误差的影响分析Fig.11 Influence of the of cluster number on the model error
2.5 超参数分析
BPNN的超参数包括网络层数、隐藏层的神经元个数、激活函数类型、训练函数类型、学习率等,这些超参数会影响模型的训练效率、预测精度。本文针对跨声速算例,以隐藏层神经元个数和激活函数为例,分析超参数对模型训练的影响。
(1)隐藏层神经元个数
通过设置不同的隐藏层神经元个数,分析模型的预测误差和训练耗时,如图12所示。

图12 隐藏层神经元个数对模型训练的影响分析Fig.12 Influence of the number of hidden layer neurons on model training
从图12可以看出:当神经元个数小于10时,预测误差较大,说明在本问题中,隐藏层神经元个数过少不能够完整地学习到样本的特征;当神经元个数取值在10~50之间,预测误差基本一致,但是训练耗时会随着神经元个数的增多呈现上升趋势。因此,隐藏层神经元个数的取值应适当。
(2)激活函数
选取6种不同的激活函数组合,分析不同组合下模型的训练耗时和预测误差,如表2所示,可以看出:使用“tansig+purelin”和“logsig+purelin”均能保证较高的训练效率和预测精度。

表2 不同激活函数组合对模型训练的影响分析Table 2 Influence of the different activation functions on model training
3 结论
(1)本文发展了一种基于两层POD+BPNN的翼型反设计方法,可以高效地建立从高维翼面压力系数到高维翼型外形的映射。
(2)通过对压力系数的基模态系数聚类来确定样本集,可以在保证模型精度的前提下有效地降低训练样本量,提高建模效率。
(3)针对亚/跨声速算例,使用200个样本建立的两层POD+BPNN模型,其预测翼型外形的均方根误差为10-4量级,对应的压力系数与目标压力系数吻合很好,说明该模型的精度可以满足翼型反设计的要求。

