基于增广Burgers方程的超声速客机远场声爆预测研究
崔青,白俊强,宋源,余培汛
(1.航空工业空气动力研究院气动研究与试验一部,沈阳110000)
(2.西北工业大学 航空学院,西安710072)
0 引言
超声速客机能够有效地缩短长距离飞行所花费的时间,提高出行效率,其优点在越洋出行中更加明显。因此各大国和国际机构对于超声速客机的研究一直没有中断,而如何降低超声速客机的声爆水平和超声速客机的航线规划也一直是限制超声速客机投入大规模应用的瓶颈[1]。如何精确预测声爆强度是其中的关键技术,全场直接计算法因其过于耗费计算资源,目前没有工程实用价值[2]。近场CFD计算与远场声学传播计算相结合的方法是目前国际上常采用的高精度声爆预测方法。其中远场声学传播计算的方法主要分为波形参数法[3]和Burgers方程法[4]。
波形参数法所求得的远场过压波形中,激波是间断的,且不包含激波上升时间,进行声强级计算前需依据实验数据进行人工激波增厚;波形参数法并没有考虑大气湿度的影响,模型具有理论缺陷[5]。但Burgers方程在求解过程中考虑了大气湿度带来的影响以及还有其他效应,求解远场过压的同时能求解激波上升时间。
国外对Burgers方程的研究较早,由于Burgers方程模型比较简单,只能预测有限振幅平面波在热黏性耗散介质中的传播。这种简单模型只能模拟传播过程中的非线性效应和热黏性吸收效应,被称作经典Burgers方程[6],之后有研究者提出了广义Burgers方程[7]。和经典Burgers方程相比,广义Burgers方程加入了传播过程中几何扩散效应和大气分层效应的模拟。广义Burgers方程的进一步发展就是增广Burgers方程,增广Burgers方程在广义Burgers方程的基础上加入了对分子迟豫效应的模拟[8]。至此,Burgers方程对声爆传播过程的模拟基本完善。现在常说的增广Burgers方程是一个复杂的偏微分方程,右端有五项,包含之前提到的五种效应,对其进行整体的离散和数值求解有一定难度。直到1995年,R.O.Cleveland[9]提出了算子分裂法,该方法最早被Y.S.Lee和M.F.Hamil⁃ton用于求解KZK方程[10]。算子分裂法的 核心便是在小推进步长上依次单独离散求解右边的每一项,每一项求解的结果作为下一项求解的输入,经验证这种算法的计算结果收敛于整体离散求解的结果[11]。大量基于增广Burgers方程的声爆预测程序均采用了Cleveland的算子分裂法[5,12],但对于整体求解的探索并没有停止。2015年,M.Yama⁃moto等[13]提出了一种使用内部变量的变换,经过这种变换,右侧项可以联合求解,和算子分裂法相比,这种算法更加稳定且计算速度更快;S.Rallab⁃handi[14]主 要 将 精 力 集 中 在Burgers方 程 和 外 形 优化相结合,同时探究了传播过程中因地球三维效应带来的影响[15],研究结果显示三维效应对于无风大气中的传播没有太大影响,但当大气风速存在时,三维效应对于传播路径会有较大影响,甚至会得到与无风大气相反的结论。
近年来,国内也有不少研究者对增广Burgers方程开展了较深入的研究。张绎典等[4]构建了基于增广Burgers方程的远场求解方法,利用第二届国际声爆研讨会(SBPW-2,简称:大会)给出的标准算例对其精度进行了验证,同时探究了近场过压信号的时间采样频率和远场信号波形失真程度的关系,为了保证波形不发生过分的失真,信号的采样频率不应低于85 kHz,对大气湿度与远场过压峰值的关系进行了初步研究;乔建领等[16-17]构建了基于增广Burgers方程的近远场结合的声爆预测方法,利用大会给出的标模算例对近场、远场的求解精度均进行了验证,最后基于该预测方法,探究了风速对声爆幅值和地面影响区域的影响,但是在相同推进步长情况下,激波插入精度有待提高。
本文探究基于增广Burgers方程的声爆预测方法的求解过程,提出一种有效的非线性效应求解方法;在算子分裂法的基础上构建声爆远场预测方法,基于该方法编写声爆预测程序,通过该程序计算大会的两个标准算例[18-19]以验证该程序的正确性;分析空间、时间网格密度及缓冲信号对预测结果的影响。
1 方程求解
增广Burgers方程来源于经典Burgers方程,其有量纲形式如式(1)所示。式中:x为从出射点开始的声线传播距离;p′为声爆信号有量纲过压;t′为延迟时间,是为了得到行波解而建立的新时间坐标系下的时间;ρ0,c0分别为巡航高度处于受扰动大气密度与声速;β,b分别为非线性效应系数和热黏性吸收效应系数。
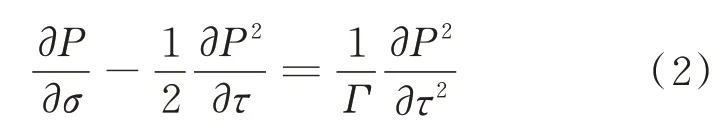
式中:σ为无量纲声线传播距离;-x为激波形成距离为无量纲压力;p0为参考压强,一般取巡航高度处的静压;τ为无量纲延迟时间;ω0为输入波形的角频率,通过将输入的波形看作一个周期求得;Γ为无量纲热黏性系数,当Γ变大时,非线性效应逐渐占主导地位,当Γ变小时,热黏性吸收效应逐渐占主导地位。
经典Burgers方程只包含非线性效应项与热黏性效应项,添加几何扩散效应项和大气分层效应项后便得到广义Burgers方程,其无量纲形式如式(3)所示。
式中:S为声线管截面积。
在广义Burgers方程中添加分子弛豫效应项,便得到增广Burgers方式,形式为

式中:Cv为第v个弛豫过程的无量纲色散系数;θv为第v个弛豫过程的无量纲弛豫时间。
式(4)中右侧项依次为非线性效应项,热黏性吸收项,分子弛豫项,几何扩散项效应和大气分层效应项。根据算子分裂法,式(4)被分解为下列形式:

按照算子分裂法,求解时由上至下依次求解式(5)每一项,将式(5)中上一项的结果作为下一项的输入,每将上述五项遍历一次等同于在真实空间中推进一步。推进时沿声线传播方向推进直至到达指定高度即可。
式(5)第一项为非线性效应项,用于计算由于传播中非线性效应累积导致的波形畸变,该效应是声爆波形在传播中变化的主要原因。
式(5)第二项为热黏性吸收效应项,用于计算由于分子间摩擦导致的信号强度衰减。
式(5)第三项分子弛豫项与其他几项形式上有一点差别,因为不同气体分子弛豫效应不同,大气整体弛豫效应与不同种类气体占比有关,因此该项需要将所有与大气整体弛豫效应有关的气体进行计算。真实大气中对弛豫效应影响较大的气体有氮气、氧气、二氧化碳和水蒸气。其中二氧化碳和水蒸气由于在大气中含量远小于氮气与氧气含量,在弛豫效应计算中可被略去,但需要注意大气湿度对氧气与氮气弛豫效应的影响没有被忽略。因此第三项实际上是两项求和的形式,出于简化离散求解的目的,求解弛豫效应时依旧采取算子分裂法,即将氮气与氧气的弛豫效应分开计算,上一项的结果作为下一项的输入,经算例验证该算法能正确模拟大气整体弛豫效应。
式(5)第四项为几何扩散效应项,用于计算声爆传播过程中由于波振面扩大导致的衰减。受大气分层的影响,声爆信号的传播路径一般不是直线,因此衡量几何扩散效应与信号的传播路径有关。常用方法是选取信号发生处相邻的四条声线,这四条声线围成一个管道,用与其中一条声线垂直的平面与声管所截得的面积作为该处声线管面积。每推进一步会得到每一步的声线管面积,用每一步的声线管面积变化即可衡量传播中的几何扩散效应。
式(5)最后一项为大气分层效应项,用于计算由于大气参数如密度、温度等随高度变化导致的信号强度衰减。
其中除去非线性效应外,文献[9]中已有详细的离散和求解方法,本文不再赘述。
1.1 非线性求解
与普通声波的传播不同,声爆的过压值并不远小于大气静压值。声爆在传播过程中受到累积的非线性效应作用,波形会发生扭曲变形[20]。描述这种情况的解析解为Poisson解,具体形式如式(6)所示。

为了便于求解,将波形转换到扭曲时间坐标下。

将式(7)代入式(6),得到:

即只要将波形转换到扭曲时间坐标下,就能得到推进一步后的波形。为了后续计算方便,可将波形线性插值到均匀时间坐标。当推进步长过大或累积推进一定距离后,会出现多值现象,如图1所示。

图1 波形的多值现象Fig.1 Multivalue form of the wave shape
在真实传播过程中并不会产生多值现象,非线性效应导致的波形扭曲,堆积会产生激波,进而消除多值现象。计算中需要插入激波来消除多值现象,激波插入位置可以使用面积相等原则[20]求得,如图2所示,激波插入的位置使得激波所在直线和波形围成的两部分面积相等。实际插入激波情况和图2类似,如图3所示。
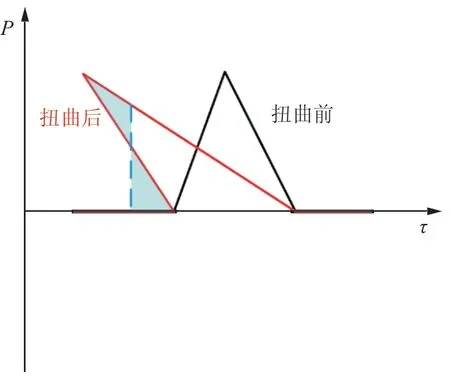
图2 激波插入位置示意Fig.2 Position of the inserted shock wave
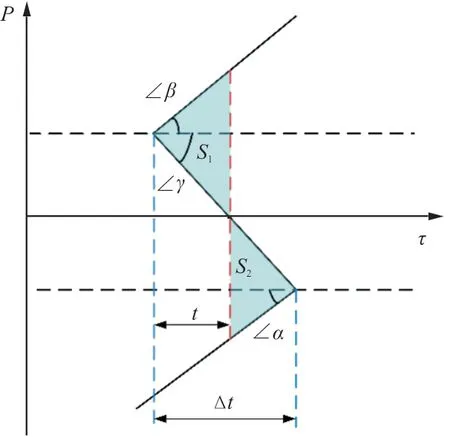
图3 实际插入激波情况Fig.3 Insertion in reality
由面积相等原则可以得到S1=S2,虽然波形多值部分一般不会是折线,但用折线和三角形面积进行近似能满足精度需求。推进步长不能过大,否则多值部分波形会更复杂以致不能使用折线和三角形面积进行近似,如图4所示。如果继续按三角形面积计算,所得过压值会很快发散。

图4 推进步长过大导致失效Fig.4 Long step causing failure
1.2 声线追踪及声线管面积
根据文献[9]的理论,在均匀无风介质中声爆沿直线传播,声速沿高度线性分布时,声爆沿一圆弧传播。真实大气存在分层效应和风速梯度,且声速一般不会沿高度线性分布,此时声线将会是一条任意曲线。如果不存在垂直方向风速,根据几何声学理论[21-22]声线追踪可按式(9)~式(10)计算。

式中:R为声线位置矢量;W为当地风速向量;N为波阵面单位法向量;I为单位矩阵;⊗为克罗克内积。

式中:Δt为相邻两推进步之间传播所用的时间,Δt=Δz c0Nz;Δz为相邻两推进步之间声线传播距离;Nz为在这两部间声线波阵面单位法向量。
N需要在每次推进过程中更新,N更新需要Δt。但没有N就不能求得Δt,如果推进步长足够小,可以将上一步的N近似作这一步的N。本文采取一种预估—校正的方法进行声线追踪。首先设定一Δz,用上一步N和设定的Δz求得Δt;然后用该Δt计算出真实推进距离Δz,再进行高度更新;重复此步骤直到声爆传播到希望高度。使用该方法可以避免波阵面单位法向量N的近似带来的误差,同时可以适当放大推进步长。
声线管是由四条相邻的声线所围成的“管”,这 四 条 声 线 分 别 从(ta,φ),(ta,φ+Δφ),(ta+Δta,φ),(ta+Δta,φ+Δφ)这四个位置出射,位置关系如图5所示。

图5 声线及声线管面积示意Fig.5 Definition of ray and ray tube area
分别计算出这四条相邻声线在同一推进步时的位置坐标后,可以根据式(13)求得声线管面积。
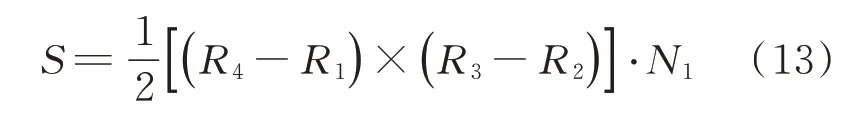
1.3 计算流程
计算声爆的程序框架如图6所示,其中输入分为三部分:过压信号输入,风速输入和大气参数输入。如果不输入风速和大气参数,计算将采用内置的无风标准大气[23]。输入过压信号必须是无量纲化的过压信号。

图6 程序计算流程图Fig.6 framework of the program
将过压信号插值到均匀、无量纲的时间网格上,根据当前高度计算出对应大气参数,再按照上述射线追踪与面积计算方法更新声线坐标和声线管面积。接下来依次单独计算非线性效应,热黏性吸收,分子弛豫效应,几何扩散效应和大气分层效应。如果推进到指定高度(比如地面),程序停止,输出结果;如果没有推进到指定高度,重复上述过程直到指定高度。
采用指定有量纲推进距离再预估—修正的方法确定每次推进步长。当剩余高度不足指定距离时,将剩余高度无量纲化作为最后的推进步长代入程序计算。
2 标模验证
在展示标模验证结果之前,需要明确信号提取位置与指向的定义和风速与机头指向的定义,再展示标模验证的结果。
2.1 提取位置与指向
提取位置及指向角示意图如图7所示,即从飞机飞行正前方向后看去的视角。图中虚线圆弧代表空间中距离飞机一定距离的圆柱面,近场信号在该面上提取[24]。提取距离一般用H L来衡量,H为提取位置距离飞机的距离,L为飞机长度。H L选取既要保证近场信号收敛,又不能过大,避免浪费时间。
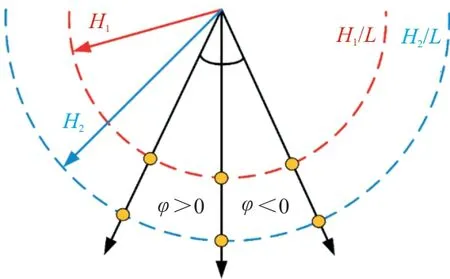
图7 提取位置及指向角示意图Fig.7 Definition of extract position and pointing angle
飞机飞行的方向与正北方的夹角α如图8所示,该角度用于将声速表中沿正北、正东向的风速转化到以飞机飞行方向为x正向的坐标系下。更新声线坐标等计算均在该坐标下进行,该坐标为右手坐标系,当飞机向正东方飞行时,x轴正向为东,y轴正向为北,z轴正向向上。
2.2 LM1021标模验证
LM1021是SPBW-2中远场计算的标模算例之一,原型为洛克希德马丁公司的一款超声速客机,实验模型外形如图9所示。

图9 LM1021外形[25]Fig.9 Shape of LM1021[25]
第二届国际声爆研讨会提供了风洞实验数据[26]和远场数据[27],提取位置H L=3.129 9,分别提取出射角为0°,30°的信号(如图10所示)。

图10 LM1021近场输入信号Fig.10 Farfield signature of LM1021
对应的巡航高度为16 764 m,巡航马赫数为1.6Ma,地面反射因数取为1.9,侧滑角为0°,大会提供了多个大气情况和风速表供选择,本次选择标准无风大气进行验证,0°和30°远场波形对比如图11~图12所示。

图11 0°远场波形对比Fig.11 Comparison of farfield waveform of 0°

图12 30°远场波形对比Fig.12 Comparison of farfield waveform of 30°
图11 ~图12中,cal表示本程序计算结果,sboom表示大会程序提供的标准结果,可以看出:计算结果与大会提供标模值吻合良好。
2.3 C25D标模验证
C25D是SPBW-2中的近场计算算例[28](如图13所示),但各参与者均进行了远场传播计算,大会也给出了重新插值后的标准过压提取值。本文选用Aftosmis[29]的计算结果作为标准进行算例验证,计算结果如图14~图16所示,其中,巡航高度为15 760 m,巡航马赫数为1.6Ma,地面反射因数为1.9,侧滑角为0°。

图13 C25D外形Fig.13 Shape of C25D

图14 C25D近场输入信号Fig.14 Extracted signature of C25D

图15 0°远场波形对比(C25D)Fig.15 Comparison of farfield waveform of 0°(C25D)

图16 30°远场波形对比(C25D)Fig.16 Comparison of farfield waveform of 30°(C25D)
从图14~图16可以看出:计算结果与大会提供结果吻合良好,程序计算精度满足要求。
3 缓冲信号的设置
在计算LM1021的远场过压信号时,如果采用大会提供的原始输入信号,会发生激波上升时间不足和过压幅值不足的情况。张绎典等[4]指出,如果在原始信号前加入一段过压值为0的缓冲信号,情况会得到解决。
本文对该现象进行分析,在LM1021,C25D的原始信号前分别加入了长度为0.1 s,0.04 s的缓冲信号(长度约为原始信号长度1/5)作为对比,如图17~图18所示,图中extended表示添加缓冲信号后的结果,original表示未添加缓冲信号的结果。需要说明的是,两者原始信号在首尾已有一定长度的缓冲信号,即在添加缓冲信号前便是延展信号。

图17 LM1021添加缓冲信号与否对比Fig.17 Comparison of LM1021 before and after adding signature

图18 C25D添加缓冲信号与否对比Fig.18 Comparison of C25D before and after adding signature
从图17可以看出:在加入缓冲时间后LM1021远场信号大有改善,激波上升时间和过压幅值达到与大会提供结果一致的水平。从图18可以看出:缓冲信号的加入与否并不影响激波上升时间和过压幅值。
在模拟声爆传播过程中,需要人工插入激波,这一过程会造成波形在时间方向上延长,真实传播过程中波形也会在时间方向上延长。如果最终长度超过原始波形并且没有添加缓冲信号就会造成波形在时间轴左端“堆积”,导致结果不正确。
与C25D相比,LM1021尺寸更大,产生声爆过压值也更大,同样无量纲推进距离下波形扭曲更严重,波形在时间轴上延长情况也更严重,因此LM1021需要加入缓冲信号而C25D则不需要。
4 时间网格与空间网格密度
由于程序中采用指定采样点个数的方式确定时间网格密度,因此在探究时间网格密度时为了方便考虑,直接改变采样点个数,再转化为采样频率的方式。本文分析从小到大8个采样点对远场信号波形的影响,结果如图19所示。

图19 不同时间网格密度结果对比Fig.19 Comparison of farfield signatures of different time grid densities
从图19可以看出:在5×104和8×104个采样点的情况下,波形负值部分的形状仍在变化,但正值部分尤其是与上升时间相关的波峰形状基本固定;之后波形形状与位置基本保持不变,只会发生小范围浮动;过压峰值随着采样点个数上升而上升,上升逐渐减缓直到2.5×105个采样点后开始下降。
如果按照上述分析,在计算时应采用2.5×105个时间采样点对输入信号进行离散。但这并没有实际意义,由于计算的时间代价难以接受。对于8×104和105个采样点,过压峰值增量只相当于峰值的不到0.04%。而且从8×104个采样点后波形形状基本固定,尤其是与响度密切相关的正值部分形状在6×104个采样点后便基本固定。因此在实际计算中应根据对精度的要求选取合适的采样点个数。
对于不同的信号,尤其是不同时间长度的信号,在选取采样点个数时应关注两相邻采样点间的无量纲时间间隔和采样频率。由于采样频率是一个消除信号输入频率和时间影响的无量纲量,不同长度的信号输入频率不相同,但输入信号长度与频率相关,采用采样频率来描述更具有普适性。而无量纲时间间隔会直接参与计算,因此该响应与计算的方法与过程有较密切的关系。
由于在模拟过程中采用不同算法也会导致结果对频率的响应不同,如果采用本文的程序,C25D信号在9×104个采样点时过压峰值已经开始下降,对应的采样频率约为430 kHz,而文献[17]的计算结果则认为采样频率不应低于400 kHz。
空间网格的情况与时间网格类似,如图20所示。

图20 不同空间网格密度结果对比Fig.20 Comparison of farfield signatures of different spe⁃cial grid densities
从图20可以看出:随着网格逐渐加密,波形形状先开始固定,之后开始小幅度扰动。因此空间网格并不是越密越好,只要满足精度需求即可。与时间网格的选取相同,空间网格的密度受到计算方法的影响。如果计算方法在推进步长较大时发散便只能采用较小的推进步长,时间网格被迫加密。
5 结论
(1)本文提出了一种非线性效应求解算法,并基于算子分裂法构建了基于增广Burgers方程的声爆远场预测程序,采用SBPW-2中的标模算例验证了其有效性,其计算精度满足设计要求。
(2)为了达到所需计算精度,时间网格和空间网格密度不需取到满足网格收敛性的密度,能达到波形固定和过压峰值增长不超过预定值即可。
(3)缓冲信号对于小型飞机声爆计算来说不是必要的,但对于大型飞机来说是必要的。
(4)无量纲时间间隔会直接参与计算,具体算法会影响到波形对时间网格和空间网格的敏感程度。
(5)非线性算法受空间网格密度影响较大,为了提高计算速度应采用对空间网格密度不敏感的算法。

