基于卷积神经网络和多项式混沌方法的翼型鲁棒性优化
高远,闫妍,周磊,李典,郝海兵
(航空工业西安航空计算技术研究所 第七研究室,西安710065)
0 引言
在大展弦比飞行器气动外形的设计过程中,翼型的气动优化设计至关重要。何萌等[1]对超临界翼型RAE2822进行了优化,并研究了其中的多极值问题;陈笑天等[2]研究了针对旋翼翼型的高速综合气动优化设计方法;李春鹏等[3]针对自适应后缘翼型发展了气动优化设计方法。上述基于气动数值模拟的翼型优化设计是在确定条件下进行的,当条件受到扰动发生变化时,最优翼型的性能可能会有所恶化。为了缓解非设计点性能可能会恶化的问题,引入了翼型鲁棒性优化设计方法,在设计状态下对翼型的气动性能进行优化,同时兼顾设计点一定变化范围内气动性能的稳定性[4]。
与确定性优化设计相比,鲁棒性优化的一个显著特点是在优化过程中不断地进行不确定度量化,即计算系统关于随机变量的不确定性响应。最常用的不确定度量化方法为蒙特卡洛法,该方法是一种最简单的评估方法,可以很方便地计算响应量的概率分布,而且预测精度较高。但是对于该方法而言,若要使响应量的期望概率水平达到10-N的 要 求,样 本 点 的 数 量 至 少 应 为10N+2[5]。即便应用拉丁超立方抽样技术进行了改进,提高了分析效率,但是蒙特卡洛方法仍然具有计算样本量较大的问题。因而在翼型鲁棒性优化设计中,需要进行大量的CFD计算,计算代价很大[6]。
针对这一问题,国内外开展了广泛研究。国外,K.Zhao等[7]基于多目标进化算法对自然层流超临界翼型开展了鲁棒性优化;H.Shah等[8]发展了一种考虑混合不确定性的、多精度的翼型鲁棒性设计方法;A.S.Padron等[9]应用多可信度方法进行了翼型的气动鲁棒性优化;D.I.Papadimitriou等[10]使用一阶可靠性方法结合基于伴随的优化方法对翼型进行了考虑升力可靠性的鲁棒设计;D.Lucor等[11]提出了一种应用随机代理模型的翼型随机优化框架。国内,李焦赞等[12-13]开展了基于几何不确定性的翼型多目标鲁棒优化设计研究,在鲁棒优化设计中引入了多目标遗传算法,并考虑了马赫数波动的鲁棒优化问题;白俊强等[14]使用CST参数化方法对超临界翼型的马赫数波动鲁棒优化设计问题开展了研究;Zhao H等[15-17]建立了基于非嵌入式多项式混沌方法以及稀疏多项式混沌方法的高效翼型鲁棒性多目标优化设计方法。
上述针对翼型的鲁棒性优化设计方法,多采用CFD计算或代理模型方法进行气动力预测。为了降低计算代价、保证预测精度,本文采用卷积神经网络模型进行气动力的预测。搭建基于卷积神经网络的气动力预测模型;采用多项式混沌方法进行不确定度量化,构建翼型鲁棒性优化设计系统;以RAE2822翼型为基准翼型进行优化设计,对翼型鲁棒性设计方法的可行性进行验证。
1 基于卷积神经网络模型的气动力建模
卷 积神经 网络(Convolutional Neural Net⁃work,简称CNN)模型作为一种基于数据的建模方法[18],不考虑复杂的物理机理,将气动力建模问题看做“黑箱”问题,直接建立气动力与飞行状态之间的关系式。在基于数据驱动的气动力模型建模研究方面,目前多采用浅层机器学习模型,如BP神经网络模型[19]、RBF神经网络模型[20]、支持向量机模型[21]等。相较于这些浅层模型,卷积神经网络模型在训练过程中采用了局部连接和权值共享的方式,减少了权值的数量,使网络易于优化;同时降低了模型的复杂度,减少了过拟合的风险[22]。
在翼型鲁棒性优化设计问题中,不仅需要在特定设计点处(马赫数和攻角视为定值)预测翼型的升力系数,还需要在针对马赫数和攻角的不确定度量化时,预测翼型在马赫数和攻角在一定变化范围内的阻力系数。本文针对上述升力系数和阻力系数的不同预测需求分别建立两个不同的CNN预测模型。升力系数的CNN预测模型的输入参数仅包括描述翼型的16个CST参数,而阻力系数的CNN预测模型的输入参数还需要包括马赫数和攻角。两个CNN模型中均包含两次卷积操作和一次池化操作。两个CNN模型的具体参数和结构如图1所示。
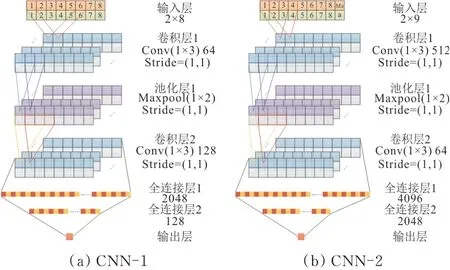
图1 本文设计的CNN结构图Fig.1 CNN structure diagram designed in this paper
基于CNN的气动力建模的样本生成过程为:在样本空间内应用拉丁超立方采样法(Latin Hy⁃percube Sampling,简称LHS)生成一定数量的翼型;应用求解器对生成的翼型进行气动力分析,湍流模型选用RANS模型,计算其升力、阻力系数,生成训练卷积神经网络所需的样本库。
搭建的两个CNN模型的设计状态为:马赫数Ma=0.734,攻角α=2.79°,基准翼型为RAE2822翼型。在样本空间构造方面:以上述马赫数、攻角及基准翼型的16个CST参数为中心,各取一个小的变化区间,形成一个整体的样本空间,其中翼型CST参数的变化区间为基准翼型各个参数的±0.05,马赫数的变化区间为[0.72,0.75],攻角的变化区间为[2.7,2.9]。
两个CNN模型由于输入参数和模型结构方面有所区别,因此训练样本量、训练迭代次数等参数并不相同。本文选用的预测评价指标为均方根误差(Root Mean Square Error,简称RMSE)和平均相对误差(Mean Relative Error,简称MRE),如式(1)所示。两个CNN模型的训练参数和训练结果如表1所示。

式中:n为样本的个数;yi为第i个样本的CFD计算结果;pi为其对应的CNN模型预测值。
两个CNN模型的训练结果如图2所示。从表1和图2可以看出:CNN模型在气动力建模方面的精确度可以满足翼型设计优化的计算要求。
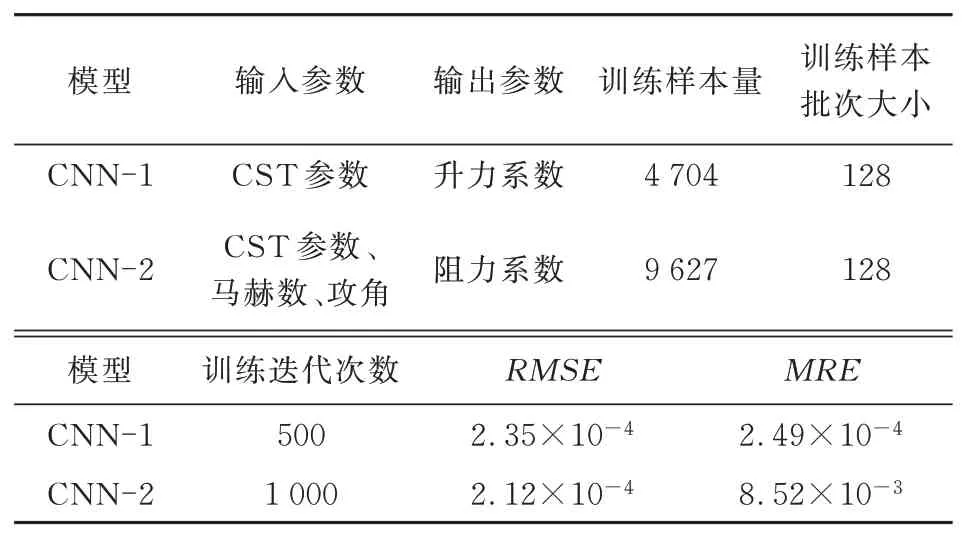
表1 两个CNN模型的训练参数和训练结果Table 1 Training parameters and training results of two CNN models

图2 CNN的气动力系数预测结果Fig.2 CNN’s aerodynamic coefficient prediction results
2 基于多项式混沌方法的不确定度量化
在不确定度量化方面,常用的蒙特卡洛(Mon⁃te Carlo,简称MC)方法因其构造简单而被广泛应用,为了满足计算精度要求,MC方法通常需要大量的样本点,导致计算量大,收敛速度慢[23]。
对比MC方法,多项式混沌(Polynomial Cha⁃os,简称PC)方法在不确定度量化方面具有更高的计算效率[24]。在该方法中,整个数值模拟的过程被认为是随机的,首先针对输入样本选择正交基函数,然后将输出在基函数空间中展开,最后得到输出在基函数谱空间中的完全展开,进而获得各种统计特性,例如均值、均方根值和输入变量的全局敏感度指标等。
本文采用非嵌入式多项式混沌(Non-intrusive Polynomial Chaos,简称NIPC)方法[25-26]进行不确定度量化。通过确定性的气动力模型,例如CFD计算或前文设计的CNN模型,得到采样点{ξ1,ξ2,…,ξN}对应的响应值{y1,y2,…,yN}。往往采样点的数量不小于PC展开中的自由度个数,因此方程组Ψα=Y是一个矛盾方程组[27],其中Ψ作为测量矩阵,Ψij=ψj(ξi)。采用最小二乘法对上述矛盾方程组进行求解。
采样点的数目N跟PC展开中的自由度个数有关,即:
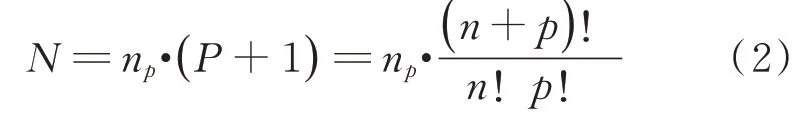
式中:n为输入随机变量的个数;p为混沌多项式的阶数;np为过采样率,根据H.Serhat等[28]的研究,np=2时PC展开的效果较好,因此本文选择np=2。
对输出进行PC展开之后,输出的均值μ、方差σ2等统计信息可直接根据基函数的正交特性得到,即按式(3)进行计算,然后将其应用于鲁棒性优化系统中。
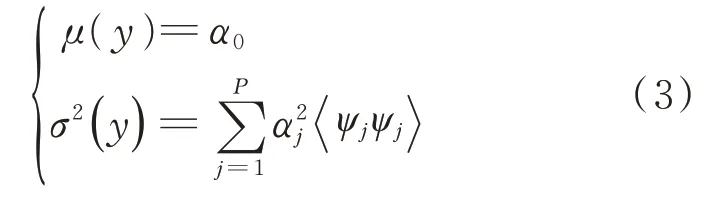
采用NIPC方法研究马赫数、攻角的不确定度对RAE2822翼型阻力系数的影响,假设马赫数、攻角分别满足在区间[0.72,0.75]、[2.7,2.9]上的均匀分布,且雷诺数Re=6.5×106。本算例采用的气动力预测模型为上文提到的CNN-2模型,该模型的精度满足使用要求。
采用蒙特卡洛方法来对比验证NIPC方法的计算精度是否达到要求,使用样本数量为105个,此时响应量的期望概率水平达到10-3,可以达到对比验证的要求。RAE2822翼型的阻力系数均值和方差随着样本点数目变化的收敛情况对比如表2所示。
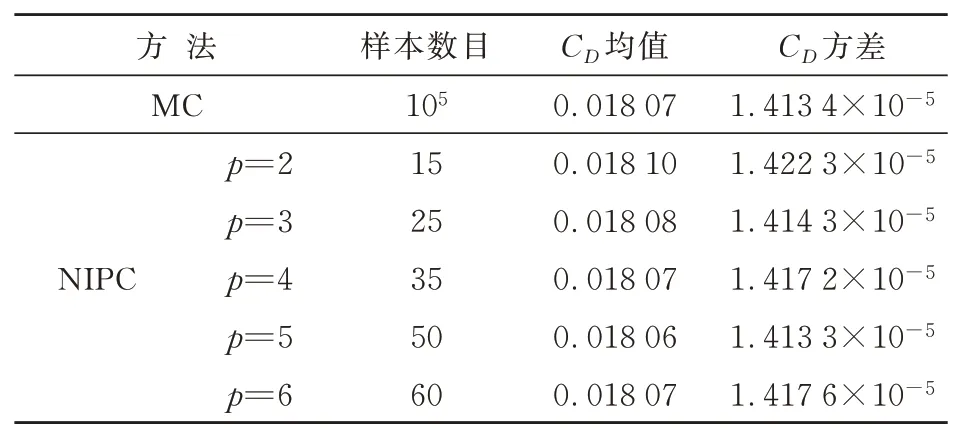
表2 NIPC方法与MC方法的对比Table 2 Comparison of NIPC method and MC method
从表2可以看出:NIPC方法的阶数达到3阶时即可满足使用要求;NIPC方法在样本数量大幅减少至25左右时仍能达到较高的不确定度量化精度,具有高效性和有效性。因此针对RAE2822翼型鲁棒性优化设计中,采用样本数目为25的3阶NIPC方法来完成不确定度量化中阻力系数的均值和方差计算。
3 鲁棒性优化设计系统
3.1 鲁棒性优化设计系统的搭建
本文构建以RAE2822翼型为初始翼型的鲁棒性优化设计系统,该系统采用CNN模型作为气动力预测模型,使用NIPC方法进行不确定性量化,优化算法选择NSGA-Ⅱ[29]进行迭代优化。鲁棒性气动优化设计流程如图3所示。
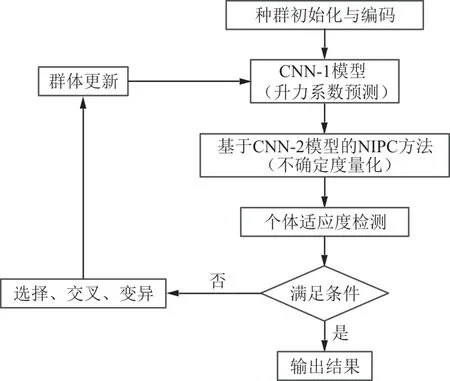
图3 翼型鲁棒性气动优化设计流程Fig.3 Aerofoil robust aerodynamic optimization design process
具体步骤如下:
(1)采用拉丁超立方采样法生成遗传算法所需种群,并对其进行编码和初始化;
(2)调用生成的CNN-1模型对每一个个体进行升力系数预测;
(3)应用NIPC方法进行不确定度量化,确定响应(阻力系数)的均值和方差,其中调用CNN-2模型进行阻力系数预测;
(4)根据遗传算法中设定的约束条件及目标函数计算其适应度,并判断是否满足设计要求;
(5)不满足时则进行交叉、变异、选择过程,并返回步骤(2),直至达到最大迭代次数,迭代结束。
3.2 算例验证
以RAE2822翼型为初始翼型进行翼型的设计优化,设计要求如下:
(1)设计状态:马赫数Ma=0.734,攻角α=2.790,雷诺数Re=6.5×106,其中马赫数和攻角分别满足在区间[0.72,0.75]、[2.7,2.9]上的均匀分布;
(2)优化后翼型的厚度不低于原始翼型厚度的0.98倍;
(3)要求在升力不降低的条件下,降低翼型在设计点的阻力系数,同时保证翼型在不确定变量马赫数和攻角的一定变化范围内,阻力性能的波动尽量小。
将x/c在0.20,0.30,0.40,0.45,0.50,0.55,0.60,0.70,0.80处的厚度不小于原始厚度的0.98倍作为厚度约束,同时还要保证翼型的最大厚度不小于原始翼型的0.98倍。
选择16个CST参数作为优化设计变量,其初值和取值范围如表3所示。翼型鲁棒性设计优化的数学模型为

表3 设计变量初值及取值范围Table 3 Initial value and range of design variables
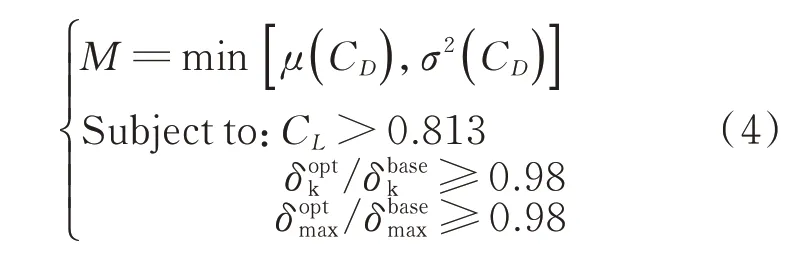
式中:δ为翼型厚度;CL为翼型升力系数;μ和σ2为翼型阻力系数在马赫数和攻角的变化区间内的均值和方差;CD为翼型阻力系数。
NSGA-Ⅱ算法的种群规模为100,最大进化代数为100。
为了进行结果比对,本文还进行相同设计要求下的确定性翼型优化,其数学模型为

该优化过程中使用的气动力预测模型也为CNN模型,优化算法选用经典遗传算法(Simple GA,简称SGA),其相关参数设置如下:种群规模100,交叉概率0.9,变异概率0.1,进化代数100。优化结果如表4所示,优化后的翼型如图4~图5所示。

表4 优化设计结果对比Table 4 Comparison of optimized design results

图4 翼型形状对比Fig.4 Airfoil shape comparison
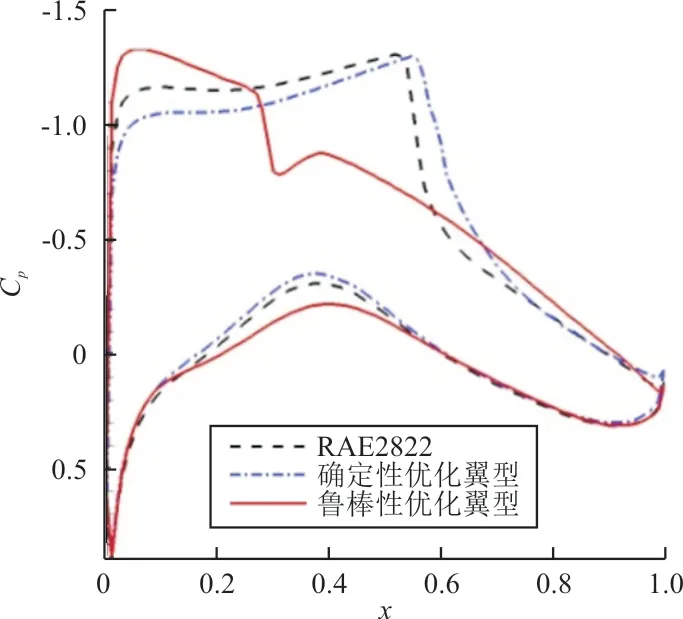
图5 翼型压力分布对比Fig.5 Airfoil pressure distribution comparison
从图4~图5可以看出:鲁棒性优化后的翼型最大厚度后移,激波强度减弱,在升力系数不下降的情况下有效降低了阻力系数,提高了升阻比。
原始翼型和确定性优化得到的翼型阻力发散曲线如图6所示。

图6 翼型阻力发散曲线对比Fig.6 Comparison of airfoil drag divergence curves
从图6可以看出:鲁棒性优化后的翼型在马赫数和攻角的不确定范围内气动特性得到了改善,随着马赫数和攻角的增加,阻力系数变化较为平缓,气动性能较为稳定,达到了鲁棒性优化的目的。
通过该算例的验证分析,体现出本文设计的气动优化方法能够对翼型进行有效的鲁棒性优化,同时该方法相较于其他方法的优势主要体现在优化整体效率的提升。与常规的应用CFD计算作为气动力预测模型的优化流程相比,本文设计的CNN模型虽然在训练样本的准备过程中仍需进行CFD计算,但计算量有所减少。只要设计状态不变,一旦优化算法及相关优化参数(如优化目标函数的构造方式)发生变化,以前训练好的气动力预测模型仍能继续使用而无需再训练,这就提高了整体优化效率。
4 结论
(1)在气动力预测方面,本文设计的卷积神经网络模型满足翼型优化设计要求,预测精度高,可以提高优化设计的整体效率。
(2)在不确定度量化方面,采用的非嵌入式的多项式混沌方法具有明显优势,在样本数量大幅降低的情况下仍能保持计算的准确性,提高了鲁棒性气动优化设计效率。
(3)本文验证了该优化设计方法在RAE2822翼型优化过程中的可行性,其主要策略可望应用于其他翼型的优化设计。

