基于数据驱动的电动自行车换电需求预测

帅春燕，杨芳，欧阳鑫，许庚

(昆明理工大学，交通工程学院，昆明650500)

0 引言

自1995年起，电动自行车在国内的发展趋于成熟稳定，2018年电动自行车的社会保有量达到2.5 亿辆，成为居民短途出行的重要交通工具。随着外卖行业的兴起，电动自行车成为外卖骑手的主要交通工具。为规范电动车的市场和使用，规定电动自行车的最大重量为55 kg[1]，限制了电池的容量，使得单块电池的最远运行距离不超过60 km。因此，产生了电动自行车的充、换电需求，相对充电而言，换电具有耗时短，速度快的优点，能满足突发出行需求。大量的换电企业应运而生，例如，易换电、闪开来电、骑士换电、小绿人、张飞充电、易而充、哈喽换电及电小美等。合理地对换电柜进行选址并准确地预测换电需求是换电企业发展的关键，因此，本文研究四川成都某大型换电企业的换电柜分布，以及换电订单量的变化情况，以划分区域的形式，采用整合移动平均自回归模型，即ARIMA[2]模型预测各区域的换电订单量。对比支持向量回归(SVR)[3]、长短时记忆神经网络(LSTM)[4]、反向传播神经网络(BP)[5]等模型，探讨ARIMA模型在换电需求预测上的适用性，其结果为换电企业合理布局换电柜，投放电池量提供数据支撑。

ARIMA模型由于能够获取时间序列的线性关系和周期关系，被广泛应用于时间序列预测，例如，水文地理、网络流量、客流量、运量、价格、需求、负荷、流感趋势等方面。在研究数据的周期性、季节性方面，XU 等[6]研究道路交通状态变化的周期性，建立ARIMA 模型，较好地预测实时路况。MILENKOVIE等[7]研究高铁月度客流量的季节性，使用SARIMA模型实现准确预测，误差较小。艾欣等[8]使用ARIMA模型根据历史电价预测未来电价，以辅助制定竞价策略。SAHAI 等[9]针对新型冠状病毒COVID_19感染病例数据，建立ARIMA模型，较好地预测COVID_19 的变化趋势。在研究时间序列突变性方面，白丽等[10]研究突发性大客流的特征，提出ARIMA模型与回归模型结合，有效预测短期突变客流。

1 模型介绍

由于现有的换电柜布局不合理，导致换电订单量严重不均衡，大量的换电柜使用率低。为优化换电柜布局，本文提出采用K-means聚类算法对换电柜进行聚类，在聚类基础上，按区域采用ARIMA模型预测换电需求。

1.1 K-means聚类

K-means聚类是一种无监督式学习，将数据集{x(1),…,x(m)} 划分为k簇：C={C1,…,Ci,…,Ck} 。计算k簇聚类质心{o1,o2,…,ok},oi∈R(n),i=1,…,k的 位置：，其中，x为样本点，有m个。根据欧氏距离计算数据点和质心的距离，再重新归类，采用目标函数：最小化划分类别。分类以后更新簇中的质心位置，重复计算和更新，直到质心位置不变。

1.2 ARIMA模型

构建ARIMA模型前需要进行时间序列平稳性检验以及白噪声检验。通常采用扩展迪基-福勒检验(Augmented Dickey-Fuller Test,ADF)，也称单位根检验和The Ljung-Box检验来检验平稳性和白噪声。只有在满足自协方差平稳条件时，才能使用ARIMA模型。

若{xt,t=0,±1,±2,…} 为零均值平稳序列，其中t为时间点，令εt是均值为0，方差为σ2ε的平稳白噪声，且满足

则称xt是阶数为p,q的自回归移动平均序列，即ARMA(p,q)。φ1,…,φp和θ1,…,θq分别为序列和噪声的系数。AR(p)为自回归模型，p为自回归项数；MA(q)为移动平均模型，q为移动平均项数。当q=0 时，为AR(p)序列；当p=0 时，为MA(q)序列。若对ARMA(p,q)模型作d阶差分，得到ARIMA(p,d,q)，且

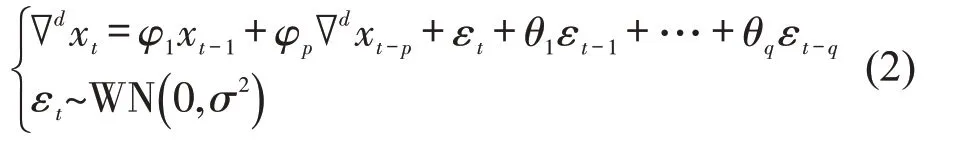
简写为

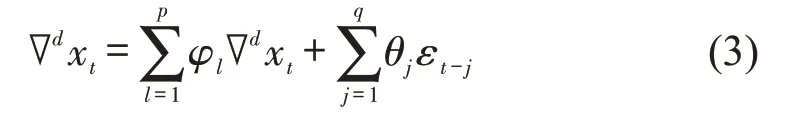
式中：随机序列WN 是独立高斯分布；参数p,d,q通常采用AIC 准则(Akaike Information Criterion)确定。

2 订单预测建模

2.1 数据处理与分析

本文数据采用某大型换电企业在四川成都4个月的电动自行车换电订单量。已有换电柜1252个，对原始换电柜位置进行K-means 聚类，选取800，600，400，200 类作聚类对比，通过4 个类别的订单热力图对比，且考虑到外卖骑手对换电时间、距离的容忍程度，换电站的覆盖面积，选择400类，并在400 类基础上优化得到370 类，每一类视为1个站点。在成都市中心区域的分布如图1所示。

图1(a)、(b)以1000 m 为半径(r)的每个圆形区域包含每个站点的换电柜，在站点密集的区域，通过均衡订单调整重叠区域内的订单到相应区域；图1(c)为聚类前的换电柜热力图分布，分布不均；图1(d)为聚类后，换电柜的数量大大减少，换电柜订单的热力图更均衡，说明单个柜的使用率得到提高，整体的使用率更高，可以降低换电柜的投放量和电池的投放量，从而降低换电企业的成本。

图1 成都市换电站服务区分布Fig.1 Chengdu electrical changing station service area distribution map

将各站点按照平均每小时的订单量(时均订单量)量级划分为大量级(30,60]单·h-1，35个站点；中量级(10,30]单·h-1，106个站点；小量级(0,10]单·h-1，229 个站点，占62%。根据时均订单量，排序得到370个站点的订单分布，如图2所示。

图2 370个站点每小时的平均订单量分布Fig.2 Distribution of average hourly orders at 370 sites

按订单量级的大小，抽取30%的站点(大量级11 个，中量级32 个，小量级69 个)，以1 h 为时间间隔，取连续40 d的数据对订单量进行短时预测。

2.2 模型评价指标

(1)平均绝对百分比误差(MAPE)为

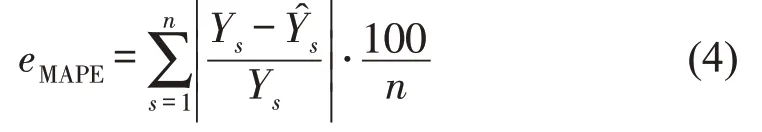
(2)平均绝对误差(MAE)为

(3)均方根误差(RMSE)为

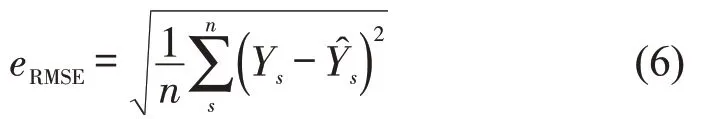
(4)准确率(Accuracy)为

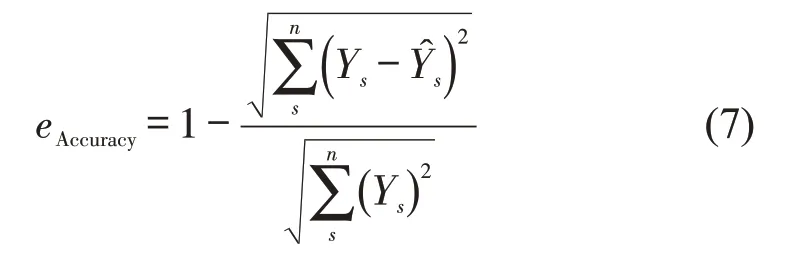
(5)决定系数(R2)为

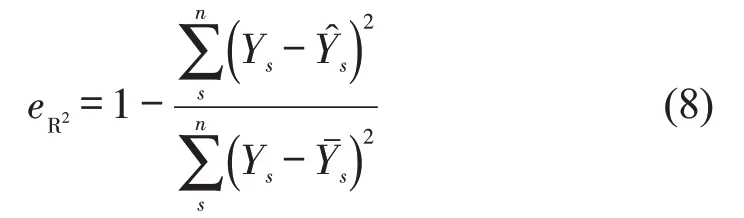
式中：Ys为s时刻对应的换电订单量真实值；为s时刻对应的换电订单量预测值；为s时刻对应的换电订单量真实值的平均值；n为预测的时刻个数。评价指标中eMAPE、eMAE、eRMSE计算模型的误差，eAccuracy、eR2衡量模型预测的精度和拟合度。

2.3 ARIMA时间序列模型

ARIMA时间序列模型建模包括：平稳性检验、白噪声检验以及参数的确定。以23 号站点40 d，960 h的换电订单为例，说明建模过程。

(1)平稳性检验

时序数据的平稳性检验采用ADF检验，如表1所示。

ADF 单位根检验中Test Statistic 为检验统计量，表1中ADF 检验统计量为-2.434819，明显高于3 个显著性水平下的临界值，且P-value 显著大于0.05，说明该序列存在单位根，可以判定23 号站点为不平稳序列，订单时序如图3所示。

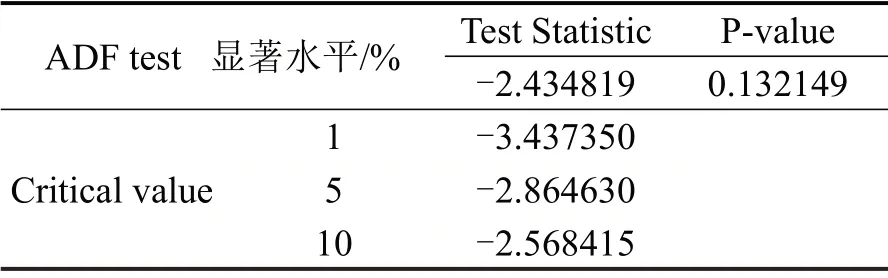
表1 ADF检验结果Table 1 ADF inspection result

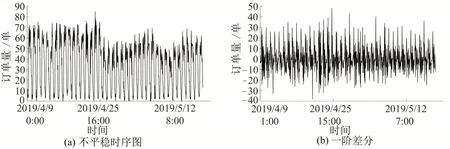
图3 23号站点不平稳时序图及差分图Fig.3 Unsteady timing sequence and difference diagram of No.23 station

观察到换电订单量的时序图无明显趋势性，直接对非平稳序列做差分处理，默认先做一阶差分处理，平稳后不用再次差分。一阶差分结果如表2所示。

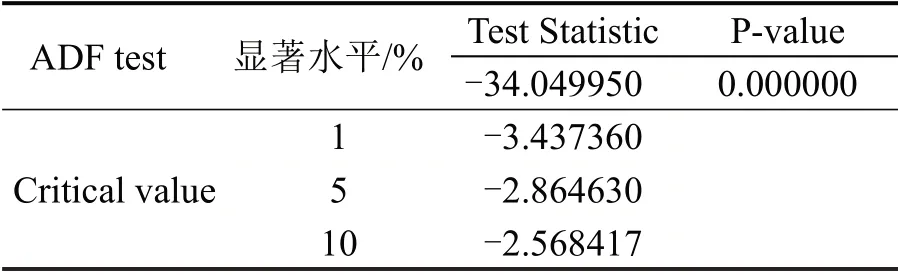
表2 一阶差分ADF检验结果Table 2 ADF test results of first order difference

ADF 统计量为-34.049950，小于1%显著性水平下的临界值-3.437360，单位根不存在，一阶差分结果显示为平稳序列。

(2)白噪声检验

检测序列不是白噪声具有研究意义。差分序列的白噪声检验结果如表3所示。

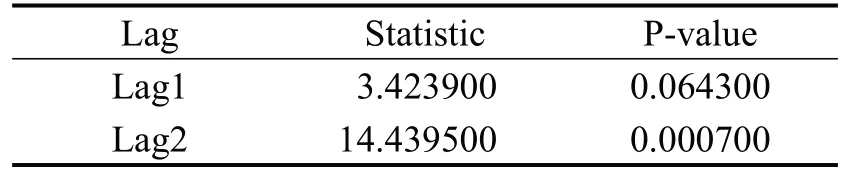
表3 白噪声检验结果Table 3 White noise test results

2阶滞后数以后P-value显著小于0.05，判定为平稳非白噪声序列，可以进行时间序列建模。经过平稳性检验的平稳序列共有30 个站，其中某个站平稳序列时序如图4所示。

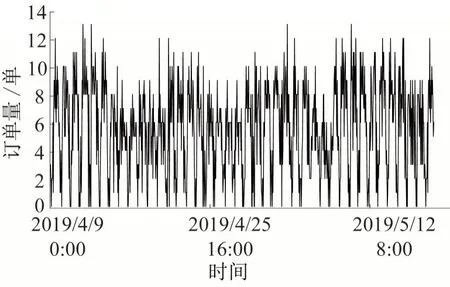
图4 平稳序列时序Fig.4 Stationary sequence diagram

确定模型的p,d,q参数可以通过观察平稳序列的自相关图和偏自相关图进行模型的定阶。由于人为定阶存在误差，无法选择最优阶数，故采用AIC准则自动定阶。

2.4 模型对比

为验证ARIMA模型在短时订单量预测上的有效性，本文选取AR(Autoregressive model)、MA(Moving Average model)、LSTM(Long Short-Term Memory)、SVR(Support Vector Regression)、BP(Back Propagation)神经网络进行实验比较[11]。其中，自回归AR 和滑动平均MA 模型，是ARIMA 的子模型，属于线性模型。支持向量回归SVR 模型通过核函数将低维空间的数据映射到高维空间中，并对支持向量进行回归拟合，实现预测。BP 神经网络通过反向传播误差实现参数寻优。LSTM 是应用于时序预测的深度神经网络，通过多个门进行控制，获取输入数据之间的长、短时时序依赖。为公平起见，上述6个模型均经过了参数寻优。分别对非突变的换电订单数据作预测。模型参数设置如表4所示，各模型模拟结果如图5所示。

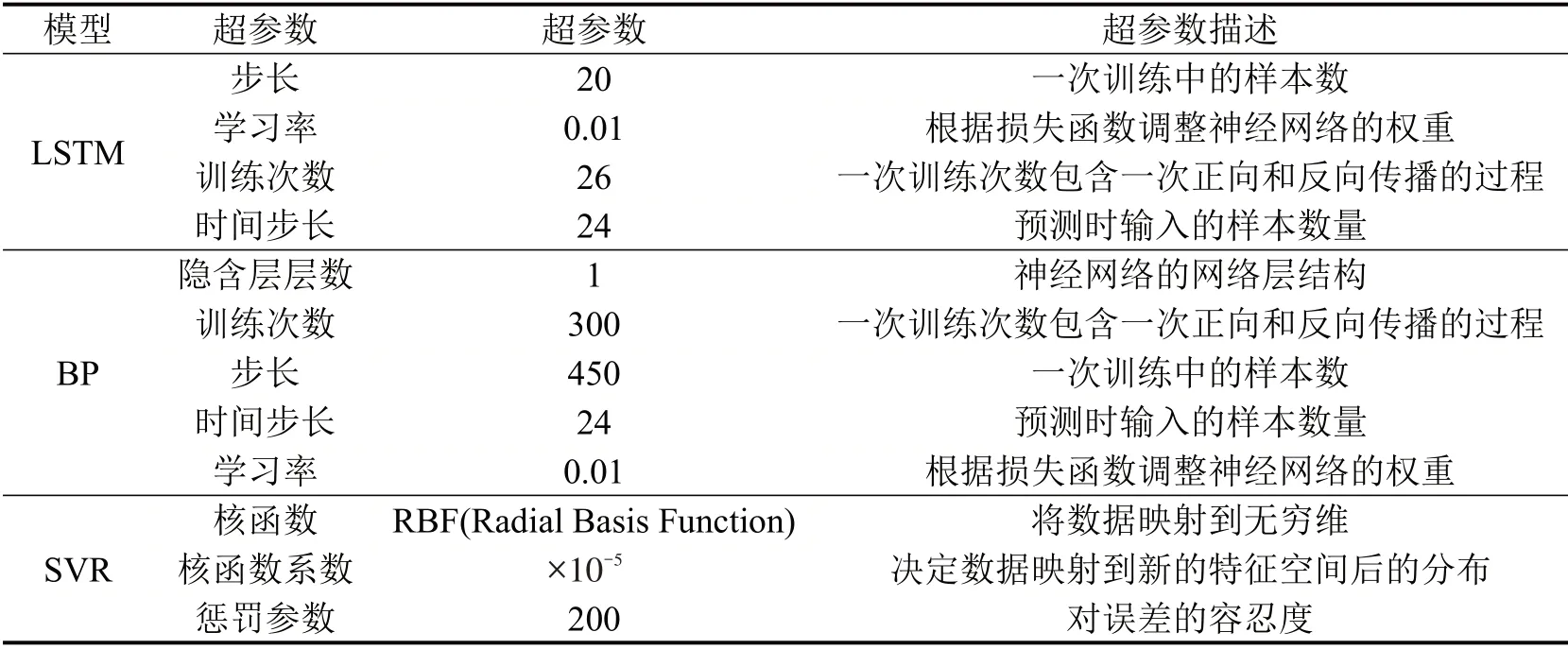
表4 模型超参数Table 4 Model hyperparameter

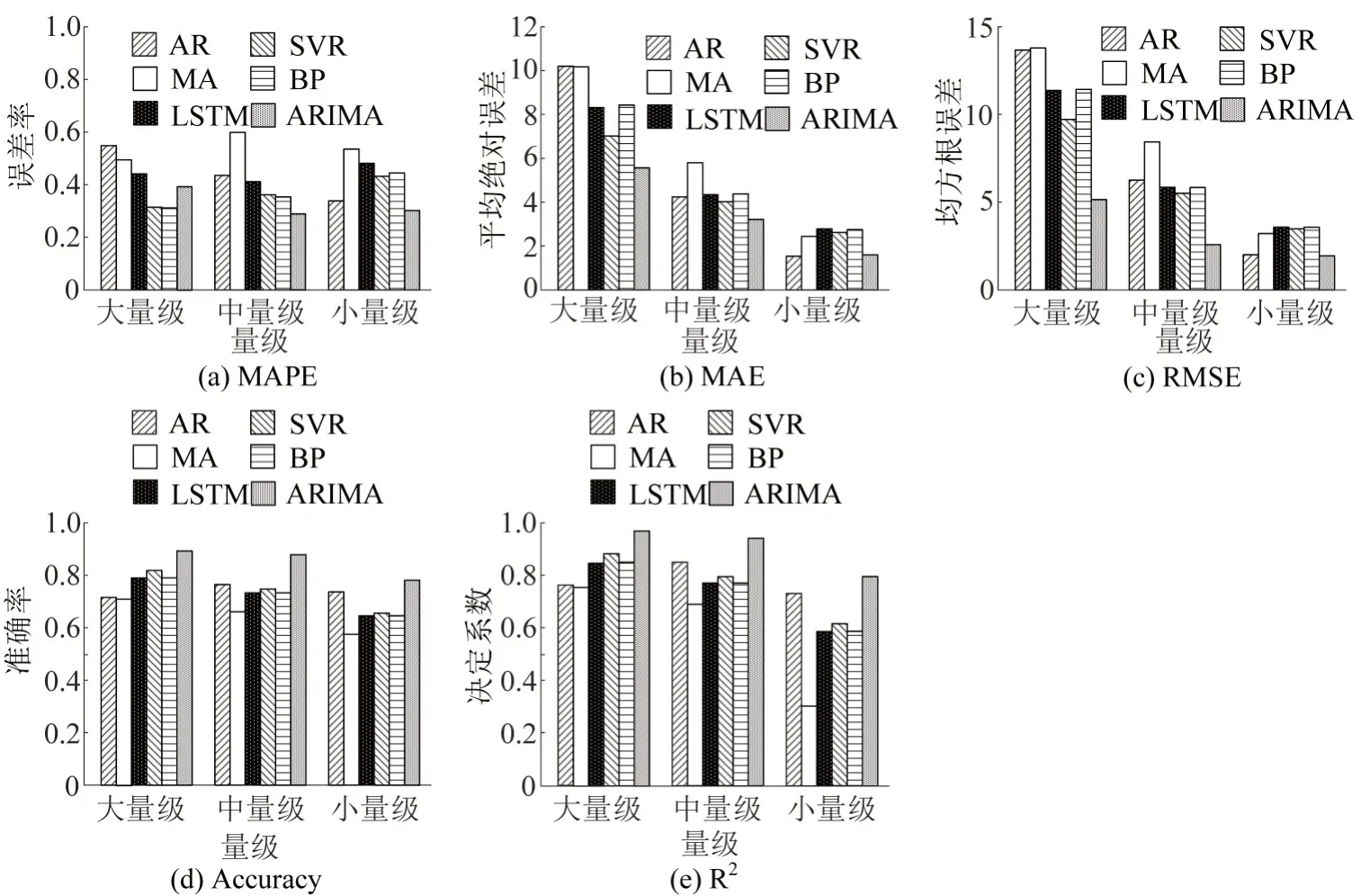
图5 各模型指标汇总Fig.5 Summary diagram of each model index

随着订单量级变小，模型拟合度和精度下降；ARIMA模型在各个量级上的预测效果均优于其他模型。

进一步，比较ARIMA 模型和LSTM、SVR、BP模型在换电柜扩容，导致换电订单量突变，波动较大的情况下的预测性能，对提取出所有订单量突变的71，135，168站点进行实验。其中71号订单突变站点的模型预测如图6所示。

图6中：LSTM、SVR和BP模型预测能力变差，误差增大，ARIMA 模型能够适应突变趋势。这主要是因为ARIMA模型采用前面有限个数据预测后一个数据，适用于周期性和线性特征的数据；而SVR、LSTM 和BP 模型基于所有数据去寻找最优超平面或模型的超参数，故对突变数据敏感，预测性能下降。

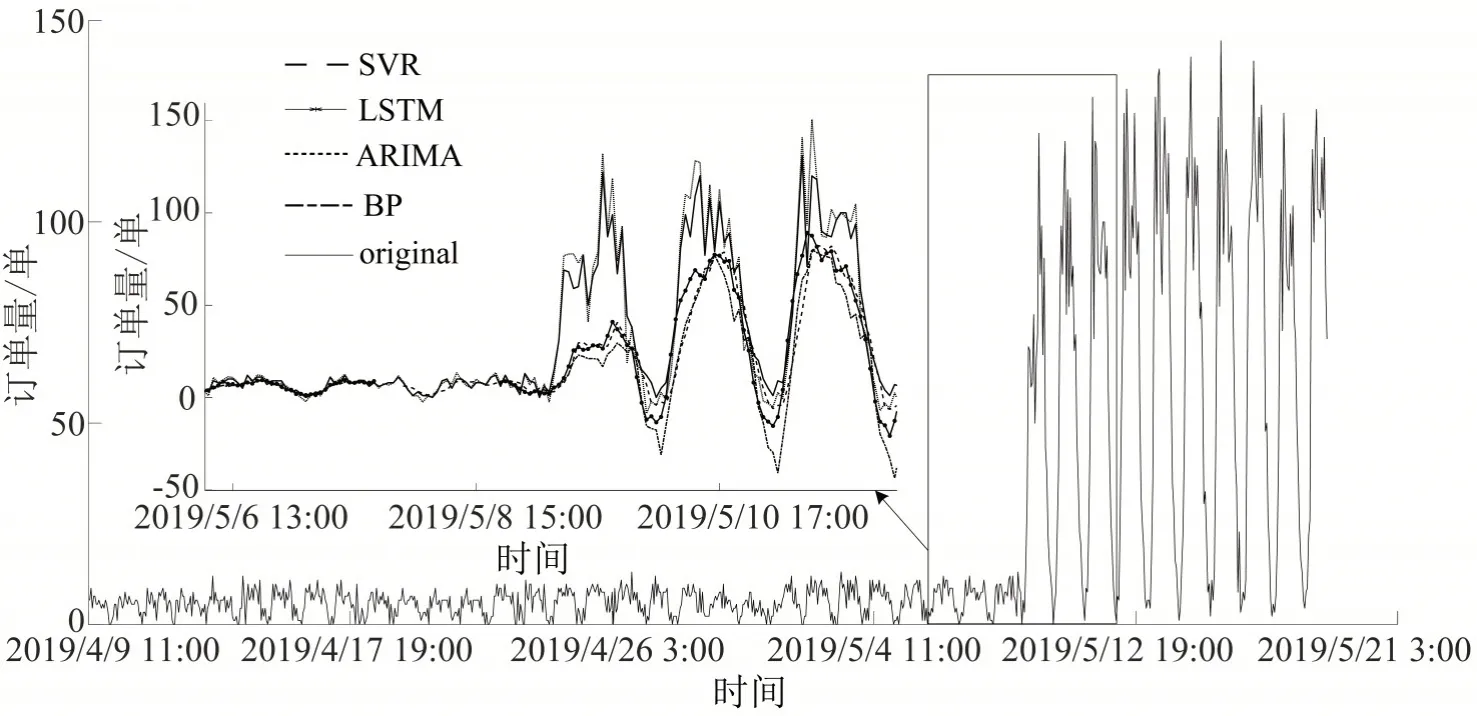
图6 订单突变曲线及4个模型局部预测Fig.6 Order mutation curve and its four model local prediction diagrams

为解决神经网络输入数据需求量较大的问题，并且验证是否因数据量原因导致LSTM、BP 和SVR 模型预测效果差。提取突变订单量数据由40 d扩展到80 d。模型实验结果如表5所示。

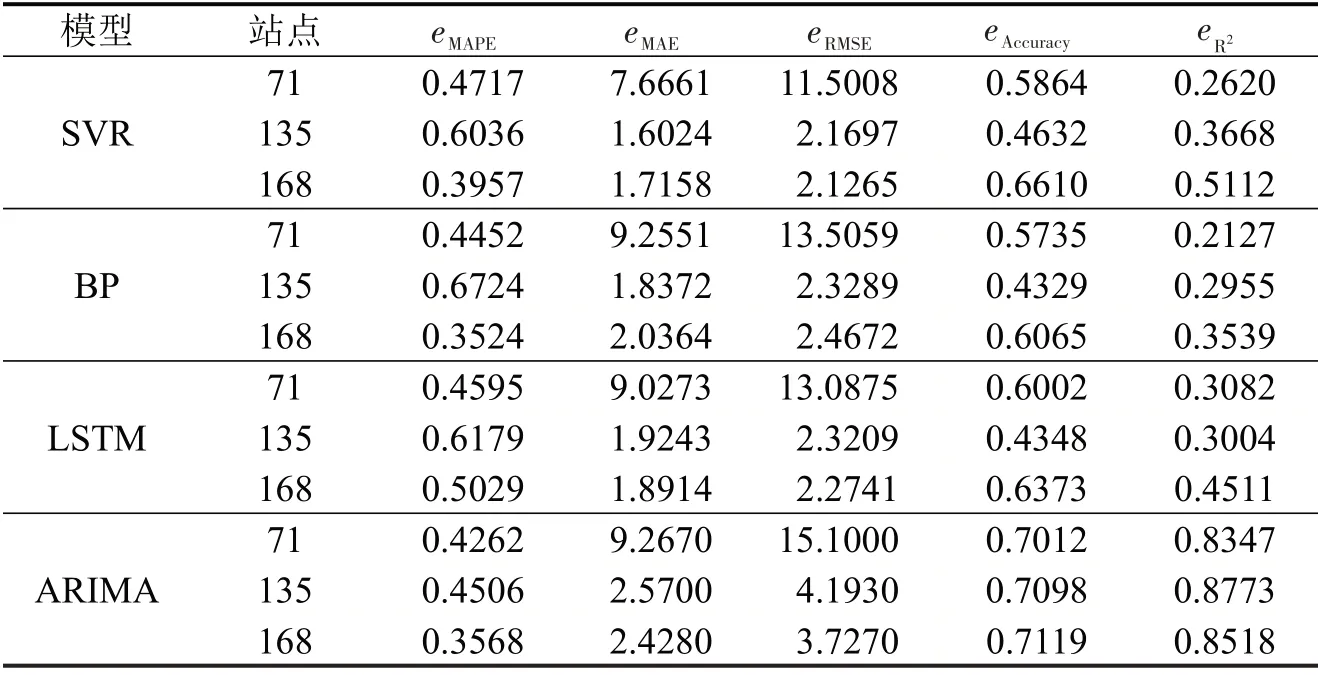
表5 突变订单量实验结果Table 5 Experimental results of mutation orders

面对突变数据，SVR、LSTM、BP模型的预测效果不佳，在扩大数据量之后，依然未能解决预测效果的问题。证明突变数据会影响SVR 模型的最优超平面寻找，LSTM和BP模型因记忆了突变之前数据的权重，以后的每一次预测都会受到突变的影响。

综上，换电订单在时序上具有很强的线性和周期性特征，换电订单量受到短期订单量的影响更大，且短期内的变化具有平稳性，ARIMA模型能够有效地预测换电订单。

预测效果较好的4个模型如图7所示。

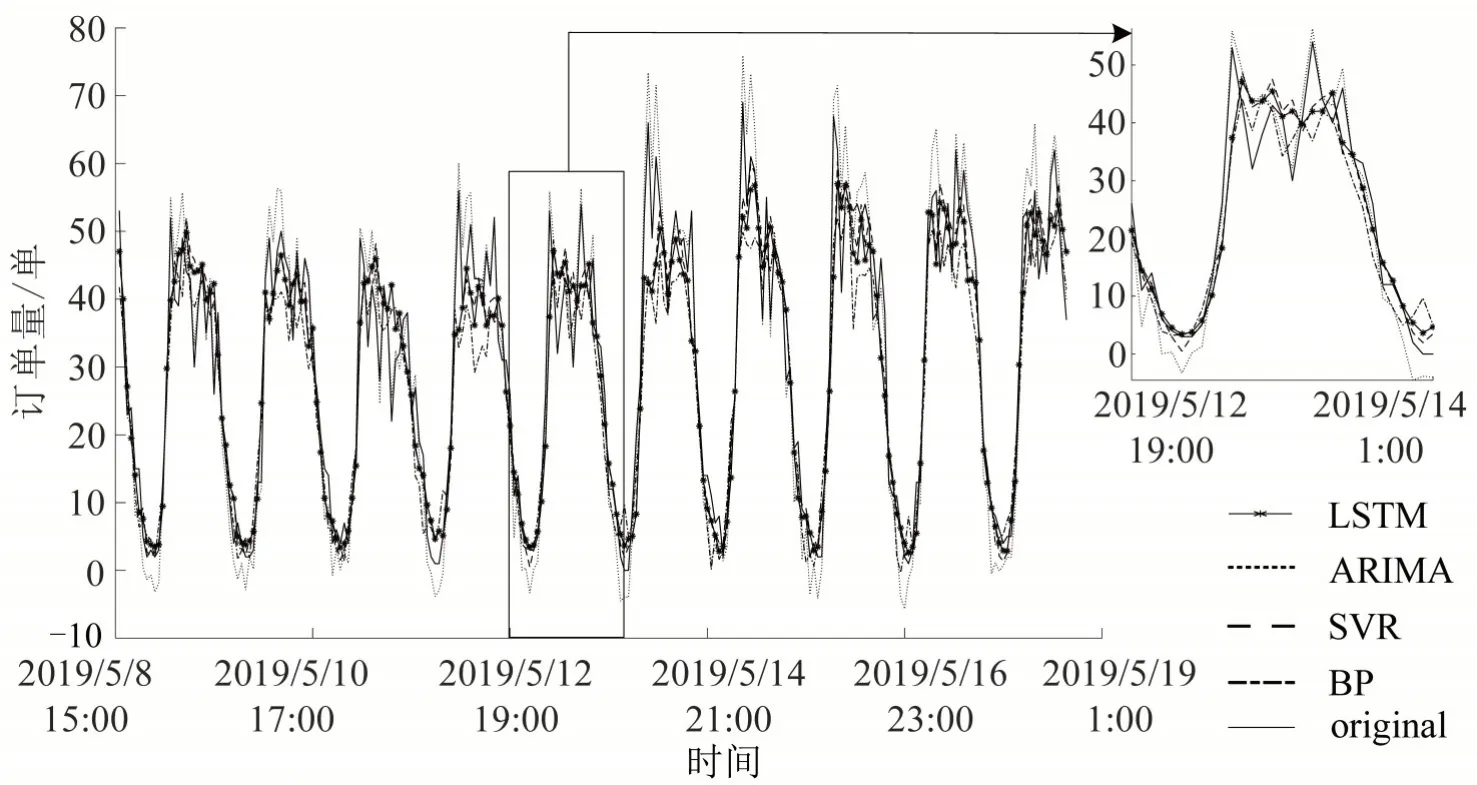
图7 4个模型预测Fig.7 Four model prediction diagrams

ARIMA模型的预测曲线和真实值曲线基本一致，对订单量的峰值比较敏感。进一步，使用ARIMA 模型对余下的70%站点进行拟合预测，结果如表6所示。

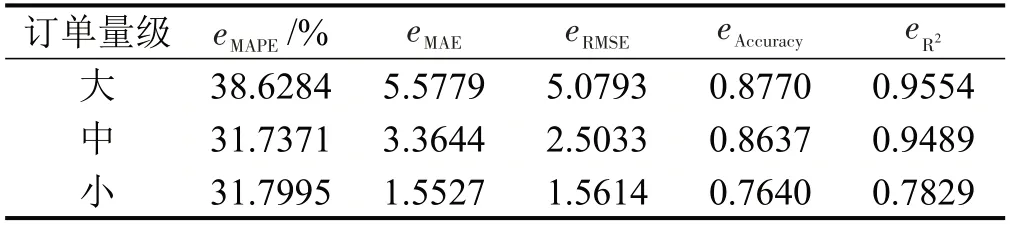
表6 ARIMA模型预测结果汇总Table 6 Summary table of time series ARIMA model results

所有站点的eAccuracy和eR2都在0.75 以上。说明ARIMA模型对换电订单量的预测适配度很好。订单量级变小，模型预测的精度也随之降低。

3 结论

随着电动自行车使用规范的出台，外卖行业的兴盛，换电需求的增大，对换电订单的预测可以优化换电服务，节约换电成本。本文根据换电订单数据的特征，采用K-means 聚类方法聚类数据，提出基于ARIMA 模型的区域换电需求预测，并比较了AR、MA、ARIMA、LSTM、BP、SVR 模型的短时预测性能。发现，订单量量级的大小会影响预测精度，同时，换电量在时序上更多表现为线性和周期性，换电订单量受短期订单量的影响更大，且短期内的变化具有平稳性，这也是ARIMA 模型比其他非线性模型具有更高的预测精度和更低错误的原因。