城市轨道交通地下线车站选址与平面线形优化

汪茜，柏赟*，李佳杰，朱巧珍，冯旭杰

(1.北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京100044；2.交通运输部科学研究院，城市交通与轨道交通研究中心，北京100029)

0 引言

城市轨道交通一旦建成就难以更改，应在建设前进行合理的线路设计，尤其是对客流吸引及线路建设、运营和环境成本均有较大影响的平面设计[1]。目前，轨道交通平面设计方案主要通过人工比选若干可行方案得到，不仅耗时且不能保证结果的最优性。因此，有必要提出一种轨道交通平面设计优化方法，实现车站选址与线路平面自动设计。

轨道交通车站选址优化目标通常包括增大客流吸引和减小线路综合成本。Laporte 等[2]考虑城市轨道交通车站选址方案对线路客流吸引的影响，以车站总覆盖人口数最大为目标优化其布设数量和位置。Repolho等[3]针对高速铁路，以增大客流吸引并减小线路建设、运营总成本为目标优化车站选址方案。然而，此类研究没有对线路平面线形进行设计与优化，只是简单通过直线连接各车站作为最终平面设计方案，没有准确刻画线路综合成本，故无法得到成本最优的轨道交通平面方案。

还有部分学者研究了考虑成本的轨道交通区间线形优化。Li 等[4]针对铁路既有线拆改，提出一种最小化拆改重建费用的区间平面线形设计方法。Ghoreishi 等[5]考虑线路建设、运营和环境等成本优化铁路区间平纵断面线形。然而，上述研究没有考虑车站位置对线路客流吸引与线路成本的影响。为此，Lai[1]等针对城市轨道交通，以线路全生命周期成本最小为目标同时优化车站选址和线路平纵断面线形，但在成本函数刻画中未充分考虑线路综合成本，尤其是环境成本。

综上，轨道交通车站选址方案和线路平面线形均会影响线路综合成本，且车站选址对线路客流吸引有较大影响，两者应协同优化才能在提高客流吸引量的同时降低线路综合成本。因此，本文针对城市轨道交通地下线，以线路客流吸引量最大和包括建设、运营和环境成本在内的综合成本最小为目标建立模型，优化城市轨道交通车站选址方案与平面线形。

1 城市轨道交通平面优化模型

1.1 模型假设

(1)线路起终点站位置固定；

(2)研究区域内人口分布已知，且车站客流吸引量为该站点覆盖的加权人口数；

(3)线路车站从给定备选车站集合中选取。

1.2 决策变量

模型决策变量包括车站选址方案与线路平面线形。其中，选址方案包括车站数量与位置，可用二进制变量集合Z表示，即Z={d(S1),d(S2),…,d(Sk),…,d(SK)}，k与K分别为备选车站集S内车站的序号及总数量，d(SK)=1 表示车站Sk被选中并建设，d(Sk)=0 表示其不被建设。

如图1所示，平面线形可以通过平面直线交点PIS,m的参数来确定[4]，包括其坐标(Xm,Ym)、该点处圆曲线半径Rm及缓和曲线长度Lm。该决策变量可用实数集合U表示，即U={M,Xm,Ym,Rm,Lm} ，m与M分别为平面直线交点的序号及总数量，m∈[1,M]。确定PIS,m的参数后，该点处圆曲线中心Om、夹角α、β、切线长Tm及曲线长度Lc,m的计算参考文献[6]。

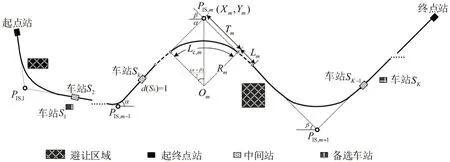
图1 城市轨道交通平面优化模型决策变量示意图Fig.1 Decision variables of optimization model

1.3 目标函数

优化目标为最大化线路客流吸引量P，以及最小化包括建设、运营及环境成本在内的线路综合成本Coverall。此外，为统一各成本数量级，将线路全生命周期内建设Cc与环境成本Ce乘以资本回收系数δ[7]转换为单位年建设与环境成本，再与年运营成本Co累加得到Coverall，即

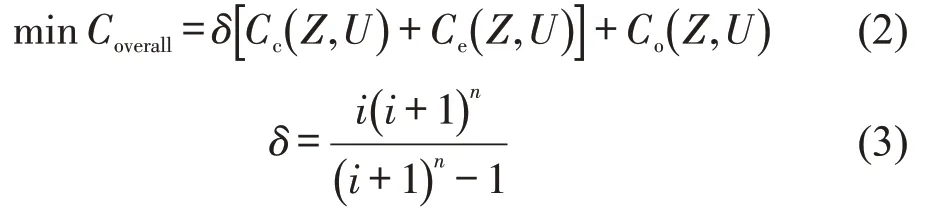
式中：i为年利率(‰)；n为轨道交通运营年限(年)。

1.3.1 客流吸引量

本文假定车站覆盖加权人口数Q作为其客流吸引量。加权人口数计算公式为

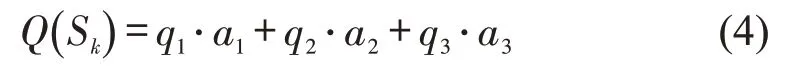
式中：q1,q2,q3分别为距离为(0.0, 0.6] km，(0.6,1.2] km，(1.2，2.0] km 的人口数(万人次)；a1,a2,a3为不同层次区域内乘客选择轨道交通出行的比例，取值分别为0.5，0.4，0.1[2,8]。

首先将乘客来源区按照其位置与地铁站距离远近分为3 个层次[2]，再将每个层次人口数量乘以对应出行比例并累加。线路客流吸引量P可通过累加所有车站加权人口数得到，即

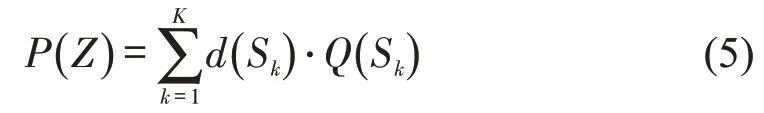
1.3.2 建设成本

针对城市轨道交通地下线拥有独立路权，不考虑拆迁费用，故线路建设成本由车站建设成本Csta和区间建设成本Cline构成，即

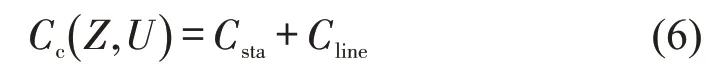
各个车站的建设成本cs(τ)与其规模等级τ有关，本文根据客流吸引量Q的大小将车站划分为3个等级：一级(Q≥1.5 万人次)，二级(0.5 万人次≤Q ＜1.5万人次)，三级(Q＜0.5万人次)[9]。车站总建设成本Csta通过累加沿线所有车站建设成本得到，即

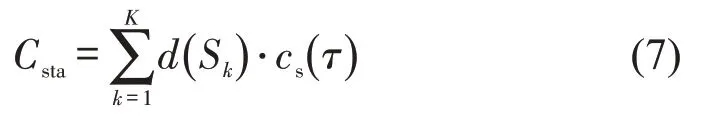
地下线区间建设成本Cline包括隧道建设成本、设备购置与安装成本，以及轨道铺设成本等，均与线路长度L成正比。假定区间单位建设费用为cu，则Cline为

1.3.3 运营成本

城市轨道交通线路的运营成本主要包括车站运营成本Cos、列车运行成本Cot、维修成本Com和轨道交通人员工资Cow，即

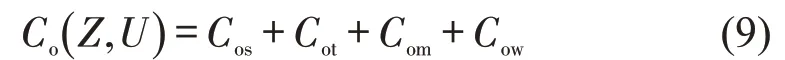
车站运营成本Cos可通过累积沿线所有车站运营成本得到，各车站运营成本co()τ的取值受其规模等级τ影响。列车年运行成本Cot与线路长度L、列车日双向发车次数N及车公里运营能耗E等相关。轨道交通维修成本Com包括基础设施维修成本和曲线部分由轮轨磨损造成的轨道更换成本。其中，基础设施年维修成本约占其总建设成本的1%。而轨道年更换成本可通过曲线长度乘以轨道单位更换成本再除以更换周期(与半径大小有关)得到。轨道交通人员工资Cow与线路长度L成正比。计算方法分别为

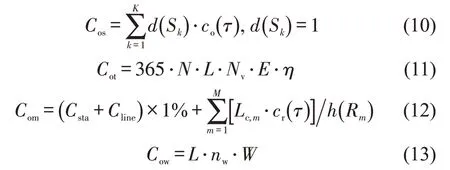
式中：Nv为列车编组数量(节)；η为电费价格(元·(kW·h)-1)；cr为轨道单位更换成本(亿元·km-1)；h(Rm)为曲线半径为Rm时的钢轨更换周期(年)；nw为单位公里下轨道交通工作人员配置数量(人·km-1)；W为轨道交通工作人员年平均工资(万元·年-1)。

1.3.4 环境成本

列车运行过程中会给周边环境带来噪声、振动等不利影响，而不同区域对噪声振动的控制标准不同，故线路经过不同区域造成的单位环境成本存在差异。本文参照《城市区域环境振动标准》(GB 10070-1988)中的规定，将不同区域划分为3个控制等级ω，如表1所示；再将线路分为J段，通过累加各区域线路长度与该区域单位环境成本ce()ω的乘积得到总环境成本Ce，即

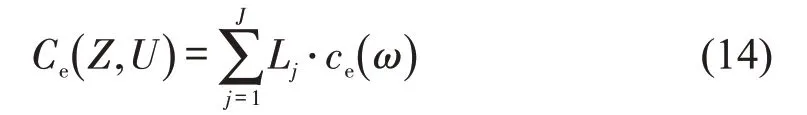
式中：Lj为第j段线路长度(km)。

表1 模型参数设置Table 1 Values of model parameters

1.4 约束条件

城市轨道交通线路在平面设计过程中，其生成方案需满足实际地理条件、站间距、换乘预留及线路平面设计等约束。具体如下。

(1)地理条件

城市轨道交通线路设计通常不能穿越湖泊、文物保护区等避让区域。因此，轨道任意点的坐标(X,Y)与避让区域内的任意点Pr的坐标(XPr,YPr)的直线距离需大于最小间隔ε(本文取值5 m[10])，即

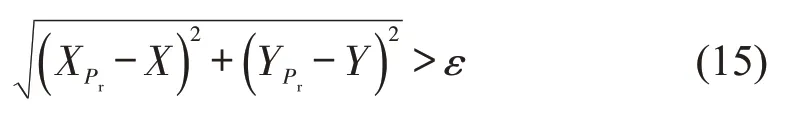
(2)站间距

为避免列车频繁起停或乘客步行到达车站的距离过大，相邻站间距需满足

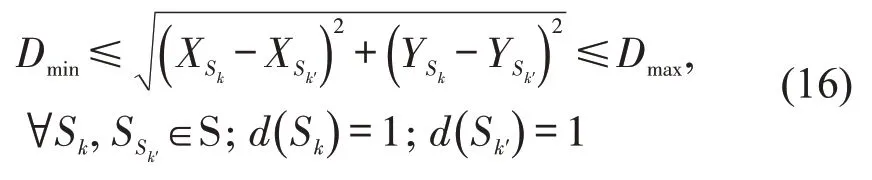
式中：XSk、XSk′表示序号分别为k、k′的车站Sk、Sk′的横坐标；YSk、YSk′为车站Sk、Sk′的纵坐标；Dmin、Dmax分别为线路最小、最大站间距，本文分别取500 m和4000 m[10]。

(3)换乘预留

为发挥轨道交通网络化运营效益，轨道交通车站位置布设需要考虑换乘衔接。因此在线网规划阶段确定的大型换乘站，在车站选址优化过程中不予更改，即

式中：B为线网规划阶段确定的大型换乘站集合。

(4)线路平面设计

出于行车安全需要，《地铁设计规范》指出轨道交通线路的平曲线半径需大于最小值Rmin、线路夹直线长度需大于最小值Ls,min、线路曲线长度需大于最小值Lc,min，以及车站必须设置在直线上。本文取

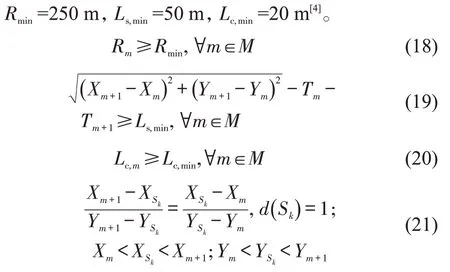
2 求解算法

针对模型约束条件多且非线性的特点，设计混合启发式算法求解。利用带精英策略的非支配排序遗传算法(NSGA-II)求解平面设计方案的帕累托前沿。A*算法(一种在静态路网中求解最短路径的方法)用于在给定车站方案后生成线路综合成本最低的平面线形，得到NSGA-II遗传个体。采用实数编码方式，染色体构成如图2所示，算法流程如图3所示，具体如下。

图2 遗传算法染色体构成Fig.2 Construction of a chromosome of NSGA-II

图3 混合启发式算法流程Fig.3 Process of hybrid heuristic algorithm

Step 1 设置NSGA-II 种群大小Pzq、进化代数G、交叉率Pc、变异率Pm。

Step 2 随机生成Pzq组满足约束的车站选址方案，记录当前代数t=1。

Step 3 利用A*算法搜索给定车站选址方案下的最优平面线形，生成Pzq个遗传个体，形成父代种群Ffa,t。具体过程为：

①将研究区域栅格化，标记出各车站位置；

②以线路综合成本最小为目标，搜索连接起终点和中间车站的最优路径；

③利用最小二乘法对路径进行曲线拟合，得到该组选址方案下的直线交点坐标集[4]；

④在对应的直线交点处随机选取曲线半径和缓和曲线长度，得到Pzq种平面设计方案。

Step 4 计算Ffa,t中个体目标函数值，再进行非支配排序和个体拥挤度计算。

Step 5 根据非支配关系与拥挤度循环选择两个个体参与交叉与变异，生成子代种群Fch,t。

Step 6 将父代种群Ffa,t与子代种群Fch,t混合，再次进行非支配排序和拥挤度计算。

Step 7 根据非支配关系与拥挤度选择Pzq个个体，生成新父代种群Ffa,t+1。

Step 8 依次选择Ffa,t+1中两个个体参与交叉与变异，生成新子代种群Fch,t+1。

Step 9 判断迭代次数是否大于G。若到达，则输出最后一代种群；否则，t=t+1，返回Step 6。

3 案例分析

3.1 实际线路平面方案优化效果

以某城市地铁为研究对象，对其平面方案进行重新规划，以验证本文模型和算法的有效性。线路长度为17.41 km，共设9个地下车站，包括4个换乘站。除该线路原始车站外，本文假定研究区域内道路交叉口、大型商业区及景点附近均可设站，最终确定43 座车站进入备选车站集合，并依次对备选站进行编号。考虑换乘预留，线路起终点站，以及编号为19、26 的换乘车站不进行重新选址优化。模型参数设置如表2所示，算法种群规模200，遗传代数为50代，交叉、变异率分别为0.8、0.01。

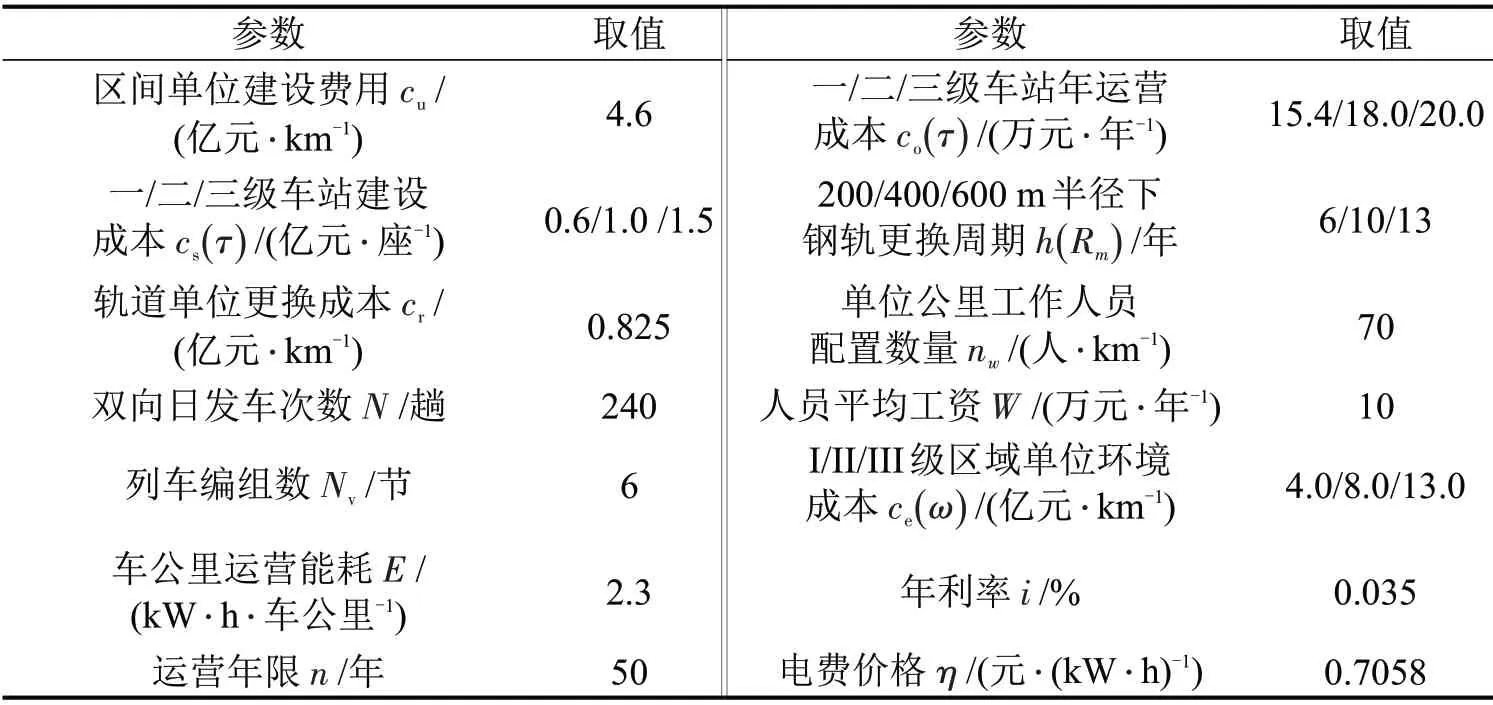
表2 模型参数设置Table 2 Values of model parameters

利用NSGA-II 算法求解模型得到帕累托前沿如图4所示，可以看出，客流吸引量与线路综合成本呈现正相关性。相较于实际平面设计方案，前沿中包含了客流吸引与线路综合成本均更优的解决方案(图4中虚线方框内的方案)。其中，优化方案1可在保证线路客流吸引量不下降的情况下降低约4.4%的线路综合成本，优化方案2可以在保证不增大线路综合成本的情况下，提高线路客流吸引量约9.7%。

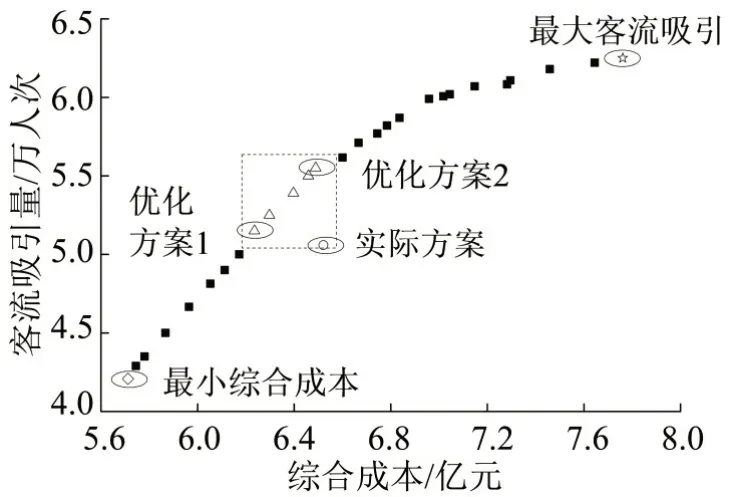
图4 帕累托前沿Fig.4 Pareto frontier of NSGA-II

实际平面方案、帕累托前沿中最小综合成本和最大客流吸引方案的线路走向如图5所示，3 种方案的选址方案及线路成本对比结果如表3、表4所示。其中，最大客流吸引方案相较于实际平面方案增设一座车站，倾向于绕行选择客流吸引量较大的车站建立，使线路客流吸引量增大23.5%的同时线路长度增加了0.9 km，造成线路综合成本上升19.0%。最小综合成本方案相较于实际方案倾向于减小线路绕行距离，使用较短线路连接起终点站，使线路长度减小1.1 km且综合成本下降12.4%，同时其客流吸引量下降16.8%。

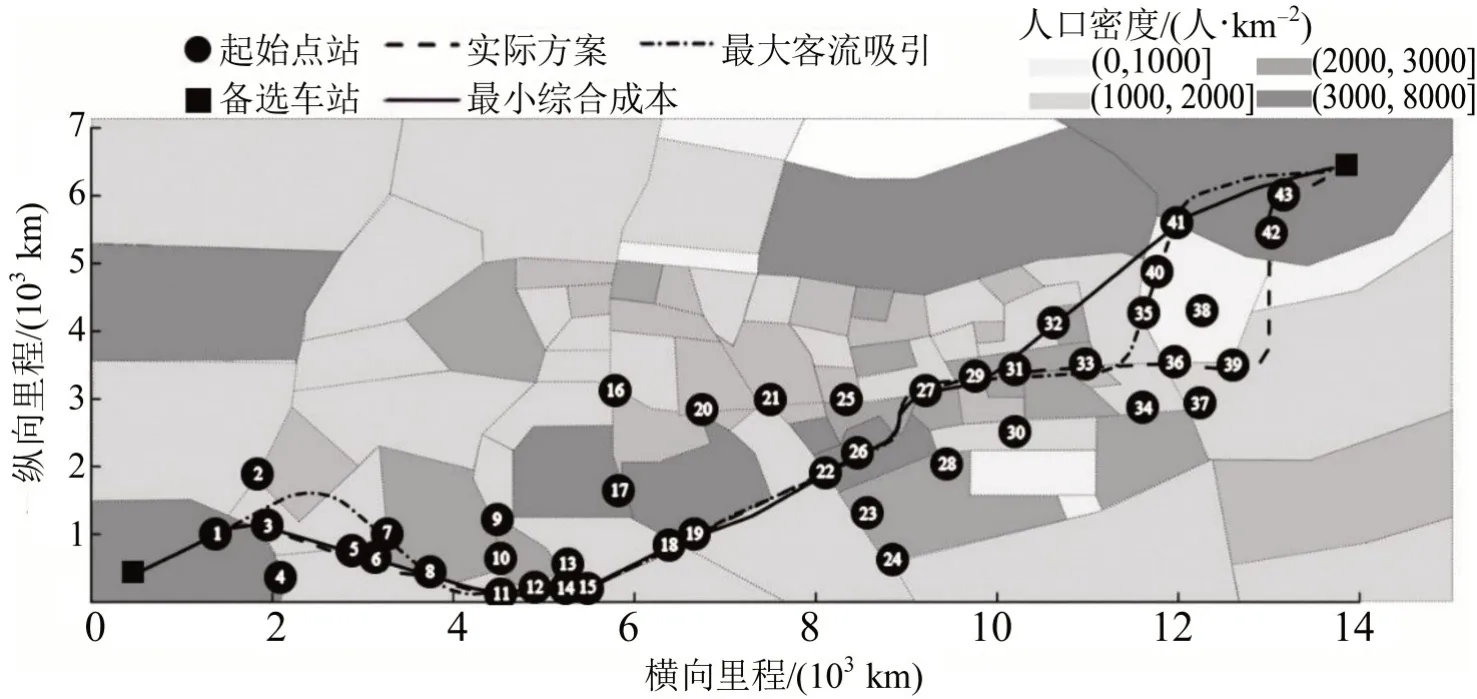
图5 实际线路与优化线路走向对比Fig.5 Comparison between practical alignment and optimized alignments

表3 实际线路与优化后线路车站选址方案对比Table 3 Comparison of station location between practical alignment and optimized alignments

表4 实际线路与优化线路成本对比Table 4 Comparison of costs between practical alignment and optimized alignments

3.2 灵敏度分析

线路平面走向不仅受避让区域位置影响，还受环境成本影响。为分析模型对避让区和环境成本的敏感性，在研究区域内设置避让区域和环境影响区域，如图6所示，重新优化线路平面。在优化过程中不考虑避让区和环境影响区的为优化方案3，仅考虑避让区的为优化方案4，同时考虑两者的为优化方案5。

由图6可知：方案4 与方案5 在优化过程中均考虑了避让区，其线路均成功避开此区域；此外，方案5因考虑了环境影响区，其穿越环境影响区的线路长度相较其他方案更短。从图7中3种方案的线路成本及长度对比可以看出：方案3因不考虑避让区与环境影响区，其绕行距离最短，建设和运营成本最低；方案5 因同时考虑了环境影响区和避让区，其绕行距离最长，但环境影响成本为三者最低。综上，本文模型对避让区与环境影响区有较高的敏感性，可以得到满足施工条件且对周边环境影响较低的平面设计方案。

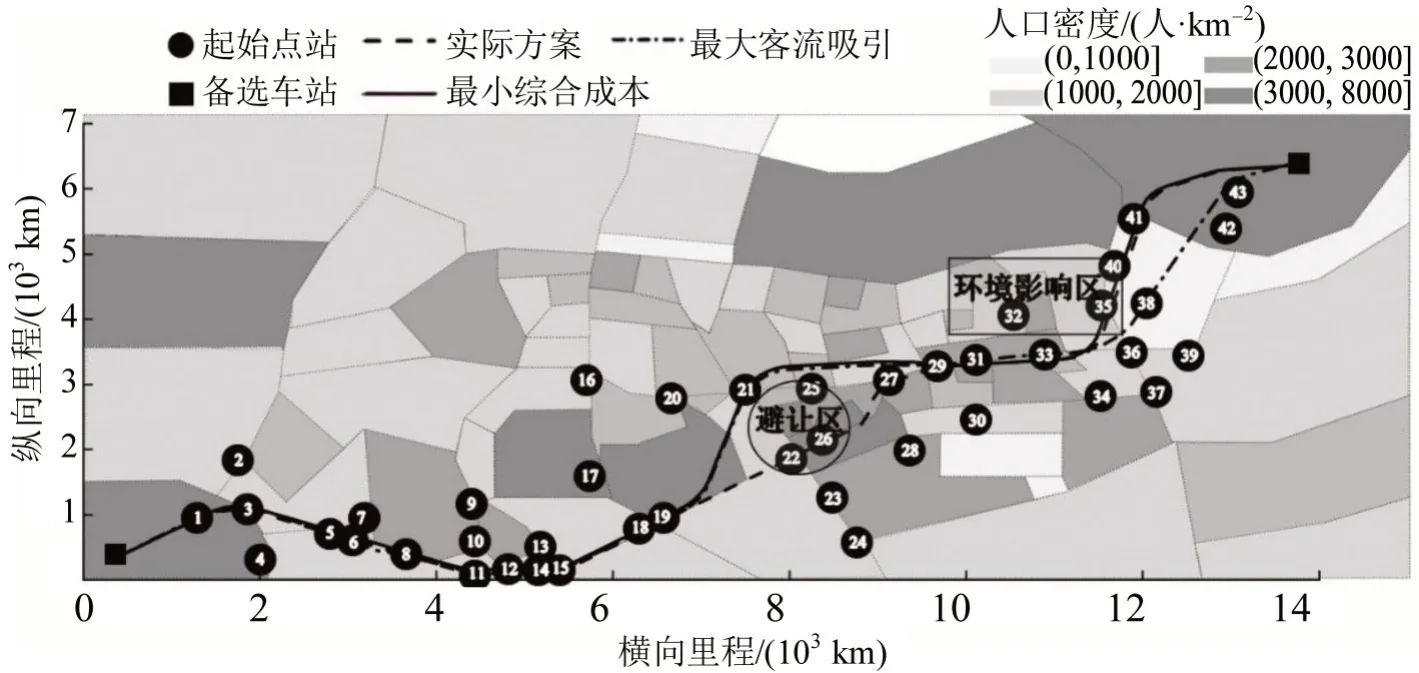
图6 考虑避让区与环境影响区的优化线路对比Fig.6 Comparison between alignments with considering limited area and environmental impact area

4 结论

本文构建了城市轨道交通地下线平面优化模型，设计混合启发式算法求解该模型的帕累托前沿，通过案例验证了模型与算法的有效性。主要研究结论为：客流吸引量与线路综合成本呈现正相关性，且随着客流吸引量的增加，线路长度与综合成本也逐渐增大；相比于经验丰富工程师设计的线路平面设计方案，本文模型优化方案最高可节省12.4%的工程投资、运营和环境等成本支出，同时也可在不降低客流吸引量的情况下减少约4.4%的线路综合成本；模型可充分考虑避让区和环境影响成本，在满足现实设计需要的情况下得到线路综合成本较低的轨道交通平面设计方案。