kc-M模型在凝汽器传热系数变工况计算中的应用

夏立国，石晓玲，熊 辉，邹 春，吴杨辉

（1.国家电投集团江西电力有限公司景德镇发电厂，江西景德镇 333000；2.南昌科晨电力试验研究有限公司，江西 南昌330096）

0 引言

凝汽器是汽轮发电机组最为重要的辅助设备，它的性能将直接影响机组的安全性及经济性[1]。对于高参数的大容量机组，若凝汽器真空降低1 kPa，则汽轮机热耗增加0.6%～1.3%[2]。在凝汽器的运行中，传热系数是确定凝汽器性能的关键参数[3]，在凝汽器设计、运行和技术改造中有重要作用。如何准确快速确定汽轮发电机组凝汽器在变工况下的传热系数一直是工程人员关注的重点之一，不断有研究者对传热系数的确定进行研究[4]。文中将从试验测试的角度出发，通过有限试验数据的分析，获得变工况下现役机组凝汽器传热系数的确定方法。

1 常见凝汽器传热系数确定方法

1.1 试验测试方法

对于实际运行机组，工程上更多是通过试验方法来进行确定凝汽器的实际传热系数[5]。按照《凝汽器性能试验规程》及《汽轮机性能试验规程》的测试要求来测量相关的性能参数，结合式（1）来计算凝汽器总体传热系数实际值kc。

式中：

Dw为循环水流量，kg/s；

tw1为循环水入口水温度，℃；

tw2为循环水出口水温度，℃；

ts为凝汽器压力对应的饱和温度，℃；

Ac为凝汽器换热面积，m2；

cp为循环水定压比热，kJ/（kg·℃）。

试验测试方法必须在机组稳定运行工况进行测试，只能确定有限工况下的传热系数。如果要获得其它变工况下的传热系数，还需要利用经验公式修正。

1.2 经验公式计算法

凝汽器是典型的管式换热器，传热过程分为三个：管外凝结换热过程、管壁导热过程和管内对流换热过程。其单管换热系数可由式（2）确定：

式中：

as为汽侧凝结换热系数，kW/（m2·℃）；

λ为冷却管壁的导热系数，kW/（m·℃）；

aw为水侧对流换热系数，kW/（m2·℃）；

d1为冷却管外径，m；

d2为冷却管内径，m。

但工程中并不能采用式（2）来计算凝汽器的传热系数，因为凝汽器是多根冷却水管的复杂组合，凝汽器的面积、结构、材质以及表面清洁度等都会对传热产生很大的影响。因此实际工程中往往是采用的是经验计算公式计算凝汽器传热系数[6]，如美国传热学会HEI 标准、英国电气机械制造协会标准（BEAMA）、西门子（Siemens）公司计算公式、前苏联别尔曼计算公式等等。其中应用较多的是别尔曼公式（如式（3）所示）和HEI标准（如式（4）所示）[7]。

式中：

φ为凝汽器冷却表面清洁程度修正系数；

φt为冷却水进口温度的修正系数；

φw为冷却水流速和管径的修正系数；

φz为冷却水流程的修正系数；

φd为凝汽器单位面积蒸汽负荷的修正系数；

φM为凝汽器管材和管厚的修正系数。

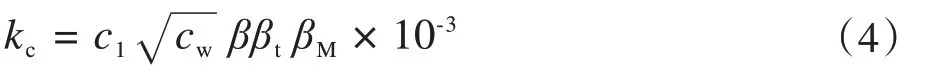
式中：

c1为与外径有关的系数；

cw为冷却水流速，m/s；

钛合金中硅元素曲线会随时间、环境变化，多次分析后产生偏离，如果不进行标准化，则钛合金中硅含量测定结果不准确。在PDA-8000光电发射光谱仪进行了更换增压气水量、维护激发台、清扫聚光透镜、更换泵油、描迹、更换标准化样品、更换氩气钢瓶的工作后均需进行标准化工作，否则测定结果波动很大。标准化分析后，检查内标元素强度值和分析元素标准化校正系数α、β以及κ值，确认与前值无太大变化。钛基体选用Ti323.2 nm作为内标通道，用RTi11/29、BST-5A、BST-81三个标样进行钛合金标准化，确保分析结果准确可靠。

β为冷却管清洁系数；

βt为冷却水进口温度修正系数；

βM为凝汽器管材和壁厚的修正系数。

上述公式中既考虑了冷却管外径、冷却管壁厚、凝汽器管材、传热面积等凝汽器结构方面的影响因素，也考虑了循环水流程数循环水流速、循环水入口温度、冷却管清洁度、蒸汽负荷等凝汽器运行方面的影响因素，可以实现变工况下凝汽器传热系数的计算。但实际工程中，影响传热系数的因素还有很多，如凝汽器入口蒸汽流场分布[8]、凝汽器管内强化传热措施[9]、凝汽器水室结构[10]、凝汽器管束布置[11]、凝汽器管板尺寸[12]等，这些因素上述经验公式均未考虑。而且经验公式的修正系数是已有凝汽器的经验总结，随着机组容量增大，现有经验公式计算得到的传热系数与实际的传热系数的偏差越来越明显[13]。因此，需要寻找更适合实际给定机组的传热系数经验计算公式。

2 凝汽器传热系数kc-M模型

2.1 工况标定参数M的确定

对于凝汽器结构确定的汽轮发电机组，正常运行时传热系数kc与循环水流量Dw、循环水入口水温度tw1、循环水出口水温度tw2、循环水的定压比热cp、凝汽器压力pc对应的饱和温度ts等5个参数相关。在机组负荷pe、循环水流量Dw和循环水入口水温度tw1确定的情况下，正常运行机组的凝汽器工作压力pc确定，其对应的饱和温度ts也确定。而且此时汽轮机排汽流量Dc、排汽焓hc和凝结水焓h'c也是确定的，则根据凝汽器热平衡方程（式（5））可知，循环水出口水温度tw2确定。因此在机组负荷Pe、循环水流量Dw和循环水入口水温度tw1确定的情况下，正常运行机组的传热系数kc是Pe、Dw、tw1和cp四个参数确定，如式（6）所示。

表1列出了Pe、Dw、tw1和cp四个参数的量纲表达式，涉及的基本量纲有4个，分别为长度L、质量M、时间T和温度Θ。

表1 四个参数（Pe，Dw，tw1，cp）的量纲表达式

分析表1 中四个参数的物理量纲，可以发现当量纲指数a为1 时，这四个参数可以组成一个无量纲参数M，如式（7）所示。

由于水的定压比热可视为常数，因此定义无量纲数M是由循环水流量、循环水入口水温、机组负荷这三个参数确定的工况标定参数。

2.2 kc-M模型的建立

在300 MW 亚临界机组仿真机上模拟不同工况下凝汽器正常运行时的传热特性，传热系数根据式（1）确定，工况标定参数M根据式（7）确定。图1 给出了传热系数kc随M变化的情况。

图1 传热系数kc随M变化的仿真模拟

从图1 中可以看出，传热系数kc随M的增加而减小，曲线拟合时，幂函数的误差最小。而且循环水流量不同时，幂函数曲线亦有所差异。这表明，无量纲参数M足以在循环水入口水温、机组负荷与传热系数kc之间建立幂函数关系，而循环水流量的影响还需要通过对幂函数系数的修正进一步完善。因此可建立kc-M模型，如式（8）所示。

式中a、b为仅与循环水流量相关的系数，而M 取决于循环水入口水温、机组负荷和循环水流量三个因素。

3 kc-M模型的应用

国内某330 MW机组的凝汽器型号为N-16 300-1，双流程设置，冷却面积为16 300 m2，冷却管规格为Φ25×1 铜管，冷却管根数为21 400 根，循环冷却水量有两种。按照相关试验规程要求，得到该机组不同工况下凝汽器正常运行数据如表2 所示。根据式（4）计算凝汽器总传热系数kc，然后结合试验数据将Pe、Dw、tw1带入公式（7）中计算M，结果亦列入表2。

表2 凝汽器运行试验数据及kc、M计算结果

表3 幂函数拟合试验数据

表3 中幂函数的系数a和b与循环水流量相关，在两种流量下采用线性拟合，可得a和b的计算公式如式（9）。

则该机组的kc-M模型如式（10）所示。

应用别尔曼公式和HEI 公式计算该机组上述工况下的传热系数，并与试验值和kc-M 模型计算值比较，如图2所示。

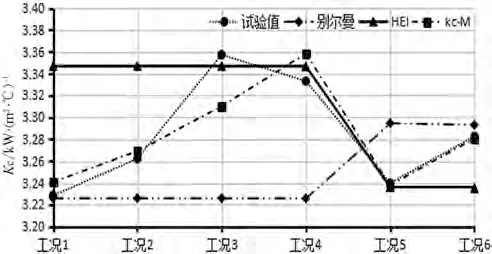
图2 凝汽器传热系数计算值与试验值的比较

由图2 可知，三个公式（式（3）、式（4）和式（10））的传热系数计算值都比较接近试验值。图3 给出了三个公式与试验值相比的误差，由图可知，别尔曼公式和HEI 公式在不同工况的计算误差最大均超过3.5%，平均误差超过1.4%，而kc-M模型计算误差最大为1.41%，平均误差为0.5%。

图3 凝汽器传热系数计算误差

4 结语

1）基于量纲分析得到凝汽器工况标定参数M，通过仿真机模拟研究发现，凝汽器变工况时，凝汽器传热系数kc与M之间为幂函数关系，从而建立了考虑循环水流量、循环水入口水温、机组负荷的凝汽器传热系数变工况计算模型。

2）针对某实际现役机组，建立kc-M 模型，计算不同工况下的凝汽器传热系数。与别尔曼公式和HEI 公式的计算结果相比，kc-M 模型的计算误差更小。