旋流器固-液分离的数值模拟
喻九阳,孟观林,彭 康,汪 威,张思奥,林 纬,徐建民,王家全
武汉工程大学湖北省绿色化工装备工程技术中心,湖北 武汉 430205
水力旋流器因分离高效、操作简单和价格低廉等优势,而被石油、环保、污水处理等领域所青睐[1-2]。水力旋流器虽然结构简单,但其结构尺寸、入口流量、砂粒浓度改变会对分离效率有很大影响[3-4],这些因素影响水力旋流器内的湍流和砂粒之间的相互作用,进而严重影响设备的工作效率。水力旋流器在不同工况下能耗和分离效率不同,导致旋流器在面对复杂工况时,难以高效运行,因此设计和制造高效率旋流器对降低工业成本具有重要意义。许多学者对旋流器影响因素进行了大量研究,黄帅彪[5]对水力旋流器分离性能进行了实验研究,结果表明,旋流器结构对固-液分离效能有很大影响。陈柯杰等[6]采用EDEMFLUENT 耦合数值仿真分析方法,提出了颗粒入口位置分离效率的新概念,利用这一概念确定水力旋流器的总分离效率。王建等[7]通过等比例缩小旋流器模型,试验研究了不同操作工况与分离效率的关系。吴允苗等[8]研究表明了倒锥结构具有促进分离效果的作用。崔之健[9]采用Mixture多相流模型对三相旋流器进行耦合分析,确定了结构优化后旋流器的最佳进口流量区间。刘华冰等[10]利用CFD 软件对固-液微型旋流器进行研究,得到了内部压力场和砂粒分布等规律。以上学者并未对工业级旋流器进行细致研究,且实验方法耗费大量人力物力,需要很多配套设施,而数值模拟相对容易进行,操作方便。本文采用数值计算方法对固-液旋流器进行研究,得到了旋流器的最优工况,为工业上应用水力旋流器提供了数据支撑。
1 模型及方法
1.1 几何模型及网格划分
根据里特马关系式[11],由式(1)确定旋流器的圆柱段直径。
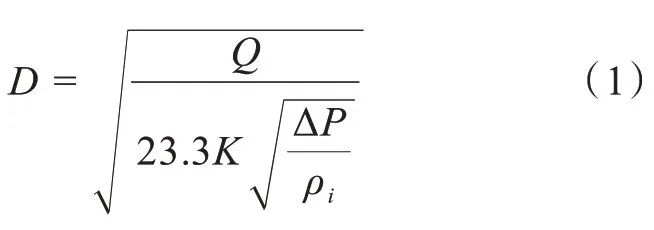
式中,D为旋流器圆柱段直径,m;Q为入口流量(进料量),L/s;ΔP为压强降,Pa;ρi为悬浮液的密度,kg/m3;系数K。
取 ΔP=0.340 MPa,ρ砂=3 000 kg/m3,ρ水=998 kg/m3,K=1.3,入口流量Q=10 m3/h=2.78 L/s。假设悬浮液浓度为泥砂浓度10%,则悬浮液密度ρi=0.9×998+0.1×3 000=1 198.2 kg/m3,由式(1)可得D=74 mm,取标准圆筒直径D=75 mm。根据JB/T 9035-2015《水力旋流器》标准[12],确定旋流器各结构尺寸:当量直径de=0.25D=18.75 mm,圆整取de=19 mm,即当量面积A=3.14(de)2/4=283.4 mm2;标准矩形入口尺寸为a=2b,则a=24 mm,b=12 mm;d1=0.3D=22.5 mm,圆整取d1=22 mm;d2=0.1D=7.5 mm,圆整取d2=8 mm;h1=1.4D=105 mm;h2=0.3D=24 mm;厚度S1=5 mm;取θ=15°。
选用的旋流器为单切向入口,旋流器主体由进料口、溢流口、底流口、圆柱段和锥段组成。固-液混合液从旋流器的进料口进入旋流器内;由于颗粒在旋流器中受径向离心力不同,细小颗粒主要在旋流器内轴线附近做回转运动,并由溢流口流出形成溢流;较大颗粒则在旋流器靠近器壁处做旋转运动,从底流口流出形成底流;固-液分离主要发生圆柱段和锥段。为了对旋流器内部流场进行分析,选取Y1-Y66 个截面为旋流器的研究界面,如图1(a)所示。根据旋流器的结构特点,本文用六面体结构网格划分,如图1(b)所示。
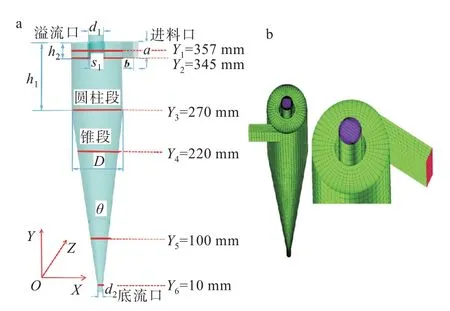
图1 旋流器几何模型示意图:(a)截面选取,(b)网格划分Fig.1 Schematic diagrams of geometric model of cyclone:(a)corss section,(b)mesh generation
1.2 数值计算模型
固-液旋流器分离数值模拟时,采用Standardk-ε、Realizablek-ε及雷诺应力模型(reynolds stress mode,RSM)等[13-16]。Rudolf 等[17-18]使用各种湍流模型对水力旋流器进行数值分析,结果表明RSM 湍流模型能较好地预测各向异性,同时也证明了RSM 湍流模型是与实验最相近的模型。隋元伟等[19]对比旋流器模拟中的不同模型进行分析,结果显示了雷诺应力模型更加适合水力旋流器固-液分离模拟。因此,本文选用RSM 模型为湍流计算模型。固-液分离过程,入口混合液固相的体积分数较低(10%~12%)。故采用流体体积(volune of fluid,VOF)模型和离散相模型(discrete phase mode,DPM)来模拟旋流器的复杂流场以及砂粒的运动轨迹,并得出速度分布以及压力分布规律,探究最佳工况。
1.3 边界条件设置
液相边界设置:入口为速度入口,其初始速度大小为10 m/s,底流口与溢流口均为压力出口。选取壁面滑移系数为0.5,旋流器壁面采用静止无滑移边界条件。模拟固-液分离时,固相砂粒粒径分别为 5、10、15、20、30、40 μm 和 50 μm,其入口速度与液相相同。
砂粒边界设置:采用DPM 砂粒模型,固-液旋流器入料管为砂粒进口,溢流口设置为escape(逃逸),底流口设置为trap(捕捉),旋流器内壁为完全反射。
1.4 网格无关性验证
为确保模拟计算结果的准确,需要进行网格无关性验证。如图2 所示,其中图2(a)为总压数值图,图2(b)为切向速度分布数值图。从图2 中可以看出,当模型网格数量达到5×105时,总压变化小,切向速度随网格数的加大变化较小,进一步增加网格未对计算结果造成影响,综合网格数量对混合液总压和切向速度的影响,选取网格单元数为5×105的模型进行计算。

图2 网格无关性验证:(a)总压,(b)切向速度分布Fig.2 Grid independence validation:(a)total pressure,(b)distribution of tangential velocity
2 结果与分析
2.1 流场压力分析
旋流器内部流场压力和压力降对旋流器分离效率及能耗具有重要影响。旋流器属于轴对称结构,图3 为X=0 时轴线截面的压力云图,研究不同入口流量为5~10 m3/h 时压力变化关系。
从图3 中可以观察到,X=0 截面上不同流量下压强呈对称分布,旋流器内同等半径处压强基本相等。随着入口流量的不断增大,流场内各点压力值也不断增大。在半径方向上,越靠近轴芯时压强越小,伴随着负压产生。
2.2 砂粒运动轨迹
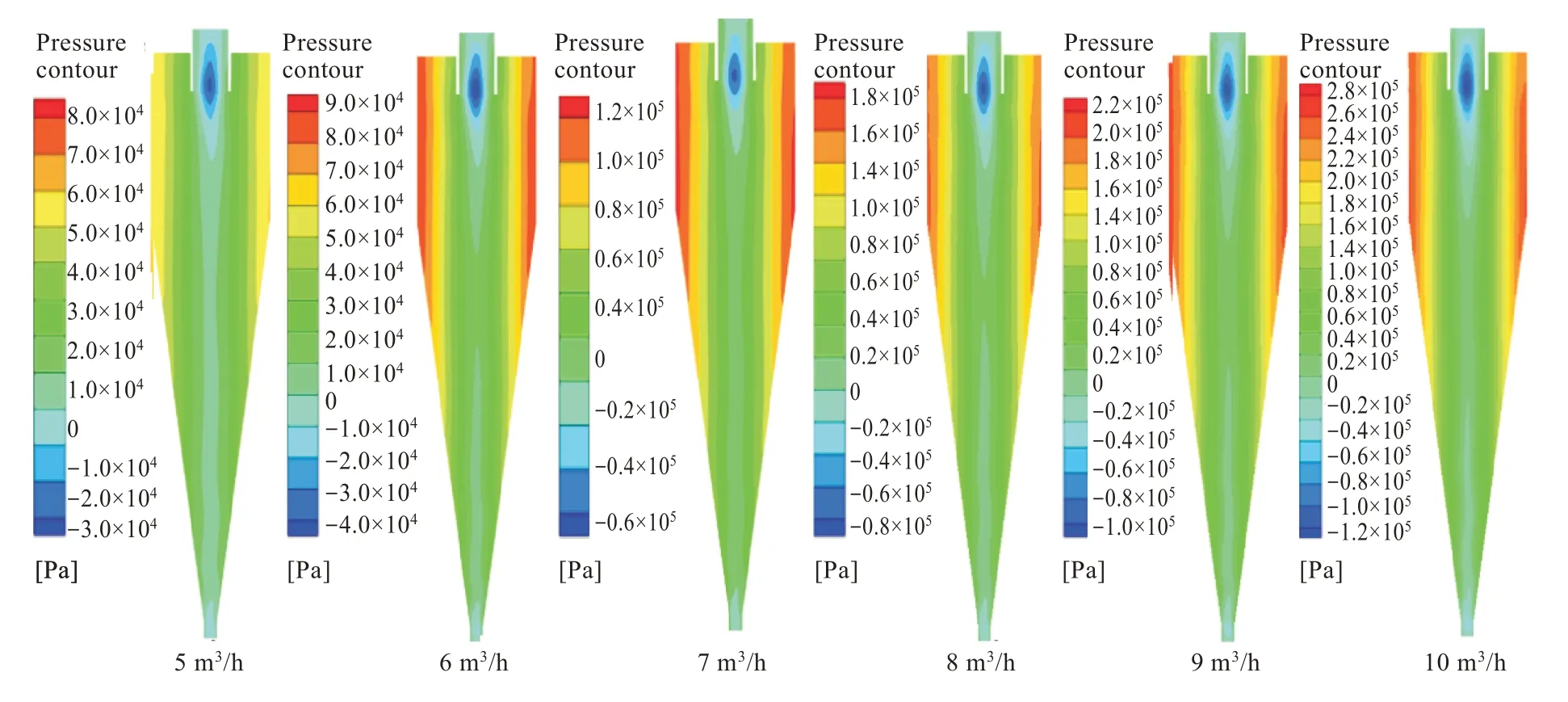
图3 X=0 截面处压力云图Fig.3 Pressure nephograms at X=0 section
在运用VOF 模型模拟水相流场且收敛的条件下,加入DPM 模型模拟出不同砂粒直径的运动轨迹。设置入口流量为10 m/s,取6 种不同粒径砂粒进行运动轨迹图模拟。如图4 所示,当砂粒粒径分别为5、10、20、30、40、50 μm 时,旋流器内部砂粒运动轨迹。从图4 中可知,砂粒沿旋流器壁面向下旋流运动,从底流口分离出来,砂粒粒径(5~10 μm)离心力较小,容易受到内旋流影响使砂粒没有沿着壁面运动,在向下运动的过程中容易受到向上内旋流干扰从顶部溢流口流出。而当砂粒粒径由20 μm 增加到 50 μm 时,砂粒所受到的离心力逐渐增大,运动轨迹越靠近壁面,从而导致底流口更容易捕获大直径砂粒。因此,随着砂粒粒径增大,5~10 μm 的分离效率降低,而大于砂粒 10 μm 分离效率升高的。
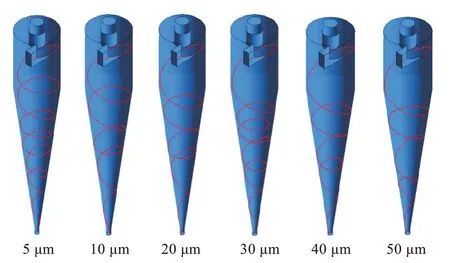
图4 砂粒运动轨迹图Fig.4 Sand trajectory diagrams
2.3 旋流器的分离效率
固-液旋流器的性能主要取决于分离效率。不同结构和操作工况下旋流器分离效率变化很大,而操作参数是分离效率最主要的影响因素。本文研究了不同操作参数下分离效率的规律。
图5(a)是入口流量与旋流器的分离效率图。由图5(a)可知,当入口流量设为5、6、7、8、9、10 m3/h时,随着砂粒入口流量的增大,旋流器分离效率先升高后降低。因为在入口流量较小时,旋流场尚未形成,进入的砂粒很容易直接从顶部的溢流口直接流出,从而降低旋流器的分离效率。当砂粒的直径一定时,流量增大导致旋流器内离心力的增大,使得砂粒分布在旋流器内表面,从而降低了内旋流和外旋流中间部分砂粒分布数量,使更多的砂粒向下运动在底流管被捕获,从而提高了旋流器的分离效率。当入口流量继续增大会使内流场湍流强度加大,导致旋流器内部开始出现循环流和短路流,使砂粒从旋流器入口进入后,直接从溢流口逃出,从而降低了旋流器的分离效率。
图5(b)是入口流量为10 m3/h 时旋流器中砂粒分离的迁移效率图,也就是不同砂粒粒径的分离效率。由图5(b)可知,当砂粒粒径为 30~50 μm时,旋流器分离效率接近100%。这是因为粒径为30~50 μm 砂粒分散在旋流器壁面附近,不易受到内旋流干扰。砂粒在重力和离心力作用下沿壁面向下运动从底流口流出,而粒径小的砂粒由于受到的离心力较小,不全分布在旋流器内壁处,容易处于外旋流和内旋流的中间区域,在向下运动的过程中容易受到内旋流的影响从上方溢流管逃出,从而降低旋流器的分离效率。
图5(c)是不同砂粒浓度对旋流器分离效率的影响。由图5(c)可以看出,随着砂粒浓度的增大,在砂粒浓度从1 g/m3增大到8 g/m3时,旋流器对不同粒径的砂粒的分离效率均增大。当砂粒浓度达到10 g/m3时,砂粒的分离效率开始下降。当浓度增大时,小砂粒分离效率增大的幅度要比大砂粒增大的幅度大,即浓度越大,小砂粒分离效率增加得越多,大砂粒分离效率增大相对较小,浓度超过一定值反而会有所下降。并且,随着砂粒浓度的增大,小砂粒分离效率增大,大砂粒分离效率增速缓慢。当砂粒浓度到达一定值时,旋流器对不同砂粒直径的分离效率会趋于一个稳定值,大砂粒在浓度较低时就趋于稳定,小砂粒则要在浓度较高时才趋于稳定。所以,混合液中砂粒浓度的增加,旋流器对小砂粒分离效率增大的幅度要比大砂粒增大的幅度要大。

图5 影响旋流器分离效率的因素:(a)入口流量,(b)砂粒直径,(c)砂粒浓度Fig.5 Factors affecting separation efficiency of cyclone :(a)inlet flow,(b)sand particle size,(c)sand concentration
3 结 论
本文针对工业级水力旋流器,借用数值模拟技术对旋流器内压力场和砂粒运动轨迹进行研究,同时对旋流器的分离效率进行分析,可得到以下结论:
1)通过数值模拟研究了复杂旋流场中的压力分布及砂粒在流场中运动轨迹。在不同流量下压强呈对称分布;当入口流量从5 m3/h升高为10 m3/h时,从轴心到旋流器内壁压强逐渐升高,压力数值不断增大,但旋流器同等半径处的压力保持不变。在流场稳定的条件下,利用DPM 模型模拟砂粒在流场中的运动轨迹,发现粒径大于10 μm 的砂粒运动轨迹越靠近旋流器壁面,砂粒粒径为5~10 μm容易随内旋流从溢流口逃出。 随着砂粒粒径的增大,旋流器的分离效率逐渐增大,砂粒粒径30~50 μm 时,旋流器的分离效率趋近100%。且在砂粒粒径为40 μm 时,旋流器的分离效率达到最大,其分离效率为97.5%。
2)入口流量为 5~9 m3/h 时,旋流器分离效率与入口流量呈正相关。当入口流量由5 m3/h 增加到 9 m3/h 时,砂粒粒径为 5~25 μm 的分离效率提高21.5%,砂粒粒径为30 μm 分离效率提高至97.3%,砂粒粒径大于30 μm 的分离效率趋于100%。分离效率达峰值时流量为9 m3/h。随着流量的继续增大,分离效率开始减小。当流量为10 m3/h 时,5~10 μm 砂粒分离效能降低 5.5%,大于10 μm 砂粒分离效率趋于稳定。
3)砂粒浓度越大,旋流器分离效率越高。小砂粒分离效率达到稳定所需砂粒浓度要比大砂粒砂粒浓度高。当砂粒浓度从1 g/m3升高至8 g/m3时,砂粒粒径为5 μm、10 μm 和大于10 μm,分离效率的增幅分别为8.6%、9.7%和5%。当砂粒浓度继续增加至 10 g/m3,砂粒粒径为 5、15、20 μm 和30 μm,砂粒分离效率分别降低 1.5%、2.3%、4.7%和3.4%。

