基于综合性能评价指标的智能PID参数优化与应用

张永亮 赵 众

（北京化工大学信息科学与技术学院）

工业控制回路的自控性能是其自动化水平的重要体现，在石油、化工及冶金等传统工控过程中，常规PID控制器的应用占到90%以上，一般在运行初期性能良好，但随着工况变化和设施维护不及时等原因， 导致其控制性能逐渐下降，无法达到原设计目标。

控制器优秀的控制性能是保证生产安全、提高产品质量和产能、减少员工劳动强度的重要条件。 目前，用于评价控制器自控性能的指标主要有随机性和确定性。 Harris T J最早提出随机性指标评价方法——基于最小方差控制基准（MVC）的性能评价［1］。Huang B提出一种考虑控制量约束的线性二次型高斯基准（LQG）性能评价方法［2］。Eriksson P G和Isaksson A J在MVC的基础上加入控制权重和误差权重，提出广义的最小方差基准［3］。 将过去一段时间历史数据提取的评估值作为性能评价基准与现在时间段的数据作比较，被称为基于历史数据基准（HIS）的评价方法［4］。经过不断改进和完善，最小方差控制基准也被应用到复杂控制器的性能评价中。Desborough L和Harris T J将最小方差控制基准评价方法应用到评价单变量的前馈-反馈系统控制性能中［5］。 Ko B S和Edgar T F根据串级控制系统特性改进了最小方差控制基准，以此评价串级控制系统的控制性能［6］。 Yu J和Qin S J通过改进最小方差控制基准，将最小方差控制基准评价方法推广到多变量控制系统［7］。 确定性评价方法主要体现跟踪设定值的能力和控制系统的抗干扰鲁棒稳定性，例如通过对象模型得出动态过程特性性能指标调节时间、上升时间及稳态误差等［8］。 Massimiliano V和Antonio V根据系统上升时间等动态特性指标，计算得到性能指标评价设定值的跟踪性能［9］。 王谦等用一种鲁棒稳定性性能指标结合绝对误差积分（IAE）性能指标评价控制系统的控制性能［10］。陈晨等采用时间乘平方误差积分（ITSE）指标评价串级回路主回路的控制性能［11］。

除了硬件设施损坏导致的控制器控制性能下降之外，大多数情况下可以通过控制器参数整定来重新恢复其控制性能。 因此，控制器参数整定成为恢复控制器性能的核心问题。 目前，PID参数还需要工程师根据个人经验调节， 费时费力。因此，智能PID控制［12］得到了学者们的广泛关注。智能PID控制是将智能算法（如模糊控制算法［13］、遗传算法［14］及神经网络算法［15］等）与常规PID控制器相结合，可以根据实时数据自动辨识对象模型， 并自动优化PID参数， 实现控制系统的 “自愈”。 因此，智能PID控制既有智能算法的自适应性和“自愈”能力，还具有普通PID控制器可靠性高的优点。例如Massimiliano V和Antonio V用电脑程序模拟人工调节PID参数的试凑法， 实现了对控制器参数的自动整定［9］。 胡包钢和应浩讨论了模糊PID控制的相关问题［16］。 张继荣和张天提出一种惯性权重引入余弦调整的粒子群优化算法（IWCPSO）用于优化PID参数［17］。 吕磊等采用蝙蝠智能算法优化PID参数［18］。 戴丽等针对经典智能优化算法在PID参数整定时存在早熟收敛和易陷入无效循环的问题，提出一种改进细菌菌落的优化算法［19］。

针对由于系统工况变化、设施老旧以及维护不及时导致常规PID控制器的自控性能无法满足要求的问题，提出一种基于综合性能评价指标的智能PID参数优化方法，用以准确评价常规PID控制器的控制性能并提高其控制性能。

1 性能评价指标

1.1 闭环模型辨识

典型的闭环控制回路如图1所示。

图1 典型的闭环控制回路

利用子空间辨识［20］方法辨识闭环模型，其离散状态空间模型表达式为：

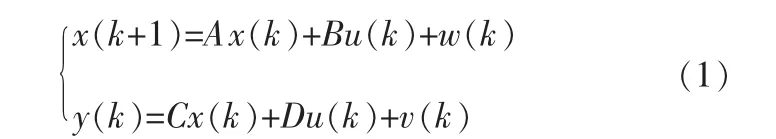
其中，A、B、C、D为系统模型矩阵；x（k+1）∈Rn表示下一时刻过程状态量；x（k）∈Rn表示过程状态量；u（k）∈Rm表示控制器输出；w（k）∈Rn表示系统过程中的噪声干扰；y（k）∈Rl表示系统输出；v（k）∈Rl表示系统过程中的测量噪声干扰。

闭环控制回路的脉冲响应模型为：

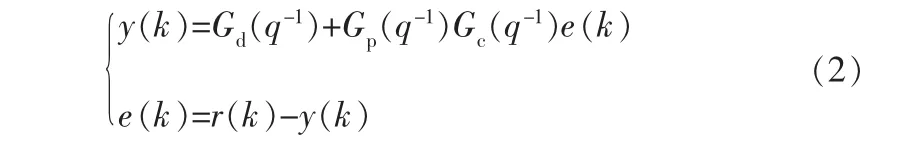
用Ut表示将来的输入；Vt表示将来的v（k）测量噪声干扰；Wt表示将来的w（k）系统过程噪声干扰。Ut、Vt、Wt为Hankel矩阵。则式（2）可以转换为：

其中Yt为输出观测向量；Γt为可观测矩阵；Xt为系统状态序列；Pt为输入下三角Toeplitz矩阵；Qt为测量干扰噪声下三角Toeplitz矩阵。Qt与Pt相似，只是Qt中的D=0；B为单位矩阵。

子空间模型辨识步骤分为两步。

首先， 确定可观测矩阵Γt或系统状态序列Xt，通过投影消除测量噪声、过程噪声和未来输入项，得到Rt=ΓttXt，对Rt进行奇异值分解（SVD），可得：

最终得到的系统传递函数为：

1.2 快速性指标

响应速度是评价控制系统好坏的重要指标，因此提出用跟踪指数（Track Index，TI）表示实际控制系统的跟踪速度。 跟踪指数TI的基准为开环系统的稳态时间，计算式为：

其中，Tc为闭环稳态时间；To为开环稳态时间。

1.3 稳定性指标

系统稳定性是指系统受到外部干扰而偏移稳态后恢复稳态的抗干扰能力，因此提出稳定指数（Stability Index，SI）表示实际控制系统的稳定性。 稳定指数SI的计算式为：

其中，SVi为系统的设定值；PVi为系统输出；n为采集数据个数；μ为要求的控制精度，取值范围为3%～5%。

1.4 准确性指标

系统能否准确跟踪设定值是评价控制器的关键指标。 因此， 提出精确度指数（Accuracy Index，AI） 表示实际控制系统准确跟踪设定值的能力。 精确度指数AI的计算式为：

1.5 性能评级

综合性能等级根据跟踪指数、稳定指数和精确度指数得出，综合评级分为优秀（excellent）、良好（good）、较差（fair）、极差（poor）4个等级。

笔者采用决策树——分类与回归树（CART）算法［21］制定评价规则。 分类与回归树算法采用基尼系数［21］最小化准则选择跟踪指数、稳定指数和精确度指数评价指标的特征分类点，并生成决策树。基尼系数Gini（p）可以表征训练数据样本集的纯度，基尼系数越小则样本纯度越高，计算式为：

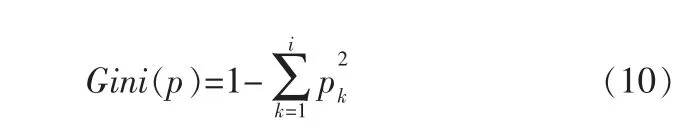
其中，pk表示第k类的概率。

决策树建立步骤如下：

a. 将训练数据样本排序，将相邻数据的平均值作为划分点；

b. 计算每个划分点的基尼系数，则该特征分类点（splitPoint）为基尼系数最小的划分点；

c. 根据3个特征的分类点生成决策树；

d. 采用错误率降低剪枝法（REP）优化决策树。

错误率降低剪枝法是将决策树中的每一个非叶子节点的子树替换成一个叶子节点，这样就产生了一个新的相对简化的决策树，使用检验数据样本比较替换前后两个决策树分类的正确率，将正确率最高的决策树作为最优决策树，从而达到优化决策树的目的。 通过分类与回归树算法得出跟踪指数、稳定指数、精确度指数的分类点分别为1.2、0.6、1.5。 最终的决策树如图2所示。

图2 决策树

根据决策树得出的具体评价规则见表1。 当综合评级为较差和极差时， 表明控制器性能下降，无法满足工艺控制要求，需要在线优化PID参数，恢复控制器性能。

2 PID参数优化整定

当评价结果显示控制器性能下降并且不能满足控制需求时， 则需要在线优化PID控制器的参数，用以提升控制器性能。 笔者采用内模控制原理［22］整定PID控制器参数，引入灵敏度函数和互补灵敏度函数调节控制系统的鲁棒性和跟踪性。 内模控制器的结构如图3所示。

图3 内模控制器结构框图

根据内模控制原理，反馈控制器Gc（s）和内模控制器GIMC（s）有如下关系：

灵敏度函数表征控制系统的鲁棒性，互补灵敏度函数表征系统对设定值的跟踪性能，具体如下：

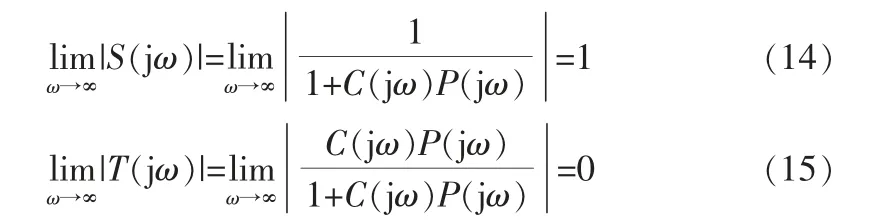
通常情况下系统是正则的， 则由式（14）、（15）可以看出，在理想状态下，闭环灵敏度函数为1，互补灵敏度函数为0，但是由于无法在全频段得到理想的控制性能，因此需要对灵敏度和互补灵敏度函数互相取舍后才能设计出控制性能优良的控制器。 例如可以取较小的灵敏度函数来提升控制系统的鲁棒性。

定义灵敏度对于所有频率的最大幅值为最大灵敏度函数MS；定义互补灵敏度对于所有频率的最大幅值为最大互补灵敏度函数MT。 对于一个控制性能优良的控制器， 最大灵敏度函数在［1.2，2.0］取值；最大互补灵敏度函数在［1.0，1.5］取值。 因此可以在此范围内设计控制器参数提升控制性能。 最大灵敏度函数MS和最大互补灵敏度函数MT的计算式为：

根据内模控制器设计原理，将对象模型分解为纯滞后环节、右半平面的零点部分Gm+（s）=1和最小相位部分Gm-（s），即：

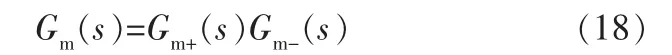
根据内模控制的对偶稳定性可知，内模控制系统稳定的必要条件是辨识的对象模型准确且GIMC（s）和Gm（s）都稳定。但是现实很难准确辨识系统模型。 当模型失配时，则需要引入滤波器f（s）提升鲁棒性。 由此得出内模控制器：

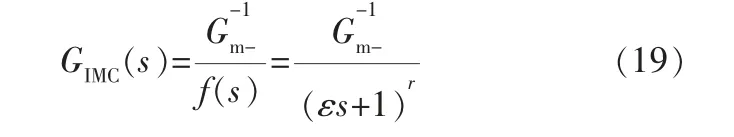
对于一阶惯性加时滞系统，由最大灵敏度函数、相位裕量和幅值裕量得出滤波器参数与最大灵敏度函数之间的关系：

其中，d为滞后时间。

根据稳定指数和精确度指数判断系统的鲁棒性，当鲁棒性差时，在最大灵敏度函数的取值范围内减小最大灵敏度函数， 以提升稳态裕量。通过调节滤波器参数ε调节最大灵敏度函数。 由最大灵敏度函数的取值范围可得滤波器参数的取值范围在（0.43～4.15）d。

一阶惯性加纯滞后系统的对象模型Gp（s）为：

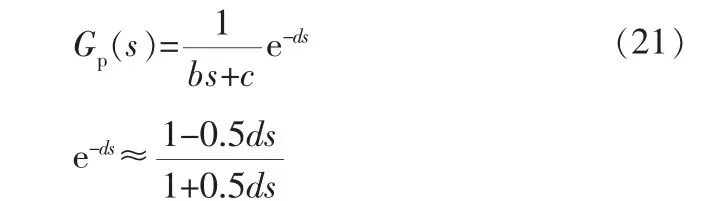
纯滞后环节e-ds采用一阶Pade近似展开。 将一阶惯性加纯滞后对象模型分解为Gm+（s）和Gm-（s）：

根据内模控制器和反馈控制器的关系得到反馈控制器的形式为：

PID反馈控制器的一般形式为：

根据s多项式同次项幂系数对应相等的原则即可求得PID控制器各项参数：

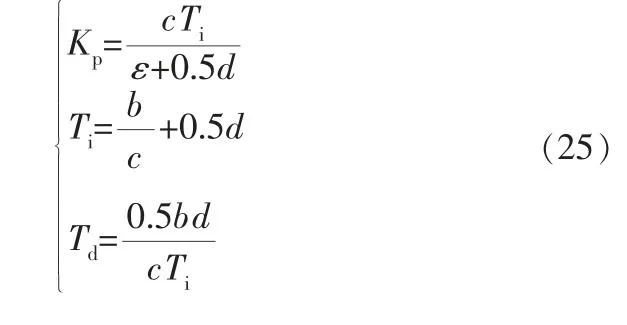
实际中，采用二阶加纯滞后模型表征温度和粘度高的流体对象才能得到满意的近似，其过程模型为：

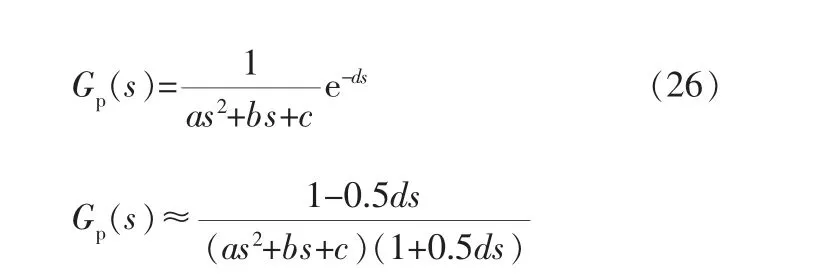
纯滞后环节e-ds同样采用一阶Pade近似展开。二阶加纯滞后模型的内模控制参数整定方法如下：

根据s多项式同次项幂系数对应相等的原则即可求得对于二阶加纯滞后系统的PID控制器各项参数：

3 基于综合性能评价指标的智能PID参数优化流程

基于综合性能评价指标的智能PID参数优化流程如图4所示。 在线采集控制系统数据，计算控制性能评价指标并判断控制器性能是否下降。 若控制性能下降无法满足控制要求， 则采用内模PID整定算法对PID参数进行整定，经工程师判断参数合理后应用于控制器，再次采集数据并判断控制器性能是否良好。

图4 基于综合性能评价指标的智能PID参数优化流程

4 仿真与工业应用

4.1 仿真及软件开发

基于综合性能评价指标的智能PID参数优化方法， 开发了相应的控制系统性能评价与自愈（Controller Performance Evaluation and Selfhealing，CPES）软件。在某化工企业对催化装置的100多个基础回路投用控制系统性能评价与自愈软件，实现实时监控控制器性能的功能。 现场应用系统结构如图5所示。通过OPC服务器采集过程数据，并储存在数据库中。 性能监控服务器读取实时数据，计算综合性能指标并判断性能是否下降，若性能下降则在线整定PID参数。 工程师判断整定的参数合理后应用于控制器。

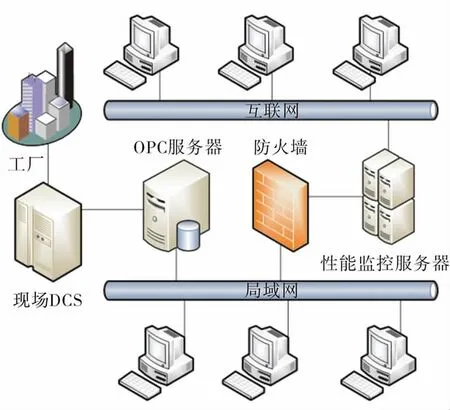
图5 现场应用系统结构示意图

CPES系统可以将性能指标和综合评价发布到企业管理信息网络。 工程师可以在性能监控服务器中访问企业局域网，查看所在车间的控制回路信息。 网络发布端可以更直观地看出某车间某装置控制回路的实际状况，也可以查看整个车间所有回路的整体控制状况， 如综合评级所占比例、综合自控投用率等。 利用网络发布系统可以及时发现问题，实现网上巡检，提高对控制系统的维护效率。 网络发布界面如图6所示。

根据实际工业控制系统，仿真搭建多个流量、温度、压力和液位的控制系统模拟实际工艺对象。其中模拟流量FIC1101控制系统如图7所示， 控制系统包括PID控制器、 二阶加纯滞后对象模型、随机干扰及OPC数据读写等模块。由此控制系统模拟实际工程产生过程数据，由OPC采集仿真实时数据用于性能评价。 PID控制器初始的PID参数为：比例系数P=0.75、积分时间I=0.2s、微分时间D=0.89s。

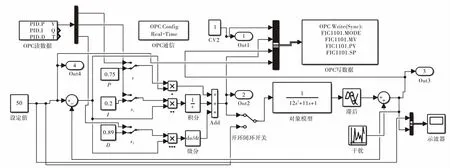
图7 模拟流量FIC1101控制系统

图8所示为整定前、 后的评价结果， 流量FIC1101控制系统评级结果为较差， 跟踪指数为2，表明响应速度较慢，跟踪性能差；精确度指数为5.83，表明控制系统不能准确跟踪设定值，存在较大振荡。 综合评级结果表明，该回路的控制性能不能满足控制需求， 因此启动PID参数优化功能。 经过整定后（图9） 的PID参数为P=0.514、I=0.083s、D=0.103s。 跟踪指数为0.53， 稳定指数为0.02，精确度指数为0.15，性能评级结果为优秀，表明控制性能恢复。

图8 流量FIC1101控制系统整定前、后的评价结果

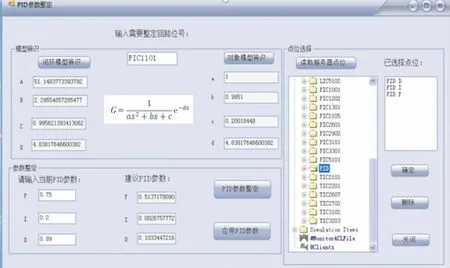
图9 流量FIC1101控制系统的PID参数整定结果

图10为控制器参数整定前、 后跟踪趋势对比，200s后为整定后的跟踪趋势。

图10 控制器参数整定前、后跟踪趋势对比

4.2 工业应用

将控制系统性能评价与自愈软件投用到某化工企业催化装置的100多条基础控制回路中，催化装置的自控率从投用前的69.89%逐步提升，最终达到了96.56%；装置仪表平稳率的平均值从投用前的50.0%提升到了95.5%，效果良好。

以流量FIC2501控制系统为例，整定前、后的性能评价结果如图11所示。 整定前的PID参数为P=0.3、I=0.5s、D=0.02s，评价结果为较差，跟踪性能差，系统存在较大波动，实际值无法准确地跟踪设定值，且操纵变量变化幅度大。 整定后的PID参数为P=0.1、I=1.0s、D=0.20s， 评价结果为优秀，波动幅度减小，阀门操作平滑，满足现场工艺控制要求。 实际控制曲线如图12所示，其中设定值为12t/h。

图11 流量FIC2501控制系统整定前、后的性能评价结果

图12 整定后流量FIC2501的实际控制效果

5 结束语

智能PID参数优化是使用在线数据评价控制系统性能， 当性能下降无法满足控制要求时，在线优化PID参数，提高控制器性能。 笔者提出的基于综合性能评价指标的智能PID参数整定方法，在不影响正常工况运行的情况下适当调节控制系统的设定值，并采集实时闭环数据评价控制器性能。 综合评价指标能更全面地表征控制系统的控制性能，提高了控制器性能评价的准确性和实用性。 在性能下降时，采用基于内模控制的PID参数整定方法优化PID参数， 并结合灵敏度函数和互补灵敏度函数提升控制系统的鲁棒性和跟踪性能。 根据此方法开发了控制系统性能评价与自愈软件。 仿真和工厂实际应用结果都表明：使用此方法可以有效地提高控制系统的控制性能，且控制系统具有良好的自愈性，说明该方法具有可行性和有效性。