基于极点配置的PMSM电流环PI控制器设计

许文波 焦玮玮 潘 龙

北京精密机电控制设备研究所，北京 100076

0 引言

在运载火箭/弹道导弹各分系统中，伺服机构是运载火箭/弹道导弹的关键组成部分。永磁同步电机(PMSM)具有结构简单、体积小、重量轻、损耗小等优点，机电伺服机构组成简单，具有可靠性高、维护保养要求低，测试、使用方便等特点，因此在航天型号研制中得到了广泛应用[1-3]。基于PMSM的伺服控制系统是一个包含位置、转速、电流环的多闭环系统。其中，作为最内环的电流环决定着电流的跟踪性能，响应的快速性，直接影响PMSM的输出电磁转矩，进而影响机电伺服机构的性能。

在PMSM电流环控制方式上，近年来许多先进的电流控制方法不断被提出，如非线性预测控制、反推控制、模糊PI控制、神经网络控制、滑模控制等[4-8]。工程中PMSM驱动系统多采用结构简单、易于实现、性能良好、对控制对象参数变化不敏感的PI控制器。因此，对于PMSM驱动系统比例积分(PI)控制器参数设计和整定方法的研究极具工程价值。

PI控制器的参数整定方法通常分为2类：1)基于实验的方法，如Ziegler-Nichols整定法；2)通过对被控对象进行建模，然后通过测量或辨识模型参数计算得到控制器参数。1984年Astrom和Hagglund首次提出了基于幅值裕度和相角裕度的PID参数自整定方法[9]。文献[10]旨在通过幅值裕度和相位裕度获得最佳闭环特性的PID参数。文献[11]基于PMSM调速系统的频域模型，推导出了电流环PI控制器参数Kp和Ki的解析计算式，通过这些解析式，实现设定的期望开环截止频率和相位裕度，但并未考虑系统的零极点分布及对系统性能的影响进行分析。文献[12]研究了基于主导极点和相位裕度的PID整定算法，通过在控制器的零点配置主导极点的方式得到PID整定式，但未考虑系统零点的影响。文献[13]未考虑系统零点对阶跃响应瞬态分量的影响。文献[14]提出了通过对PI控制参数取值的约束进行零极点抵消的方法，但控制参数的取值受到了限制。

本文通过零极点分布对系统性能的影响分析，推导了零极点抵消的条件，确定系统极点的形式，再根据期望的系统带宽及超调确定期望极点并进行PI参数设计。通过仿真分析验证了本文提出方法的正确性，具有较强的工程应用参考价值。

1 预备知识

考虑SISO系统，对给定线性定常系统的状态空间描述为

(1)

其中，A为n×n常阵，B为n维列向量，C为n维行向量；u为对系统施加的控制，若u取为系统状态x的线性函数和一个输入向量v，可表示为

u=-Kx+v

(2)

式中，K=[K1,K2,…,Kn]为n维行向量。

代入式(1)，得到闭环系统的状态方程为

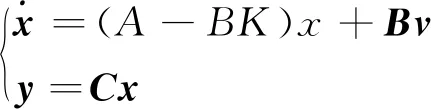
(3)

通过(1)、(3)两式比较，所谓极点配置，就是通过选择反馈矩阵K，将闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的动态特性。而控制系统的性能主要取决于系统极点在根平面上的分布。因此，在系统设计中，通常是根据对系统的品质要求，规定闭环系统极点应有的分布情况。

由现代控制理论可知，线性定常系统(1)可通过状态变量反馈来任意配置其全部极点的充要条件是该系统为完全能控的。因此，对于一个完全能控的线性系统的极点配置问题，实际上转化为求解状态反馈增益矩阵K。

引入状态反馈后闭环系统(3)的特征方程可以写成

|sI-A+BK|=sn+α1sn-1+…+αn=0

(4)

设给定的闭环系统的n个所期望的极点是(λ1,λ2，…，λn)，则有

(5)

分别令αi=βi(i=1，2，…，n)则可求解状态反馈增益矩阵K。

2 PMSM电流环数学模型

2.1. PMSM的数学模型

在分析永磁同步电机的数学模型时，常做如下假设：

1)忽略磁路饱和，不计铁心中的涡流和磁滞损耗；

2)三相绕组对称，在空间上互差120°电角度；

3)转子上没有阻尼绕组，永磁体也没有阻尼作用；

4)气隙磁场呈正弦分布，忽略高次谐波的影响。

在d-q旋转坐标系下，Ld=Lq=L，采用id=0控制，PMSM的电压方程、转矩方程以及机械运动方程可分别表示如下：

(6)

(7)

(8)

式中，ud，uq为d、q轴电压；iq为q轴电流；ψf为永磁体磁链；R，L为定子绕组电阻和电感；Ke为电机的反电动势常数；ω为电机的机械角速度，Kt为转矩常数；J为转动惯量；b为粘滞摩擦系数；TL为负载转矩。

2.2 PMSM电流环PI控制

作为数字控制系统内环的电流环，主要实现d、q轴电流的快速跟随及电流限幅，其采样频率远高于速度环采样频率，具有较高的控制环路带宽，在本文中设逆变器的电压增益为Kinv，忽略滤波器及逆变器动态特性对电机转速特性的影响，电流和速度控制器均采用经典PI结构，即

(9)

综合式(6)～(9)，可以得到PMSM电流环控制系统框图如图1所示。

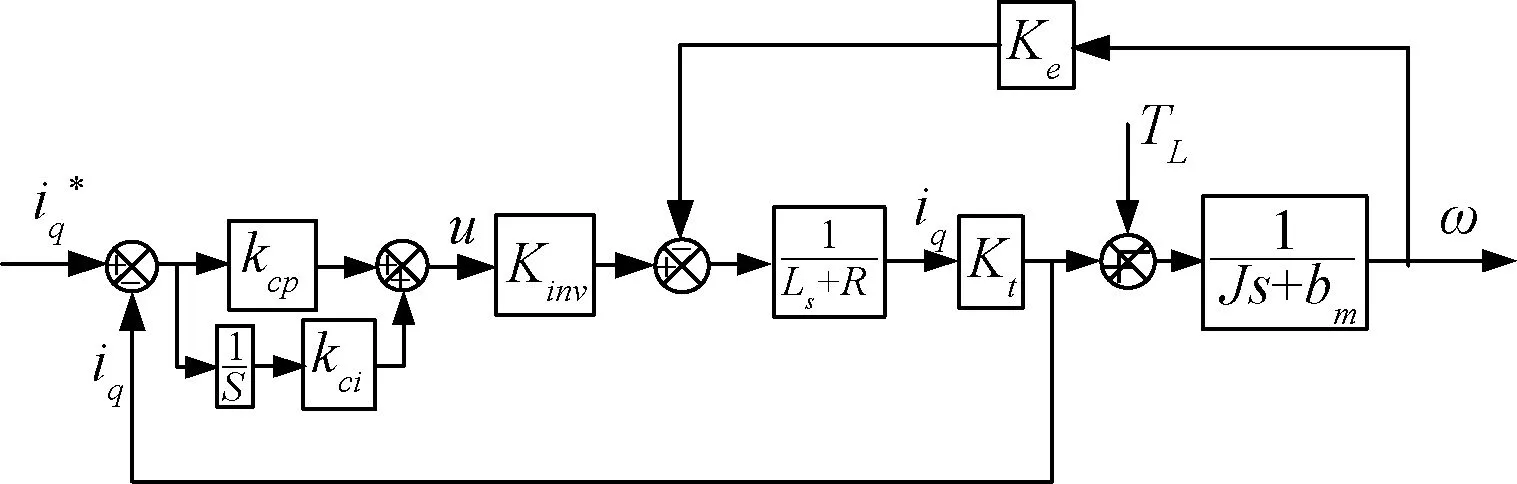
图1 PMSM电流环PI控制框图

2.3 PMSM电流环PI控制系统状态空间描述

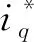
图2 忽略反电动势PMSM电流环PI控制框图

iq=x1

(10)

写成矩阵形式

(11)

3 基于极点配置的PI控制参数设计

3.1 电流环能控性分析

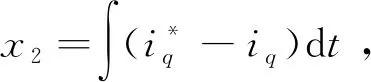
由式(10)～(11)可知，通过状态变量的选取，PMSM电流环PI控制系统可以转换为全状态反馈控制问题。系统(10)可通过状态变量反馈来任意配置其全部极点的充要条件是该系统为完全能控的，即

rank[B⋮AB]=2

(12)

对于本文考虑的SISO系统，式(12)等价于

det([B⋮AB])≠0

(13)

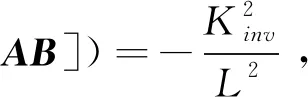
3.2 电流环的零极点分析

(14)

其中,I为单位矩阵，将矩阵代入并经化简，其零、极点特征方程分别为

kcps+kci=0

(15)

Ls2+(R+Kinvkcp)s+Kinvkci=0

(16)

对比式(9)和(15)，该零点正是由PI控制器引入的电流环开环零点，进而成为闭环零点，该零点为一负实零点，如下

(17)

电流环闭环极点为

(18)

由式(18)可知，PI控制器的比例增益kcp决定了电流环极点与虚轴的距离，即决定了电流环的快速性；积分增益kci决定了电流环极点的虚部和闭环零点，极点虚部影响系统的超调和振荡；电流环闭环零点的存在会缩短电流环的调节时间和增大其超调。

电机控制中，为了获得良好的快速性，电流环极点与虚轴应有一定距离，kcp不宜太小，也允许电流环存在一定的超调。但需避免电流环超调引起的大电流冲击电力电子器件，系统的阻尼比仍然不能太小，kci不能太大。

先讨论电流环控制系统具有一对共轭复数极点的情况：

假设存在一组控制参数kcp,kci，使得电流环控制系统存在一对共轭复数极点，则

(R+Kinvkcp)2<4LKinvkci

(19)

(20)

再假设该系统的一对极点为pc1,2=-a±jb，其中a正实数，b为非负实数，代入特征方程式(15)可得其零点如下

(21)

对具体电机而言，R和L确定，故为获得快速的调节过程，电流环控制系统的极点距离虚轴不能太近，通常存在a>R/L。由于闭环零点的存在，为了有效抑制电流环超调，系统阻尼比不能太小，当系统阻尼比大于0.707时有a>b，此时有

(22)

式(22)表明，闭环零、极点与虚轴距离之比小于2，因此闭环零点对系统性能的影响不能忽略；同时一对共轭复数极点又无法与闭环零点抵消。

由自动控制原理可知，此时电流环将存在较大超调振荡。

再讨论电流环控制系统具有两个负实极点的情况：

设该系统的一对极点为pc1=-a和pc2=-b，其中a、b均为正实数，且a>b，则下式成立

(23)

比较系统零、极点之间的关系有

(24)

由式(24)可知

1)当b>R/L时，闭环零点位于两极点右侧；

2)当b=R/L时，闭环零点与一极点重合；

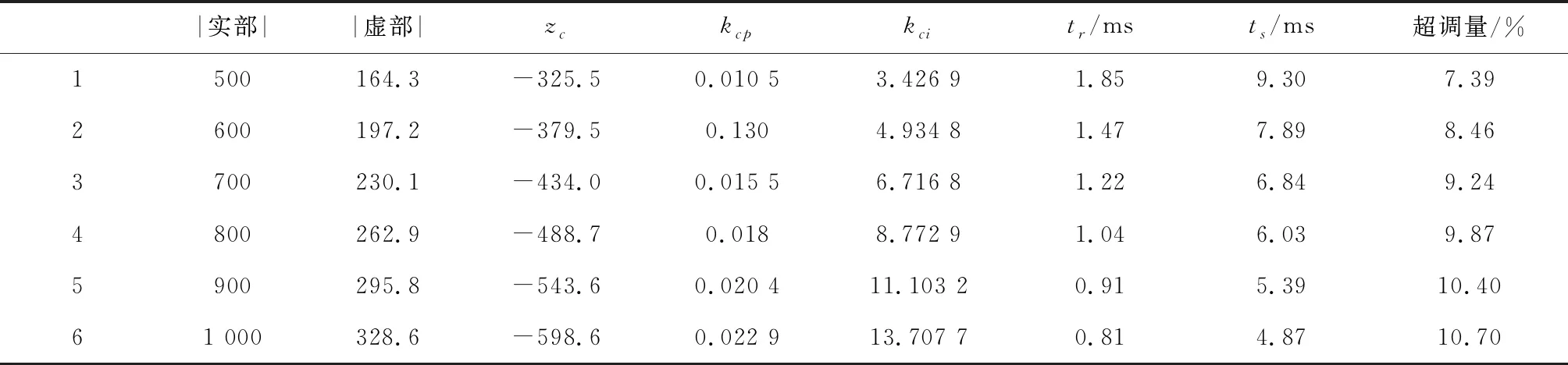
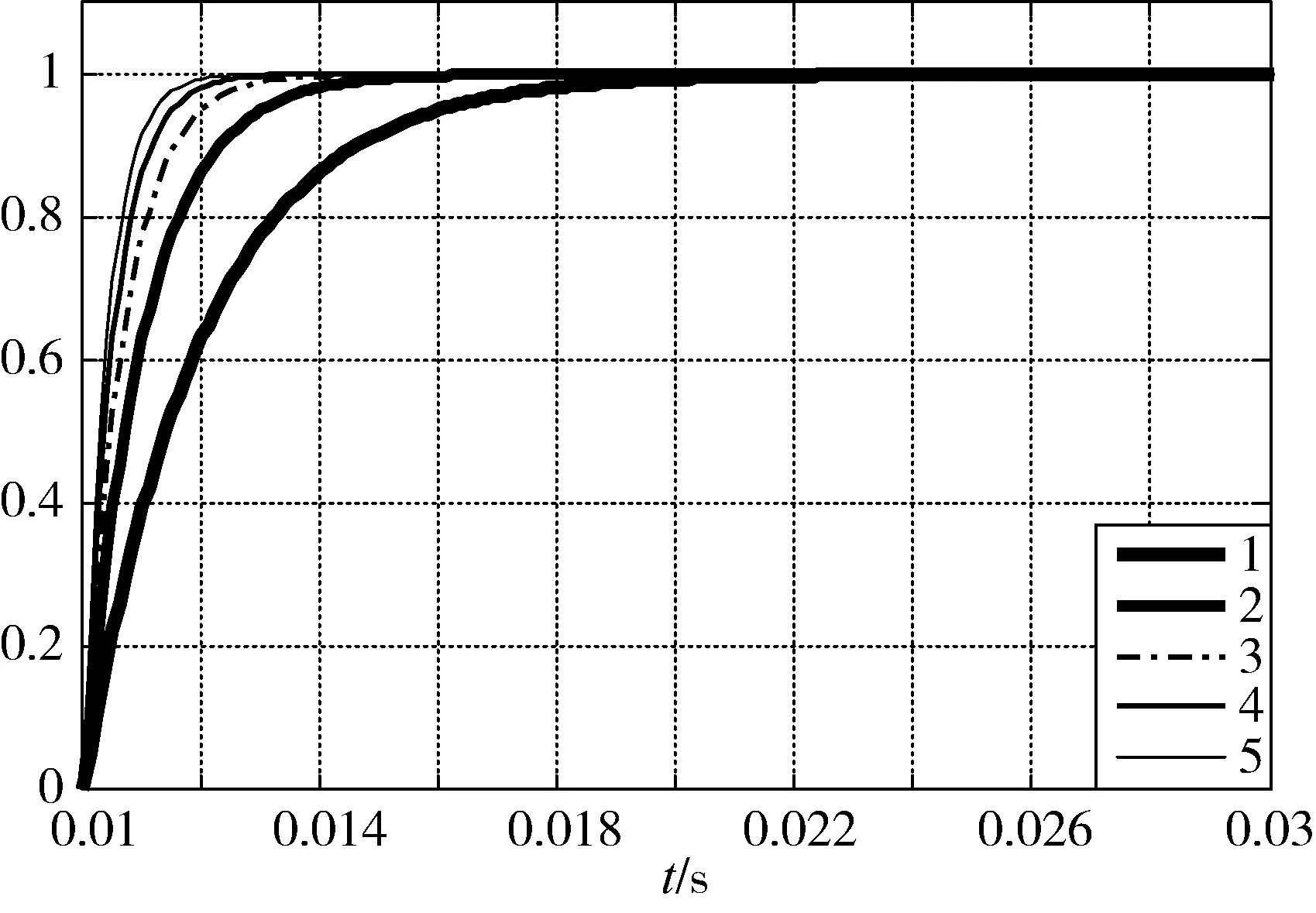
3)当b

在理想情况下，不考虑SVPWM电源逆变器控制周期、开关延迟、死区时间、滤波网络和数字控制延时等，根据零、极点的相对位置，当b≤R/L时，电流环无超调。但实际工程应用时，系统存在开关延迟等非理想因素，可适当将b值取得小一些，但b值太小可能会导致电流环跟踪存在静差，或跟踪速度过慢。

进一步分析式(24)有

(25)

若b≈R/L或a≫b，为了保证系统的快速性有a≫R/L，则下式成立

zc-pc2≈0

(26)

式(26)表明，通过对电流环极点配置，基本可以抵消闭环零点对电流环性能的影响，电流环的性能取决于极点pc1=-a，在研究速度环时，若把电流环等效为一阶惯性环节，其闭环带宽ωcb=a(rad/s)。

3.3 电流环的极点配置及PI参数设计

逆变器工作时易产生复杂的开关谐波，为了避免引入干扰，希望开关谐波处于系统的高频段，即开关频率应大于10ωcb，即

(27)

式中Tinv为逆变器控制周期。

(28)

则

(29)

实际系统中存在多种非理想环节，在进行电流环极点配置时对a的取值可保守一些，以保证电流环的稳定裕量。

综上，电流环极点配置的原则和步骤为

1)根据期望的速度环闭环带宽及逆变器的控制周期确定其远极点，保留一定的稳定裕量，保证电流环不产生振荡；

2)选择和调整其近极点，使电流环的跟踪速度、跟踪静差和超调量满足要求；

3)根据期望极点，按式(23)计算kcp和kci。

4 仿真结果

利用Matlab中的SIMULINK模块进行仿真，仿真使用如图2所示的PMSM电流环PI控制系统。

电机参数按某型PMSM实验数据进行选取，具体如下：

L=0.002H，R=0.292Ω，J=1.2×10-4kg·m2，bm=0.000 015Nm·s，Kt=0.225Nm/A，Ke=0.149V·rad/s；取逆变器放大系数Kinv=158.4V。

其电气时间常数为

Te=L/R=0.0067=1/149(ms)

(30)

首先按一对共轭复极点配置进行仿真验证，为了验证系统具有较大的超调量，在极点配置时取极点的阻尼比ζ=0.95，由表1可以看出，在共轭复极点配置策略下，系统存在一个较大极点，kci取值较大，尽管所配置极点阻尼比很大，但由于系统零点无法与极点进行抵消，因此系统存在较大的超调，调节时间较长。图3为共轭复极点配置策略下的系统阶跃响应曲线。

表1 共轭复极点配置策略下系统参数

图3 共轭复极点配置策略下系统阶跃响应曲线

表2和图4分别为固定远极点配置策略下系统参数和阶跃响应曲线，将系统远极点取固定值pc1=-a=-2000；与表1结果相比，得到的kci参数均较小，随着近极点远离虚轴，kci取值逐步增大，系统零点也远离虚轴，系统响应加快；在此策略下系统的近极点pc2和零点zc基本重合，当近极点pc2=-R/L=-149时，与系统零点重合，系统达到临界超调状态；当极点与虚轴太近时，积分效果不明显，系统的调节时间很长。

表2 固定远极点配置策略下系统参数

图4 固定远极点配置策略下系统阶跃响应曲线

表3 和图5为固定近极点配置策略下系统参数和阶跃响应曲线，随着极点远离虚轴，kcp，kci都逐渐增大，系统响应加快，因近极点pc2=-R/L=-149，系统均未出现超调，但当电流环达到一定带宽后，再继续增大对系统快速性影响不大，反而会因电源逆变器控制周期、死区等非理想环节，降低电流环的稳定裕量。

表3 固定近极点配置策略下系统参数

图5 固定近极点配置策略下系统阶跃响应曲线

图6 为用一阶惯性环节代替非理想环节的电流环阶跃响应曲线，由于非理想环节的存在导致pc1=-2500时，电流环出现超调，通过调整任一极点均可避免系统超调，但相比之下，调整pc2能够有效消除系统的超调，且对系统的快速性影响不大。

图6 考虑非理想环节的系统阶跃响应曲线

综上，仿真结果表明：当电流环配置一对共轭复极点时，将产生较大超调；验证了本文提出的通过零极点抵消的极点配置方法能够有效抑制或消除系统的超调，提高系统的稳定性。

5 结语

针对PMSM电流环PI控制，提出了一种极点配置方法，通过分析推导了系统零极点抵消的条件，并根据期望极点确定PI控制参数，仿真结果验证了所提出整定算法可行有效。该方法简洁明了、算法物理意义明确，具有较强的工程应用和推广价值。