无人机三维航迹规划的量子粒子群优化算法*

赵红超 周洪庆 王书湖

1. 烟台南山学院高端航空铝合金材料协同创新中心，山东龙口 265713 2. 海军航空大学 岸防兵学院，烟台 264001

0 引言

航迹规划技术是无人机任务规划系统中重要的核心技术之一，它是在综合考虑到达时间、油耗、威胁以及飞行区域等因素的前提下，为无人机规划出最优或者满意的飞行航迹，以保证圆满地完成飞行任务[1-2]。无人机在三维环境空间中执行任务，跨越空间范围大、环境复杂，而且无人机自身约束条件较多；因此，航路规划算法需要在计算复杂度、搜索时间和航路代价之间做好折中处理，以满足实际工程任务要求。目前，国内外研究者针对航迹规划问题提出了许多规划算法，每种算法都有自身的优缺点和适用范围。按照规划决策可以分为传统经典算法和现代智能算法2大类。常用于无人机航迹规划的传统经典算法包括：Dijkstra算法、模拟退火算法、Dubins曲线法、人工势场法、快速扩展随机树及其改进型算法等。现代智能算法包括：A*算法、遗传算法、蚁群优化算法、粒子群优化(particle swarm optimization，PSO)算法、鸽群算法等。文献[3]针对多无人机协同航迹规划问题，研究了一种蜂群与A*混合算法，规划出的整体路径更优。

与其它航迹规划算法相比，PSO算法[4]的突出优点是具有较强的鲁棒性，对种群大小敏感性不高，设计参数少，前期收敛速度快；缺点是后期收敛速度慢，容易早熟陷入局部最优解。为了克服PSO算法的缺点，许多研究者针对无人机航迹规划的PSO算法开展了研究工作，提出了一些改进方法。文献[5]在PSO算法中引入自适应灵敏度决策算子，克服了局部最优解和后期收敛速度慢的问题。文献[6]的改进方法是引入了空间精选投票机制找出解空间中每一个航迹点的最优位置。文献[7]采用人工势场法构建PSO算法的代价函数，克服局部最优解，并提高算法收敛速度。文献[8]采用模拟退火突跳概率策略对PSO算法的粒子位置更新方式进行了改进，能够增大全局搜索能力。文献[9]采用分层随机初始化与粒子偷懒流放策略改进PSO算法，加快了收敛效率。文献[10]引入蚁群算法的信息素加快PSO算法的收敛速度，并通过模糊处理控制航迹规划的输入量，防止系统陷入局部最优解。文献[11]设计了分段式惯性权重调整公式改进PSO算法，在保证算法搜索速度的同时提高了航迹规划解的精度。

尽管前人对无人机航迹规划的粒子群优化算法开展了较为深入的研究，但是对固定翼无人机飞行性能约束条件的研究还不够深入。小型固定翼无人机自身飞行性能的约束条件较为严苛，满足约束条件是保证无人机飞行安全性的基础。另外，航迹规划算法的主要问题在于算法计算复杂度、求解精度、搜索时间难以平衡；因此设计具有计算快、精度高、容错率大等特点的航迹规划算法是未来发展趋势[11]。文献[12]在无人艇航线规划中应用了量子粒子群优化(quantum particle swarm optimization，QPSO)算法，在QPSO算法中粒子不再有速度向量，在每次迭代中粒子不再受限于速度来更新个体位置，而是在整个空间里进行全面优化搜索最优解，提高了全局搜索能力。而且QPSO算法的设计参数只有1个，即收缩-扩张因子，与其它改进PSO算法相比在计算复杂度方面具有显著的优势。本文将QPSO算法应用到固定翼无人机的三维航迹规划中，克服传统的PSO算法的缺点，为固定翼无人机在复杂三维环境空间中执行任务提供了可靠保障。

1 航迹规划问题描述

1.1 规划环境建模

环境建模就是将环境中的各种物理信息转换为计算机算法能处理的数字模型，这是规划无人机飞行航迹的前提和基础。本文以固定翼无人机在山区环境中执行自然灾害(例如山体滑坡、泥石流、森林火灾等)勘察任务为背景进行研究。山区环境中存在着山峰、高压电线、树木等障碍物威胁，此外，在山峰附近还存在风切变区等恶劣气象威胁。以东北天坐标系作为惯性参考坐标系，采用圆锥体来近似模拟高耸的山峰，山区地形高度可用如下算法模拟：

(1)

式中：z0为基准地形高度；hm为第m个山峰的高度；M为山峰总数目；(xm,ym)为第m个山峰的中心轴在地面的坐标；xsm和ysm分别为第m个山峰的横向坡度和纵向坡度。

风切变区由圆柱体来近似表示，第m个风切变区在地面圆心的坐标为(xwm,ywm)，半径为rm。对于高压电线和树木等威胁，无人机通过自身最小飞行高度约束来规避，即无人机的最小飞行高度应比高压电线和树木的最大高度高出一定的距离。

1.2 无人机约束条件描述

前人对固定翼无人机的飞行性能约束条件研究不深入，固定翼无人机不具备旋翼式无人机的垂直起降、空中悬停、飞行灵活等性能，因此飞行中自身约束条件要比旋翼式无人机严格得多。本文重点分析以下几项性能约束条件。

1)最大航程

设无人机的最大航程为Lmax，算法规划出的航迹包括K段航迹段，第k段航迹段的长度为：Lk，k=1,2,…,K，则最大航程约束表示为：

(2)

2)最小惯性距离

最小惯性距离是指无人机突然变换飞行方向时，由于惯性作用需要按原方向飞行的最短距离。设最小惯性距离为Lmin，则最小惯性距离约束条件可以表示为：

Lk≥Lmin，k=1,2,…,K

(3)

3)最大水平转弯角

受本身硬件性能的限制，无人机在水平方向转弯时，转弯角度无法超过最大水平转弯角Δψmax，设第k段航迹段相比于第k-1段航迹段的水平转弯角为Δψk，则水平转弯角约束为：

|Δψk|≤ψmax，k=1,2,…,K

(4)

4)最大高低角

高低角是指无人机向上爬升或向下俯冲的角度，与水平转弯角类似，由于性能限制，无人机飞行中的高低角不能超过最大高低角θmax，设第k段航迹段与水平面的夹角为θk，则最大高低角约束为：

|θk|≤θmax，k=1,2,…,K

(5)

5)最大、最小飞行高度约束

无人机执行勘察任务需要在低空飞行，距离地面的高度不能太高。设定无人机距离地面的最大高度为Δhmax，一条航迹由D个航迹点组成，D是粒子的维度。第d(d=1,2,…,D)个航迹点的坐标值为(xd,yd,zd)，海拔高度为zd，而航迹点下面的地面海拔高度由式(1)求得，即

z1d=z1(xd,yd)

(6)

则最大飞行高度约束条件表示为：

zd≤z1d+ Δhmax，d=1,2,…,D

(7)

另外，无人机在山区环境中执行勘察任务，不仅要考虑地面高度，而且要考虑高压电线、树木等障碍物的高度，假设高压电线和树木的最大高度为：ht。为了保证无人机飞行安全性，再增加一定的安全高度差，以hsafe表示，则最小飞行高度约束条件表示为：

zd≥z1d+Δhmin，Δhmin=ht+hsafe

(8)

本文研究固定翼无人机的三维航迹规划问题，如果直接在三维环境空间中进行航迹规划，算法的计算量太大，耗时长。为了减小算法计算的复杂度，提高规划效率，对三维航迹规划问题的高度规划采用直接设定策略，即，设置各个航迹点的海拔高度介于最大、最小飞行高度之间，表达式为：

zd=z1+Δz，d=1,2,…,D

(9)

Δhmin<Δz<Δhmax

(10)

因此约束条件(5)自然满足，同时，将三维航迹规划问题简化为二维航迹规划问题，算法搜索过程是在二维平面内搜索候选航迹点，并且只需要检查其他4项约束条件是否满足要求即可，保证了本文算法简单高效。

2 量子粒子群优化算法

为了解决传统PSO算法的局部最优解问题，文献[13]提出了QPSO算法，以提高全局寻优能力。在经典力学中描述粒子的2个因素是位置矢量和速度矢量，它们决定了粒子的运动轨迹；但在量子力学中粒子为自由移动，并向局部吸引点pn倾斜，同时粒子的动能逐渐减小到0。在势阱模型中，波函数ψ用于表示粒子的状态。由于ψ的统计特性，在距离点pn较远的地方可能会出现一些粒子，这些粒子有机会找到更优的解的位置。

种群中的粒子数目为N，在第t次迭代时，第n个粒子的个体最优位置表示为：

Pn(t)=[Pn,1(t),Pn,2(t),…,Pn,D(t)]

(11)

种群的全局最优位置表示为：

Gn(t)=[Gn,1(t),Gn,2(t),…,Gn,D(t)]

(12)

第n个粒子的局部吸引点位置表示为：

Sn(t)=[Sn,1(t),Sn,2(t),…,Sn,D(t)]

(13)

Sn,d(t)=rPn,d(t)+(1-r)Gn,d(t)

(14)

式中：r是(0,1)之间的随机数。

在第t+1次迭代时，第n个粒子的位置进化方程表述为：

(15)

式中：α是收缩-扩张因子；μ是(0,1)之间的随机数；Cd(t)是种群所有个体最优位置的中心点，即，

(16)

在QPSO算法的式(15)中，当r≤0.5时，取“+”号；否则取“-”号。待设计参数为α，它的作用是协调迭代过程粒子的局部和全局的搜索性能。其值越小则局部寻优能力越强，全局寻优能力越弱；反之则全局寻优速度越强。文献[12]指出，α一般取为固定值或线性减小调节策略，但是，我们采用QPSO算法进行了无人机航迹规划的大量仿真尝试，由仿真结果对比发现，α取为固定值或线性减小的调节策略时规划效果并不太好，然而取为线性增大的调节策略时具有更强的寻优能力和规划效果，α的表达式如式(17)。

α=αmin+(αmax-αmin)·t/Tmax

(17)

式中：αmax和αmin分别为α的最大值和最小值；t为当前迭代次数；Tmax为最大迭代次数。

3 无人机三维航迹规划

采用QPSO算法开展固定翼无人机的三维航迹规划，其核心任务是建立代价函数(或称为适应度函数)的数学模型和有效地处理各项约束条件。代价函数是衡量一条航迹优劣的指标函数。综合前面分析的各种环境威胁、无人机约束条件等要素，建立代价函数时需要考虑威胁代价、航迹长度代价和约束条件代价等指标，表达式如下：

JUAV=w1J1+w2J2+w3J3

(18)

式中：J1表示航迹长度代价；J2表示威胁代价；J3表示约束条件代价；w1，w2和w3分别为这3项代价的权重，w1+w2+w3=1。一条航迹的代价函数值越小，表明这条航迹越优。

根据前面的最大航程约束条件描述，可以建立如下的航迹长度代价函数：

J1=LUAV

(19)

考虑到三维环境空间中的山峰、风切变区等威胁源的影响，规划航迹到各个威胁源的距离越远越好，从而无人机的飞行安全性越高。山峰威胁代价函数设计为：

(20)

(21)

综合起来，威胁代价函数设计为：

J2=k21J21+k22J22

(22)

式中：k21和k22为比例系数。

下面建立无人机约束条件的代价函数。为了简便起见，采用惩罚代价来设计代价函数。根据前面的最大航程约束条件描述，最大航程约束的代价函数设计为：

(23)

式中：J31为最大航程约束代价；C0为惩罚代价常数，不妨取较大的正数。

设最小惯性距离约束代价为J32，最大水平转弯角约束代价为J33，最大高低角约束代价为J34。它们都设计为式(23)的形式。综合起来，约束条件代价函数设计为：

J3=J31+J32+J33+J34

(24)

以代价函数式(18)作为QPSO算法的指标函数，通过迭代搜索寻优，最终找到的全局最优解就是规划出的最优参考航迹。

4 仿真校验

采用MATLAB R2010b软件编程构建无人机三维航迹规划仿真模型，进行仿真实验检验QPSO算法的有效性。设置山区环境为100km*100km*3km的空间区域，基准地形高度为z0=0.05km，无人机的起始点S坐标为(0,0,0.06)，第1个任务点T1坐标为(47,80,1.1)，第2个任务点T2坐标为(84,24,1.0)。无人机从起始点飞行到T1点上空执行自然灾害勘察任务，然后再飞行到T2点上空勘察，最后返回起始点。本文重点研究航迹规划问题，为了简便起见，将上述各段航迹分别进行规划，即，第1段规划航迹为：S→T1；第2段规划航迹为：T1→T2；第3段规划航迹为：T2→S。无人机在T1点上空盘旋几周执行勘察任务，并完成转弯，然后飞行到T2点上空勘察。盘旋勘察工作这里不进行研究，本文工作是采用QPSO算法开展无人机三维航迹规划。在山区环境中设置了8座山峰和8个风切变区。

利用式(1)计算出x∈[0,100]，y∈[0,100]范围内的山区地形高度z1。设置固定翼无人机的约束条件分别为：Lmax=500km，Lmin=1.0km，Δψmax=60°，θmax=60°，Δhmax=0.5km，ht=0.02km，hsafe=0.05km。设置无人机的实时航迹高度高于其下方地形高度0.15km，满足最大、最小飞行高度约束条件。应用仿真试凑法进行反复尝试，确定算法参数如下：αmax=1.0，αmin=0.6，N=300，D=25，Tmax=100，w1=0.3，w2=0.3，w3=0.4，k21=30，k22=30，C0=300。为了与传统PSO算法进行对比，也采用了传统PSO算法进行无人机航迹规划仿真实验。在传统PSO算法中与α对应的参数为：惯性权重w、学习因子c1和c2，都为常数[1]。应用仿真试凑法确定算法参数如下：w=0.5，c1=2.0，c2=2.0，N=300，D=25，Tmax=100，w1=0.3，w2=0.3，w3=0.4，k21=30，k22=30，C0=300。采用蒙特卡洛法进行100次仿真实验，对仿真结果进行统计分析，求出3段航迹的代价的平均值，两种算法的代价对比如表1所示。

表1 两种算法的代价对比

由表1可以看出，对于3段规划航迹，本文设计的QPSO算法都比传统PSO算法获得了更小的代价值，表明了本文算法具有更高的全局搜索能力和搜索精度。下面给出最后一次的仿真结果，采用QPSO算法的无人机3段航迹及其代价值收敛曲线如图1所示，基于传统PSO算法的无人机航迹及其代价值收敛曲线如图2所示。

图1 采用QPSO算法的无人机航迹规划结果

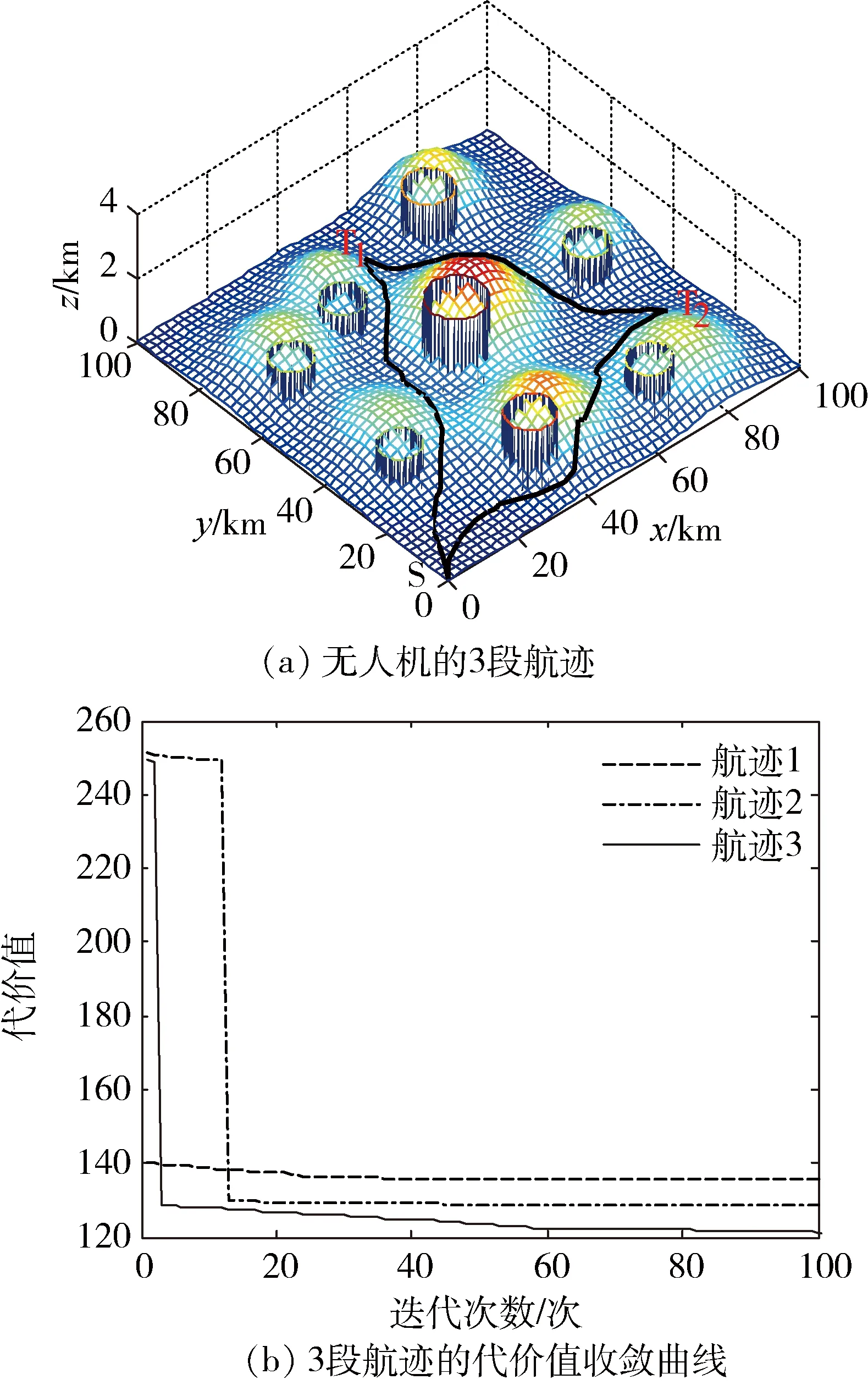
图2 采用传统PSO算法的无人机航迹规划结果

4 结论

针对传统粒子群优化算法的易陷入局部最优解的缺点，本文采用量子粒子群优化算法解决固定翼无人机的三维航迹规划问题。详细分析了固定翼无人机的飞行性能约束条件。为了减小算法计算复杂度，提高规划效率，对三维航迹规划问题的高度规划采用了直接设定策略，从而将三维航迹规划问题简化为二维航迹规划问题。设计了收缩-扩张因子的线性增大调节策略、代价函数和航迹规划流程。为了检验量子粒子群优化算法的有效性，分别采用量子粒子群优化算法和传统的粒子群优化算法开展了无人机三维航迹规划仿真实验。仿真结果对比表明，本文设计的量子粒子群优化算法具有更高的全局搜索能力和搜索精度。