结合坐标变换的GM(1，1)模型及其变形预测应用

邱 利 军，张 波，周 占 学，张 京 奎

(1.河北建筑工程学院，河北 张家口 075000； 2.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000； 3.中国电子科技集团公司第54 研究所，河北 石家庄 0500813)

建筑物在施工建设过程中需要进行变形监测以观测其变形状态，同时确保其建设期间的安全，该项工作一般会延续至运营期间。在获得变形数据后，变形分析则显得尤为重要，而变形预测是变形分析的一项重要内容。精确的变形预测能够对后期变形量有准确的判断，并对可能发生的危险情况提前制定应对策略，以避免危险发生，从而达到降低损失的目的。常用的变形预测方法有回归分析法、时间序列分析法、灰色系统分析模型、神经网络模型等[1]。由我国邓聚龙教授所提出的GM(1，1)模型是灰色系统理论的基本模型[2]，其“小样本、贫信息”的建模特点能够做到建模预测的及时性。GM(1，1)模型在变形数据预测领域的应用研究与实践已经展开，并取得了诸多成果。其中，王艳艳[3]等、王朝阳[4]等结合工程实践分别针对传统均值GM(1，1)模型和新陈代谢GM(1，1)模型进行了应用研究。而由于模型建模存在优势建模维数，因此选取合适的等维或非等维优势建模维数对GM(1，1)模型进行改进能够提高建模预测的精度[5-7]；同时，由于传统GM(1，1)模型在建模机理上存在固有缺陷，因此，从初始值选取[8-9]、背景值重构[10-11]、光滑比优化等[12-14]一个或多个方面对其进行改进，能够提高预测精度。文建华[15]等采用函数对原始数据进行数据重构以剔除原数据中干扰因子；蔡小辉[16]等通过分解原始序列以提取单调序列，从而建立GM(1，1)模型进行变形预测；高宁[17]等引入半参数理论构建滑坡半参数GM(1，1)模型；胡华[18]等则以摩擦学理论为基础推导出边坡演化的非线性动力学模型，结合灰色系统理论构建了以速率为参量的GM(1，1)模型并应用于滑坡时间预测。而针对数据序列波动频繁等复杂数据预测问题，许多学者采用人工神经网络模型、灰色马尔科夫模型、自回归模型、Kalman滤波等与GM(1，1)模型组合进行组合预测研究，取得了较好的效果[19-20]。

但是在传统GM(1，1)模型、原始数据变换改进的GM(1，1)模型[21-23]以及基于建模机理缺陷改进的GM(1，1)模型中，其本质依然是指数函数预测，无论拟合精度多高，建模序列的一次累加序列和拟合函数序列在后期依然出现相近、相交或相离的趋势，并不重合[24-26]。基于这种情况，提出采用平面坐标变换的方法对模型进行了改进，并以实测变形数据进行预测验证。

1 结合坐标变换的GM(1，1)模型

设原始数据序列为非负离散序列X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))，X(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))是X(0)的1-AGO序列，那么X(1)的紧邻均值生成序列是Z(1)=(z(1)(2)，z(1)(3)，…，z(1)(n))。则GM(1，1)模型为

x(0)(k)+az(1)(k)=b

(1)

(2)

式(2) 称为式(1) 的白化方程。

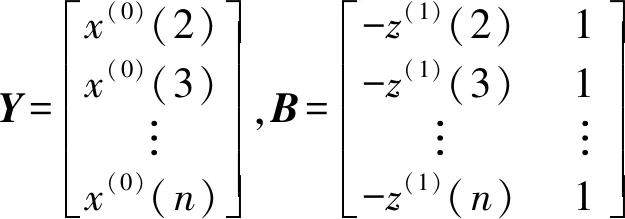
用最小二乘法可求解得：

(3)

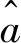
(4)

式(4) 即为X(1)序列预测公式；若k+1≤n，即为拟合值；若k+1>n，即为预测值。

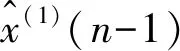
(5)

若Δ>0，公式(4) 的计算值则下移，反之，则上移。平移后公式为

(6)

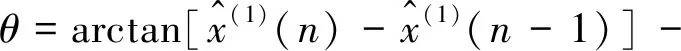
arctan[x(1)(n)-x(1)(n-1)]

(7)

若θ>0，则平移后进行顺时针旋转；若θ<0，则在平移后进行逆时针旋转。

(3) 计算旋转后坐标。坐标系中任一点(x，y)可绕点(x0，y0)旋转θ角，得到新的坐标点(x′，y′)，其对应转换公式为

(8)

(9)

注意，若n+i>xn+m，则以对应的xn+m-1和xn+m两点连线延长线上的值为预测值。

对得到的预测序列累减还原，即可得到建模序列X(0)的m期预测序列。若序列建模前进行了预处理，则需要进行反向还原处理。

模型原理如图1所示，建模序列与拟合序列对应的第n个值以及第n-1个值所构成折线段趋势可能是相近(图1中n=5，n-1=4)、相交(图1中n=6，n-1=5)、相离(图1中n=7，n-1=6)的趋势，平移使得第n个值重合(图中采用n=6示意)，计算夹角并进行绕点旋转的坐标变换，然后取横轴为定值时旋转后折线上对应的纵坐标值作为一次累加序列预测值(图1中虚线与旋转后折线交点)。由图1可知，旋转变换会导致拟合序列部分数据误差较大，但由于建模序列为已知序列，仅考虑预测阶段序列，则改进方法达到了提高预测序列精度的目的。需要说明的是：绕点旋转不改变旋转点至基准点(已知一次累加序列最后一项)的长度，图中长度不等是由于纵横坐标轴比例尺不同所致。

图1 模型原理示意Fig.1 Schematic diagram of model principle

2 工程实例

采用大坝沉降观测数据和基坑沉降观测数据进行算法验证，算法采用C#编程实现，中间变量均采用双精度(double)型数据，最后数据四舍五入取至小数点后两位。并采用4种不同模型对原始数据序列进行建模预测，以进行比较分析。所采用的模型如下：模型1，均值GM(1，1)模型；模型2，结合坐标变换的均值GM(1，1)模型；模型3，ln(x+c)预处理后均值GM(1，1)模型；模型4，ln(x+c)预处理后再结合坐标变换的GM(1，1)模型。

实例1：取陆浑水库大坝坝顶P29测点11期沉降变形观测数据[5-6]，采用上述4种模型，以前9期数据作为原始序列进行建模，预测第10期和第11期数据。前9期实测建模数据序列如表1所列，后两期的预测数据与实测值及原文献方法的预测值如表2所列；后两期预测数据与原文献方法预测值的相对误差如表3所列。

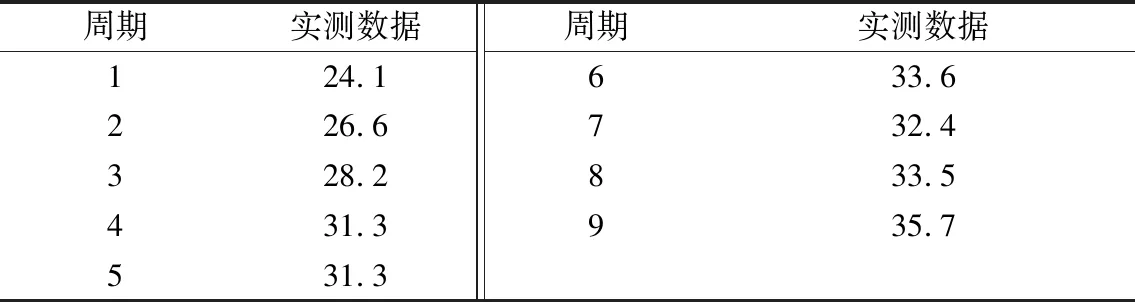
表1 实测建模数据序列值Tab.1 Sequence value of measured modeling data mm

表2 不同模型的预测值Tab.2 The predicted values by different models mm

由表2和表3可知：模型4的预测结果最好，其相对误差最小，仅为0.11%；模型2的预测精度次之，相对误差最大为0.16%；将模型1和模型2～4分别比较，可知坐标变换对模型预测精度有明显提高。4种模型自第9～11期的预测(第9期已知)与实测曲线如图2所示。

表3 不同模型预测值的相对误差Tab.3 The relative error of models’ predicted values %

图2 不同模型建模预测曲线Fig.2 The predicted curves by different models

由图2可知，坐标变换过程是对模型1以及模型3预测值沿纵向向实测值的趋近和校正。

实例2：采用某基坑监测单个沉降观测点10期实测累计沉降数据[10]，利用上述4种模型，以前7期数据作为原始序列进行建模，预测第8～10期数据。前7期实测建模数据序列如表4所列，后3期预测数据与实测值如表5所示；后3期预测数据的相对误差如表6所示。

表4 某基坑实测建模数据序列值Tab.4 Sequence value of measured modeling data of a pit mm

表5 算例2不同模型的预测值Tab.5 The predicted values of case 2 by different models mm

分析表5和表6可知：模型4的预测结果最好，其相对误差均在0.4%以下；模型3的预测精度次之，其相对误差在0.5%～3.5%之间；分别比较模型1和模型2～4，可知坐标变换对模型预测精度提高明显。4种模型自第7期至第10期预测(第7期为已知值)结果与实测曲线对比见图3。

由图3可明显发现：坐标变换过程虽然是对模型1及模型3预测值沿纵向向实测值的趋近和校正，但是可能出现图3中模型1与模型2的情况，即变换前后两条预测曲线分别位于实测曲线上方和下方，其原因在于以前期实测值与拟合值之间的夹角代替后期待测值与预测值之间的夹角误差较大，导致校正过大。

表6 不同模型预测值的相对误差Tab.6 The relative error of models’ predicted values %

图3 算例2不同模型建模预测曲线Fig.3 The predicted curve of case 2 by different models

综合实例1及实例2可知，坐标变换后模型能够提高原模型精度，其与ln(x+c)变换提高精度的原理不同，两者对精度提高的大小取决于原始已知序列，并不能单独认为某项改进较另一改进预测精度高，同时采用ln(x+c)变换和坐标变换的方法，会得到比单一改进方法更高的预测精度。而ln(x+c)变换与坐标变换组合改进模型的最终精度取决于变量c能否取到较佳的估值。上述实例1所取c为40，而实例2所取c值为5.7。

3 结 论

本文针对传统GM(1，1)模型的一次累加序列预测函数与实测累加序列存在趋势偏差这一情况，提出采用平面坐标变换的方式对模型进行改进，以此来提高预测精度。同时以实测变形监测数据来验证改进模型的精度，并对多种不同模型预测结果进行对比分析，得到以下结论：① 坐标变换的改进模型精度较高，适用于短期变形预测，具有一定的工程实践应用价值；② 该方法对本质为指数函数拟合预测的GM(1，1)系列模型具有适用性；③ 该方法依然需要满足GM(1，1)模型建模序列要求，即序列近似指数增长，存在适用条件限制，对不满足建模条件的序列需要对原始序列进行预处理；④ 由于本质为指数函数预测，因此在处理频繁波动等复杂数据情况下难以独自进行，需要与其它模型进行组合处理；⑤ 坐标旋转变换的方法也可以向其它单一趋势外推预测模型推广。