土石混合料阈值细粒含量的确定

周 雨 奇，王 涛，刘 斯 宏

(河海大学 水利水电学院，江苏 南京 210024)

无黏性土石混合料是由粗粒岩石和细粒土颗粒组成的混合料，这种混合材料一般是经历过一定的地质作用形成的，既不是均质土体，也不是碎裂岩体，而是一种介于均质土体与碎裂岩体之间的混合体，如卵砾石层、冰碛土、火山角砾岩、崩积层等[1-2]。土石混合料作为一种填筑材料在自然界中分布广泛，被普遍用于水利、铁路、公路等基础工程建设之中[3]。

无黏性土石混合料中的细粒(土粒)含量能够很大程度影响其物理力学性质：当土粒含量较少时，石颗粒承担主要的骨架作用，土石混合料的力学性质主要由石颗粒的性质决定；而随着土粒含量逐渐增多，土石混合料的力学性质主要由土颗粒决定[4]。在石粒为骨架到土粒为骨架的转变中，存在一个土粒含量作为分界，称为阈值细粒含量fcth[5]。当土粒含量fcfcth时混合料为类土颗粒骨架。fcth是区分粗粒岩石和细粒土颗粒接触状态及力学特性的重要参数，因此fcth值是研究土石混合料力学特性需要重点关注的一个问题[6]。

许多学者对阈值细粒含量fcth的预测方法及影响因素做了研究。Thevanayagam等[7]提出用粗细颗粒粒径比Rd确定阈值细粒含量的经验公式法。Rahman等[8]基于试验结果提出了基于有效粒径比的阈值细粒含量计算公式，并根据二元聚集模型对理论公式进行简化，得出基于纯砂砾土孔隙比和纯土粒孔隙比的阈值细粒含量经验公式。朱建群等[9]在假设砂-粉二元结构的前提下，探究了分形理论在分析临界细粒含量中的作用。Cho等[10]试验发现，经验公式更适用于次圆状和圆状颗粒，而当颗粒形状越接近角状，其emax和emin越大，需要更多粉粒充填孔隙，使计算得到的fcth偏小。Rahman等[11]分析发现，当颗粒粒径相差较小时，土石混合料不满足二元聚集模型的要求，粉粒的增加将增大砂粒间的孔隙，造成混合料体积增大。上述阈值细粒含量的预测公式都是基于二元聚集模型假设，由于没有考虑土石混合料中土与石的级配的影响，导致预测结果与试验值有出入。为此本文提出一种能够考虑土石混合料级配的阈值细粒含量预测模型。

本文开展了系列室内压实试验，探究了典型级配参数(石料不均匀系数Cuc、土料不均匀系数Cuf和土石粒径比Rd)对阈值细粒含量的影响规律。然后基于试验结果建立了考虑土、石级配影响的土石混合料堆积模型，该模型可用于确定土石混合料阈值细粒含量。

1 土石混合料压实试验

1.1 试验材料与方法

本文所用试样取自江苏某抽水蓄能电站料场，土料及石料均为微风化白云岩，其属于同一岩性，比重相同为2.62。取5 mm作为土石粒径的临界点，并认为d>5 mm颗粒为石颗粒，d<5 mm为土颗粒，试样的最大粒径为20 mm。土石混合料级配曲线示于图1。

图1 土石混合料级配曲线Fig.1 Gradation curve of earth-rock mixture

本次试验分别探究了石料不均匀系数Cuc、土料不均匀系数Cuf、土石平均粒径比Rd三种因素对阈值孔隙比的影响，具体土石级配参数列于表1(T2、T5、T8为相同级配)。在含水率为0的条件下，对细粒含量分别为0，10%，30%，50%，60%，70%及100%的土石混合料分别进行振动压实试验，共计7×7=49个试样。

1.2 试验结果与分析

为探究土料不均匀系数、石料不均匀系数及土石粒径比对土石混合料最小孔隙比的影响，通过分别控制其中两个因素相同，改变另一因素设计试样级配，分析3种影响因素对土石混合料阈值孔隙比的影响。

表1 试验设计中3种影响因素取值Tab.1 Designed values of three gradation parameters

1.2.1石料不均匀系数Cuc的影响

如图2所示，当控制Cuf=7.01和Rd=5.46不变，可以探究石料不均匀系数Cuc对土石混合料阈值细粒含量的影响规律。对于不同的石料不均匀系数Cuc，随着土粒含量增大，土石混合料压实孔隙比均先减小后增加，转折点对应的土粒含量即为阈值细粒含量fcth，当土粒含量低于fcth时，土石混合料中以石料承担骨架，反之为土料承担骨架。

图2 不同石料不均匀系数下的土石混合料 最小压实孔隙比Fig.2 Minimum void ratio of soil-rock mixtures with different uniformity coefficients of rock grains

可见，随着石料不均匀系数Cuc增大，土石混合料阈值细粒含量降低。这是因为随着Cuc增大，石颗粒之间孔隙体积减小，即需要更少的土颗粒去填满石颗粒之间的孔隙，因此fcth降低。

1.2.2土料不均匀系数Cuf的影响

不过笔者认为，尽管调解有其风险，如果完全否认法庭口译员扮演文化调解者的可能性并不利于沟通障碍的消除。重要的是应该提高各方对于文化调解者角色的认识，并对恰当的文化调解策略达成一致。

如图3所示：控制Cuc=2.36和Rd=5.46不变，可以探究土料不均匀系数Cuf对土石混合料阈值细粒含量的影响规律。图3给出了不同土料不均匀系数Cuf下土石混合料的最小孔隙比，可见fcth随着Cuf的增加而减小，这是由于对相同的土料平均粒径而言，Cuf增加意味着土料中粒径较大的土颗粒变多，因此需要更少的土颗粒去填满石颗粒之间的孔隙。

图3 不同土料不均匀系数下的土石混合料 最小压实孔隙比Fig.3 Minimum void ratio of soil-rock mixtures under different uniformity coefficients of soil grains

1.2.3土石平均粒径比Rd的影响

控制Cuc=2.36和Cuf=7.01不变，可以探究土石颗粒粒径比Rd对土石混合料阈值细粒含量的影响规律。由图4可知，当Rd从3.60增大至6.43，fcth逐渐增大，这是因为随着Rd增加，石颗粒间孔隙体积与土颗粒体积的比值增大，因此允许更多的土颗粒填充石颗粒间的孔隙。

图4 不同土石平均粒径比下的土石混合料 最小压实孔隙比Fig.4 Minimum void ratio of soil-rock mixtures under different ratios of grain sizes between soil grains and rock grains

2 考虑土石级配的土石混合料堆积模型

2.1 现有堆积模型

Humphres提出了图表式的经验公式用以预测土样的最大密度。Kezdi和Vallejo[14]基于大颗粒孔隙中恰好完全充满小颗粒这一理想状态推导了土样最小孔隙比与细粒含量关系式。为考虑堆积过程中土石颗粒间的相互扰动，Chang[15]针对砂-粉土混合料，提出了考虑颗粒间相互扰动的堆积模型：

eM=e1y1+e2y2-a12(1+e)y2

(1)

eM=e1y1+e2y2-b12e1y1

(2)

式中：eM为骨架孔隙比，e1为纯石最小孔隙比，e2为纯土最小孔隙比，y1和y2为石粒和土粒固相体积占比(y1+y2=1)；a12，b12是与粒径比d1/d2相关的参数：a12=(1-d2/d1)p，b12=(1-d2/d1)s，其中p=3.41，s=2.65[15]。

图5为前文压实试验数据与采用Vallejo和Chang的模型预测值的对比，发现由于没有考虑石料和土料的级配，Vallejo和Chang的模型对土石混合料的最小压实孔隙比的预测都存在较大误差。因此，本次研究在Chang提出的堆积模型框架下，考虑石料、土料级配的影响，用于土石混合料阈值细粒含量的预测。

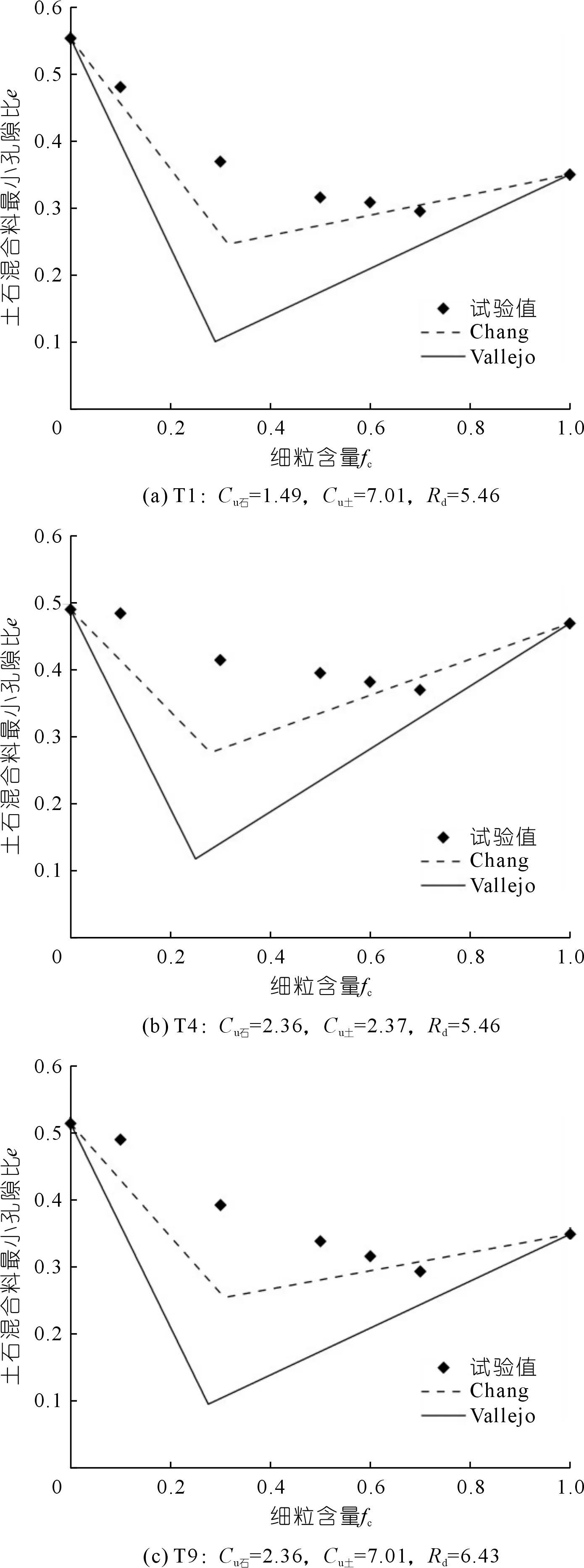
图5 Chang，Vallejo堆积模型预测值与试验值对比Fig.5 Comparison of experimental values and predicted values using Chang and Vallejo’s packing models

2.2 考虑土石级配的土石混合料堆积模型

土石混合料由两种粒径差距大的颗粒组成，即粗颗粒(石)和细颗粒(土)。如图6所示，这2种不同种类的颗粒体积表示为Vc和Vx(由于土、石颗粒的比重相同，其土石质量比就是体积比)。纯石颗粒料和纯土颗粒料的最小孔隙比分别为ec和ex，而模型的目标是预测不同细粒含量下土石混合料的最小孔隙比。

当假设石颗粒为主要组成材料时，石颗粒的体积为Vc，石颗粒之间的孔隙体积为Vck，未添加土颗粒状态下的纯石颗粒孔隙体积为Vk。把土颗粒添加到纯石颗粒体中，在极限情况下所有石颗粒间的孔隙都会被土颗粒填充而不会改变其结构，因此土颗粒的固相体积Vx在Vck中占有一定空间并且总体积保持不变。然而，这一理想的情况很难达到，由于土石颗粒间的相互扰动，石料的骨架会一定程度被撑开，因此总孔隙体积将增大，变化值为V*。

图6 土石混合料实际体积组成Fig.6 Actual volume proportions of soil-rock mixtures

图6中V*的计算根据Chang等人的理论，添加土颗粒所引起的石颗粒间孔隙体积变化与添加到混合料中的土颗粒数量成正比：

V*=kVx

(3)

式中：k是材料系数。

加入土颗粒后土石混合料的实际孔隙比e实为

(4)

(5)

(6)

由上述3式可得以石颗粒为骨架的实际孔隙比为

e实=ec(1-fc)+(1-k)fc

(7)

当土颗粒为骨架时，土颗粒的体积为Vx，孔隙体积为Vxk，同理当加入体积为Vc的石颗粒时，由于土石颗粒之间的扰动使总体积增加V*，其值与加入的石颗粒体积正相关，即：V*=mVc，则有：

(8)

Vxk=ex·Vx

(9)

联立式(5)、(8)、(9)，可得加入石颗粒后土石混合料实际孔隙比为

e实=ex·fc+(m-1)(1-fc)

(10)

联立式(7)与式(10)，可以得出从石颗粒骨架到土颗粒为骨架的转折点，即阈值孔隙比ecth，其对应的即为土石混合料的最小孔隙比：

(11)

式中：m，k均为与土石级配有关的材料参数。

只要根据试验算出系数m、k，并测得纯石料和纯土料的孔隙率，即可预测该种材料土石混合料的阈值细粒含量及对应最小孔隙率。为了更好地控制系数取值，将m、k进行简化。由于以石颗粒为骨架和以土颗粒为骨架的实际孔隙率线为两条相交直线AA0交BB0于点P，且其上限斜率为K0=ex-ec，根据几何约束两直线在AB线以下，如图7所示，推导出：0≤k≤1-ex，0≤m≤1+ec。假设2个新符号值在0～1。

(12)

(13)

图7 由土石颗粒实际孔隙比计算阈值细粒含量Fig.7 Threshold fine content diagram for calculating the actual void ratio of coarse and fine particles

根据压实试验结果，k0、m0与土料不均匀系数Cuf及石料不均匀系数Cuc呈负相关，与土石平均粒径比Rd呈正相关，将式(14)、(15)代入试验结果进行线性拟合得：

(14)

(15)

图8(a)、(b)分别为采用式(14)、(15)计算的k0、m0值及其试验值。由图可知，采用式(14)和式(15)能较好地拟合k0、m0。

线性拟合可得：a=b=d=f=1，c=e=0.5。

图8 土石级配相关材料系数拟合示意Fig.8 Fitting diagram of material coefficients related to soil and rock gradation

2.3 模型验证

将表1中9组不用级配的土石混合料用2.2节中考虑土石级配的土石混合料堆积模型进行预测，发现试验值与预测值吻合较好，如图9所示。

图9 考虑土石级配的堆积模型预测值与试验值对比Fig.9 Contrast chart of predicted value and experimental value of accumulation model considering soil and rock gradation

为进一步验证所提出的考虑土石级配土石混合料堆积模型的有效性，重新设计了一组级配的土石混合料并开展了压实试验，试验过程同上。试验用土石混合料级配曲线如图10所示。用于验证模型的土石混合料试验最大粒径为40 mm，Cuc=2.57，Cuf=7.32，Rd=9.38。图11给出了试验土石混合料不同土粒含量下的最小孔隙比的试验值与采用本文提出的土石混合料堆积模型预测值，可以看出试验值与预测值吻合较好，验证了考虑土石级配影响的堆积模型的有效性。

图10 验证试验纯土料与纯石料级配曲线Fig.10 Pure soil and pure stone gradation curve used in verification test

图11 不同土粒含量土石混合料的压实试验值及 模型预测值对比Fig.11 Comparison of experimental and predicted void ratio of soil and rock mixtures with different fine contents

3 结 论

本文开展了系列压实试验，基于压实试验结果，提出了一种可以考虑土与石级配的堆积模型，该模型可以较好地预测土石混合料的阈值细粒含量，得到的主要结论如下。

(1) 土石混合料阈值细粒含量fcth与石料不均匀系数Cuc、土料不均匀系数Cuf呈负相关，与土石粒径比Rd呈正相关。

(2) 若不考虑土石级配的影响，常规堆积模型对土石混合料堆积孔隙比与阈值细粒含量预测偏差较大。这是因为颗粒堆积过程中会产生相互扰动，而干扰程度又与土石级配相关。本文建立的考虑土石级配的堆积模型可以较好地预测土石混合料的阈值细粒含量。