溢洪道水流的二维有限体积法数值模拟

陈 松

(水利部新疆维吾尔自治区水利水电勘测设计研究院， 乌鲁木齐 830000)

1 概 述

溢洪道和其他泄洪建筑物设计的主要目的是安全地将洪水从大坝输送到下游河道，并防止大坝漫顶，特定类型溢洪道的选择和设计基于项目的特定目的、水文、泄洪要求、地形、地质、大坝安全和项目经济。由于提供高效输送水力和结构坚固的溢洪道对大坝的安全以及下游河流的生命和财产非常重要，因此水力模型被广泛用于解释水力现象的特性[1]。在综合考虑泄流能力、压力、水面线、消能布置等水力设计因素的情况下，对溢洪道进行水力高效设计，而且溢洪道宽度对大坝的经济分析和安全运行起着重要作用。目前，世界范围内大坝安全的主要问题是提供足够的溢洪道泄洪容量，但许多水坝设计和建造于20世纪60和70年代，水文信息有限。当时设计的许多水坝的溢洪道容量不足，可能会遇到潜在的问题，如在洪水条件增加的情况下，溢洪道顶部产生过大的负压，从而威胁大坝安全，因此溢洪道水动力学知识对溢洪道的安全设计具有重要意义[2]。本文针对溢洪道水流的流体力学问题，借助于数值模型，对溢洪道的流速分布、压力分布和流量特性进行模拟研究。

2 溢洪道过流特性

传统的溢洪道又称为反弧型溢洪道，主要由4部分组成：进水段、控制段、泄槽和消能防冲段。在坝顶上游，水流处于亚临界流状态(或逐渐变化的)；在坝顶之后，由于溢洪道为陡峭斜坡面，使得水流由亚临界状态变为超临界状态。溢洪道水流本质上是具有明显曲率且快速变化的水流，在顶部的水流中同时发生两个现象：沿剖面形成湍流边界层并且逐渐增厚，以及主流速度的逐渐增加和深度的逐渐减小。

溢洪道泄洪时由于斜坡面陡峭，水流流速过高，从而产生水流掺气。由于夹带空气而导致的流动膨胀增加了自由表面，从而间接影响设置侧壁高度和选择径向门的耳轴高度。对于溢洪道水流，垂直加速度非常重要，流速和压力会沿水流方向以及垂直方向变化。溢洪道水流基本上是在顶部附近快速变化的水流，在垂直方向上流线明显弯曲。由于溢洪道实体表面的曲线性质以及坝顶下游的陡坡，与实体边界的抗剪强度相比，垂直加速度在流动中起主导作用。

3 溢洪道水流数值模拟

利用高性能计算机和更高效的CFD(computational fluid dynamics)程序，可以在合理的时间和成本内对水工结构的性能进行数值研究。以往研究人员大多采用有限差分法模拟溢洪道水流。由于有限差分法对曲线体几何的适用性较弱，它在任意曲线体边界的重力驱动自由表面流动中的应用受到很大限制。而有限体积法、有限元法、边界元法等对曲面实体边界具有良好的适应性，得到了广泛的应用。在高速可压缩流动模拟中，守恒对于准确捕捉冲击波和其他流动不连续性是非常重要的，也是有限体积法的优点[3-5]。

本文基于空间弱可压缩流动方程，建立溢洪道绕流的二维有限体积法数值模拟模型。对于在垂直方向上变化迅速且在横向(如溢洪道上的水流)上显示出可忽略的水流变化进行建模，可以使用二维垂直模型。该模型的简化形式可作为一个宽度平均模型。

3.1 控制方程

自然界中典型的自由表面流具有较大的雷诺兹数，其特征是大尺度湍流混合。这些流动的马赫数很小，通常被视为不可压缩流动。在快速变化的条件下，一阶压缩性是不可忽略的。实际上，流体是可压缩的，压力总是与密度有关。因此，即使对于所谓的不可压缩流型，也可以使用可压缩形式的方程。为了使问题更易于数值求解，引入可压缩性。Song和Yuan发展了适用于小马赫数和大雷诺数实际流动的弱可压缩流体力学方程[6]。

对于包括瞬变流在内的一般马赫数流，其连续性方程为：

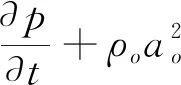
(1)

运动方程可以写成：

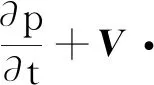
(2)

式中：p为压力，kPa；ρo为流体密度，kg/m3，ao为声速，m/s；V为速度矢量，m/s。

在上述方程中，τij是剪应力张量，假设重力作用于Y方向。满足式(1)和式(2)的流动称为弱可压缩流动。忽略运动方程式(2)中的黏性项，得到的运动方程称为欧拉方程：

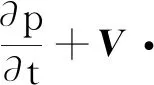
(3)

3.2 有限体积法(FVM)求解

针对溢洪道绕流问题，建立基于显式有限体积法(FVM)的数学模型。为了应用FVM格式，首先可以方便地重新编写控制方程式(1)和式(3)，其保守形式如下：

(4)

其中：G为流量变量(p，u，v)；F为流量矢量。

F=iE1+jE2

(5)

G=[puv]T

(6)

(7)

(8)

方程式(4)可以在任意有限体积上积分，应用散度定理，将体积积分转化为曲面积分。把它平均到现有的体积：

(9)

其中：G为G的体积平均值，m3；V为体积，m3；n为单位法向量；s为控制体积的表面积，m2。

方程式(9)由两步显式预测-校正方案求解。由于这是一种显式方法，计算时间步长必须基于数值稳定性考虑。

(10)

其中：s为控制体积的表面积，m2。在满足方程式(10)条件的整个区域上，计算的Δt的最小值作为计算时间步长。

在此基础上，建立溢洪道水流动力学数值模型。在所建立的模型中，从给定的初始条件出发，求解下一步所有网格点的速度和压力控制方程，计算新的自由曲面，生成新的网格系统，根据显式时间推进法计算每一时间步的流量，直至得到稳态解。

4 模型应用

本文以某拦洪坝溢洪道为例，利用所建立的数值模型对其进行水动力模拟。溢洪道设计洪水流量为55 m3/s。数值模型中模拟的部分原型包括：部分水库(长58.61 m，深39.144 m)；上游溢洪道坝顶剖面长8.61 m，下游反弧坝顶剖面长27.862 m。溢洪道部分的反弧坝顶剖面考虑到下游切点。

4.1 溢洪道物理模型

大坝溢洪道的物理模型研究是以1∶50的几何相似比例建造的二维截面模型上进行的。为了观察溢洪道上游和下游的水流状况，包括消能工的性能，在玻璃水槽中复制了模型。一个完整的跨度和两边的两个半跨度被复制。沿跨距中心在溢洪道表面安装直径为5 mm的压力计，用于测量压力；流量测量采用1.5 m宽尖顶堰；水位测量采用最小计数为0.1 mm的指针式仪表，从而对溢洪道模型的泄流能力、溢洪道表面的压力和水面线进行水力模型研究，最后将数值模拟结果与大坝溢洪道的物理模型研究结果进行比较。通过物理模型研究，主要从使用功能方面对溢洪道结构进行优化设计，以保证工程的技术的可行性。

4.2 网格划分

建立贴体网格系统进行有限体积法建模。图1为网格系统，将流场离散为18 400(230×80=18 400)个四边形单元网格。

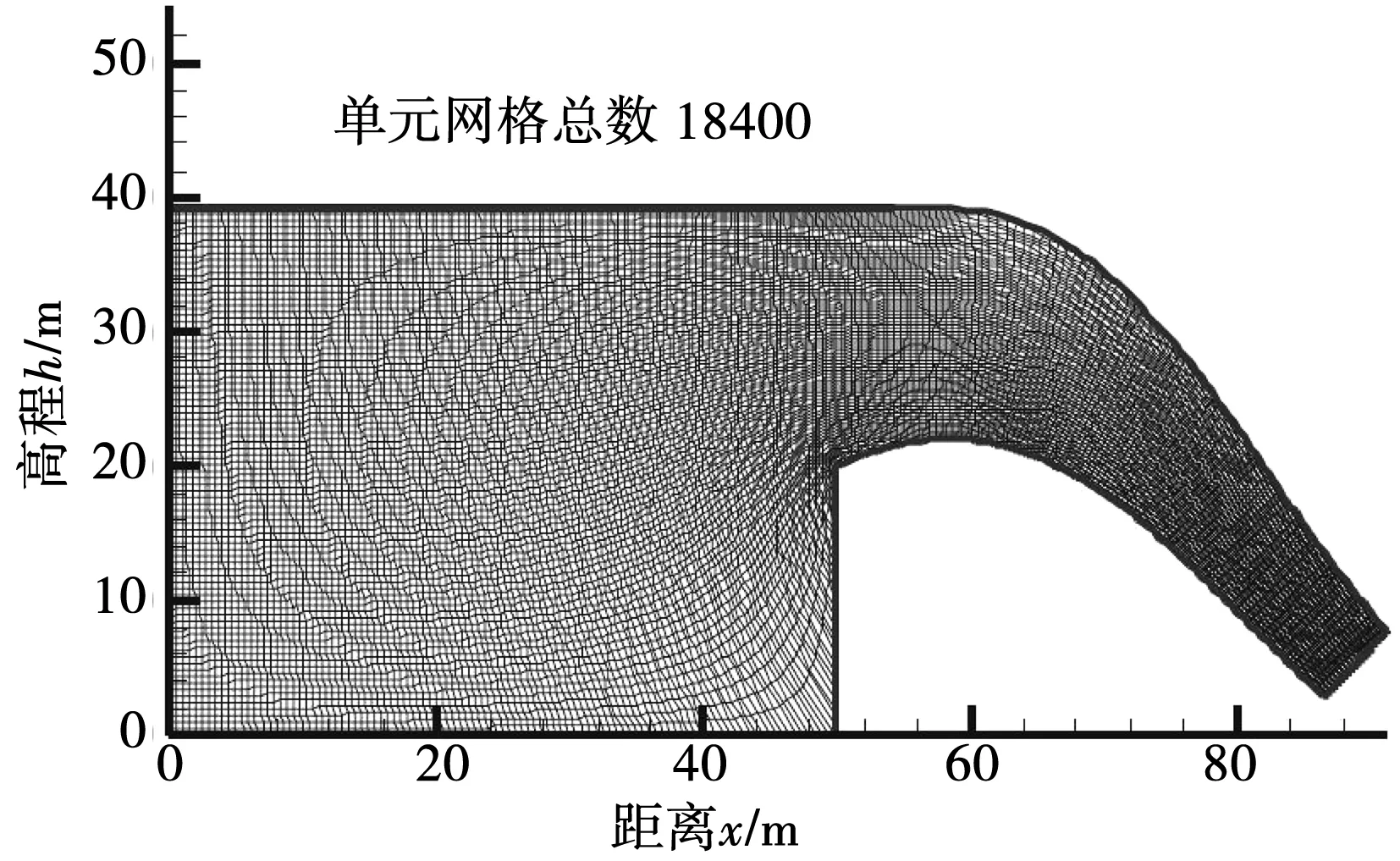
图1 溢洪道网格划分

4.3 边界和初始条件

4.3.1 溢洪道水流边界条件

边界条件指定了计算流域边界上的流动变量或其梯度。上游边界可以设置在水库断面上，在该断面上可知水库水位和来水流量。该段应远离溢洪道，以避免反射效应。基于速度分布的边界条件为：

u=uo(x0,y)

(11)

(12)

其中：x为流动方向；y为垂直方向；u、v为X和Y方向的速度分量；uo为上游边界X方向的速度分量，uo值由给定流量和水深确定。对于坝顶形状效应的研究，由于溢洪道下游斜坡的水流是超临界的，下游条件对上游水流没有影响。下游段可选择在流量充分发展的斜坡段上，以便假定速度和压力梯度为零。

固体边界条件有3种：完全滑移边界条件、部分滑移边界条件和无滑移边界条件。全滑移是指内网格处的切向速度等于固体表面上的切向速度；无滑移是指固体表面上的切向速度为零；对于部分滑移情况，应使用壁面函数。3种边界条件的选择取决于网格大小和边界层厚度的相对大小。在溢洪道和水库的固体边界处，采用全滑移条件。固体边界没有流动。

最难模拟的边界是时变自由面位置。影响自由表面的因素很多，如风应力、水与空气的热交换、表面张力应力等，通常采用运动学和动力学条件对自由表面进行模拟。运动条件是基于自由面是一个物质表面的观点，它的形式是：

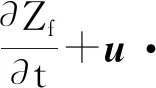
(13)

式中：Zf为沿法向的自由表面位移；u为沿流动方向的速度矢量；vf为垂直方向的自由表面速度，m/s。

该方程在迭代过程中，采用Mac-Cormack格式来修正新的自由面位置。忽略表面张力效应的动态边界条件是零应力条件。对于该模型，自由表面零应力的动态边界条件简化如下：

(14)

其中：n为垂直于自由曲面的单位向量。

4.3.2 溢洪道水流初始条件

溢洪道的初始流量为66 236 m3/s，其设计最大洪水流量为88 315 m3/s，相应的排放强度为143.99 m3/(s·m)。

4.4 结果和讨论

经过60 000个时间步，期间模拟结果不时地被检验，直到得到一个稳定的状态解。整个计算过程在1.0 GHz的处理器上进行了约12 h。并将物理模型上观测到的测压压力、水面线与模拟压力、水面线进行了比较，计算值与实验值吻合较好。图2为收敛后的压力分布(以等高线的形式)，同时也给出不同水位对应的压力水头。图3为解决方案收敛后固体表面上的压力分布，并与物理模型结果进行比较，结果显示模型观测压力与模拟计算压力结果相吻合。从图2和图3可以很明显地看出，在流动缓慢且稳定的水库部分，静水压力占主导地位。从图4和图5可以看出，在数值模型中上游坝顶剖面上形成一个温和的分离带，由于重力作用水流势能不断转化为动能，速度整体变大。由速度矢量图可以看出，溢洪道表面流速前半段增速较快，后半段增速较慢；而溢洪道底部水流前半段增速较慢，后半段增速较快，在溢洪道的后半段同一切面的流速相同。

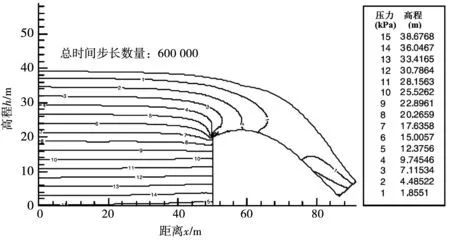
图2 溢洪道泄流压力分布

图3溢洪道面压力分布与物理模型计算结果的比较

图4 溢洪道流速分布

图5 溢洪道水流的流线形态

流量系数的计算值和实验值分别为0.72和0.69，流量系数计算值比实测值高4%。这可能是由于在宽均二维数值模型中，忽略了黏性项和紊流，假定了良好的直线流动，没有由于桥墩和桥台的端部收缩而造成的损失。数值模型显示了溢洪道坝顶附近的临界流段位置，其中无量纲水力参数弗劳德数是统一的，表明流态由次临界变为超临界流。

5 结 论

本文利用弱可压缩流动方程，建立了基于有限体积法的溢洪道坝顶断面水力特性数值模型。对选定溢洪道的流速分布、压力分布和泄流特性进行了估算，并与已有的物理模型资料进行了比较。主要结论如下：

1) 流量系数的计算值和实验值分别为0.72和0.69，比物理模型的实验值高4%。计算值较高的原因可能是忽略了黏性项和湍流，这通常会在水流中产生阻尼效应，并且在二维数值模型中没有由于桥墩和桥台引起的端部收缩造成的损失。

2) 从描绘压力等值线和流线的图中可以很明显看出，水库部分存在静水压力，溢洪道部分由于快速变化的加速流量而受到非静水压力的影响。

3) 数值模型显示了溢洪道顶部附近的临界流量段(弗劳德数=1)的位置，这与模型研究的既定事实非常吻合。

4) 上游坝顶剖面未能正确引导水流通过坝顶，因此在数值模型中，上游坝顶剖面上形成一个温和的分离区。

数值模拟结果与物理模型计算结果吻合较好，说明该模型在溢洪道实例水力模拟中的适用性，可将该模型应用于溢洪道泄洪水流特性的模拟，从而进一步加强大坝的安全运行。