梯形加糙渠道岸边流速系数的探讨
欧祖贤,聂会冲,刘克浩,王 瑾
(河北工程大学 水利水电学院,河北 邯郸 056000)
0 引 言
目前,在水利工程中最为广泛使用的流量测量方法是流速面积法,流速面积法就是流量等于过流断面平均流速与过流断面面积的乘积[1]。即在过流断面设置若干条测速垂线,测速垂线将过流断面划分为多个小断面,先求各个小断面流量,再求和即可求得过流断面流量。在求边坡垂线平均流速时,通常会再乘上岸边流速系数。
根据水文测验规范可知,岸边或死水边部分的平均流速等于自岸边或死水边起第一条垂线的平均流速乘以岸边流速系数α,计算公式为:
V1=αVm1
(1)
式中:V1为岸边或死水边部分的平均流速,m/s;Vm1为自岸边或死水边起第一条测速垂线的垂线平均流速,m/s。
岸边流速系数α的取值通常参考表1。

表1 岸边流速系数α的取值
表1中对岸边流速的选取较为粗略,未全面考虑螺类等生物附着于渠道边壁的影响,这会影响渠道流量测量精度。
1 不同岸边横向流速分布的岸边流速系数
1.1 横向流速分布为二次函数分布
假设横向流速分布趋于二次函数分布,则按抛物线曲线拟合推求岸边流速系数。假设横向分布图如图1所示。
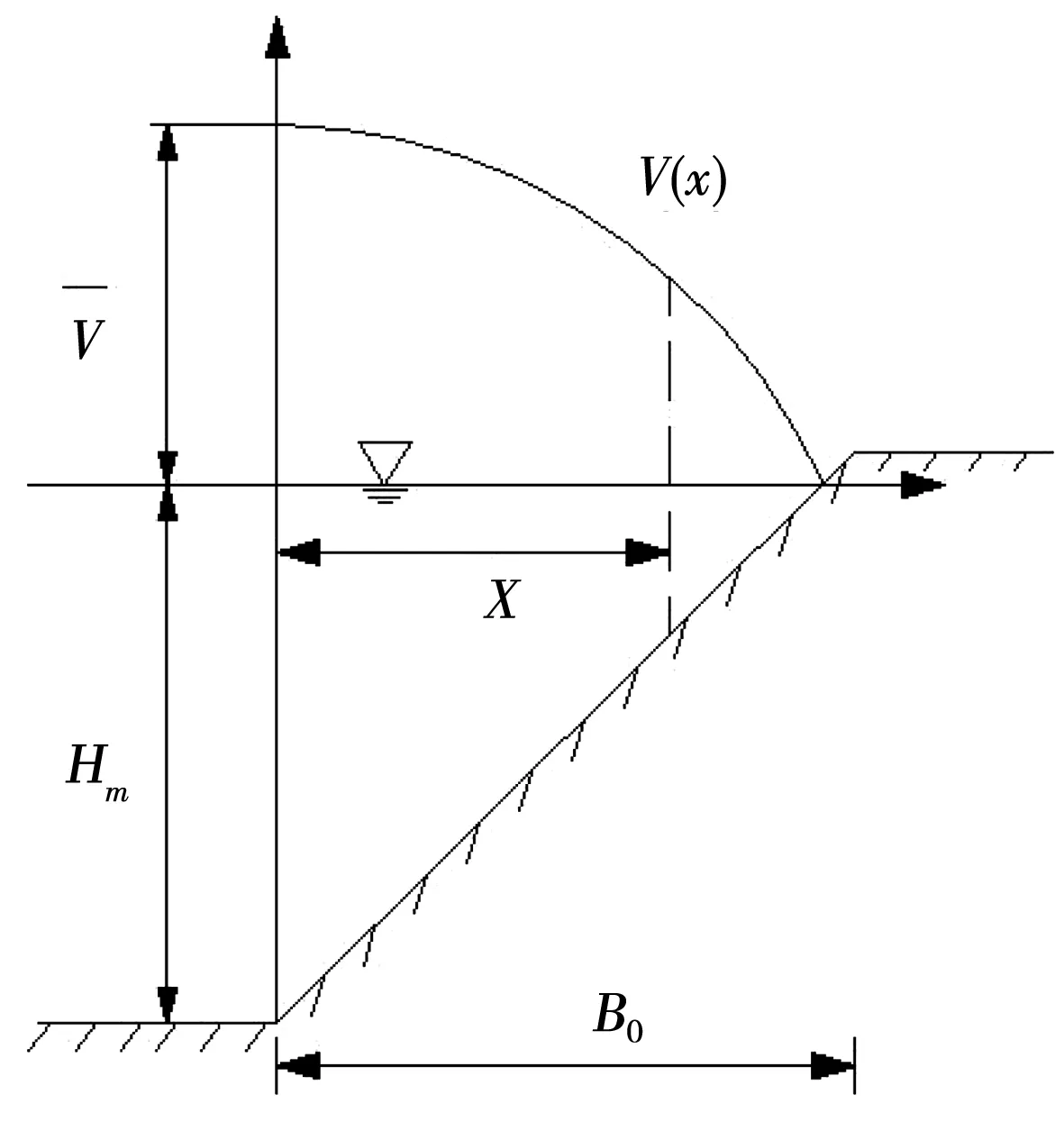
图1 横向流速分布为二次抛物线型
则流速分布曲线为:
(2)
假设水面与边壁的交点处流速为0,则x=B0,v(B0)=0代入(1)式得:
(3)
则横向流速面积公式为:
(4)

(5)
因此岸边流速系数:
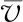
1.2 横向流速分布为梯形分布
假设梯形渠道边壁横向流速分布为梯形,见图2。

图2 横向流速分布为梯形
则边壁处流量为:
(6)

(7)
近边壁处面积A为:
(8)
故近边壁处流速为:
(9)
1.3 横向流速分布为三角形分布
假设梯形渠道边壁横向流速分布为三角形分布,见图3所示。

图3 横向流速分布为三角形
则有:
(10)
(11)
则第一条垂线至边壁的流量为:
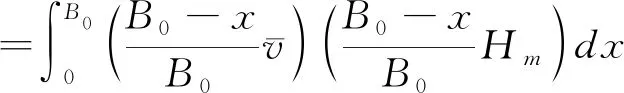
(12)
故近边壁处流速为:
(13)
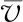
当岸边横向流速分布趋于二次函数分布曲线时,推求岸边流速系数为0.833,此时的岸边流速系数与坡度无关,说明缓坡的岸边流速系数也有可能大于0.8,并非只有陡坡的岸边流速系数才能大于0.8;岸边流速系数应该与影响流速分布的因素有关,如壁面粗糙度。岸边横向流速分布为梯形时,这是由于距岸边最近的第一垂线不一定设置在坡脚位置,因此将横向流速分布假设为梯形,此时的岸边流速系数与第一条垂线位置有关,当第一条垂线离岸边越近,岸边流速系数越小。当岸边横向流速分布为三角形时,这是岸边横向流速分布最不利情况,推求岸边流速系数值为0.67,与规范中给出的岸边为斜坡时的岸边流速系数最小值相同;廖喜庭[2]对岸边系数的影响因素进行了分析,发现第一条测速垂线离岸边越近,岸边流速系数越大;还提出水深变化也会影响岸边流速系数,水深越深,岸边流速系数越小。然而,陈存发[3]认为水深越大,近岸边部分面积越大,岸边流速系数越大;并提出糙率越大的渠道应选用较小的岸边流速系数。
综上所述,前人对水深与岸边流速系数关系的研究结果并不一致,有待考究,且对梯形渠道有边壁附着物情况的岸边流速系数的研究仍较少,故本文对渠道边壁加糙后的岸边流速系数进行研究。
2 试验概况
试验在长L为4 m,底宽B为0.35 m,高H为0.133 m,边坡系数m为1.5,以及底坡i为0.000 5的梯形渠道中进行。在梯形渠道上游3.4 m段铺设塑料板,以便粘贴糙体。渠道分为20个断面,相邻两个断面间距为20 cm。试验段为cs7至cs16,长1.8 m,共10个断面。将5 mm×5 mm×6 mm的有机玻璃块作为糙体,粘于渠道边壁上,采用梅花型加糙方式,横距与纵距均为30 mm。流量为5~8 L/s,尾门开度为15°、19°和23°。
3 试验过程
上游进水口布置三角堰,测量进口流量。通过人字型尾门调节渠道水位。将水位测针布置在试验段每个过水断面中轴线处测量渠道水深,即距两侧坡脚处17.5 cm,水位测针精度为±0.1 mm。流速使用电磁流速仪进行量测。流速测量时,严格按照水文测量规范,每个测量断面分别布置左中右垂线和左右边壁垂线,左右测线分别布置在距左右坡脚3 cm处,中间测线布置在断面中点处,左右边壁垂线布置在边坡上;也就是距左岸0.17、0.2、0.375、0.52和0.58 m处的5条测速垂线。据不同的水深情况,合理布置垂线测点数。
4 岸边流速系推求
限于篇幅,选取流量为8 L/s、尾门开度为15°的横向流速分布进行分析。见图4。
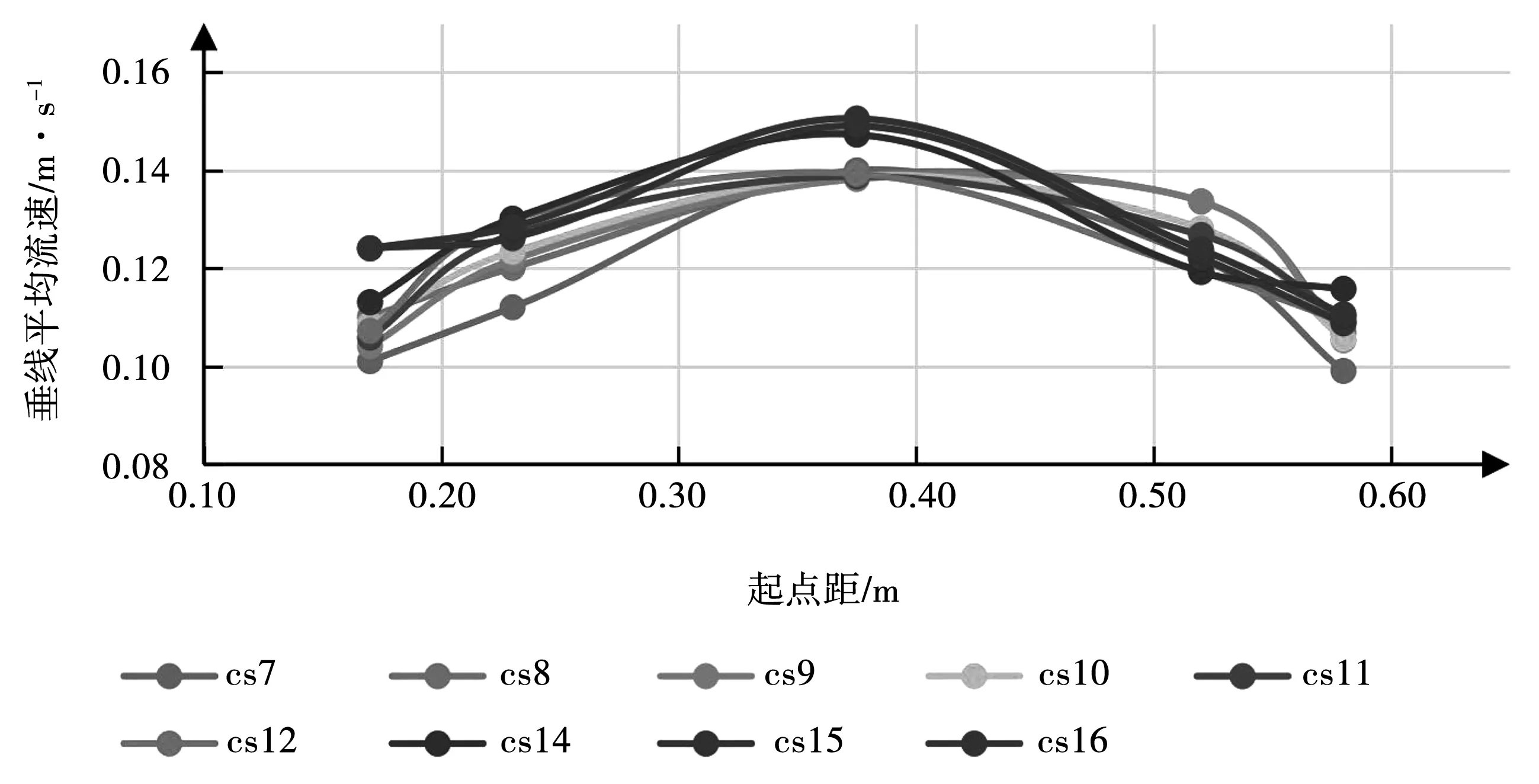
图4 横向流速分布图
由横向流速分布图(图4)可看到,渠道边壁加糙后,每个横向断面流速分布接近二次函数,越靠近两侧边壁,其垂线平均流速越小。这是因为受到边壁糙体影响,中垂线流速较大,符合主流流速最大的规律。
根据横向断面流速分布图,拟合横向流速分布公式V(x)。由于过水断面流量等于断面面积与断面平均流速的乘积,故可列积分公式求过水断面流量:
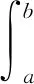
(14)
式中:Q为过水断面流量,m3/s;a,b分别为水面与左右边坡交点到左岸的距离,m;x为与左岸的距离,m;V(x)为拟合横向流速公式。
左中右测速垂线间面积按矩形面积公式计算,边壁面积按三角形计算:
αA1V0.58
(15)
式中:α为岸边流速系数;A1为左右垂线与水边之间的梯形面积,m2;A2为左右垂线与中垂线间的矩形面积,m2;Vi为与左岸距离为i的垂线平均流速,m/s。
由Q1=Q2求出岸边流速系数α,计算结果见表2。

表2 岸边流速系数结果
由表2可看到,流量越大,水深越深,导致边壁的水面越宽,对应部分的面积越大;加上水深变大后,边壁糙体的阻水作用越强,流速较小,因此岸边流速系数越大,说明不同水位的渠道选用的岸边流速系数是有差别的。
当尾门开度变大时,水深变浅,且尾门的顶托力减弱,因此流速会变大;加上水面宽度较小,导致岸边流速系数较小。据相关文献可知,边坡系数同为1.5的未加糙梯形渠道岸边流速研究结果为0.83~0.87[3],与本试验加糙后的岸边流速系数比较发现,加糙后的岸边流速系数偏小,说明渠道糙率越大,岸边流速系数越小。因此当渠道边坡有附着物时,应根据实际的渠道糙率选用不同的岸边流速系数值。
5 结 语
根据上文分析结果,笔者认为在利用流速仪测流量时,不能仅参考规范中的取值范围,而应根据实际情况,考虑水深、水生生物的生长造成渠道糙率变化等因素对岸边流速系数的影响,再选用合适的岸边流速系数。

