基于深度学习决策融合的非侵入式负荷分类的研究
滕红丽,贾树恒,王灏,王雅倩,周东国,胡文山,袁超
(1.河南农业大学理学院,河南 郑州 450002;2.武汉大学电气与自动化学院,湖北 武汉 430072)
负荷监测作为高级测量体系(Advanced Metering Infrastructure,AMI)最重要的组成部分[1],是实现智能电网的关键技术之一。其中,非侵入式负荷监测(Non-intrusive load monitoring,NILM)[2]以软算法代替硬测量,具有经济适用、易推广等优点,逐步取代了侵入式测量,成为新的研究热点。NILM仅利用电力入口处的单一测量装置即可有效获取负荷电气信息,结合软件算法有针对性地分析、管理用户用电行为,从而实现需求侧精细化管理和智能用电双向信息流交互[3-4]。
目前,负荷识别及分类方法以模式识别[5]为主,主要通过学习负荷印记(Load Signatures,LS)实现负荷分类,例如支持向量机、K最邻近算法、神经网络等,国内外相关研究众多。FIGUEIREDO等[6]提取负荷电流和电压的峰值、均方根以及功率因子等特征作为负荷印记标记电气设备。LIN等[7]结合Fuzzy、C-Means和模糊分类方法,能够较好地处理负荷特征相似问题,其性能优于BP(Back Propagation)神经网络;WANG等[8]提取V-I轨迹曲线,通过支持向量机多分类算法实现负荷辨识;DU等[9-10]深入研究了负荷V-I轨迹特征,并通过多种设备证明V-I轨迹图像作为负荷分类特征的优势以及卷积神经网络(Convolutional Neural Networks,CNN)对图像的分类效果;HONG等[11]利用傅里叶变换(Fast Fourier Transform,FFT)获得电流、电压、有功功率、无功功率等4种负荷印记,构成7种组合特征,研究发现4种负荷印记组合时能获得最高精度。HE等[12]采用双层特征提取框架融合不同负荷特征的优势,具备较强的可扩展性。KELLY[13]采用3种深度学习神经网络架构,在负荷分解方面取得良好的分类效果。MAUCH等[14]采用长短时记忆序列网络(Long Short Term Memory Network,LSTM)模型通过使用电器运行时的时间序列特性进行负荷分解,对负荷功率特征具有较好的辨识效果。但这些研究也存在一些不足,V-I轨迹图特征比其他高频特征具有更高的辨识准确率,但不能有效区分V-I轨迹图相似但功率差异较大的设备;功率特征也存在相同情况,单独使用功率特征,也无法较好的区分功率特征相似但V-I轨迹图差异较大的设备。
相对于单一特征,组合特征能够更全面反映不同负荷电气特点,从而获得更高的辨识精度。多层次的综合辨识模型能够更好地提高辨识效果和复杂场景适用性,其中集成学习表现优秀。本研究提出一种基于深度学习决策融合的非侵入式负荷分类方法。首先从原始负荷电气信息中提取负荷稳态特征(有功功率P、无功功率Q和V-I轨迹图)以及利用傅里叶变换得到电流谐波特征H。其次,将P、Q、H3种特征组合为PQH特征,通过归一化处理后作为LSTM神经网络的输入,进行负荷第一层辨识。将V-I轨迹图特征进行图像二值化处理,作为CNN网络的输入,进行负荷第二层辨识。最后采用决策融合方法对两个辨识模型进行融合,实现负荷分类,并使用公共数据集对算法的分类性能进行测试。
1 多特征负荷印记
负荷特征的选取是决定模型性能优劣的因素之一,应满足以下基本要求:1)尽可能反映设备的电气特性;2)能够和其他设备进行区分;3)降低不同特征之间的相关性,减少冗余,以提高模型效率。目前常用负荷印记有有功功率P、无功功率Q、电流波形、电流谐波、谐波畸变率、V-I轨迹图等。
1.1 PQH特征
1.1.1 功率P、Q特征 设备的有功功率P和无功功率Q属于低频特征,利用快速傅里叶变换得到。设采样点数为N的时域电压和电流信号分别为v(n)和i(n),n=0,…,N-1,则有
(1)
(2)
式中:V0和I0分别为基波电压和电流有效值,Vk和Ik分别为第k次谐波电压和电流有效值,θk和φk分别为第k次电压和电流谐波的相位角,f0为设备工作频率。
将(1)、(2)式进行FFT变换,得到功率P、Q表达式。
(3)
(4)
1.1.2 电流谐波H特征 高频次的特征信息中,电流谐波反映了用电设备在投入过程中电感、电容等高频特性,例如电流谐波畸变能够反映基波和高次谐波的比例成分,负荷特征表达中,常将其作为一个负荷印记。设利用FFT方法得到k阶频域电流信号为
I(k)=A(k)+jB(k)
(5)
式中:k=0,1,…,N-1,j为虚数单位,A(k)和B(k)分别为第k阶频域信号的实部和虚部。基波和各电流谐波分量有效值如式(6),(7)。
(6)
(7)
(8)
式中:||为取模。
1.1.3 特征归一化 若直接将特征P、Q、H用于训练神经网络,功率和谐波特征的数值数量级差异较大,会降低较小值(电流谐波)的重要性,因此需要进行归一化处理。常用归一化方法有min-max归一化和z-score归一化。min-max归一化对数据的处理是线性的,若数据中含有离群点时,会降低不同类型数据差异,产生不利影响。z-score归一化法能够克服离群点的影响,更适用于功率和谐波特征数值差异较大的情况,因此采用z-score归一化法。
原始数据序列x1,x2,…,xn,将其转换为均值为0,方差为1的标准数据,得到yi,i=1,2,…,n。
(9)

(10)
(11)
将P、Q、H特征数据作为3个原始数据序列,根据式(9)—(11)对每一个序列进行归一化处理。
1.2 V-I轨迹图特征
V-I轨迹图反映了一个工作周期内电压和电流的关系。BAETS等[10]验证了V-I轨迹图作为负荷分类特征的有效性和优势性。传统的V-I轨迹图特征将其形状数据作为辨识模型的输入,方法复杂且易造成特征缺失。DU等[9]将V-I轨迹图映射到基于二进制值的单元格网络,结果表明二值化的V-I轨迹图是一种容易提取且十分有效的特征。
对一个工作周期的电压、电流采样,得到采样点v(n)和i(n)。设V-I轨迹二值图的像素为w×w,根据式(12)将v(n)和i(n)线性变换为[0,w]区间的整数。
(12)
式中:Vn和In为变换后的电压和电流值,vn和in为v(n)和i(n)中第n个采样点的值,vmax和imax为v(n)和i(n)的最大值,vmin和imin为v(n)和i(n)的最小值,⎣」表示向下取整。
像素为w×w的二值图像,以像素为单位将其视为一个w×w的矩阵X,矩阵元素的值取决于是否被V-I轨迹覆盖:若被覆盖则该矩阵元素为1,否则为0。矩阵X计算方法如式(13),(14)。
(13)
(14)
式中:n=0,1,…,N-1;i,j∈[0,w-1]。
2 基于深度学习的决策融合模型
归一化后的P、Q、H特征都是时间序列,可以进行组合。LSTM网络作为经典的改进RNN神经网络之一,主要用于序列化信息的识别。LSTM网络增加了记忆模块,能很好地避免梯度消失现象的发生。研究采用LSTM模型对PQH组合特征进行训练和学习。V-I轨迹图是二值化图像,考虑到卷积神经网络在图像分类上表现优秀,同时兼顾负荷分类的性能、模型复杂度和训练时间,研究采用基于LeNet-5的CNN神经网络模型,使用V-I轨迹二值图做负荷印记进行负荷分类。假设2个网络的辨识结果分别为Y1、Y2,利用决策融合方法将Y1和Y2融合,得到最终分类结果Y。研究使用4种指标和混淆矩阵对LSTM、CNN和决策融合模型的分类结果进行评价。决策融合模型负荷辨识框架如图1所示。

图1 非侵入式负荷辨识框架Fig.1 Non-intrusive load identification framework
2.1 基于PQH特征的LSTM模型
LSTM和CNN网络模型中,负荷印记采用one-hot编码方式生成;输入层的神经元数量和输入特征向量长度相同;输出层神经元个数为设备种类数。LSTM网络主要基于时间序列,具有历史记忆特性,适合于能抽取时间序列特征参数的负荷辨识。本研究中LSTM网络的层数和时间序列长度相同,设置为10;隐含层神经元个数为48,权重矩阵内所有元素的值在区间(-1,1)内初始化。Softmax函数作为输出层激活函数,使用对数似然函数中的交叉熵函数作为损失函数,这样不仅能提高模型训练速度,还有助于解决梯度消失问题。
2.2 基于V-I轨迹特征的CNN模型
CNN模型以LeNet-5网络为基础,在图像分类领域具有较好的性能和较大的应用潜能。为保证降维效果和特征提取精度,降低结构复杂性,模型结构设置如下:第一层为输入层,输入维数和矩阵维数相同;第二层为第一卷积层,使用12个卷积核,每个卷积核大小为3×3;第三层为第一池化层,池化大小为2×2;第四层为第二卷积层,使用24个卷积核,每个卷积核大小为3×3;第五层为第二池化层,池化大小为2×2;第六层为全连接层,设置128个神经元,在保证训练集拟合效果的同时避免过拟合;第七层为输出层,神经元数量等于期望输出的负荷印记向量长度。
为帮助模型分辨特征差异较小的类别,同时使训练能快速收敛,使用Relu函数作为CNN卷积层和全连接层的激活函数;多分类问题中常用的Softmax函数作为输出层激活函数。损失函数使用交叉熵函数。
2.3 决策融合方法
集成学习是将多个不同的基础分类器组合成一个集成模型的方法,集成学习有助于降低分类模型的偏差和方差,提高模型性能,降低过拟合风险,具有比单一学习器更显著优越的泛化性能。决策融合是集成学习中多模型组合方法。常见的集成策略有平均法、投票法和学习法。平均法主要针对回归任务;投票法主要针对分类任务;学习法是一种更为强大的集成策略,需要较多的训练数据。结合算法的分类目标和训练数据体积,本研究采用投票法作为LSTM和CNN模型融合方法。

投票法中,绝对多数投票法和相对多数投票法适用于3个或3个以上分类模型的情况,而基于合适权重的加权投票法同样可以获得较好的决策结果,本研究采用加权投票法实现模型融合。考虑到不同分类模型对不同负荷设备的分类效果会出现一定差异,引入决策权重矩阵对加权投票法进行改进。改进的加权投票法通过对LSTM模型和CNN模型输出向量的每一个元素设置权重,这样可以克服加权投票法不能反映分类模型的辨识偏好等问题。模型融合原理如图2所示。

图2 决策融合原理图Fig.2 Schematic diagram of decision fusion
(15)
H(x)=cargmaxjY
(16)
式中:Y为集成后的输出向量,Wi为hi的权重向量,符号“⊙”表示按元素乘,argmax()表示获取向量最大元素的下标。H(x)为运算后得到融合模型分类结果。
所有的权重向量Wi可组成权重矩阵W。
(17)
式中:wi,j为hi的第j个类别输出权重,且有
(18)
2.4 评价指标
在分类任务[15]中,用于评价分类模型好坏的指标有混淆矩阵(Confuse Matrix)、准确率(Accuracy rate,A)、精确率(Precision ratio,P)、召回率(Recall rate,R)、F1值等。混淆矩阵也称误差矩阵,是表示精度评价的一种标准格式,用行、列数相同的矩阵形式来表示,各矩阵元素通过将每个实测像元的位置、分类与分类图像中的相应位置和分类相比较计算。其他4个指标计算方法如表1所示。

表1 评价指标说明Table 1 Description of evaluation indexes
(1)混淆矩阵反映了分类结果的混淆程度,最大的优点是具有直观性,可以清楚观察模型的分类效果。用行代表样本的实际类别,列代表模型的分类结果,则第i行第j列的数值表示模型将实际类别i分类为类别j的样本数量;对角线元素表示分类正确的样本数量。
(2)因每类设备的实例数量远小于总设备实例数量之和,评价过程中正、负样本数量差异过大,会造成指标结果虚高等问题,因此单一的准确率指标无法全面反映模型优劣。本研究使用混淆矩阵、准确率、精确率、召回率和F1值多重指标对模型进行更加综合、全面的评价。
3 试验结果与分析
为验证模型的有效性,使用插件级设备标识数据集(Plug-Level Appliance Identification Dataset,PLAID)进行测试。该数据集包含56户家庭,11类不同电气设备(空调,电风扇,电吹风,电暖器,电冰箱,荧光灯,白炽灯,微波炉,笔记本电脑,吸尘器,洗衣机)的采样数据。每类设备包含数十个不同品牌和型号的电气设备,共1 074条原始样本,如表2所示。每条样本数据包含30 kHz采样频率下时长2~5 s的设备电压、电流波形,包括设备启动时的瞬态数据和设备运行一段时间后的稳态数据,每个工作周期的采样点数N=500。

表2 PLAID数据集设备种类统计表Table 2 Equipment type statistics of PLAID data set
由于PLAID数据集中不同类别设备样本数量差异较大,荧光灯样本最多,有175条,洗衣机样本最少,只有26条。为了避免数据不平衡降低模型辨识性能,预先采用合成少数类过采样技术(Synthetic Minority Oversampling Technique,SMOTE)对原数据集进行扩充,使每类设备样本数均达到样本最多设备类别的样本数175,扩充后总样本数为1 925条。
因PLAID数据集作者已做去噪处理,研究直接从每个原始样本中截取最后10 000个采样点,即20个工作周期,约0.33 s,并按位计算中位数将其压缩为一个工作周期的稳态数据,数据长度N=500。
3.1 特征提取
使用扩充后的数据集提取有功功率P、无功功率Q、电流谐波H和V-I轨迹图。因设备品牌、型号和工作档位(例如:空调、电吹风等)不同,提取的部分设备P-Q二维特征存在重叠现象,这会在一定程度上影响辨识效果。大部分电风扇样本和其他设备也出现了不同程度的混叠,因此电风扇的辨识准确度可能较低。
图3给出提取的11类设备的前16次电流谐波。由图3可知,各设备的偶次电流谐波均可忽略不计,奇次电流谐波随谐波次数增加呈下降趋势,且大部分设备在第3次谐波时幅值已经较小,说明高次谐波对负荷分类贡献相对较小。本研究使用第1、3、5次电流谐波作为电流谐波特征,加上P、Q特征,LSTM模型的输入层神经元数目为5(P、Q,电流1、3、5次谐波),从而降低模型复杂度,便于工程化应用。

图3 不同种类设备的电流谐波直方图Fig.3 Current harmonic histograms of different kinds of equipment
图4给出提取的11类设备V-I轨迹图。图5给出二值化后的V-I轨迹二值图。分析可知,这些设备的V-I轨迹图存在一定差异,但少部分样本(例如空调、白炽灯、电风扇和电冰箱)的V-I轨迹图有一定程度的相似性,可能影响辨识效果。

图4 不同种类设备的V-I轨迹图Fig.4 V-I trajectory original graphs of different kinds of equipment

图5 不同种类设备的V-I轨迹二值图Fig.5 V-I trajectory binary graphs of different kinds of equipment
3.2 单一模型和决策融合模型对比
3.2.1 LSTM模型 将提取后的PQH特征集按4∶1分为训练集(1 540条样本)和测试集(385条样本),输出神经元个数为设备种类数11,训练轮数为500,使用小批量梯度下降法,设置每次迭代使用20个样本对参数进行更新。使用测试集对训练好的最佳LSTM模型进行测试,得到混淆矩阵和A、P、R、F1指标如图6-a和表3所示。

由图6-a和表3可知,每类设备的准确率均高于95%,由于正负样本比例(1∶10)差异较大,不同设备的准确率差异不大。精确率评价中,电冰箱和白炽灯评价结果最差。从混淆矩阵可以看出,这是由于电风扇辨识结果造成的电冰箱和白炽灯假正例(FP)较多。召回率评价中,LSTM模型对电风扇的辨识性能较差,由特征分析可以看出,这是由于电风扇的PQH分布与其他设备重叠较多。F1评价结果对精确率和召回率进行综合。
3.2.2 CNN模型 将V-I轨迹二值图特征集按4∶1分为训练集(1 540条样本)和测试集(385条样本),输出神经元个数为设备种类数11,迭代次数为500,使用小批量梯度下降法,设置每次迭代使用20个样本对参数进行更新,每轮训练迭代77次。使用测试集对最佳CNN模型进行测试,得到混淆矩阵和A、P、R、F1指标如图6-b和表3所示。
由表3可知,每类设备的准确率均高于95%;其他3个指标在空调、电风扇、电冰箱、白炽灯和洗衣机5类设备上的评价结果不够理想。从V-I轨迹二值图和混淆矩阵可以看出,这是由于这5类设备的V-I轨迹图像形状近似,给辨识带来难度。LSTM和CNN分类结果进行对比发现,基于不同特征的2个模型对不同种类设备的辨识上能够互补,可以进行模型融合。
3.2.3 基于多特征的决策融合模型 使用的评价指标中,准确率A和精确率P的计算涉及正负样本,每类设备的正、负样本数量存在较大差异时,这2个指标不适合作为反映融合模型对各设备适配度的决策准则。本研究选择召回率R构建决策权重:记LSTM和CNN对第j类设备的测试召回率分别为p1,j和p2,j,则决策权重矩阵元素计算公式如式(19)。
(19)
式中:T=2为融合模型数量。根据表3的召回率,计算得到决策权重矩阵如式(20)。

表3 LSTM、CNN和融合模型测试集的A、P、R和F1指标Table 3 A,P,R and F1 indicators of the test set of LSTM,CNN and Fusion Model %
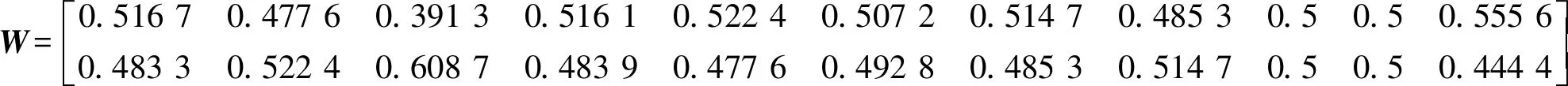
(20)

1.空调;2.电风扇;3.电吹风;4.电暖器;5.电冰箱;6.荧光灯;7.白炽灯;8.微波炉;9.笔记本电脑;10.吸尘器;11.洗衣机。1.Air conditioner;2.Electric fan;3.Electric hair dryer;4.Electric heater;5.Electric refrigerator;6.Fluorescent lamp;7.Incandescent lamp;8.Microwave oven;9.Laptop;10.Vacuum cleaner;11.Washing machine.图6 3种模型的混淆矩阵 Fig.6 Confusion matrixes of three models
决策融合模型的混淆矩阵和A、P、R、F1指标如表3和图6-c所示。由表3可知,在单类设备辨识中,从准确率A、精确率P、召回率R和F1单一评价指标分析,决策融合后大部分设备的评价结果均优于或等于LSTM和CNN的评价结果,其余均介于二者之间。
从表3可知,决策融合模型的A、P、R、F1 4种评价指标均高于LSTM模型和CNN模型的单独辨识结果。总体来说,决策融合方法能够有效融合LSTM和CNN两种模型,融合辨识模型效果优于单一模型辨识效果。
3.3 不同辨识方法对比
3.3.1 特征组合对比 单一谐波特征H、单一功率特征P、组合特征PQH使用LSTM模型的辨识结果如表4所示。从表4可以看出,PQH组合特征能够在一定程度上提高LSTM模型辨识性能。由特征分析可知,功率相近的负荷分类中增加谐波特征,谐波特征相似的负荷分类中增加功率特征,均可从另一维度帮助区分,从而提升辨识结果准确性。

表4 LSTM模型不同特征评价指标Table 4 Evaluation indexes of LSTM model based on different features %
3.3.2 不同文献算法对比 文献[16]将BP网络提取的功率特征和LeNet-5网络提取的V-I轨迹特征进行组合,再利用BP神经网络实现负荷分类。文献[17]使用稳态电流的1,3,5次谐波幅值和相角组成负荷印记,使用多层感知机(Multilayer Perceptron,MLP)算法进行负荷分类。文献[18]使用经椭圆傅里叶描述子简化的V-I轨迹作负荷印记,使用随机森林算法实现负荷分类。文献[19]使用自动选择设备特征的递归特征消除(Recursive Feature Elimination,RFE)算法,负荷分类用随机森林算法。文献[20] 使用稳态与暂态特征相结合的混合特征,使用基于主成分分析(Principal components analysis,PCA) 的辨识分类算法(Identification and Localization based on PCA,ILPCA)进行负荷分类。这些研究均在PLAID数据集上进行,各负荷辨识算法的准确率如表5所示。从表5可以看出,除电吹风和白炽灯的准确率本研究略低于文献[16]、[19]、[20]外,其余设备准确率均高于或等于其他文献算法;本研究所有设备的平均准确率高于其他几种算法。

表5 本研究与其他文献算法准确率的对比Table 5 Comparison of accuracy rate with other literature algorithms %
4 结论
本研究提出一种基于多负荷特征和决策融合方法的非侵入式负荷分类辨识方法。该方法使用有功功率P、无功功率Q、电流谐波H、V-I轨迹图等负荷特征,以期更大范围反映设备特性,更深维度区分不同种类设备。本研究利用z-score归一化方法构建组合PQH特征,并对V-I轨迹图二值化。选择LSTM模型和CNN模型进行辨识分类,使用加权决策对2个模型进行融合,进一步提高负荷辨识效果,克服了单一特征或单一模型无法较好辨识特征相似负荷的弊端。
研究结果表明,在准确率A、精确率P、召回率R、F1值4种评价指标上,LSTM模型的平均结果分别为98.57%、94.04%、92.47%和92.21%;CNN模型的平均结果分别为98.45%、92.11%、91.94%和91.94%;改进后的决策融合模型的结果分别为99.32%、96.36%、96.36%和96.34%。通过分析发现,在4种指标的性能表现上,决策融合模型的表现均优于单一模型,说明本研究提出的基于多特征组合的决策融合模型能更有效地实现负荷分类,从而为非侵入式负荷辨识提供一种有效可行的新方法。

