基于Archimedean Copula-EGARCH模型对我国股票市场的相关性研究

王善培， 李兴东

(兰州交通大学 数理学院，甘肃 兰州 730070)

在经济全球化进程的影响下，金融市场各板块之间的联动关系也日渐加强，目前学者更注重多个金融市场间的联动，试图找到股市波动的传染源与传导路径。Copula函数模型可以结合ARIMA或GARCH类模型建立多变量Copula-ARIMA或Copula-GARCH模型来刻画金融数据，分析金融市场间的相关程度和相关关系，同时能够及时捕捉到金融市场的各种特点。目前研究更多的是Copula-GARCH模型，其对金融时间序列时变波动、波动聚类、尖峰厚尾、非对称性这些特点的描述有一定优势。韦艳华等[1-3]对于Copula-GARCH模型的构建和应用已有许多研究；学者们还从Copula函数构造方向出发，构造新的二元Copula函数来构建更多新模型[4]，或不仅仅局限于两种序列之间构造模型分析关系[5-6]；对金融关系往往认为是对称的，但实际并不一定是对称的，可能存在杠杆效应，对边缘分布的拟合往往直接采用GARCH模型[7]，这是不够准确的。因此本文利用指数GARCH(EGARCH)模型结合Archimedean Copula函数对4种板块的收益序列进行拟合分析，决策出最优模型，适应股市变化，及早预防，规避风险，获取最大利益。

1 模型的构建

EGARCH模型能够反映波动的非对称性，具有较强地刻画金融波动的能力，结合Archimedean Copula理论和EGARCH模型可以有效分析股市之间的非线性关系。

1.1 边缘分布的确立

GARCH模型可以刻画时间序列的波动性，EGARCH模型能够反映其波动的非对称性，t分布可以描述其时变性，所以用EGARCH-t模型刻画各股市板块收益率数据，其中EGARCH-t模型如下：

(1)

式中yt是收益序列，μt是收益的均值，ht表示εt的条件方差，ω、α、β、θ分别是模型的参数，g(·)满足Et-1[g(ξt)]=0，t(ν)代表自由度为ν的标准t分布。

1.2 二元Archimedean Copula函数的选择

(1)Gumbel-Copula的分布函数和密度函数分别为

(2)

(3)

其中参数α∈(0，1)。

(2)Clayton-Copula的分布函数和密度函数分别为

(4)

(5)

其中参数θ∈(0，+∞)。

(3)Frank-Copula的分布函数和密度函数分别为

(6)

(7)

其中参数λ≠0。

2 实证分析

2.1 数据样本选取及分析

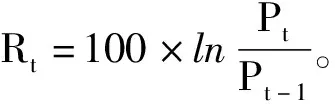
对4组收益率序列进行建模之前，需对它们各自建立边缘分布模型。首先判断它们能否用EGARCH模型来建立条件边缘分布，需对4组序列进行基本统计分析。如表1所示，4组序列的峰度均大于3，偏度均小于0，所以左偏和尖峰的特点表现明显。同时4组序列的JB统计量分别是2 263.985 0、8 838.957 1、406.567 7、818.679 5，且P值均小于0.05，所以正态假设被拒绝。此时可以用GARCH模型来建立条件边缘分布。

表1 4组序列的描述性统计结果

2.2 边缘分布模型的确立

检验序列是否平稳可以用单位根检验来判断，上证、深证、创业板和中小板这4组序列的单位根统计量分别为-30.126 82、-29.672 50、-29.744 72、-28.977 75，其对应的P值均为0.000 0，则这4组序列均不是单位根过程，均是平稳序列。此时便可构造条件均值模型yt=μt+εt，并且进行ARCH效应检验，发现这4组数据的F统计量分别为72.205 82、51.094 00、83.301 64和50.211 25，且P值均为0.000 0，说明存在异方差性，可以构造GARCH模型。由于序列存在非对称性即杠杆性，所以选择构造EGARCH模型，EGARCH(1，1)模型的最小信息化准则(Akaike information criterion,AIC)值最小，并且由图1可知序列具有时变波动和波动聚类的特点，所以选用EGARCH(1，1)-t模型来拟合条件边缘分布，表2是得到的边缘分布的参数估计结果。

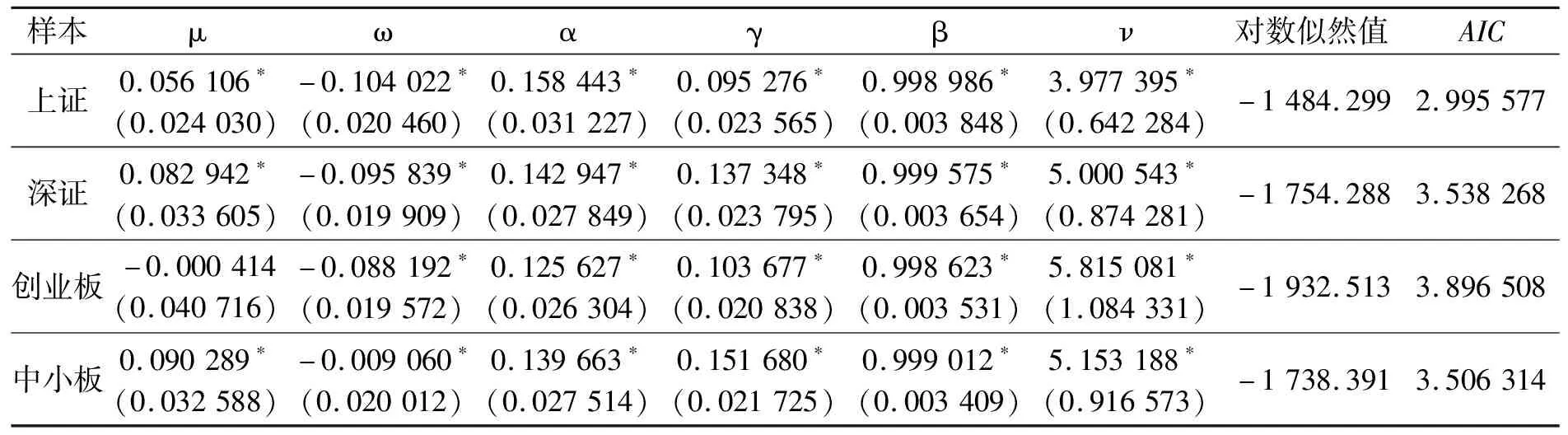
表2 EGARCH(1，1)-t模型的参数估计

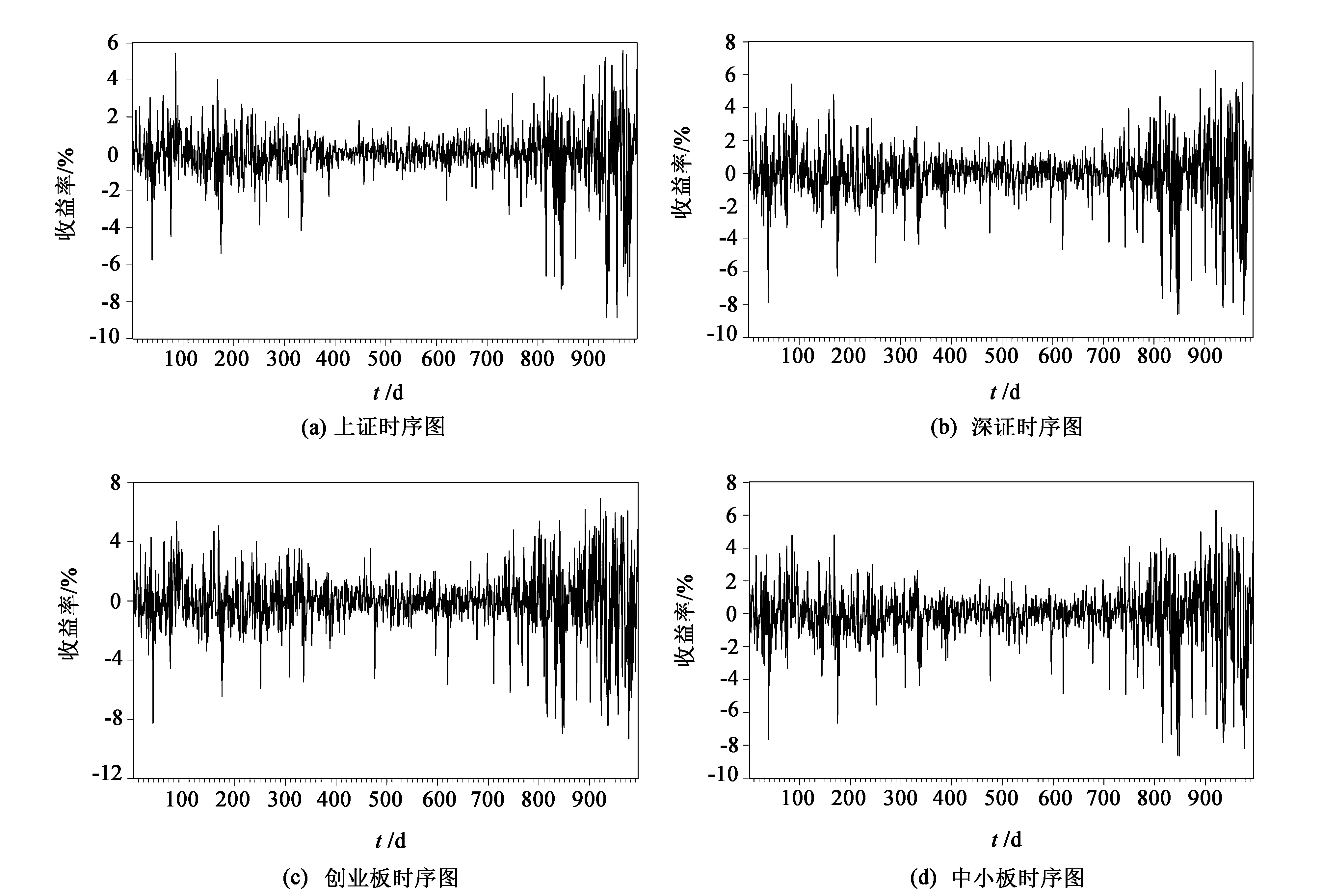
图1 日收益率序列时序图

EGARCH模型的条件方差方程也可表示为

另外，根据估计得到的EGARCH(1，1)-t模型，可以得到上证、深证、创业板和中小板收益序列的残差序列{ξ1t}、{ξ2t}、{ξ3t}和{ξ4t}，图2给出了这4组残差序列的分布与对应t分布的分位数对比图(Q-Q图)，4个分位图都直观地表明了EGARCH(1，1)-t模型能够很好地拟合各序列的条件边缘分布。

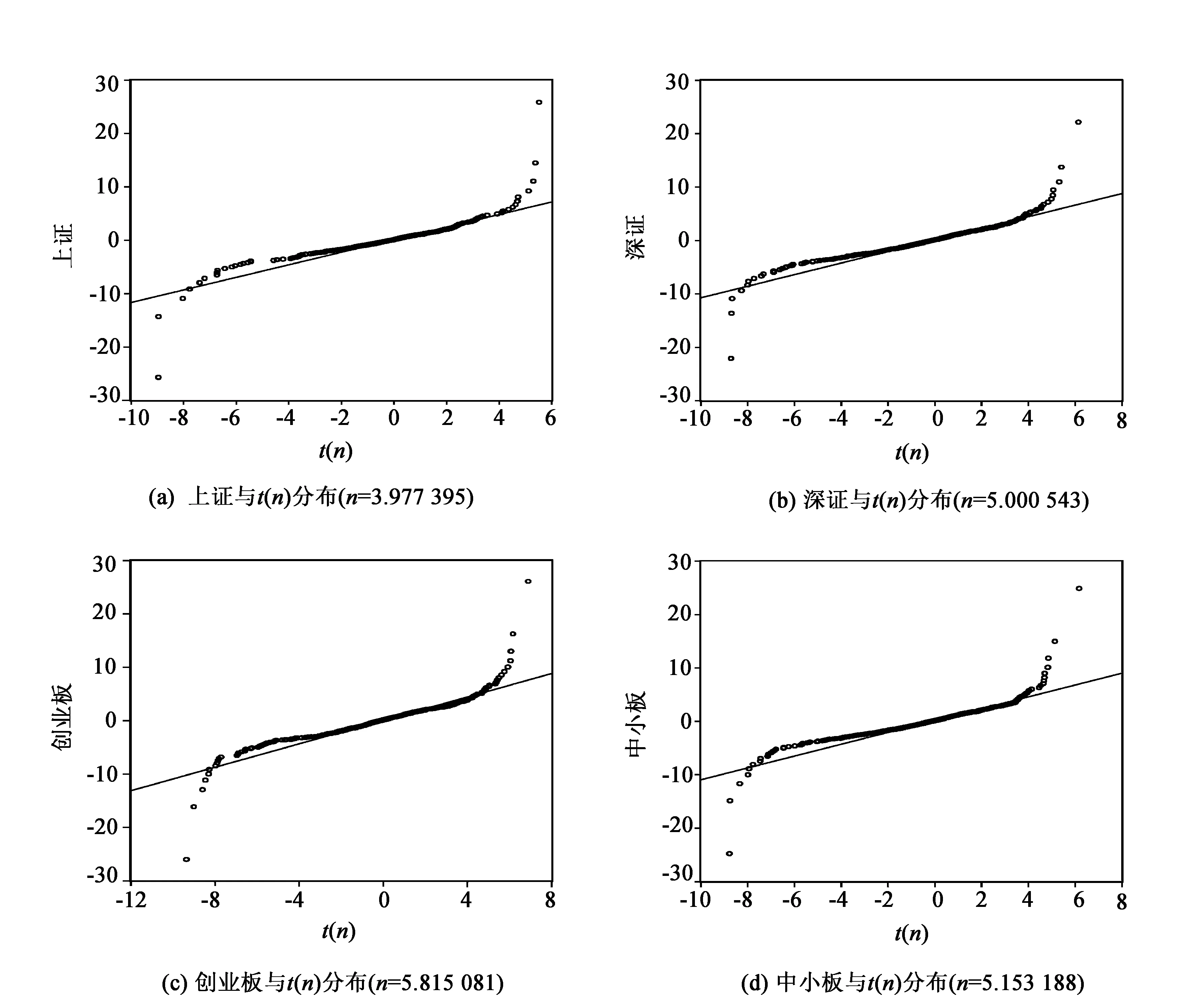
图2 条件边缘分布模型的拟合度Q-Q图

2.3 Archimedean Copula的选择

根据条件估计得到的EGARCH(1，1)-t模型可以确定上证、深证、创业板和中小板收益序列的条件边缘分布，根据得到的条件边缘分布，对原序列进行概率积分变换后可以得到4个新序列，分别用Gumbel Copula、Clayton Copula和Frank Copula函数来描述新序列间的相关关系，得到表3所示的参数估计结果。结果显示了这4种组合分别用3种Copula函数计算出Kendall秩相关系数和平方欧式距离，可以看出Kendall秩相关系数均大于0，说明这4种组合均呈正相关。再观察平方欧式距离发现每种组合里Gumbel Copula函数的平方欧式距离最小，说明Gumbel Copula函数对数据的拟合效果最好。根据Gumbel Copula函数绘制出密度函数图，如图3中(a)、(b)所示可知创业板和深证的组合具有更厚的尾部，说明深证指数对于创业板指数的影响强于上证指数对于创业板指数的影响。由图3中(c)、(d)可知中小板受深证指数的影响也更强。

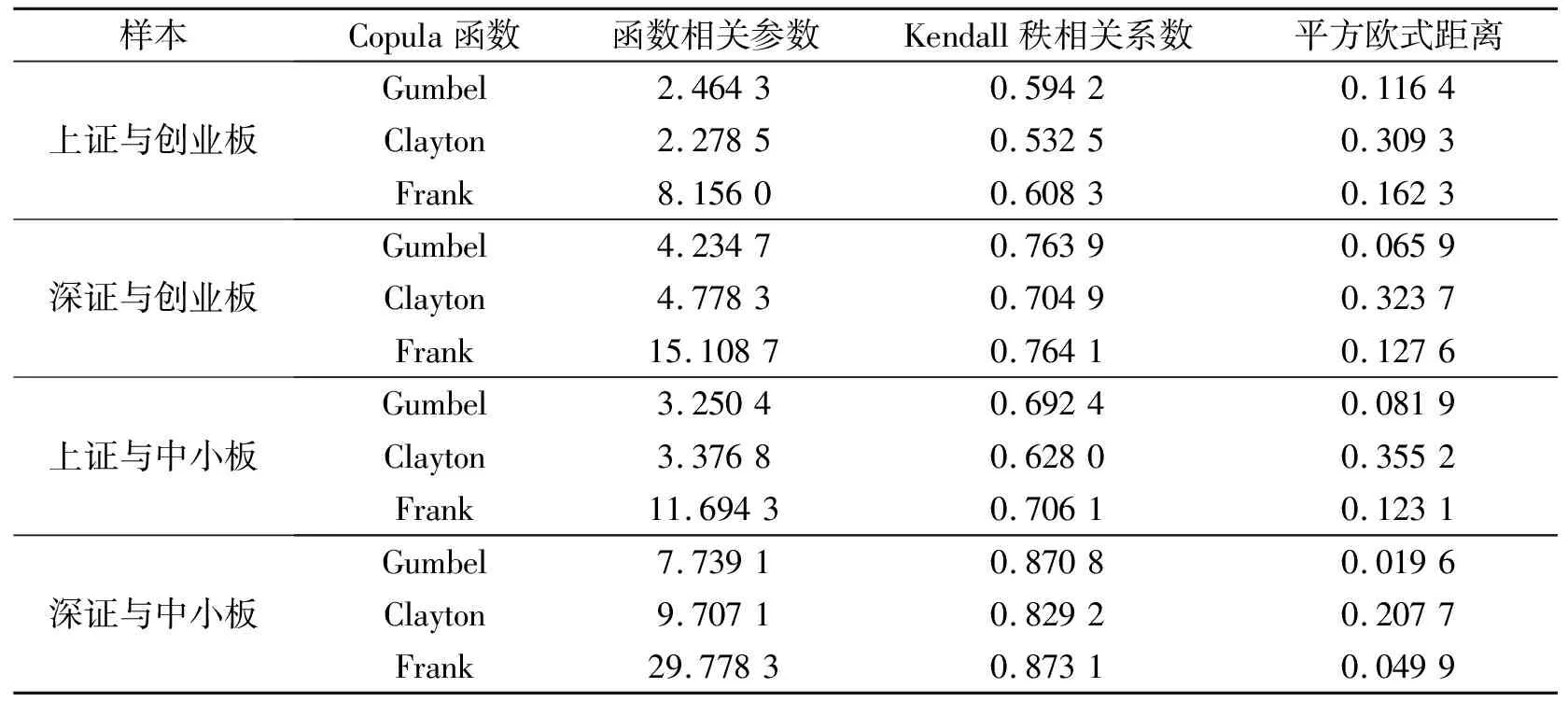
表3 Copula函数的参数估计结果和平方欧式距离

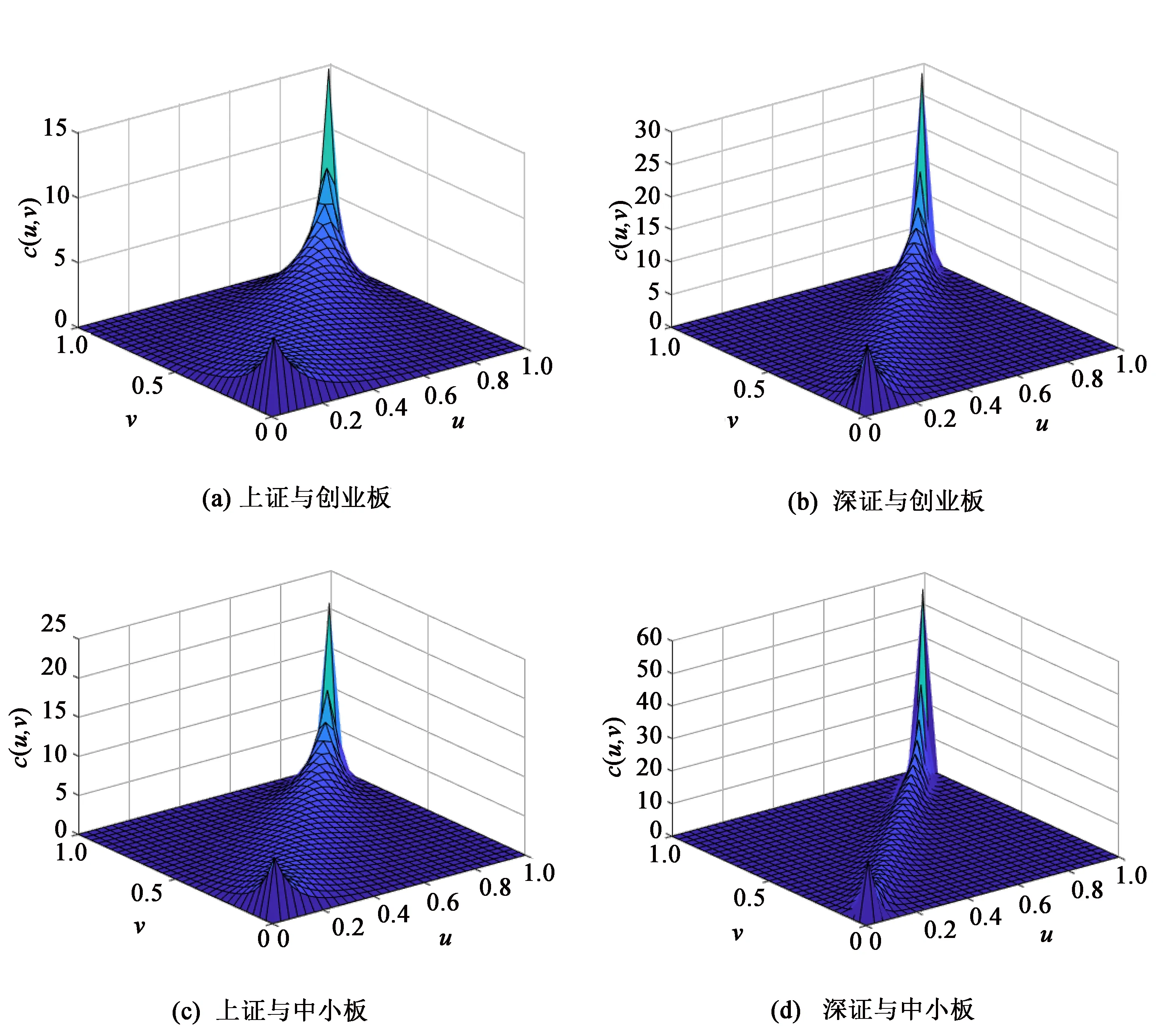
图3 二元Gumbel Copula密度函数图

3 小结

本文利用Archimedean Copula-EGARCH模型对上证综合指数和创业板指数、上证综合指数和中小板指数的相关性及深圳成分指数和创业板指数、深圳成分指数和中小板指数的相关性进行了分析。综合发现，如果上海、深圳股市发生大幅波动，会导致创业板股市、中小板股市发生协同波动，但是如果上海、深圳股市发生大幅下跌时，对创业板、中小板的冲击更强，而创业板、中小板对于深圳股市的波动更为敏感，这对于金融风险管理和金融投资都有指导意义，投资者可以根据股市之间的相关性分析进行风险度量，做出合理决策，调整资产配置，从而获得更多的利益回报。