气浮支承式触针测量系统径向动态性能研究*

（华中科技大学机械科学与工程学院，武汉 430074）

表面质量对机械零件的工作精度、摩擦磨损、润滑、密封等性能有很大的影响，在生产科研中需要用表面形貌测量仪器准确可靠地测量工件表面，分析表面特性，从而优化结构设计，提高零件的工作性能。

触针式表面形貌测量的动态特性好，测量精度高，对测量环境要求相对较低，在实际工程中应用广泛。传统的触针式表面测量仪采用杠杆式触针结构，触针的实际运动是绕杠杆支点的转动，而非直线运动，因此不可避免地会产生非线性误差，需要进行非线性误差补偿。英国泰勒公司研制的Form Taylor PGI测量仪采用标准球进行拟合补偿非线性误差，但拟合算法对非线性误差补偿的精度影响较大[1–2]。范一保等[3]通过合理安装传感器角度实现了非线性误差二次消除，而传感器的安装存在误差，会对测量结果引入新的误差项，补偿精度有限。

气浮轴承具有无摩擦、运动平稳、回转精度高等特点，在精密运动机构、精密加工主轴等领域广泛应用，能够降低运动摩擦阻力和功耗，实现轴系的高速旋转，提高加工精度和加工效率[4–6]。2009年英国国家物理实验室（NPL）[7–8]研制的可用于三维可溯源测量的空间形貌测量仪，将气浮轴承用于表面形貌测量仪中触针位移的支承，实现垂直方向测量不确定度5nm。2011年德国联邦物理技术研究院（PTB）[9]研制的二维表面形貌测量仪也采用了气浮触针式位移传感器，气浮轴承对触针的支承性能决定了测量精度和测量效率，针对表面测量过程中触针轴要求高精度高速直线运动，需要分析气浮触针位移传感器的支承特性。

国内外学者主要对机床主轴，特种电机等方面应用的气浮轴承特性参数进行了深入的研究。张建波等[10]针对单节流孔静压气体止推轴承，提出了一种节流孔系数计算方法，使气浮轴承的承载力计算结果与原方法相比精度提升8%；武静等[11]研究了节流孔出口和均压腔出口圆角对气浮轴承振动特性的影响，验证了圆角结构对振动的抑制作用；Chang等[12]通过比较计算机流体动力学(CFD)计算的气浮轴承的承载力和雷诺方程计算的承载力，研究了节流孔系数的确定方法，试验结果表明节流孔系数的大小受膜厚和节流孔直径影响，而外界供气压力和供气孔外部结果对节流孔系数基本无影响。目前尚未有气浮触针位移传感器的支承特性分析。

本文针对一种气浮触针式测量传感器，建立了气浮支撑式触针测量系统的运动模型，并对气浮轴承的支撑特性和测量系统的动静态特性进行分析，研究了影响气浮支承径向动态性能的因素，进行了径向刚度和动态参数的理论仿真模拟；根据动态模型搭建了气浮支承式触针测量系统试验装置，并通过该试验装置获取测量系统的径向动态特性，验证运动模型的可靠性，为气浮触针位移传感器的设计提供理论依据。

气浮触针式位移传感器的原理

1 结构分析

气浮触针式表面测量系统主要包括气浮触针式位移传感器、运动工作台、控制电路和软件系统，如图1所示。气浮触针包括触针轴、气浮支承、电磁力控制装置和激光干涉计量装置，气浮支承为触针轴提供径向支承，电磁力控制装置则可控制触针轴的测量力，激光干涉计量装置计量触针轴的位移。测量时触针轴跟随被测表面的起伏而上下移动，激光干涉计量触针轴的位移，从而获得被测表面数据，因此测量系统的测量精度和性能主要取决于气浮触针式位移传感器。

激光干涉计量装置基于迈克尔逊干涉原理，触针轴上反射镜的移动将使得光程差改变，从而引起干涉条纹的变化，位移距离L=Nλ/2。其中，λ为光波长，本系统采用λ=635mm的激光器，N为激光干涉条纹移动数。光电探测器接收到干涉条纹信号之后对其进行差分放大处理，将光信号转换为相位差为90°的正余弦电信号，电信号经过调理处理并进行四细分计数，最后对1/4周期内的电信号进行软件细分计数。采用12位±5V软件细分技术，在不考虑触针轴支承误差的前提下，位移传感器理论分辨力为：δ=(λ/2)×(1/4)×(1/2028)=0.039nm 。

气浮支承对触针轴的支承作用主要通过触针轴与气浮孔壁面之间的空气压力。在测量过程中相关作用力下，要减小运动误差对测量精度的影响，确保触针轴的稳定性，需要对气浮支承的结构参数进行优化设计，分析气浮支承的性能特性。

2 气浮支承特性

在气浮支承的设计中，承载力和刚度是主要的性能分析指标。节流器控制着进入润滑间隙的气体，产生压降，使气膜具有一定的承载能力，是结构设计中最关键的部件。小孔节流器承载能力较好，加工方便，本系统中的气浮支承采用小孔节流装置，图2所示为气浮支承的小孔节流示意图。

图1 气浮触针式表面测量系统的结构示意图Fig.1 Structure diagram of air bearing stylus surface measurement system

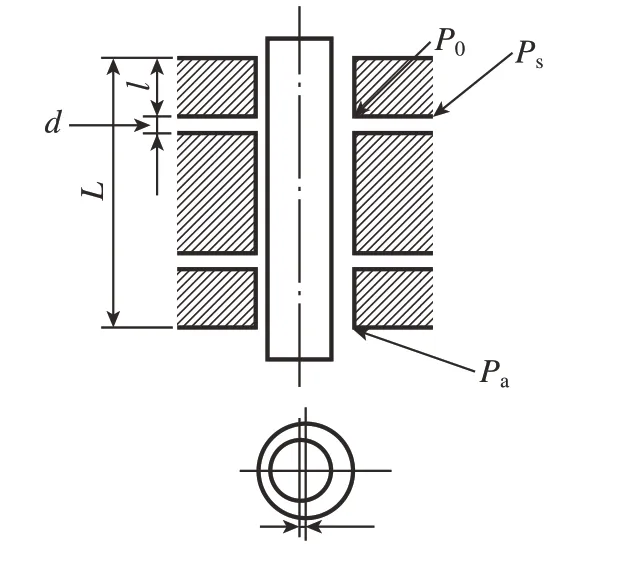
图2 小孔节流示意图Fig.2 Schematic diagram of orifice throttling

若触针轴在测量力的作用下产生偏心，偏心距为e，气浮支承长度为L，两节流孔到端面的距离l，供气压力采用Ps，节流孔出口压力P0。在支承壁面上安排有双排进气孔，均布排列，数量共为4个。

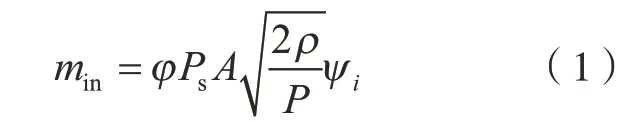
其中，A为节流孔的截面面积；P为工作压力；ρ为供气密度；φ为流量系数，目的是为了考虑到气体流量理论值和实际值的差异，φ一般取0.8。ψi为流量函数，在不同情况下，ψ的取值也会不同，其取值为

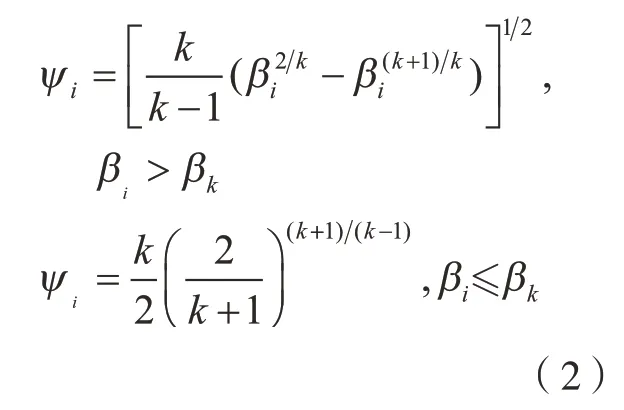
其中，k为气体的等熵指数，对空气取值1.408；，压力比。

假设气体为无惯性的稳态流动，结合适用于静压径向空气轴承的Navier–Stokes方程和质量连续方程，可解得流出支承间隙的质量流量为：

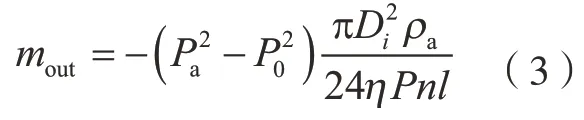
其中，d为轴径；Di为气膜厚度；ρa为空气密度；n为节流孔数量；η为空气黏度。气体为等温层流流动时的状态方程为。根据流量平衡min=mout，可得到关于流出节流口的压力值P0。

可以通过二分法迭代计算出每个节流孔的出口压力P0。

轴与支承轴线产生距离为e的偏心后，轴与支承壁面间的气膜就会发生变化，且气膜厚度与轴向位置无关，而只与周向位置相关。气膜厚度在轴偏心情况下的分布呈余弦规律，则可以表示为：其中，h0为轴与支承壁面的间隙；ε为偏心率；α为偏位角；0°时为气膜厚度最大处。根据式（4）计算的节流口压力P0，结合节流孔的Reynolds方程[14]可以计算出气膜压力分布。

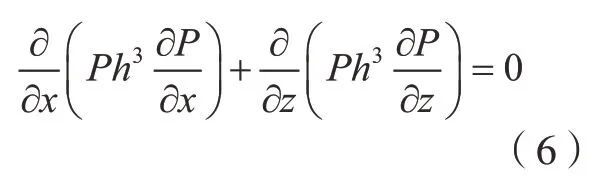
将气膜展开成平面状态，由于节流孔的对称性，只考虑单排下的连续压力分布并作周向展开，则式（6）展开可得：

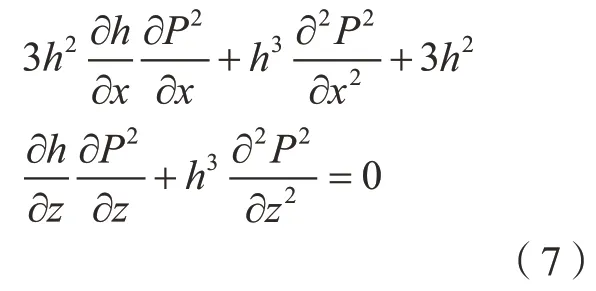
由于气膜厚度在z向保持不变，即∂h/∂z=0，按照有限差分法将网格m×n进行划分并设置边界条件：（1）大气边界P（:，Z（1））=P（:，Z（n））=Pa；（2）周期边界P（X=m+1）=P（X=1）；（3）对称边界P（X=i+1）=P（X=m–i）。结合P0，可以计算各处压力分布P，计算模型的参数取值，见表1。对偏心率为0和0.5下的气浮支承压力分布进行求解，得到压力分布曲线如图3所示。

由此可知，气浮支承压力分布也随着偏心率的不断增加而不断变化，其中节流孔的压力分布变化尤为突出，支承各节流孔处的压力在周向从中间向两边逐渐减小，而且随着偏心率的增加这种趋势也越来越明显。

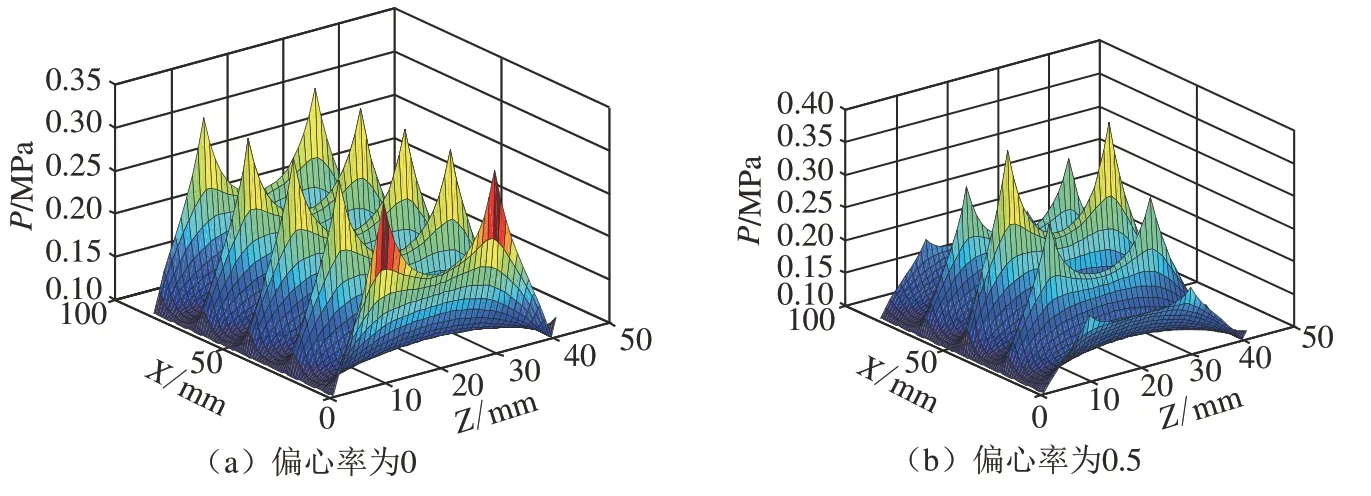
图3 偏心率为0和0.5时的压力分布Fig.3 Pressure distribution at eccentricity 0 and 0.5

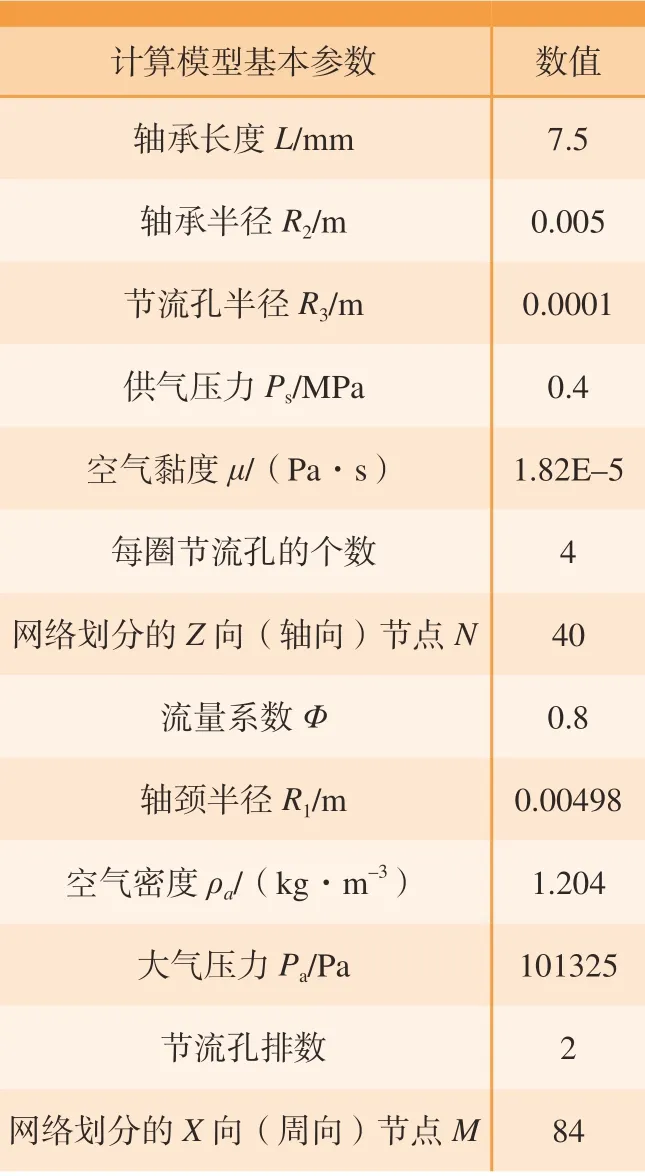
表1 模型参数计算Table 1 Calculation of model parameters

假设触针轴在x轴方向偏心距从e1到e2，偏位角α从α1到α2，由于偏心距很小，认为α1=α2=α。径向承载力可以通过对压力分布进行积分得到。

在不同偏心率下，计算得到的气浮支承的承载力与偏心距F–e曲线，如图4所示。当触针轴发生偏转时，气浮支承的承载力变大，能够使触针轴恢复到平衡状态。

气浮支承的径向动态性能分析

1 运动学模型

测量过程中由于触针轴与被测表面之间的作用力会使得触针轴发生偏斜，使触针针尖在径向和轴向都产生位移误差，影响激光干涉计量装置的可靠性，可能会使测量数据失真，因此要求触针轴在径向上有足够的刚度和较好的动态响应，以保证测量精度和测量效率。

气浮支承式触针位移传感器的受力情况如图5所示，Fe为气浮支撑产生的径向支撑力；R为电磁悬浮线圈的电磁力；G为触针轴所受的重力；F为被测表面与触针接触产生的作用力；Fx和Fy为F的水平分力和竖直分力；F0为预压位移产生的作用力；a为触针轴与被测表面接触点到中心到触针轴质心的距离；b为触针轴质心到气浮支撑中心的距离。测量时，这些力满足条件（1）水平方向：Fe=Fx；（2）垂直方向：R+Fy=G。

触针轴在径向上随水平接触分力变化发生偏转，可以看作触针轴随表面特征的一种响应。当触针轴径向受力偏转时，将触针轴质心看作支点，可将气浮支承式触针位移传感器等效为绕质心旋转的质量弹簧阻尼系统，令m为等效质量，k为等效刚度，c为等效阻尼，如图6所示。

图4 不同偏心率下的承载力Fig.4 Bearing capacity under different eccentricities

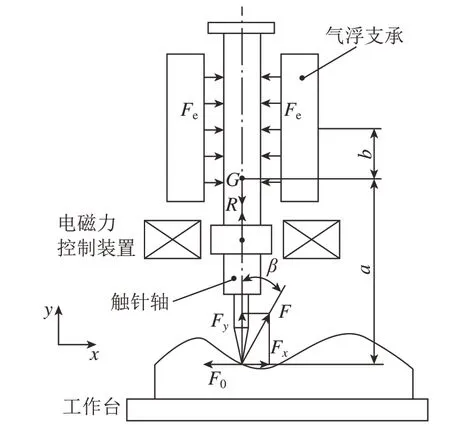
图5 气浮支承式触针位移传感器的受力简图Fig.5 Force diagram of air bearing support stylus displacement sensor

图6中，kb2φ(t)为测量力矩；φ(t)为触针针尖的转动角度；cb2φ˙(t)为阻力矩；φ˙(t)为触针针尖的角速度；J为触针轴的转动惯量；˙˙φ(t)为触针针尖的角加速度，可以得到受力平衡的关系式为：

设触针与被测表面分离时触针轴角度为φf，角速度为φ˙f，令Fx=0，求解式（9）可得触针轴偏转角度为

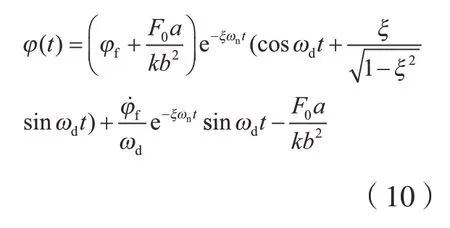
可见运动角度φ(t)的幅值有3项，两项正余弦叠加的振荡曲线和一项预压位移的偏转。刚度k和阻尼c分别可以用固有频率和阻尼比来表示，所以振荡项部分除分离起始点外，最重要的就是与固有频率ωn和阻尼比ξ有关；偏转项与预压力F0和系统刚度有关。刚度k和阻尼c可以用固有频率ωn和阻尼比ξ表示。不同阻尼比和不同固有频率对触针响应曲线的影响如图7、8所示。可以看出，触针失稳现象可以看成时一种随时间变化的衰减振动曲线，在保证刚度k的情况下，应尽量提高ωn和ξ，以减少触针轴响应时间。

图6 气浮支撑式触针测量系统的受力模型Fig.6 Force model of air bearing support stylus measuring system

2 模态参数识别

本文采用自由衰减法进行模态识别法，利用已有的自由振动波形函数求出该系统的阻尼频率与阻尼比，再利用阻尼频率与固有频率的关系，进行模态参数识别。该识别方法对于单自由度模态参数识别系统操作简单、数据直观、应用广泛。

模态识别首先对信号采集并滤波，通过傅里叶变换确定信号的主频率和噪声信号的频率，把高频噪声信号的幅值置零，再通过傅里叶拟变换成时域图，得到滤波后的振动曲线，滤波后去除高频噪声的信号，保留低频信号。对于滤波后的信号数据，先用峰值估算出标准振动方程的参数值作为初始值，采用标准衰减曲线最小二乘参数拟合得到比较精确的参数值，拟合曲线的方程为

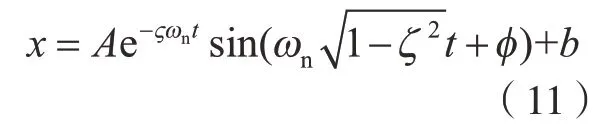
由响应曲线得到的拟合曲线如图9所示。

获得拟合曲线后对曲线进行寻峰，获取波峰幅值Ak(k=1，1，2，3，…)，根据波峰幅值可计算衰减系数a为

则固有频率ωn和阻尼比ξ为

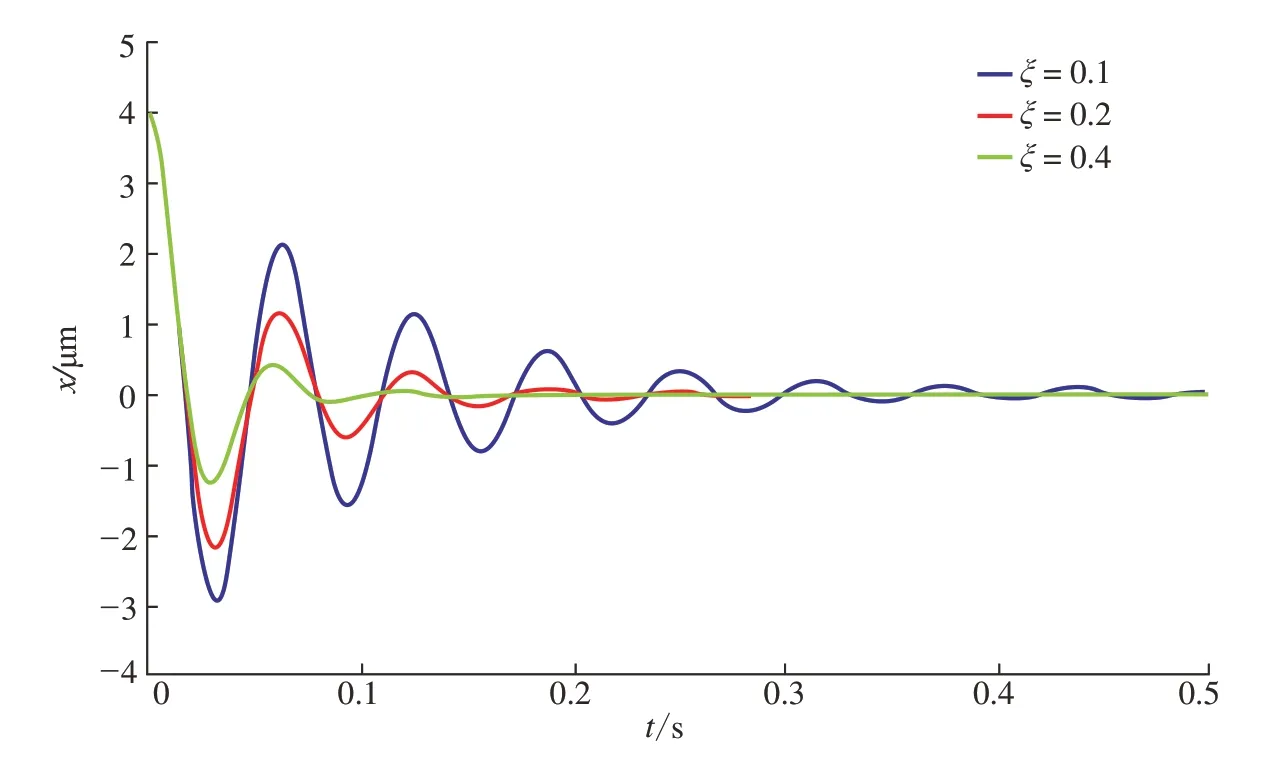
图7 ωn=100rad/s时不同阻尼比对触针响应的影响Fig.7 Influence of different damping ratios on response of stylus when ωn=100rad/s

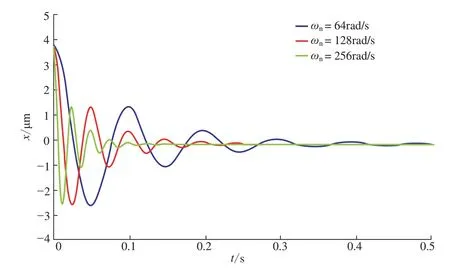
图8 ξ=1.5时不同固有频率对触针响应的影响Fig.8 Influence of different natural frequencies on response of stylus when ξ=1.5

图9 响应曲线的拟合分析Fig.9 Fitting analysis of response curve

试验测试和分析

1 传感器径向测试试验

测试传感器径向响应特性的试验装置如图10所示。为了得到触针轴的径向动态响应参数，需要对触针针尖施加激励，检测触针轴下端的水平位移Δx，根据几何尺寸关系转为触针轴针尖的响应曲线。测试试验中选择KEYENCE生产的LK–G3000高精度激光位移传感器进行测量，测量精度达到0.1μm，重复精度0.05μm，最小采样周期20μs。固定在电机上的斜面以恒定的快速脉冲激励模拟测量过程中的突变表面。

测量得到触针针尖的响应曲线如图11所示。对数据进行滤波、曲线拟合、寻峰和求取固有频率及阻尼比，拟合结果如表2所示。

在持续测量过程中，物体表面给予触针持续的水平方向压力变化，对于机加工的周期性表面，力随位移呈周期性变化，周期性的激励可以展开成简谐激励的叠加，所以由外部持续激励力引起的振动可以看成是有阻尼质量–弹簧系统受迫振动，为了避免引起共振，应当使频率比小于并远离1，即触针的扫描频率应该低于系统固有频率，此时响应振幅与静位移相同；另外考虑到扫描过程中触针能够及时恢复到平衡状态，与到达稳态的响应时间Tstable=8ms有关，扫描频率fscan<1/Tstable=125Hz，略低于杠杆式触针扫描频率fscan=150Hz[15]。考虑到扫描频率与传感器结构参数有关，如触针轴质量、支承结构的刚度等，以后可以对传感器结构进行优化设计，提高传感器的扫描频率。

2 表面形貌测量试验

研制的气浮触针式表面测量试验装置如图12所示，用表面粗糙度Ra=0.8μm标准多刻线样板对测量系统的测量特性进行试验验证。

在测量试验中，测量速度为v=0.1mm/s，采样长度为1.3mm，采样间距为5μm，扫描频率为fscan=20Hz，测量结果无飞针现象，参数评定的结果为Ra=0.7936μm，相对测量误差为0.8%。测量数据如图13所示。

结论

本文介绍了气浮触针式位移传感器的测量原理，对气浮支承的结构参数进行了设计，并对该传感器的径向动态特性进行了分析和测试。

图10 传感器径向响应特性测试试验装置Fig.10 Experimental device for measuring radial response characteristics of sensors

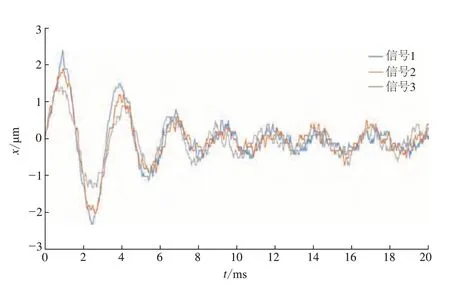
图11 触针轴动态响应信号Fig.11 Dynamic response signal of stylus shaft

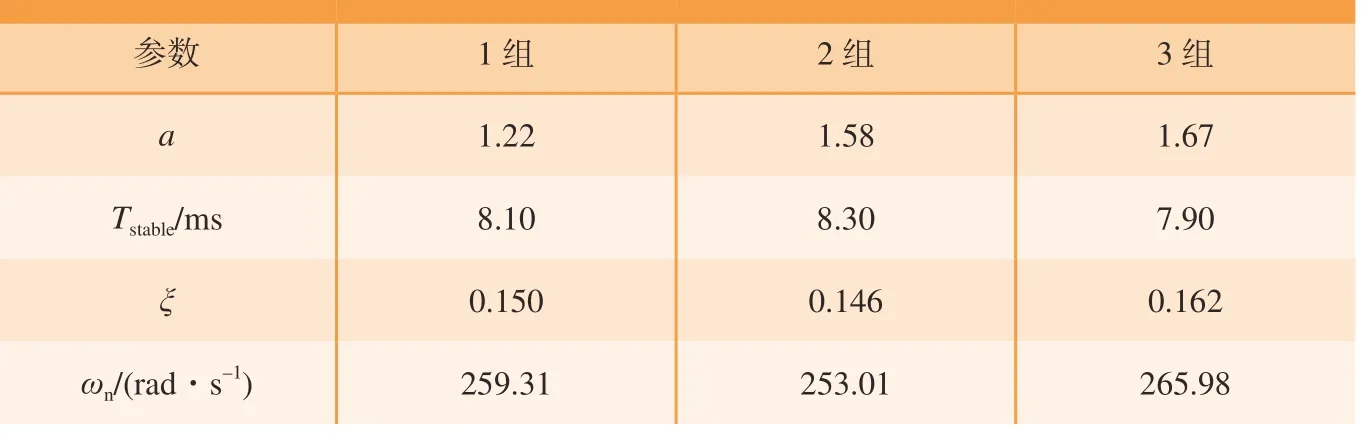
表2 振动曲线模态识别结果Table 2 Modal identification results of vibration curve

图12 气浮触针式表面测量试验装置Fig.12 Air bearing stylus type surface measurement test device

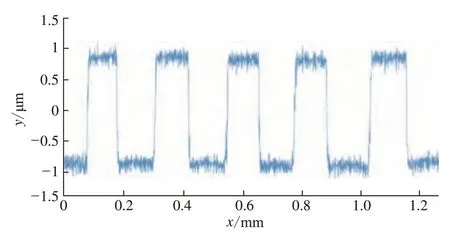
图13 v=0.1mm/s时标准多刻线样板的表面形貌测量结果Fig.13 Measurement results of surface topography of standard multi reticle template when v=0.1mm/s

（1）气浮支承的结构有效避免了非线性误差，提高了测量精度，可应用于测量表面粗糙度等形貌测量方面。

（2）通过动态特性试验测试和分析，本文研制的气浮触针传感器的最大扫描频率为125Hz，略低于杠杆式触针位移传感器，以后可以通过对气浮触针位移传感器结构的优化设计提高扫描频率。

（3）利用搭建的气浮触针式表面形貌测量系统对标准样板进行了测量试验，相对测量误差为0.8%。