基于PFC3D的路基土细观特征数值模拟研究

刘晓东

(中铁十九局集团第三工程有限公司，辽宁 沈阳 110136)

0 引言

路基是公路工程中的重要组成部分，路基结构的稳定性将直接影响整个公路系统的正常运行。路基土作为路基结构中的填充材料，其力学性质尤为关键。传统室内试验仅能对路基土的宏观力学参数进行分析，而土体内部裂隙及颗粒间的接触状态很难得到。因此，本文结合PFC3D对路基土的细观力学特性进行研究。

近年来，我国学者对路基土进行了大量研究，成果颇丰。王子寒等[1]基于PFC3D对不同形状的粗粒土的接触状态进行了研究，通过接触试验分析了法向、切向的接触力学特性。刘小文等[2]通过颗粒流数值模拟软件建立了非饱和土的直剪试验数值模型，并对不同固结力及基质吸力下的非饱和土进行了数值模拟研究。周凤玺等[3]基于颗粒流方法，采用Hill模型进行了非饱和土的三轴试验模型，并对不同围压、不同吸力下试样的应力-应变特征进行了分析。毛海涛等[4]采用PFC3D对紫色非饱和土进行了不同围压及含水率下的数值模拟研究，并与室内试验结果进行了对比。杨升等[5]基于PFC3D建立了砂土剪切试验模型，分析了新疆地区砂土的体积变化及剪切带变化情况。

综上分析，已有研究对路基土进行了较为详细的研究。本文在已有研究成果的基础上，结合颗粒离散元软件PFC3D对辽宁某在建公路路基土进行数值模拟研究，分析不同围压作用下土体内部的裂隙扩展及颗粒间接触力的分布情况，为路基土的细观力学性质提供可靠的理论依据。

1 数值模型建立与细观参数标定

1.1 三轴数值模型建立

本文采用三维颗粒流数值仿真软件(PFC3D)建立高80 mm、直径39.1 mm的标准试样，颗粒间接触本构模型采用线性黏结模型。加载方式采用位移控制进行加载，首先圆柱墙体和上下加载板墙体同时以0.02 mm/s的加载速率对试样匀速施加围压，待围压稳定后，圆柱墙体保持恒定，上下加载板继续以0.02 mm/s的加载速率对试样进行加载，方向相反。试验结束条件可根据轴向应变进行控制，通常认为轴向应变达到15%时认为试样完全破坏。加载过程中，PFC程序将自动记录模型应力应变数据、裂纹扩展状态、裂纹数目及能量等相关试验数据。为分析不同围压下路基土的裂纹扩展状态及颗粒间接触力的演化规律，本文设置围压分别为50、100、150和200 kPa。

1.2 细观参数标定

在PFC数值模型中，其宏观力学行为是由细观参数所决定的，包括颗粒大小、颗粒间接触模量、法向和切向黏结强度、颗粒间黏结刚度比等，不同的细观参数将直接影响数值试验的峰值强度、弹性模量等宏观力学参数。为了尽量贴近室内土体三轴压缩应力-应变曲线，需对PFC数值模型进行细观参数标定，使数值模拟结果尽可能反应真实试验条件下土的力学行为。路基土室内单轴试样取自施工现场，通过制样模具制得高80 mm、直径39.1 mm的圆柱试样。采用GDS对制备好的土体进行单轴压缩试验，试验控制条件与PFC数值试验保持相同，获得土样室内试验宏观力学参数，并以此为基础反复进行单轴压缩数值试验，最终获得满足室内试验结果的细观参数，如表1所示。

表1 路基土细观参数

2 数值试验结果分析

2.1 应力-应变曲线分析

图1为不同围压下路基土的数值试验三轴压缩应力-应变曲线。从图1可以看出，当围压较低时，试样表现为应变软化，随着围压的逐渐增大，试样逐渐向应变硬化过渡。且随着围压的增大，曲线波动性逐渐增强，其原因是颗粒间相对滑动后形成新的接触面，继续承担荷载。以围压100 kPa为例，应力-应变曲线大体可分为三个阶段，包括线弹性阶段、塑性屈服阶段和应变硬化阶段。其中，塑性屈服阶段还可细分为裂隙稳定发育阶段和裂隙不稳定发育阶段。

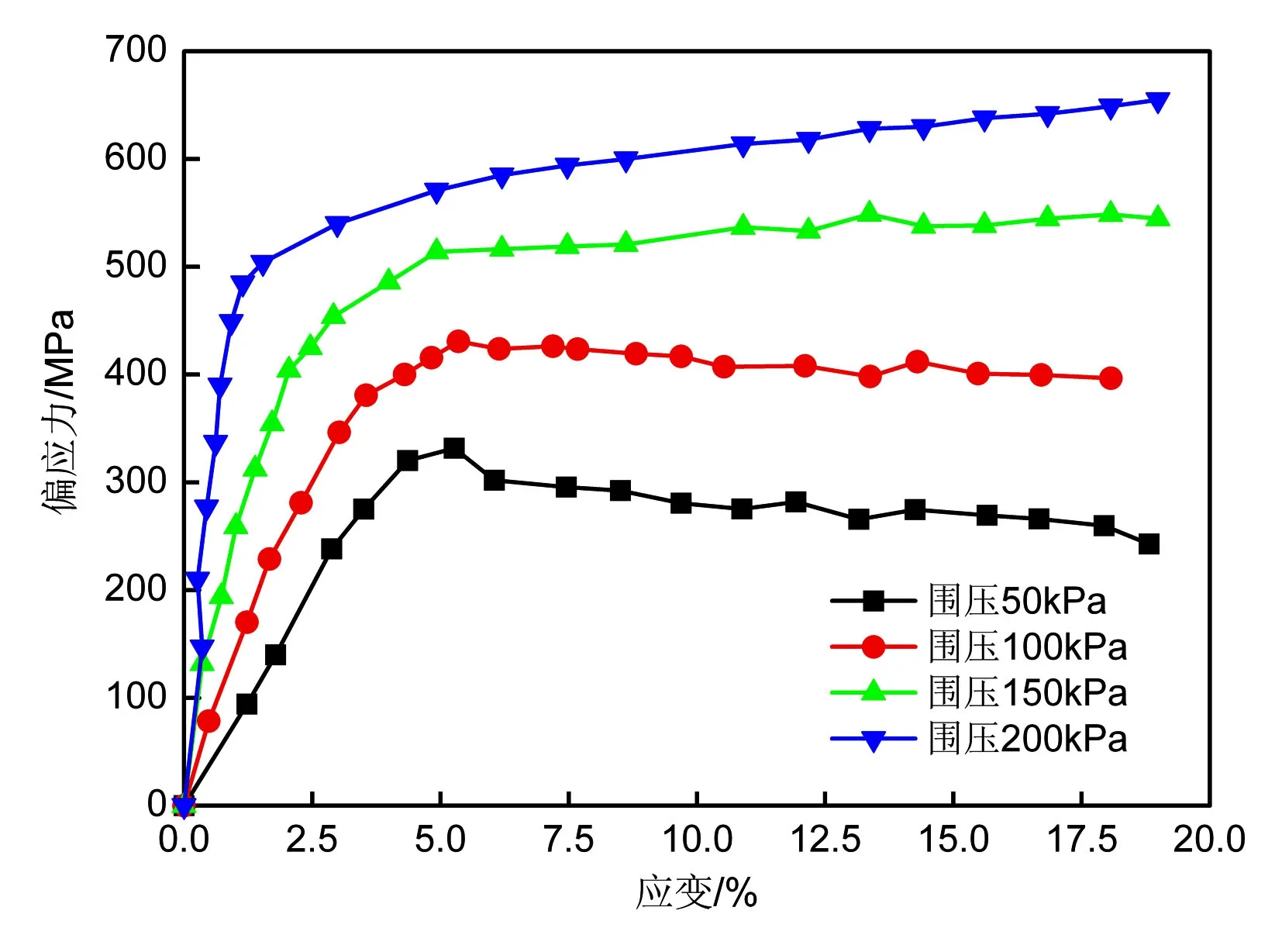
图1 砂岩数值试验三轴压缩应力-应变曲线

2.2 裂隙发育规律分析

图2分别为不同围压条件下试样内部裂隙发育情况，图中蓝色为张拉裂隙、红色为剪切裂隙。从图中可以看出，不同围压条件下，试样的裂隙扩展规律大体相同，其中张拉裂隙几乎布满整个试样，而剪切裂隙则主要在剪切带附近扩展，剪切带与轴向加载方向夹角约为60°。

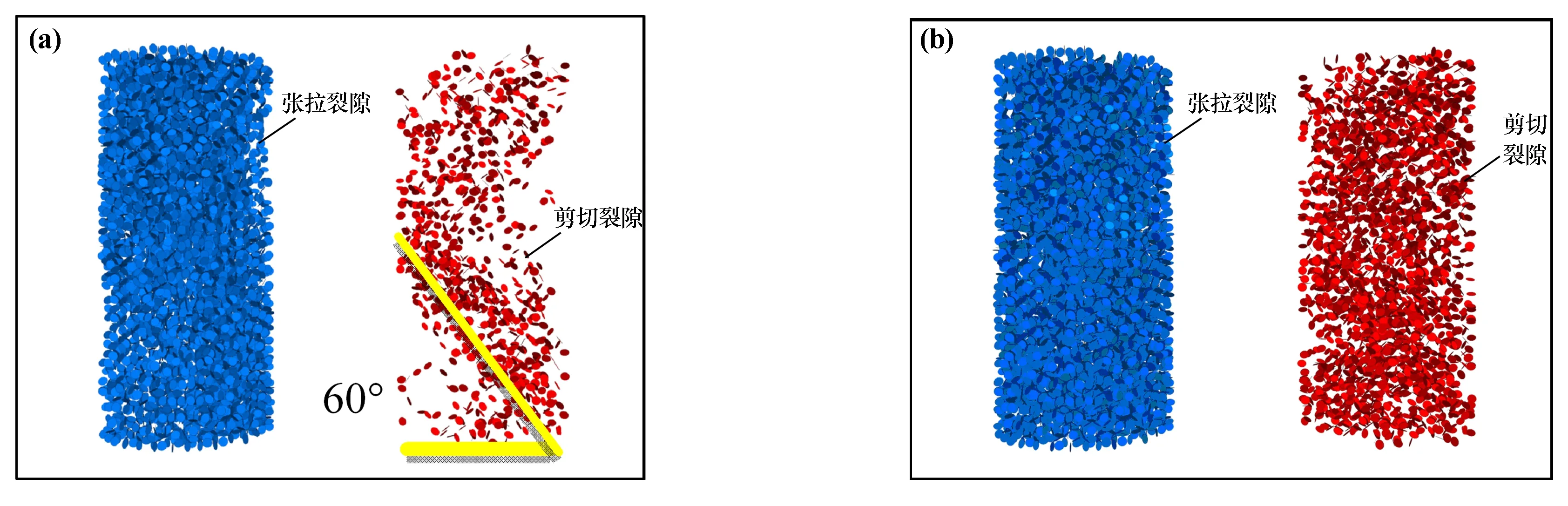
图2 不同围压下试样内部裂隙发育情况

根据试验结果，绘制张拉裂隙和剪切裂隙发育条数随围压分布曲线，如图3所示。从图3中可以看出，随着围压的逐渐增大，试样内部的拉伸裂隙和剪切裂隙均逐渐增多。围压从50 kPa增至200 kPa，拉伸裂隙变化增幅较小，剪切裂隙增幅较大。在不同围压情况下，拉伸裂隙几乎布满整个试样，而剪切裂隙则不同拉伸裂隙。在低围压情况下，剪切裂隙主要分布在剪切带附近，其他位置零星分布，在高围压情况下，拉伸裂隙几乎布满整个试样。可见，随着围压的逐渐增大，土体内部裂隙显著增多，破碎程度逐渐加重。采用Origin软件对图中数据进行最小二乘拟合，发现拉伸裂隙与剪切裂隙均随围压呈指数函数递增，拟合相关系数均在0.95以上，即两种裂隙与围压之间具有良好的相关性，且随着围压的逐渐增大，两种裂隙增长速率逐渐趋缓。

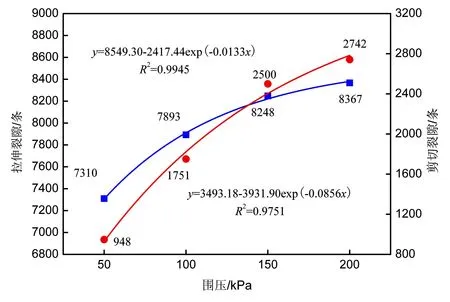
图3 裂隙数量随围压分布曲线

2.3 接触力分布规律分析

图4为围压200 kPa下颗粒间接触力分布玫瑰图。可以看出，法向接触力在90°和270°左右两侧近似上下对称分布，其中最大法向接触力在90°左右两侧分布，270°处接触力略小于90°，最大切向接触力则主要分布在60°左右两侧，而在120°、240°和300°处均出现明显接触力增大，但与60°相比略微偏小，且切向接触力近似呈中心对称分布。根据统计结果，不同围压下颗粒间法向接触力与切向接触力的分布规律大体相同，随着围压的逐渐增大，法向接触力和切向接触力均呈逐渐增大趋势。当围压50 kPa时法向接触力最大值为300.8 kN，切向接触力最大值为59.6 kN，当围压分别为100、150和200 kPa时，法向接触力最大值分别增长了23.27%、55.94%和92.99%，切向接触力最大值分别增长了36.02%、47.40%和84.65%。可见，围压对颗粒间接触力具有显著的促进作用。

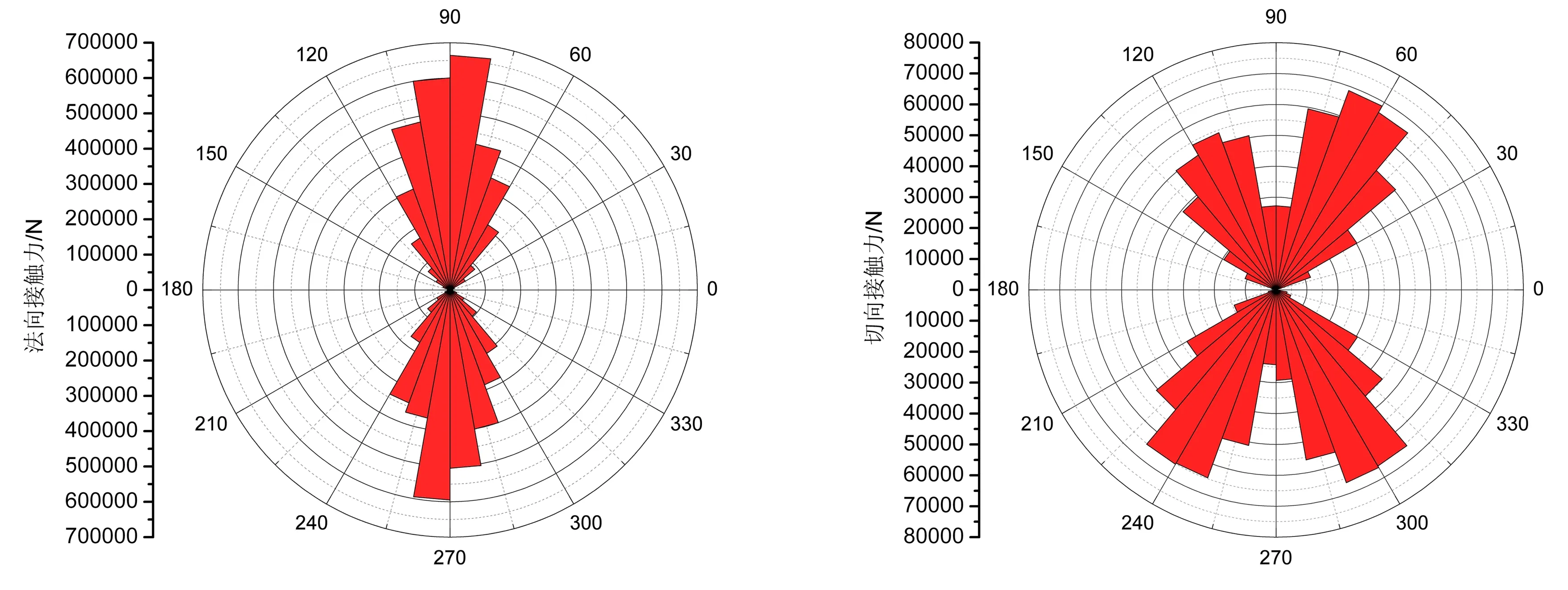
图4 围压为200 kPa时颗粒间接触力分布玫瑰图

3 结论

(1) 当围压较低时，试样表现为应变软化特征，当围压较高时，试样表现为应变硬化特征，且随着围压的增大，曲线波动性逐渐增强。

(2) 随着围压的逐渐增大，试样内部裂隙均逐渐增多。其中，拉伸裂隙增幅较小，剪切裂隙增幅较大。采用Origin软件对图中数据进行最小二乘拟合，发现拉伸裂隙与剪切裂隙均随围压呈指数函数递增，拟合相关系数均在0.95以上，即两种裂隙与围压之间具有良好的相关性。

(3) 随着围压的逐渐增大，法向接触力和切向接触力均呈逐渐递增趋势。当围压50 kPa时法向接触力最大值为300.8 kN，切向接触力最大值为59.6 kN，当围压分别为100、150和200 kPa时，法向接触力分别增长了23.27%、55.94%和92.99%，切向接触力分别增长了36.02%、47.40%和84.65%，表明围压对颗粒间接触力具有显著的促进作用。