“金融加速器效应”抑或“理性资产价格泡沫效应”

张蕊 郭潇蔓 申程程

摘 要： 现阶段中国经济面临下行压力，资产价格已到高位，探寻不同金融和经济环境下货币政策如何兼顾“稳增长”和“防风险”显得非常必要而紧迫， 而“金融加速器”理论和“理性资产价格泡沫”理论对货币政策的选择提供了矛盾的理论依据。利用主成分分析法构建了包括股票、房地產、债券和基金的中国金融资产综合价格指数，以2006年第四季度至2020年第一季度为研究期，基于TVP-SV-VAR模型研究了货币政策、资产价格与经济波动三者之间的时变关系。研究发现：在正常经济环境中，中国存在“金融加速器效应”，但资产价格达到高位之后，“理性资产价格泡沫效应”显现，即资产价格随着利率的提高而上升;随着时间推移和中国资产价格泡沫程度的提高， “利率下降→宏观经济增长”这一政策传导渠道的有效性逐渐降低;资产价格上涨短期内推动经济增长，严重泡沫时可能抑制经济增长;建议目前宏观调控方向为“扩信用，稳货币，松财政”。

关键词：货币政策;资产价格;经济波动;TVP-SV-VAR模型;时变效应

文章编号：2095-5960（2021）06-0036-12;中图分类号：F832.5;文献标识码：A

一、引言

在过去30 余年的世界经济实践中，货币政策不仅作为重要的宏观调控手段影响着实体经济的周期性，同时又与金融稳定密切相关。Mishkin将货币政策作用于实体经济和金融环境的传导渠道定性化地归为四类：利率渠道、信贷渠道、资产价格渠道和汇率渠道。[1]近年来居高不下的杠杆率更是扩大了货币政策通过资产价格和信贷渠道对实体经济和金融稳定的影响。金融危机史表明，金融危机往往出现在金融资产价格的高峰附近，金融危机的暴发带来严重的信贷收缩和断崖式的资产价格下跌，而资产价格下跌又会导致信贷收缩，二者螺旋式的相互作用会对实体经济造成巨大的产出损失。2008 年美国金融危机之前，产出缺口和通货膨胀一直都被政策当局认为是货币政策应该关注的核心，许多国家的中央银行都忽视了资产价格的波动。金融危机之后，货币政策如何更有效地应对资产价格的波动及其对实体经济的影响成为近年来学术界和政策当局亟待解决的难题。

自2012 年起，中国经济显露出增速放缓的迹象，2012～2015年，GDP 的平均增长率为7.45%，而2016～2019年，GDP 的平均增长率为6.55%。①    ①根据国家统计局相关数据计算得出。  2020年新冠肺炎疫情爆发和蔓延，中国经济下行压力进一步加大。近年来扩张性货币政策作为稳定经济增长的重要调控手段使得中国一直处于较低的利率环境，2020年继续实施了多项常规和非常规的宽松货币政策，房地产和其他金融资产价格泡沫以及系统性金融风险有可能会进一步增加。因此，如何评估宽松的货币政策对金融资产价格的影响和对实体经济的提振作用，以及如何调整货币政策，在实体经济增长与金融稳定之间相机抉择，是一个非常紧迫的问题。

论文的研究贡献在于：第一，多种金融资产价格是货币政策传导至实体经济的重要渠道，但目前绝大部分研究仅采用单一资产价格——股票价格或房地产价格来衡量资产价格。美国股票市场在整个金融市场中举足轻重，仅以股票价格作为资产价格的代理指标，也忽视了房地产和以其为支撑的金融衍生品（次级债）的价格下跌对一国金融体系和实体经济的巨大打击。股票在中国金融资产中占比较小，房地产却具有典型的投资品特征，而且各类债券和基金也逐渐成为重要的金融资产，只采用其中一种资产价格显然难以全面地揭示中国货币政策对资产价格和金融稳定性的影响机制和影响程度。因此，本文选取目前中国主要的金融资产价格——股票、债券、基金和房地产价格，基于主成分分析法构建反映中国整体资产价格态势的金融资产综合价格指数。第二，通过“金融加速器”理论和“理性资产价格泡沫”理论可以发现，在不同的经济阶段和不断变化的金融环境中，货币政策与资产价格、实体经济之间的影响是随时间而变化的。最近几年已有少量实证结果表明货币政策调控与金融市场之间关系受宏观经济周期、杠杆周期的影响，具有相当程度上的时变特征。因此，本文采用具有时变特征的模型——一个带有随机波动率的时变参数的向量自回归模型（TVP-SV-VAR）来考察在不同经济金融环境下货币政策、资产价格与经济波动三者之间相互影响的时变性及其蕴含的政策意义。

二、文献综述与理论假设

（一）理论研究

目前关于货币政策、资产价格和实体经济三者关系的理论研究大多基于两个理论：广义“金融加速器”理论和“理性资产价格泡沫”理论。然而，目前尚未有将二者结合的理论框架和实证模型。

早期货币政策与经济周期的研究中，信贷约束与资产价格都被视作外生。20世纪90年代发展起来的广义“金融加速器”理论首次将货币政策、资产价格和经济周期纳入一个统一的内生框架中，深入研究了货币政策通过资产价格这一渠道对实体经济的影响，特别是这一渠道的放大效应（加速器作用）。但研究重点都是资产价格对信贷周期和经济波动的影响，较少关注经济波动对资产价格的影响。本文更关注二者螺旋式的相互作用机制，并且对其中的非对称性和非线性成分进行更深入地考察。

1.资产价格与经济波动的螺旋式相互作用机制

Bernake & Gertler[2]，Bernanke， Gertler & Gilchrist [3]认为，在信贷市场中贷款企业与金融机构存在信息不对称，因此二者之间存在借贷代理成本，而企业净资产有助于减少借贷成本。他们提出的BGG模型的核心部分在于其创新性的信贷市场局部均衡模型：

假设 Q t，Kj t+1，Nj t+1，Rk t+1，R t+1 分别为第t时期（贷款时期）资本的市场价格、第t+1时期（因为投资和收益都发生于第t+1时期）第j个企业的最优借贷资本数量、企业净资产、企业借贷资本收益率和无风险利率，最优借贷资本应满足以下关系：

Q tKj t+1=ψ E  Rk t+1 R t+1    Nj t+1，当ψ（1）=1，ψ′（·）>0   （1）

令S t=E  Rk t+1 R t+1   为预期的资本贴现收益率，反映了企业信贷成本。式（1）反映了企业的借贷成本与财务状况之间的关键联系：企业的最优借贷规模与企业的净资产成正比，与预期贴现资本收益率成正比。在其他条件相同的情况下，预期资本贴现收益率上升会降低预期违约概率，导致企业承担更多的债务并扩大公司规模。但借贷资本与净值的比率上升，预期违约成本上升，所以企业并不能无限扩张。

更进一步，在金融机构的融资市场上，Gertler & Karadi[4]在BGG模型的基础上，纳入了金融机构内生的信贷约束：金融部门的外部融资规模同企业部门一样也会受到其净资产水平的影响。令 S t，  t 分别是第t期银行的融资规模和杠杆（银行资产与其净资产的比率），银行的最优融资规模应该满足式（2）。若银行杠杆不变，银行融资能力与其净值成正比。

Q tS t=  tN t   （2）

式（1）和（2）提供了银行与企业之间的内生信贷约束以及银行与储户之间的内生融资约束。在信息不对称的条件下，企业的信贷约束和成本由其净值内生决定，银行可用于信贷的融资规模和成本也是由银行的净值内生决定。而企业和银行的净值主要由企业的产出、利润和资产价格决定。

如果正向的货币冲击（扩张性货币政策）或金融冲击、技术冲击等导致产出增长和资产价格上升，企业净值升高，企业外部融资成本下降，企业投资增加。同时由于银行的资产价格提高，银行的融资能力和融资成本也大幅改善，银行流动性增加支持了企业投资扩大。流动性充裕和投资规模扩大进一步推高了资产价格和企业、银行的净值，银行和企业的外部融资进一步扩张，资产价格和产出、投资螺旋式相互推动上涨。

如果实施紧缩性货币政策或发生其他负向的外生冲击如资产价格波动、疫情等，资产价格下跌，企业利润减少、净值下降，外部融资成本上升，不得不缩小投资规模。同时，资产价格下跌会导致银行等金融中介净值减少，杠杆上升。受限于金融监管当局杠杆监管的硬约束，不仅银行创造的内生货币减少，甚至可能会为了达到监管要求，变卖资产，引发资产价格进一步下跌，导致银行和企业净值进一步下降，信贷市场萎缩，资产价格和实体经济同时进入螺旋式下降的恶性循环。此时，货币当局处理信贷市场失灵的关键应为解决信贷需求方的融资困难，遏制资产价格的大幅波动，可以提高企业的外部融资能力，使得企业产出保持稳定。

从理论分析和实践来看，金融加速器效应还有一个重要特征：各种冲击对宏观经济造成的影响是时变的，具有非对称性。比如在经济下行期，企业外部融资环境明显恶化，银行也受到杠杆和流动性的硬约束，金融加速器效应要明显强于经济上升期;[5]对于规模较小的企业，在信贷紧缩时期对资产负债状况影响更为敏感，导致其金融加速器效应也要强于规模较大企业的金融加速器效应。[6，7]

2. 理性资产价格泡沫

与金融加速器理论不同，Gali基于理性资产价格泡沫理论，将资产价格分解为基本面部分和泡沫部分，推导出货币政策和资产价格、经济波动关系的另一种可能：当存在理性资产价格泡沫时，紧缩性货币政策虽然可能导致产出和利润下降，但仍可能会助长泡沫，使资产价格进一步上升，从理论上证明了货币政策与资产价格和经济波动关系的复杂性和情景依赖。[8]

Gali & Gambetti利用局部均衡资产定价模型推演了理性资产价格泡沫环境下货币政策对资产价格的非传统影响机制。 [9]假设在一个经济体中含有风险中性的投资者和无限生命的资产（股票或住房）。在第t时期存在具有时变特征的无风险利率 R t，资产价格为Q t，股利收益为{D t }。在达到理性预期下的均衡时，存在

Q tR t=E t{D t+1+Q t+1}  （3）

将资产价格分解为基本价值部分Q tF和泡沫部分Q tB， 则：

Q t=Q tF+Q tB  （4）

基本价值部分Q tF可由预期的未来股利贴现形成，紧缩性货币政策和产出负向波动都可能通过提高未来的利率预期和减少未来的股利预期降低资产价格中的基本价值部分，与传统理论一致。

Q tF=E t ∑∞ k=1 ∏k-1 j=0 1 R t+j  D t+k   （5）

Q tFR t=E t{D t+1+QF t+1  （6）

式（3）（4）（6）可以得到泡沫部分

Q tBR t=E t{QB t+1}  （7）

E t  QB t+1 Q tB  =R t  （8）

从式（7）（8）看出，与Q tF相反，利率上升将会提升资产价格的泡沫部分Q tB的 预期收益率。 因此，资产价格若已隐含了理性泡沫，提高利率的“逆风而行”货币政策会将资产价格泡沫部分进一步放大。

同时，利率变化还会从另一个渠道来影响资产价格的泡沫部分，该渠道是资产价格泡沫中的不确定新息 {ξ t  }与利率中的意外成分 r t-E t-1{r t} 之間的相互作用。

对式（7）在t-1时期进行对数线性化，同时删除期望算子，得到

q tB=r t-1+qB t-1+ξ t  （9）

其中，q tB、r t-1和qB t-1分别是Q tB、R t-1和QB t-1的自然对数，泡沫部分中的不确定新息{ξ t}是具有零均值的鞅差过程，则对于所有时期t，E t-1{ξ t}=0。{ξ t}与资产价格的基本价值部分关系不确定，可能有关，也可能无关。提高利率对资产价格泡沫的同期影响由{ξ t}与利率中的意外成分r t-E t-1{r t}之间的相互作用决定，可将二者的关系表达为

ξ t=ξ t*+Ψ r（r t-E t-1{r t}）  （10）

其中，{ξ t*}是一个在所有提前期和滞后期中都与利率中的意外成分r t-E t-1{r t}正交的零均值鞅差过程，即对于k=0，±1，±2，±3…都存在E{ξ t*r t-k}=0。资产价格泡沫中的不确定新息与利率中的意外成分之间的关系用Ψ r来表示。假设{r t}遵循的外生AR（1）过程包含利率意外成分ε tr和自回归系数ρ r， 自回归系数ρ r满足ρ r∈[0，1）。经过进一步推导可得泡沫对正向利率冲击的反应：

qB t+k  ε tr =Ψ r+ 1-ρ rk 1-ρ r   （11）

令k=∞，可得

lim  k→∞  qB  t+k  ε tr =Ψ r+ 1 1-ρ r   （12）

当Ψ r取零值时，表明二者之间没有系统性关系，虽然当前泡沫的大小并不能被利率影响，但是泡沫的预期增长率随着利率上升而上升，形成泡沫的永久性增长。

当Ψ r取正值时，结论显然不变，只不过增长率提高Ψ r，泡沫增长更快。

当Ψ r取负值时，由于Ψ r是利率的提升对泡沫的初始影响，为负值。但只要无法保证Ψ r 的取值足够小，随着时间推移，利率的提升仍会导致资产价格泡沫的进一步膨胀。

Gali & Gambetti构建的这个简单局部均衡模型表明：虽然利率上升会缩小住房或者股票等资产的基础价值成分，但是，在大多数情况下，紧缩性货币政策却扩大了房价和股价的泡沫成分。可以发现，“逆风而行”的货币政策是否一定会推高资产价格还具体依赖于资产价格中基本价值成分和泡沫成分的相对大小以及货币政策对二者影响的相对大小。因此，紧缩性货币政策虽然导致产出和利润下降，但可能推高了资产价格，部分抵消了其对信贷市场的负面影响，使得三者之间的关系更趋复杂，需要利用实证方法和具体数据来进一步检验。

（二）实证研究

继Bernanke， Gertler & Gilchrist基于金融加速器理论建立了动态一般均衡模型（DSGE）后，已有不少文献发展了多种DSGE模型实证研究货币政策、资产价格与实体经济之间的相互关系。Nisticò把股票价格的波动因素加入央行跨期消费决策方程中研究股票市场的波动如何传导至实体经济[10]，该研究表明股价的波动同样需要纳入货币政策的考虑中。Kannan 等的研究发现[11]，货币政策在金融加速器的作用下能够显著地推动房地产价格的上涨，不断上涨的房地产价格又持续推高了金融风险，所以，若要兼顾房地产市场和宏观经济的平稳运行，需要采用相机抉择的货币政策。陈诗一采用DSGE模型研究了中国房地产价格波动与货币政策传导的关系，其研究认为：降低社会融资成本不仅能够有效控制扩张性货币政策引起房地产价格泡沫的风险，还能维持宏观经济稳定。[12]高小红和苏玮基于多部门NK-DSGE模型的研究结果表明股价冲击对经济的影响比货币政策冲击对经济的影响更大，且认为中央银行考虑股价波动的货币政策可以有效降低冲击造成经济偏离均衡增长路径的幅度。[13]但目前DSGE模型中大多数方程都进行了线性假定，由此得到的各类脉冲响应函数结果的可靠性仍存在一定的疑问，此问题在资产泡沫高涨或经济下行期更甚。

关于三者关系的时变性研究和理性资产价格泡沫效应的文献多是经验研究。陈继勇等实证研究了在价格极度萧条时期与极度繁荣时期，中国资产价格的流动性特征和其波动的隐含信息，结果发现：货币总量对股票价格的调控效果较好，而信贷总量对房地产价格的调控效果更好，在成功修正资产价格的基础上还能较好地稳定宏观经济环境。[14]闫先东和朱迪星构建了一个多变量的 MSVAR模型，基于滚动周期回归的研究方法发现，在资产价格萧条阶段，资产价格下滑对经济的负面冲击非常显著，“逆风而行”的货币政策很难进行有效的调控。[15]然而在资产价格繁荣阶段，政策干预和流动性驱动的泡沫形成态势比较明显，但对实体经济的正向影响并不显著。Gali & Gambetti、陈浪南和刘劲松分别基于美国和中国的股票市场数据验证了资产价格波动与货币政策利率冲击之间的关系[16]，得出的结论符合理性资产价格泡沫理论。

通过文献梳理可以发现，目前既没有将“金融加速器”理论和“理性资产价格泡沫”理论相融合的理论框架，也缺乏在不同的经济阶段和不断变化的金融环境中同时考虑这两种效应的实证成果。我们采用具有时变特征的TVP-SV-VAR模型确实捕捉和验证了这两种效应在中国不同的宏观经济和金融环境下都是存在的，而且2006年第四季度至2020年第一季度这一时期货币政策、资产价格和实体经济相互影响的时变脉冲响应函数也为货币政策的选择及其实施的时机和力度提供了大量的信息。

（三）研究假设

基于上述的文献梳理，我们提出本文的三个研究假设：

H1：包含房地产、股票、债券、基金的金融资产价格既是货币政策影响经济波动的渠道，也是货币政策和经济波动的结果。

H2：在正常经济环境中，中国存在“金融加速器效应”。货币政策、资产价格和宏观经济波动的关联是非线性的，在经济周期的不同阶段和不断变化的金融环境中，三者之间的关系具有相当强的时变性。

H3：在资产价格达到高位等极端環境下，“理性资产价格泡沫效应”显现，即资产价格反而会随着利率的提高而上升，打破资产价格与经济波动的正反馈，削弱了“金融加速器效应”。

三、实证研究设计

（一）中国金融资产综合价格指数

金融资产通常包括通货、存款、贷款、非股票证券、保险准备金、股票和其他股权、货币黄金和特别提款权、金融衍生产品和其他应收应付账款。[17]目前中国金融衍生品资产总量和市场规模较小，因此，现阶段只考虑债券、股票、基金三类金融资产。由于房地产税收体系的不完备和近二十年价格的快速上涨，中国的房地产具备很强的投资品属性，房地产价格应该被纳入金融资产价格中。

本文选取中债综合指数、上证综指和中证基金指数分别作为债券价格、股票价格和基金资产价格的基础指数。同时，通过商品房销售总额和商品房销售总面积得到商品房平均销售价格作为房地产价格。所有原始数据均来源于万德数据库和国家统计局，根据数据可得性将研究期设定为2003年第一季度至 2020年第一季度。中债综合指数、上证综指、中证基金指数和商品房平均销售价格的频度均转换为季度数据，所有序列均进行了标准化处理，消除量纲量级的影响。本研究采用主成分分析法合成中国金融资产价格指数，最大程度包含了原有四个价格成分内的信息，同时避免了各合成时各成分权重设定的主观性和僵化，可有效捕捉中国资产价格的整体特征与趋势。

图1为最后合成的中国金融资产价格指数走势图，该指数准确地捕捉到了几乎所有的短期波动：两次中国股票市场的井喷以及全球金融危机后的大跌。同时，也很好地刻画了长期趋势：四万亿的经济扩张计划使中国的资产价格站上了一个新的平台。然后持续的扩张性货币政策推动房地产价格十余年快速增长，目前中国的资产价格已上升到一个前所未有的高位。因此，以它代表中国的金融资产综合价格是具有说服力的。

（二）模型的构建与估计

20世纪90年代末期，时变成分逐渐被纳入了向量自回归模型（VAR）。Cogley & Sargent运用时变参数的向量自回归模型（TVP-VAR）构建了一个包括通货膨胀、失业率和名义短期利率的三变量模型，但假定模型结构冲击的方差不变。[18]Primiceri同时考虑了系数和扰动項方差的时变性，采用带有随机波动率的时变参数的向量自回归模型（TVP-SV-VAR）分析了美国货币政策的传导机制是如何动态变化的，使得研究结论更贴合现实。[19]Baumeister等基于此模型，利用欧洲数据估计了流动性冲击对宏观变量的影响。[20]Nakajima等使用日本经济数据也验证了此模型在宏观经济结构分析中的有效性。[21-23]因此，本文也选择了能有效刻画经济模型的动态结构变化的TVP-SV-VAR模型进行实证研究。

1.TVP-SV-VAR模型的构建

基本的VAR（SVAR）模型定义如下：

Ay t=F 1y t-1+…+F Sy t-s+u t，t=s+1…n，  （13）

式（13）中y t是k个变量构成的向量， A、F 1…F S是系数的k×k矩阵，u t是相应的k个结构冲击向量。假定u t～N（0，∑∑），其中∑=  σ 1 0 … 0

0

0

0 … 0 σ k

遵循常规的递归假设，矩阵A为主对角线均为1的下三角矩阵，且该SVAR模型是可识别的。可以将式（13）改写成以下形式：

y t=B 1y t-1+…+B Sy t-s+A-1∑ε t，ε t～N（0，I k ）  （14）

其中，B i=A-1F i，i=1，2…s。将所有B i中的行元素堆叠，写成一个k2s×1维的向量β，并定义X t=I s（y′ t-1…y′ t-s），其中表示克罗内克乘积。进一步，模型可表示为：

y t=X tβ+A-1∑ε t     （15）

从式（15）可得如下模型：

y t=X tβ t+A-1 t∑ tε t，t=s+1…n，  （16）

式（16）中系数β t、参数A t和∑ t 都是随时间变化的。令 α t表示矩阵A t中下三角元素的堆积向量，h t即为结构冲击的随机波动率， 令h t=（h 1t…h kt）′，其中h jt=lnσ2 jt，j=1…k，t=s+1…n。 因此，在TVP- SV-VAR中，对经济系统的结构冲击的波动性是随时间变化的，而一般VAR假定冲击的方差不变。

假设TVP-SV-VAR模型中的所有时变参数服从一阶随机游走过程，Primiceri指出该假设允许参数暂时或永久性变动，可充分捕捉潜在经济结构的短期和长期变化。即：

β t+1=β t+u βt，α t+1=α t+u at，h t+1=h t+u ht

ε t

u βtu atu ht ～N 0，  1 0 0 0

0 ∑ β  0 0

0 0 ∑ α 0

0 0 0 ∑ h     （17）

其中，t=s+1…n，β s+1～N（μ β 0，∑ β 0），α s+1～N（μ α 0，∑ α 0 ），h s+1～N（μ h 0，∑ h 0）。时变参数β t，α t，h t扰动项无序列自相关，结构冲击ε t也无序列自相关，因此∑ β、∑ α和∑ h都是对角矩阵。

2.变量选取和数据处理说明

本文构建了包括经济周期（ec）、价格型货币政策（r）、资产价格 （fp）和消费者价格指数（cpi） 四个变量的TVP-SV-VAR模型。本研究的重点是货币政策、资产价格和经济波动三者的关系，但稳定物价是货币政策的四大目标之一，而且通货膨胀与资产价格、实体经济之间具有复杂的相互作用，有必要将消费者价格指数 （cpi）作为内生控制变量纳入宏观经济模型中，使得本文的研究逻辑和理论框架更加完整。

我国正处于从数量型货币政策逐步转变为价格型货币政策的改革过程中，而且利率市场化程度有了大幅提高，因此本文主要探讨价格型货币政策（r）与资产价格和经济波动之间的时变影响。鉴于银行间市场的拆借利率是影响市场资金成本和资金供给的重要因素，其变化与货币政策的实施基本同步，所以本文选用7日期同业 拆借加权平均利率作为价格型货币政策（r） 的代理指标[24，25]。本研究基于Christiano &  FitzgeraldBP滤波方法[26]，参考伊楠和张斌[27]、范小云等[28]、毛毅[29]的文献，剔除长期趋势对应的低频成分，把由5 ～16个季度的高频域识别后的实际GDP季度同比增长率作为经济周期 （ec）的代理变量。上一节合成的金融资产综合价格指数作为中国金融资产价格（fp） 的代理指标。

所有变量均经过季节调整剔除了季节影响， 名义同业拆借利率也转化为实际利率。由于7 日期同业拆借加权平均利率是2006年10月才正式发布，所以本研究将数据选取区间确定为2006年第四季度至2020年第一季度，共计54个观测值。

3.参数估计与检验

本研究首先对模型中的所有变量进行了平稳性检验，结果表明四个变量均是零阶平稳。TVP-SV-VAR 模型一般采用基于马尔科夫链蒙特卡罗（MCMC）方法的贝叶斯估计。受限于样本数量，设定模型的滞后期为2，MCMC抽样次数为10000次，利用Oxmetrics6软件以及Nakajima的TVP-SV-VAR软件包进行模型参数估计[30]。

表1为模型时变参数等估计结果。在实证中，不相关样本数量越多，估计结果越好。一般从经验来看，抽样次数足够多，无效因子小于100，则认为模型中产生了较多的不相关样本。表1中无效性因子均小于100，表明模型中所有参数都产生了非常有效的样本。CD统计量反映的是估计的参数是否趋于后验分布，一般认为CD统计量小于1则不能拒绝趋于后验分布的原假设。如表1所示，在5%置信水平下，CD统计量均小于1，表明预烧期能较大程度地使马尔科夫链趋于集中。总的来说，模型的估计效果十分不错，为下一步有效地进行实证结果分析奠定了基础。

四、实证结果分析

（一）变量结构冲击的随机波动特征

图2反映了经济波动、货币政策、资產价格和物价水平四个变量结构冲击的随机波动特征，显示了对结构冲击波动率采取时变假定的必要性。从图2可以看到，经济增长的随机波动率呈现逐渐下行的态势，与目前中国的经济周期具有波幅减小、周期长度增加的趋势吻合。但研究期间仍有个别阶段，如2015年，经济波动幅度较大。从价格型货币政策波动率的时变特征来看，研究期内同业拆借利率的波动率呈平稳下行的态势，且2015年以后波幅逐渐变小，说明了金融市场的逐步完善与稳定。中国金融资产价格的波动率自2012年以后缓慢增长，并在2015年达到最高点，之后开始下降。目前波动率处于较低水平。这表明中国的资产价格虽然日益提高，但其波动主要来自证券市场，2015年的波动率尖峰正对应当时剧烈的股市震荡。最后，消费者价格指数的波动率与资产价格形成了鲜明对比，在整个研究期内基本为常数，而且趋近于零，与近十几年非常平稳的物价水平吻合。

（二）时变脉冲响应分析

TVP-SV-VAR模型的时变效应表现为可以在每一个时点上得到不同的脉冲响应函数和脉冲响应曲线，一般用两种形式进行刻画：一种为等时间间隔的脉冲响应函数，即在研究期每一时点刻画它们对相同时间间隔期以前到来的冲击的脉冲响应值;另一种为特定时点的脉冲响应函数，即刻画对研究期内一个特定时点到来的冲击在后续1，2，3……n个时期的响应值（类似非时变参数VAR的脉冲响应函数）。模型可得到所有内生变量的两两脉冲响应图，本研究重点选择与研究目标密切相关的部分进行深入分析。

1.等时间间隔的脉冲响应函数。

图3（1）描绘了资产价格对不同提前期的单位标准差利率冲击所产生的等时间间隔脉冲响应曲线，实线、长虚线和短虚线分别代表资产价格对3个季度、4个季度以及5个季度以前的利率冲击的响应。这些脉冲响应曲线走势大体一致，说明资产价格对利率变动的反应具有一定的持续性。研究期内资产价格对利率变动的敏感性具有明显的时变效应：在大部分时期，资产价格对利率提高的反应是负向的，即利率的提高会降低金融资产价格。但在2007～2008年和2014～2015年两次股市快速上涨时期，响应函数两次出现了为正的情况，表明在资产价格暴涨期间，采用加息的紧缩性货币政策未必能够起到降低资产价格的作用，甚至进一步推高了资产价格。这一结果与Gali、陈浪南和刘劲松从理论和实证上对美国和中国资本市场得出的结论一致：当存在理性资产价格泡沫时，在均衡状态下，资产价格可能随着利率的提高而上升。

类似地，图3（2）描绘了资产价格对宏观经济冲击的等时间间隔脉冲响应。从图中可以看出：除了2007～2008年次贷危机这一特殊时期，中国的资产价格对于不同提前期的宏观经济冲击的响应几乎均为正向，即经济增长速度越高，资产价格也越高，但2015年以后，经济增长对资产价格的推升作用显著减小。金融资产价格对不同提前期（3，4，5个季度）的宏观经济冲击的响应幅度基本相同。

图4（1）是经济波动对利率冲击的等时间间隔脉冲响应。如图所示，提前期为三四个季度的两条等时间间隔脉冲响应曲线在整个研究期内基本位于零线之下，说明紧缩性货币政策抑制经济增长，而扩张性货币政策能促进经济增长。而提前期为5个季度的等时间间隔脉冲响应曲线在研究期内主要围绕零值上下波动，说明货币政策对宏观经济作用的短期性。同时，宏观经济对利率变动的敏感性也具有明显的时变效应：从2015年开始，宏观经济对利率冲击的响应逐渐减弱， 即利率对宏观经济的负向影响程度在不断减小，“利率下降→宏观经济增长”这一政策传导渠道的有效性降低。其中一个重要原因可能是：2015年以后中国金融资产价格泡沫成分大增，提高利率进一步推动资产价格上升，信贷市场萎缩程度减轻，实体经济受到的负面影响较小。简而言之，“理性资产价格泡沫效应”削弱了“金融加速器效应”。

图4（2）则描绘了经济波动对资产价格冲击的等时间间隔脉冲响应曲线。从中可以看出，3个季度前的正向资产价格冲击能够推动经济增长，4个季度前的资产价格冲击对经济增长已影响不大，5个季度前的资产价格上升反而抑制了经济增长，说明资产价格上涨对经济增长的推动具有一定的短期性。而且宏观经济对资产价格冲击的反应也具有时变性和非对称性：三条脉冲响应曲线在2012年以后有明显的下行趋势。在研究期末宏观经济对提前3个季度的资产价格冲击响应降至零，2014年以后宏观经济对提前4、5季度资产价格冲击响应都变为负值。这表明研究期内资产价格对于宏观经济的拉动作用逐渐减弱，甚至在2014、2015年金融资产价格高企以后，资产价格快速上涨可能会因为从实体经济“抽血”而损害宏观经济。

2.不同特定时点的脉冲响应函数

TVP-SV-VAR模型可以为研究期内每一个时点提供一条常规脉冲响应曲线。本研究选取2009年第1季度、2012年第1季度、2015年第1季度三个时点，进一步分析不同时点下结构性冲击对经济变量的影响，以探寻不同经济、金融环境中价格型货币政策、资产价格和经济波动之间的动态关系。选择这三个时点主要是因为：第一，2009年第1季度中国经济在全球金融危机的影响下遭受重创，处于历史中最大力度的利率调整时期。第二，2012年第1季度是中国经济增速阶段性换挡的起点，选取这一时点可以呈现在经济“新常态”时期这三者之间的新型关系。第三，2015年第一季度以来，中国历经了多次降准和降息，可以考察如此频繁的货币政策调控到底起到了什么作用。另外，从图1的中国金融资产综合价格指数的走势和图2中4个变量的随机波动率可看出，2015年中国金融资产价格攀升到一个前所未有的高位，而实体经济波动则大幅下降。

图5（1）描绘了资产价格在这三个时点对利率冲击的脉冲响应。从图中可以清晰地看到，在2009年第1季度和2012年第1季度，利率冲击对资产价格产生了即期的负向作用，在第2期达到负向峰值后逐渐收敛于零值，而2015年第1季度的脉冲响应曲线却几乎与前两条响应曲线以零轴对称。此图更清晰地验证了图3（1）的结论：在正常经济环境下，资产价格会随着利率的升高而下降;在资产价格高涨期间，采用加息的紧缩性货币政策会进一步推高资产价格。

图5（2）是资产价格在这三个时点对宏观经济冲击的脉冲响应函数。三个时点形成的脉冲响应曲线均在第1期达到正向峰值，而后2009年、2012年第1季度的脉冲响应曲线呈下行的走势，逐渐向零轴附近收敛，说明经济增长有助于金融资产价格上涨。然而，资产价格对2015年第1季度宏观经济冲击的响应程度明显弱于2009年、2012年第1季度，并且其脉冲响应值在第4期后由正转为负，说明在资产泡沫较大的时期，宏观经济对资产价格的正向影响程度较低，而且消失得也较快。

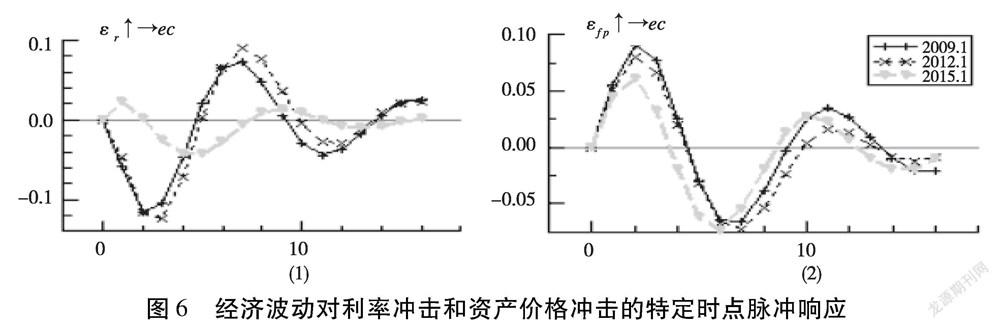
图6（1）是经济波动在这三个时点对利率冲击的脉冲响应函数。2009年和2012年第1季度的脉冲响应曲线基本重合，均在第2个季度达到负向峰值，即利率上升对经济增长的抑制作用在半年后达到最大。在随后的多个季度内，脉冲响应曲线围绕零值波动。但2015年第1季度的脉冲响应曲线却和上述两条脉冲响应曲线很不相同，一直在零值左右小幅波动，这与图4（1）结论一致：在资产价格泡沫时期，宏观经济对利率的反应敏感性也下降了，因为高利率推高了资产价格，降低了“金融加速器效应”引起的信贷收缩程度，减轻了对实体经济产生的负面冲击。

图6（2）描绘的是宏观经济在这三个时点对资产价格冲击的脉冲响应函数。从图中可见，三条特定时点脉冲响应曲线走势极为相似，均在第2个季度达到正向峰值，但响应值在之后的3个季度内逐渐减为负值。另外，2015年第1季度的资产价格冲击对宏观经济的影响最弱。该图更清晰地验证了图4（2）的结论：资产价格上涨能在短期内推动经济增长，但是在长期却会抑制实体经济的发展。当资本市场存在较大程度的资产价格泡沫时，资产价格对宏观经济的提振作用会减小。

另外，在金融资产价格合理和高企的时期，通货膨胀对宏观经济变量冲击响应的非对称性也值得关注。图7（1）（2）描绘了三个时点上消费者价格指数对利率和宏观经济波动的脉冲响应函数。2009年和2012年第1季度两个时点，紧缩性货币政策降低了物价水平，经济增长提高物价水平，符合传统宏观经济学理论的预期。但在金融资产价格高企的2015年第一季度，利率变动对通货膨胀几乎无影响，而经济增长却对降低物价水平有持续性影响，主要原因可能仍是金融市场的投机性货币需求對商品市场的“抽血”效应，是货币政策、价格和经济波动三者的时变关系在商品市场而不是金融市场的反映。因此，传统的货币政策与经济增长、通货膨胀的理论关系也受到挑战，这一点对货币政策在抑制资产价格和物价上涨、促进经济增长的相机抉择中非常重要。

（三）稳健性检验

在前文中，主要讨论的是价格型货币政策（利率）与资产价格、经济波动之间的时变影响关系。虽然数量型货币政策逐步转变为价格型货币政策已是比较明确的改革方向，但我国的货币政策仍处于数量型向价格型转型的过渡阶段，货币供应量对于宏观经济和金融市场的影响依然不可小觑，针对数量型货币政策进行稳健性检验十分必要。因此，沿用上面的模型，将经通胀调整后的货币供给量M2的季度同比增长率作为数量型货币政策的代理指标，取代实际利率来进行稳健性检验。其他三个变量的数据选取以及样本区间与前文保持一致。

检验结果表明：在采用数量型货币政策的模型中，货币政策、资产价格与经济波动之间相互作用的脉冲响应函数没有明显变化，这里重点展示与货币供应量直接相关的特定时点的脉冲响应函数，等时间间隔脉冲响应函数得出的结论与此类似。由于货币供应量与利率升降的方向相反，故乘以-1，以保证其与利率变动方向一致，方便实证结果比较。图8（1）（2）显示了2009年和2012年第1季度紧缩性货币政策将导致资产价格的显著下降和宏观经济的大幅负向波动，而2015年第1季度的脉冲响应曲线与2009年和2012年的走势相反，说明在资产价格高企之时，采用减少货币供应量的紧缩性货币政策也会进一步推高资产价格，而且宏观经济对货币供应量的敏感性也很低，基本在零值附近波动。由于在现实生活中货币供给量和利率的变动并非一致，且二者之间存在时滞，所以资产价格和经济波动对二者的脉冲响应函数图形并不完全一样，但响应的正负结果与基准模型基本一致，表明本文的研究方法和研究结论是稳健的。

五、结论与启示

与过往文献以中国单一资产价格变动为研究对象不同，本文建立包含了股票、房地产、基金和债券在内的金融资产综合价格，进而采用TVP-SV-VAR模型对价格型货币政策、资产价格与经济周期三者之间的影响机制及时变特征进行了较为全面的分析， 并基于数量型货币政策进行了稳健性检验。论文为中国货币政策、资产价格与经济波动之间的作用关系及结构冲击波动率的时变性提供了经验证据，主要得出了如下的研究结论和政策建议：

第一，在正常经济金融环境中，中国存在“金融加速器效应”。但在资产价格已经存在较大泡沫时，“理性资产价格泡沫效应”占主导，资产价格可能会随着利率的提高而上升。采用加息等紧缩性货币政策不仅会严重影响实体经济，还可能进一步推高资产价格。因此，在存在较大资产价格泡沫时，需要谨慎采用“逆风而动”的货币政策规则，建议着重从改变金融资产收益预期入手，甚至实施暂时性行政手段等方法缓释金融泡沫。第二，随着时间推移和资产价格泡沫增加，货币政策对宏观经济的影响程度在不断减小，即“利率下降→宏观经济增长”这一政策传导渠道的有效性降低，这在一定程度上说明了中国现阶段实体经济与虚拟经济之间的二元割裂在逐渐加大。第三，宏观经济对资产价格冲击的响应具有短期性和非对称性：资产价格上涨能在短期内推动经济增长，但是长期作用较弱。尤其当资本市场存在较大程度的价格泡沫时，资产价格对宏观经济的提振作用不仅会减小，甚至会抑制实体经济的发展。第四，通货膨胀对宏观经济变量冲击的响应也具有非对称性。资产价格合理时期，扩张性货币政策和经济增长提高物价水平。资产价格高企时期，利率变动对通货膨胀几乎没有影响，经济增长反而降低物价水平。这可能是货币政策、价格和经济波动三者的时变关系在商品市场而不是金融市场的反映。第五，基于实体经济下行压力的不断增大，而资产价格已到高位的现实，系统性金融风险与经济紧缩风险并存的复杂局面可能会持续一段时间。虽然相对积极的货币政策仍然是重要的宏观调控手段，但可更多采用非常规货币政策，通过有针对性地降低优质企业、小微企业以及特定行业和特定区域的信贷成本等手段取代“大水漫灌”的方式来提振实体经济。另外，应该适当重视财税政策的作用，也许辅助以征收和提高物业税、资本利得税等财政手段对控制资产价格上涨更为有效。 “扩信用，稳货币，重财政”也许是宏观经济调控的一个方向。更进一步，如何将两种价格——物价和金融资产价格内生于宏观经济框架，建立一个包含“金融加速器效应”和“理性资产价格泡沫效应”的统一模型，以推进对宏观经济变量之间一系列的时变和非对称性关系的研究，为货币政策在多目标权衡下的相机抉择提供参考，是我们未来的研究方向。

参考文献：

[1]Mishkin F S.The Channels of Monetary Transmission： Lessons for Monetary Policy[J]. Nber Working Papers，1996.

[2]Bernanke B S， Gertler M. Agency Costs， Net Worth and Business Fluctuations [J].The American Economic Review， 1989， 79（1）： 14～31.

[3]Bernanke B S， Gertler M，Glichrist S. The Financial Accelerator in a Quantitative Bussiness Cycle Framework[J].Hand Book of Macroeconomics，1999，1：1341～1393.

[4]Gertler M， Karadi P. A Model of Unconventional Monetary Policy [J]. Journal of Monetary Economics， 2011， 58 （1）：17～34.

[5]Oliner S D， Rudebusch G D. Is There a Broad Credit Channel for Monetary Policy？ [J]. FRBSF Economic Review， 1996（1）： 3～13.

[6]GertlerM， Gilchrist S. Monetary Policy， Business Cycles， and the Behavior of Small Manufacturing Firms [J]. Quarterly Journal of Economics， 1994 （109）： 309～340.

[7]Kiyotaki N， Moore J. Credit Cycles [J]. Journal of Political Economy， 1997， 105 （2）： 211～248.

[8]Jordi Gali. Monetary Policy and Rational Asset Price Bubbles[J]. American Economic Review，2014，104（3）： 721～752.

[9]Gali J，Gambetti L.The Effects of Monetary Policy on Stock Market Bubbles：Some Evidence[J].American Economic Journal：Macroeconomics，2013，7（1）：233～257.

[10]NisticòS.2005. “Monetary Policy and Stock-Price Dynamics in a DSGE Framework.”LLEE Working Paper No.28. https：//ssrn.com/abstract=886116.

[11]Kannan P， Rabanal P， Scott A M. Macroeconomic Patterns and Monetary Policy in the Run-Up to Ssset Price busts[J]. IMF Working Papers. 2009： 1～39.

[12]陳诗一. 融资成本、房地产价格波动与货币政策传导[J].金融研究，2016（3）： 1～14.

[13]高小红，苏玮. 股价波动、货币政策规则与宏观经济波动——基于多部门 NK-DSGE 模型的研究[J].经济评论，2017（2）：76～99.

[14]陈继勇，袁威，肖卫国. 流动性、资产价格波动的隐含信息和货币政策选择——基于中国股票市场与房地产市场的实证分析[J].经济研究，2013（11）： 43～55.

[15]闫先东，朱迪星. 资本市场泡沫、 经济波动与货币政策反应[J].国际金融研究，2016（10）： 74～88.

[16]陈浪南，刘劲松. 货币政策冲击对股票市场价格泡沫影响的时变分析[J].统计研究，2018（8）： 39～47.

[17]Department S. Monetary and financial statistics manual[M]. IMF， 2000.

[18]Cogley T， Sargent T J. Evolving post World War II U.S. inflation dynamics[J]. NBER Macroeconomics Annual， 2001， 16：331～73.

[19]Primiceri G E. Time varying structural vector autoregressions and monetary policy[J]. The Review of Economic Studies， 2005， 72（3）： 821～852.

[20]Baumeister C， DurinckE， Peersman G . Liquidity， inflation and asset prices in a time-varying framework for the Euro area. 2008，Manuscript.

[21]Nakajima J，KasuyaM， Watanabe T. Bayesian analysis of time-varying parameter vector autoregressive model for the Japanese economy and monetary policy. IMES Discussion Paper， 2009-E-13， Bank of Japan.

[22]NakajimaJ， ShiratsukaS， Teranishi Y. The e？ects of monetary policy commitment： Evidence from time-varying parameter VAR analysis. IMES Discussion Paper， 2010-E-6， Bank of Japan.

[23]Nakajima J. Monetary policy transmission under zero interest rates： An extended time-varying parameter vector autoregression approach. IMES Discussion Paper， 2011-E-8， Bank of Japan.

[24]饶品贵，姜国华. 货币政策对银行信贷与商业信用互动关系影响研究[J]. 经济研究， 2013， 48（1）：68～82;150.

[25]刘金全，张小宇. 中央银行规避经济收缩和通胀偏好的模式与途径研究[J]. 经济研究，2015，50（12）：29～40;53.

[26]Christiano L， Fitzgerald T. The Band Pass Filter[J].International Economic Review，2003，44（2） ： 435～465.

[27]伊楠， 张斌. 度量中国的金融周期[J]. 国际金融研究， 2016（6）：13～23.

[28]范小云，袁梦怡，肖立晟. 理解中国的金融周期：理论、测算与分析[J]. 国际金融研究，2017（1）：8～38.

[29]毛毅.金融业与实体经济行业间工资差距对中国经济增长的影响研究[J].财贸研究，2020（12）：49～60.

[30]Nakajima J. Time-varying parameter VAR model with stochastic volatility： An overview of methodology and empirical applications[R]. Institute for Monetary and Economic Studies， 2011.

“Financial Accelerator Effect” or “Rational Asset Price Bubble Effect”

- Research on Time-varying Relationship based on Monetary Policy， Asset Prices and Economic Fluctuation

ZHANG Rui，GUO Xiaoman，SHEN Chengcheng

（School of Economics， Sichuan University， Chengdu， Sichuan 610065， China）

Abstract：

Chinas economy is facing downward pressure， and asset prices have reached high level at the current stage. It is very necessary and urgent toexplore how monetary policies balance “steady growth” and “risk prevention” in different financial and economic environments. However， the theory of “Financial Accelerator” and “Rational Asset Price Bubble” provide contradictory theoretical basis for the choice of monetary policies. In this paper， principal component analysis method is adopted to construct comprehensive price indexes of Chinese financial assets including stocks， real estate， bonds and funds. By taking the fourth quarter of 2006 to the first quarter of 2020 as the research period，the time-varying relationship among monetary policy， asset prices and economic fluctuation is studied based on TVP-SV-VAR model. This paper provides empirical evidence for the interaction relationship among the above three and the time-varying characteristics of structural shock volatility. The conclusions are as follows： In the general economic environment， China has a “financial accelerator effect”， but after asset prices reach a high level， the “rational asset price bubble effect” appears， which means， asset prices will rise as interest rate rises;As time goes by and Chinas asset price bubble has increased，the effectiveness of the policy transmission channel of “decline in interest rate → growth of macro-economy” is gradually decreasing;In the short run， rise of asset price drives economic growth while severe bubble may dampen growth;The current impliedmacro-control direction is “expanding credit， stabilizing monetary policy and slack fiscal policy”.

Key words ：

monetary policy;asset price;economic fluctuation;TVP-SV-VAR;time-varying effect

責任编辑：萧敏娜