基于Adam注意力机制的PM2.5浓度预测方法

张怡文,袁宏武,孙鑫,吴海龙,董云春

(安徽新华学院信息工程学院,安徽 合肥 230088)

0 引 言

随着环境污染的加剧、雾霾天气在我国大部分城市的不断蔓延以及大气细颗粒物(PM2.5)对人类健康的影响日益增大[1,2],PM2.5对空气质量的影响已成为政府、环境保护部门以及人们关注的热点问题。

近年来,研究人员对PM2.5浓度的预测进行了大量研究[3],主要采用两大类预测方法。一类是基于线性计算的方法,如基于基因表达式、Logistic回归模型、LASSO回归模型等[4−6],此类方法可以根据数据间的关联性,预测PM2.5浓度;另一类主要采用非线性的计算方法,其中代表性的方法是采用神经网络模型进行预测。很多大气污染物及气象因素与PM2.5浓度之间的关系呈非线性特征[7,8],而神经网络具有较好的泛化能力,能够较好地模拟大气污染物及气象因素的变化过程,因此目前基于神经网络模型的模拟预测方法[9,10]有较大的进展。

随着深度学习在图像处理、语音识别、自然语言处理等领域的广泛应用,少数研究人员开始采用深度学习对天气或雾霾进行预测,如文献[11]选择深度信念网络,认为PM2.5浓度与多种气象因素等有复杂的特征关系,采用大气气溶胶光学厚度和气象参数预测PM2.5浓度值,与神经网络相比,提高了预测准确率。文献[12]认为PM2.5浓度的预测具有时序性,建立了基于时间序列的递归神经网络(Recurrent neural network,RNN)预测模型,并采用长短记忆神经网络[13,14](LSTM)对RNN进行优化,相比神经网络的推荐方法,该方法提高了预测精度。但总的来说,深度学习在PM2.5浓度预测上的应用还处于初期研究阶段。

受上述工作启发,本文采用一种基于时间序列的深度学习模型对大气PM2.5浓度进行预测。考虑到RNN和LSTM对每个时间点上的输入对PM2.5浓度的预测值产生的影响权重均等,从而影响了预测准确性。故提出一种基于Adam注意力机制的PM2.5浓度预测方法,采用注意力机制为时间序列数据分配权重,并利用自适应矩估计[15](Adaptive moment estimation,Adam)算法对RNN和LSTM模型的参数进行寻优计算,找最优参数。实验结果表明,该方法有效地提高了预测准确率。

1 相关工作

1.1 基于时间序列的深度学习模型

传统的数据挖掘方法对污染物及气象因素的特征学习能力较弱,同时对如PM2.5浓度这种具有时间序列特征污染物的历史数据感知能力较差。而深度学习采用的是数据层次化的抽象表达,对PM2.5浓度数据可以以时间块进行层次的划分,故选择RNN之类的基于时间序列的深度学习方法[16],可以对复杂的污染物及气象数据进行深度挖掘,建立基于时间序列的预测方法。

RNN的预测模型如图1所示,每个时刻结点的数据都由当前时刻的输入数据和上一时刻结点的数据构成,输入、输出的每条边上都有权重,分别为W、U、V。RNN网络主要包含两个重要过程,数据的前向传播和后向传播,通过前向和后向传播调整主要参数,使得网络达到最优。

图1 RNN模型Fig.1 Model of RNN

LSTM方法可以解决长时间序列中数据弥散的问题。LSTM在RNN的基础上加入输入门(Input gate)、输出门(Output gate)和遗忘门(Forget gate),让模型有选择的记忆重要数据和遗忘不重要的数据,对RNN的预测方法进行进一步优化。LSTM的结构如图2所示。

图2 LSTM模型Fig.2 Model of LSTM

1.2 注意力模型

神经网络是一种模拟人类大脑的模型,是一种资源分配模型,在某个时刻人的注意力主要集中在某一个或几个焦点;而RNN和LSTM模型对不同的状态时刻数据采用相同的权重进行计算,不符合类脑模型的设计。将注意力机制引入神经网络,将不同时刻的注意力分布不同的权重,这样可以更好地表现不同状态时刻对输出的影响。目前的注意力模型主要基于Encoder-Decoder模型[17]。Encoder用来对输入进行编码,并产生中间编码Ci,在非注意力模型中共享同一个Ci的编码。在注意力模型中,对不同的输入分配不同的Ci编码。Decoder用来进行解码,将中间编码Ci与Y1,…,Yt−1时刻的历史信息一起生成目标输出Yt。基于注意力的Encoder-Decoder模型(A-ENDE)如图3所示。

图3 A-ENDE模型Fig.3 Model of A-ENDE

其中Yt的计算公式为

式中:Yt为t时刻的预测输出;f函数为Decoder过程选择的变换方法,如CNN、RNN、LSTM等。Ci的计算公式为

式中:Lx是输入序列xi的长度;hj为第 j个输入的中间隐状态值;aij为第i个输出时,第 j个输入的注意力概率分配,主要表示输出Y与输入x之间的对齐概率。aij的计算在不同的数据集和模型中对应不同的方法。

1.3 Adam优化器

Adam[18,19]是一种基于一阶梯度的随机目标函数优化算法,用来更新和计算模型训练和模型输出的网络参数,使模型逼近或达到最优,从而得到最小化(或最大化)损失函数LHuber,以梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam算法的优点在于经过偏置校正后,每一次迭代学习率都有确定范围,使参数比较平稳。网络参数更新过程为

式中:mt和vt分别为一阶动量项和二阶动量项;β1,β2为动力值,默认值为0.9和0.999。mt和vt的偏差修正分别为,其计算公式分别为

那么t+1时刻即第t+1次迭代模型的参数θt+1为

式中:θt表示t时刻即第t次迭代模型的参数;η为超参数,默认为10−5;ε是一个取值很小的数(该实验中取为10−8),其作用是为了避免分母为0。第t次迭代代价函数关于θt的梯度gt计算公式为

损失函数LHuber利用的是Huber损失的计算方法,其计算公式为

式中:Y为预测值,f(x)为真实值,当LHuber最小时即可得到模型达到最优时的迭代次数和训练次数。

2 基于Adam注意力模型的PM2.5浓度预测

由于PM2.5浓度具有较强的时间序列特征,实验分别选择RNN和LSTM为Encoder和Decoder阶段的变换方法,基于注意力的PM2.5浓度预测模型如图4所示。

图4所示的模型中,采用RNN进行Encoder-Decoder的预测方法记为ARNN,采用LSTM进行Encoder-Decoder的预测方法记为ALSTM。其中注意力部分的计算以及基于Adam算法的最优参数都在Encoder阶段,计算公式为

式中:pmi表示第i个时刻的PM2.5浓度的输入值;pˆmi表示第i个时刻的Encoder后的预测输出。aij表示Encoder编码后的输出与真实值之间的对齐概率分布,由式(10)可以看出,偏差越小,权重分配越大,也就是对输出的影响程度越高。

根据图4的注意力模型进行PM2.5浓度预测的步骤如下:

1)选择Adam算法,训练RNN和LSTM中的参数学习率α、迭代次数e进行寻优,计算参数最优组合;

2)将具有时间序列特征的原始数据pmi=[pm1,pm2,···,pmt]做为输入,将1)中的最优参数代入RNN和LSTM作为Encoder编码方法,输出中间隐状态序列hj=[h1,h2,···,ht]和Encoder阶段的预测输出序列

3)将原始输入pmi和2)中输出的序列,根据公式(10)计算每个输入时刻的权重aij,并通过softmax进行归一化;

4)将3)中得到的aij和2)中的中间隐状态hj,代入式(2)得到中间编码Ci;

5)将4)中得到的Ci与原始输入pmi做为输入,根据式(1)选择RNN和LSTM为Decoder解码方法,解码输出 PM2.5浓度的预测值 PMi=[PM1,PM2,···,PMt]。

3 实验设计及结果分析

3.1 数据采集和预处理

实验采集了合肥市10个观测点PM2.5浓度的历史数据,数据周期从2016年1月1日–2018年12月31日,污染物数据来自www.pm25.com[20]。

由于数据采集时有时间数据丢失,此时根据式(11)进行数据补缺,

式中:Di为缺失的PM2.5浓度小时数据,Di−1为缺失数据最近的上一时刻PM2.5浓度数据,Di+1为缺失数据最近的下一时刻PM2.5浓度数据。

3.2 评价标准

实验采用均方根误差(Root mean squard error,RMSE)做为评价标准[21],其表达式为

式中:Xobs,i表示第i个预测值,Xmodel,i表示第i个真实值,n表示预测次数。ERMS的值越小表示预测误差越小,因此ERMS越小越好。

3.3 实验结果及分析

实验分两组进行,第一组为利用历史PM2.5浓度预测未来PM2.5浓度值;第二组为利用历史PM10、CO、CO2、SO2、O3等相关污染物浓度数据预测未来PM2.5浓度值。两组实验均选择2016–2018年每年前11个月数据作为训练集,12月份的数据作为测试集进行实验。实验选择BP、RNN、LSTM与本文提出的AT-RNN和AT-LSTM五种算法,采用ERMS指标进行算法的衡量标准。每年实验重复5次,取均值对实验结果统计分析。

五种算法均采用Adam算法对参数学习率α、迭代次数e进行训练。p在10～50之间,根据经验值,选择p值为35。根据Adam算法的LHuber值,α为0.6−x,x取值在−5～0范围内,e在1～10000范围内进行训练,选取LHuber值最小的α和e为模型的最佳参数。

第一组实验采用2016–2018三年的PM2.5浓度数据进行单指标预测,用Adam算法分别训练α、e两个参数,训练过程如图5和图6所示。

图5 参数α训练Fig.5 Training of parameter α

图6 参数e训练Fig.6 Training of parameter e

由图5、图6可以看出,α取值在0.006时LHuber最低,故实验中,α取值为0.006;2016–2018三年α最低的e的取值分别为:1076、697、2547,故以此训练结果为e的参数进行实验。

第二组实验采用2016–2018三年的PM10、CO、CO2、SO2、O3等多指标相关污染物浓度数据预测PM2.5浓度值,用Adam算法分别训练α、e两个参数,训练过程如图7和图8所示。

图7 参数α训练Fig.7 Training of parameter α

图8 参数e训练Fig.8 Training of parameter e

由图7、图8可知,α取值在0.006时LHuber最低,故实验中,α取值为0.006;2016–2018三年LHuber最低的e的取值分别为:4729、1919、408,故以此训练结果为e参数进行实验。

接下来,实验分单指标预测和多指标预测两组进行,每组实验训练集均为每年前11个月的历史数据,测试集为每年12月份的数据。第一组单指标预测实验结果如图9所示,可以看出,BP算法预测的ERMS最大,RNN、LSTM模型比BP预测模型的ERMS低,加入基于Adam注意力模型的AT-RNN和AT-LSTM分别比RNN、LSTM预测模型的ERMS更低。但单指标预测的ERMS值都在40以上,整体偏高。

第二组多指标预测实验结果如图10所示,可以看出,BP算法预测的ERMS最大,RNN、LSTM模型比BP预测模型的ERMS低,加入基于Adam注意力模型的AT-RNN和AT-LSTM分别比RNN、LSTM预测模型的ERMS更低。同时多指标预测的ERMS值均在30以下,比单指标预测ERMS降低了10以上,有较大提升,说明相关污染物对PM2.5浓度影响较大。

由图9和图10可以看出,基于Adam注意力的模型可以进一步改善RNN、LSTM结构,说明:1)不同时间的历史PM2.5浓度值对未来的PM2.5浓度预测值的影响力不同;2)Adam模型可以帮助注意力模型寻找最优参数组合,降低预测误差。

图9 单指标ERMS对比Fig.9 Comparison of ERMSof single indicator

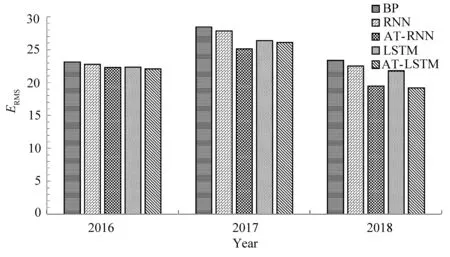
图10 多指标ERMS对比Fig.10 Comparison of ERMSof multiple indicators

4 结 论

提出了一种基于Adam注意力机制的PM2.5浓度预测方法,注意力机制对基于时间序列的PM2.5浓度数据进行注意力权重分配,选择Adam算法对编码阶段的RNN和LSTM的参数进行最优选择,并将RNN和LSTM做为该模型的Encoder和Decoder部分的编码、解码方法对PM2.5浓度进行预测。通过实验证明:基于时间序列的PM2.5浓度数据适合采用RNN和LSTM方法进行注意力模型建模;同时加入基于Adam注意力机制的AT-RNN和AT-LSTM模型,可以提高预测的准确率。

基于Adam的注意力机制提高了PM2.5浓度预测的准确率,但通过数据分析发现,由于数据量较少,依然会影响预测结果,如在两组实验中2017年的预测误差都偏大,通过数据排查发现2017年数据缺失较多,故影响预测结果;同时PM2.5浓度成因复杂,两组实验采用PM2.5浓度的历史数据对未来的PM2.5浓度值进行预测,以及通过PM10、SO2、CO2、CO、O3等污染物对PM2.5浓度进行预测,都没考虑到气象因素对PM2.5浓度的影响。下一步将继续采集数据,并加入气象数据对PM2.5浓度进行预测,进一步提高预测准确率。