基于机器视觉轮廓提取的平滑处理算法*

李建鑫 ，陈 鸿 ，王晋祺

(1.中北大学 仪器与电子学院，山西 太原 030051；2.上海无线电设备研究所，上海 201109)

0 引言

近年来，基于机器视觉的眼镜镜片轮廓提取系统因为其优良的效率与成本而被市场快速推广[1]。然而在利用机器视觉提取镜片轮廓过程中，会有难以避免的环境干扰光造成误差，严重影响提取的镜片轮廓数据的光顺与精度。

B 样条曲线拟合的定义一般是指：给定一组已知的数据点，要求寻找一条B 样条曲线逼近或通过这些数据点[2]。对B 样条曲线拟合问题的研究在高精加工领域有着非常重要的地位，有诸多学者取得了大量卓有成效的成果[3-4]。目前最小二乘法使用最普遍的B 样条曲线拟合方法，目标是极小化各个数据点与所拟合的B 样条曲线上的对应点的距离平方和[2]。然而由环境干扰光造成的误差总是集中分布，且偏差的方向总是向内，不适合使用最小二乘法进行拟合。

本文针对环境干扰光造成的镜片轮廓上的误差进行了特征分析，并结合镜片轮廓为凸曲线的特征，给出了专门适用的基于三次B 样条曲线拟合的方法：首先依据一定的特征剔除受环境干扰光影响产生误差的轮廓段；然后使用基于三次B 样条曲线的保形插值算法对被剔除的轮廓部分进行插补。最后通过实验实现了对该算法提高数据精度效果的量化分析，验证了该算法对环境干扰光造成的误差有着显著的修复效果。

1 环境干扰光造成的误差特征分析

基于机器视觉的眼镜镜片轮廓提取系统可简化为图1 所示的投影模型，A 面是一个平行光源，B 是待提取轮廓的物体，C 面是感光器件。当平行光由A 面射向C 面时，待提取轮廓的物体B 对平行光进行遮挡，在C面产生待提取物体的投影B′，由感光器件C 对投影B′进行测量以提取轮廓[5]。然而环境中存在不可避免的干扰光，如在图1 中由D 点发出的光，会在B 的投影的轮廓上生成一个光斑D′。

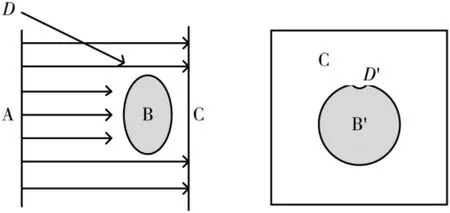
图1 轮廓提取系统模型图

系统提取到的轮廓由有序的离散坐标点组成，现实中的眼镜镜片轮廓线为凸曲线，因此理想中提取到的轮廓应为由n 个顶点构成的凸n 边形。图2 所示为利用机器视觉提取的眼镜镜片轮廓图，在轮廓上取一个区域I，图3 为图2 中此区域的放大图。

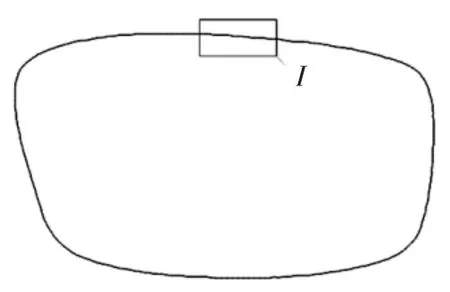
图2 眼镜镜片轮廓图

图3 I 区域局部放大图

在图3 中可以明显观察出提取到的轮廓上有许多凹陷的部分，这正是因为如图1 中的光斑D′的影响。将轮廓上凹陷的顶点称为轮廓的凹点，并把凹点作为环境干扰光所造成的误差的特征体现。

2 凹点的定义与检测方法

根据上述在几何上这样定义眼镜镜片轮廓上的凹点：在眼镜镜片的多边形轮廓上取一个顶点B，在顶点B的顺时针方向取任意的顶点A、在顶点B 的逆时针方向取任意的顶点C，当满足时，如果存在这样的顶点A、顶点C，使在的顺时针方向，则顶点B 为此多边形轮廓的凹点。

对凹点的检测程序流程图如图4 所示。

遍历轮廓上所有顶点后，找到轮廓上的所有凹点。这些凹点不仅本身就是误差，而且在后续的磨削加工中，这些凹点还会造成对其他顶点的过切，进一步恶化眼镜镜片轮廓的精度。因此本文采用首先剔除轮廓上检测出来的所有凹点，然后再对剔除凹点的部分进行插补的方案。剔除所有凹点后的轮廓顶点图如图5 所示。

3 基于B 样条曲线的保形插值方法

3.1 B 样条曲线的数学表达式

一条k 次B 样条曲线可以用一条分段的有理多项式矢函数来表达[6-7]，其表达的公式为：

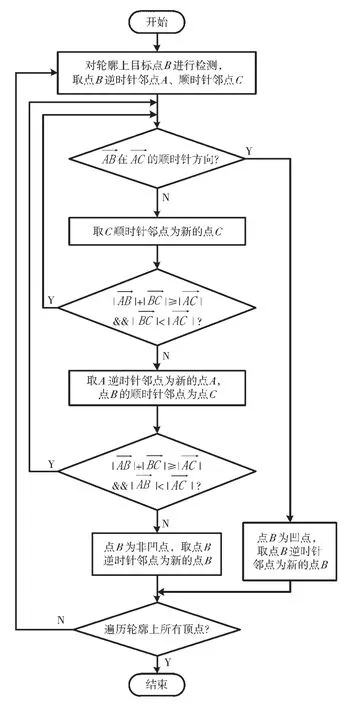
图4 凹点检测流程图

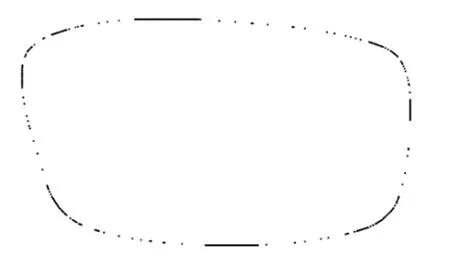
图5 剔除凹点后的轮廓图

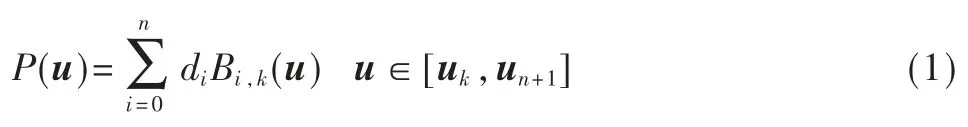
式中，di(i=0，1，2，…，n)为构造B 样条曲线的n+1 个控制顶点；Bi，k(u) 表示的是k 次规范的B 样条基函数，由节点矢量u=[u0，u1，u2，…，ui+k+1]根据de Boor-Cox 递推公式定义：

3.2 B 样条曲线的保形插值方法

众所周知B 样条曲线不具有插值性，待B 样条曲线插值通过的点被称为型值点，构造插值B 样条曲线需要先用型值点求出控制点，然后再用控制点生成B 样条曲线[8]。

常用的求控制点的方法有反算法[9]和迭代算法[10]。然而这两种算法运算量较大，并且用这两种算法求出的控制点所构造的B 样条曲线无法保证具有和型值点多边形相同的凹凸性。目前有针对基于权因子的NURBS保形插值曲线的研究[11]，然而权因子的确定较为复杂，运算量较大。综合考虑该算法的使用场景，本文采用株洲工学院方逵教授提出的保形B 样条插值算法[12]并针对适用场景进行了改进。

定理1：如果相邻的3 个控制点dk、dk+1、dk+2共线，且dk+1=(dk+dk+2)/2，则三次均匀B 样条曲线插值控制点dk+1[12-13]。

根据定理1，按如下过程求得控制点：设需要插值的型值点为Vi(i=0，1，2，…，n)，型值点构成的多边形轮廓为(V0，V1，V2，…，Vn)，如图6 所示。

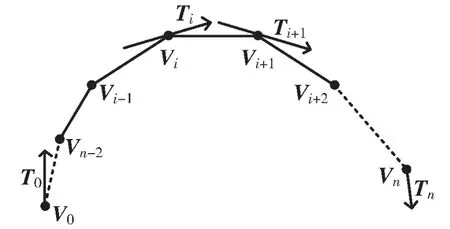
图6 型值点多边形

定义三次B 样条插值曲线P(u)的端点切矢量为给定值T0、Tn。在内部型值点Vi处的切矢量Ti为：

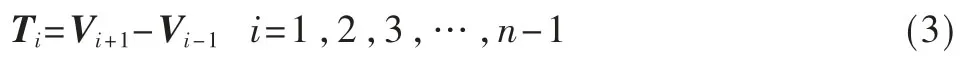
则三次B 样条插值曲线的控制点定义为：

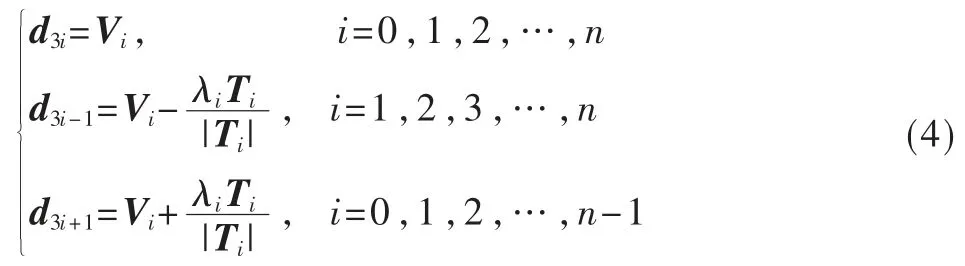
其中，λi是可调节参数。根据定理1，以di(i=0，1，2，…，3n)为控制顶点的准均匀三次B 样条曲线插值所有的型值点Vi(i=0，1，2，…，n)。

已知眼镜镜片轮廓线是凸曲线，因此需要保证生成的插值三次B 样条曲线也是凸的，根据B 样条曲线的保凸的特性，当控制多边形(d0，d1，d2，…，d3n)为凸多边形时，即可保证由此控制多边形生成的B 样条曲线为凸曲线。本文给出要使控制多边形(d0，d1，d2，…，d3n)为凸多边形对λi的要求。

如图7 所示，由型值点Vi-2、Vi-1构造矢量由型值点Vi+1、Vi+2构造矢量。型值点Vi的切矢Ti所在的直线与所在的直线交于点Ri0，型值点Vi的切矢Ti所在的直线与所在的直线交于点Ri1。其中i=1 时将端点V0处的切矢量T0作为；i=n-1 时将端点Vn处的切矢量Tn作为不存在点Ri0；i=n 不存在点Ri1。

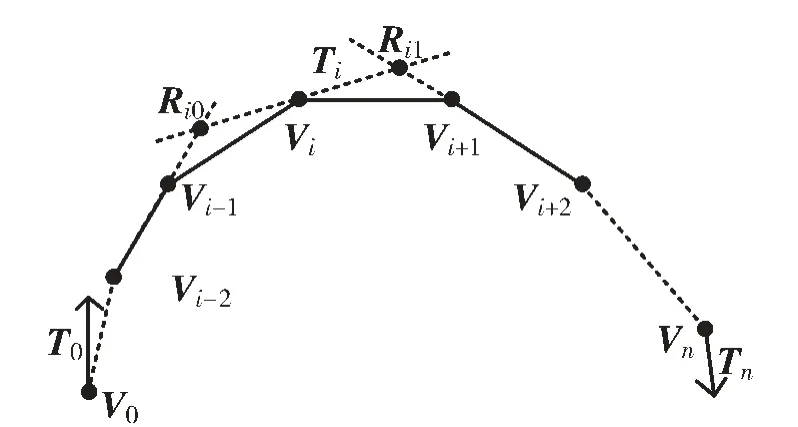
图7 保形条件说明

为了使插值曲线保凸，即以di(i=0，1，2，…，3n)为顶点的控制多边形(d0，d1，d2，…，d3n)为凸多边形，λi需要满足条件：

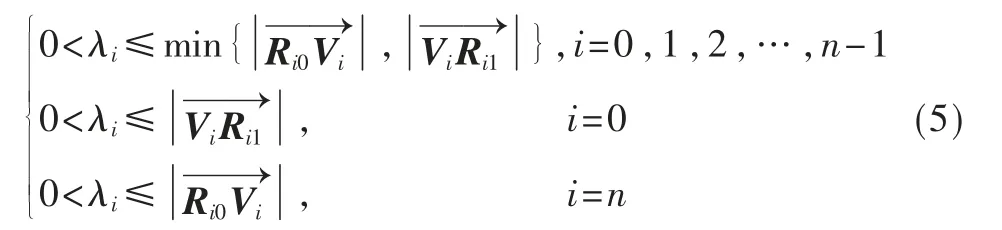
下面给出保凸插值的程序框图，如图8 所示。

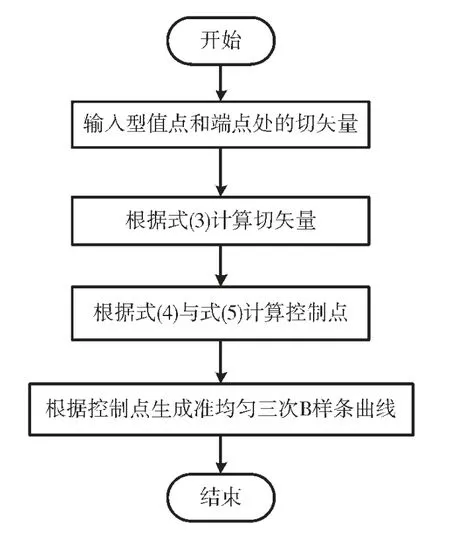
图8 保形插值的程序框图

3.3 眼镜镜片轮廓的保形插值

虽然图5 所示轮廓的顶点中已经不存在凹点，但是相邻顶点之间的间隔很不均匀，有的间隔过大，严重损失精度，且无法进行后续的磨削加工。为此，本文基于上述的B 样条曲线对去除凹点后的轮廓部分进行插补处理。

图5 显示去除凹点后的轮廓总是被去除大量连续的顶点，这是因为轮廓上的凹点数量比较多，且总是集中出现。把这样凹点连续出现的轮廓段称为凹点段。如果两段凹点段之间的间隔只有一个顶点，就把这两个凹点段作为同一段来处理。将轮廓上的局部放大图图3 所显示的轮廓上的凹点进标记，结果如图9 所示，在图9中凹点段(B，…，C)、凹点段(C，…，D)、凹点段(D，…，E)作为同一凹点段(B，…，E)进行处理。

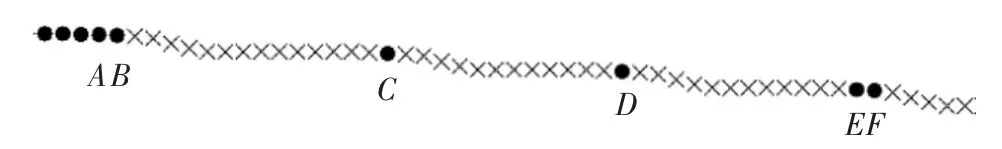
图9 凹点段示意图

对凹点段(B，…，E)的保凸插值：将点B、点C、点D、点E 作为型值点，将作为端点切矢量，按照图8所示流程生成插值曲线。结果如图10 所示。

图10 凹点段插补示意图

对图5 中的整个轮廓去除凹点部分进行保凸插值并对插值曲线进行等步长离散化，结果如图11 所示，在轮廓上消除了所有凹陷的部分，且因为由三次B 样条曲线进行插补，所以光顺度较好，对环境干扰光造成的误差有明显的修复效果。

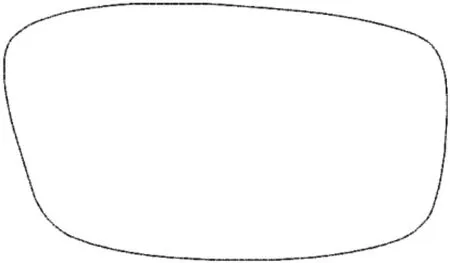
图11 修复误差后的轮廓图

4 设计实验定量分析算法的效果

现实中的眼镜镜片轮廓线通常都是比较复杂的曲线，难以得知其准确的轮廓数据，不便于对本文提出的平滑处理算法提高数据精度的有效性进行量化分析。为此本文设计了以下的实验：

(1)使用基于机器视觉的眼镜镜片轮廓提取系统提取标准圆形镜片的轮廓，提取到的轮廓如图12 所示。

(2)用本文提出的平滑处理拟合算法对环境干扰光造成的误差进行修复处理，效果图如图13 所示。

图12 提取到的圆的轮廓图

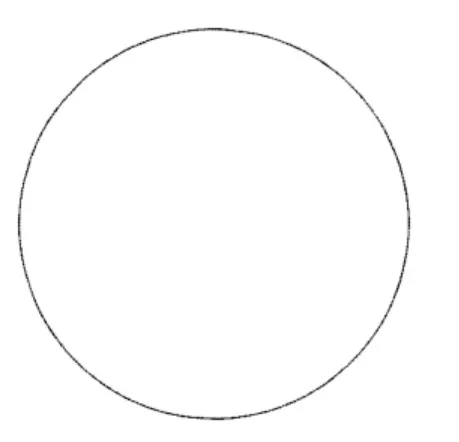
图13 修复误差后的圆的轮廓图

(3)分别将平滑处理前和平滑处理后的轮廓数据用最小二乘法拟合圆，最小二乘法是一种最常见的数学优化方法，通过最小化误差的平方和找到与所提取到的轮廓数据最吻合的圆的参数方程[14]。

设最小二乘圆的参数方程为：

式中，(xc，yc)表示的是拟合出来的圆心坐标，R 表示的是拟合出来的圆的半径。最小化误差的平方和建立的模型为：

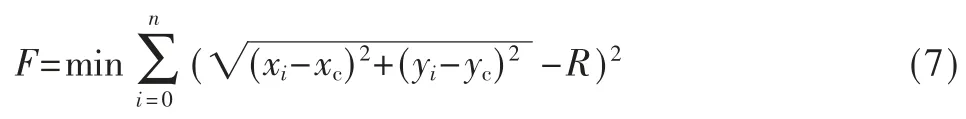
式中，(xi，yi)表示的是提取的轮廓上的离散坐标点。对该模型的求解属于非线性最小二乘法问题[15]，计算复杂，运算量较大。本文先将非线性最小二乘问题转换为线性问题[16-17]，方法如下。令误差项变为：

为对此模型求解，参考文献[16]、[17]，设中间变量：

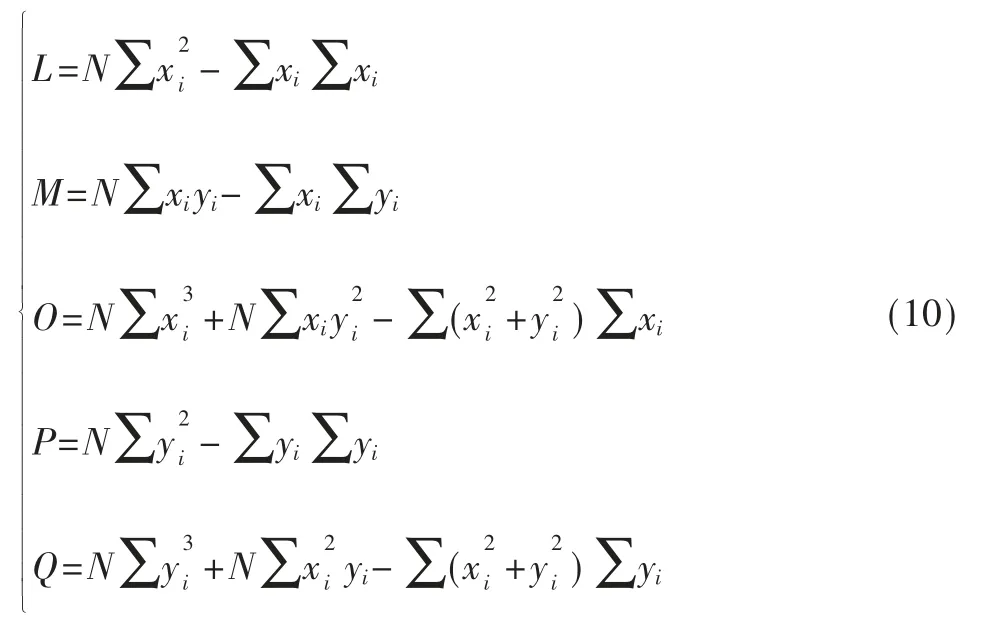
式中，N 表示总点数。模型式(9)的解为：

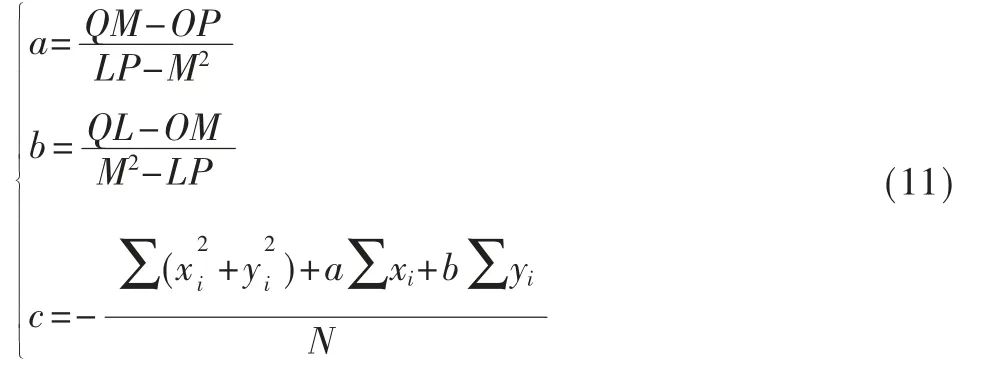
根据式(11)，最小二乘拟合圆的圆心(xc，yc)和半径R的估计值为：

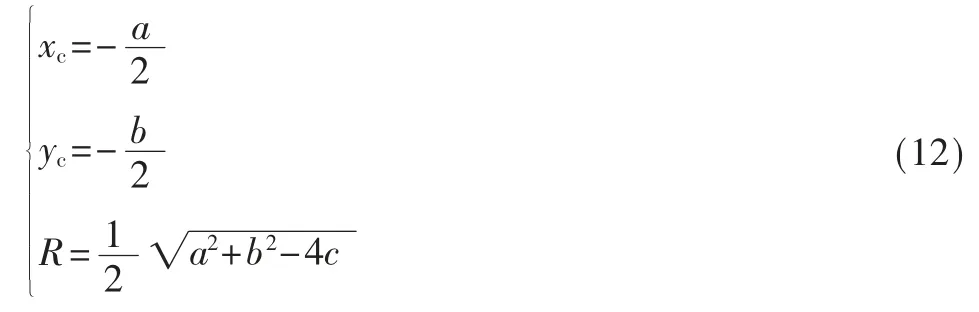
由最小二乘法拟合圆的参数和轮廓数据(xi，yi)求得轮廓数据的最小二乘拟合过程中的均方差为：

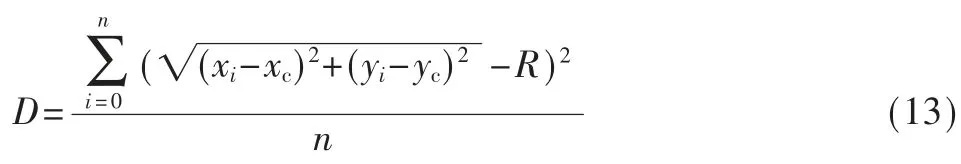
最小二乘法拟合的圆的圆度误差δ 为：

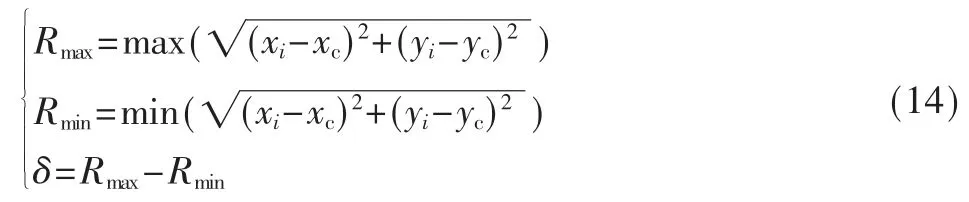
本文的目的是对提出的平滑处理算法的效果进行量化分析，因此分别将平滑处理前和平滑处理后的轮廓数据用最小二乘法拟合圆的均方差与圆度误差进行比较。均方差与圆度误差越小，说明轮廓数据与圆的吻合程度越高，此轮廓的精确程度要更好[18]。在不同的环境光下多次实验，结果如表1 所示。

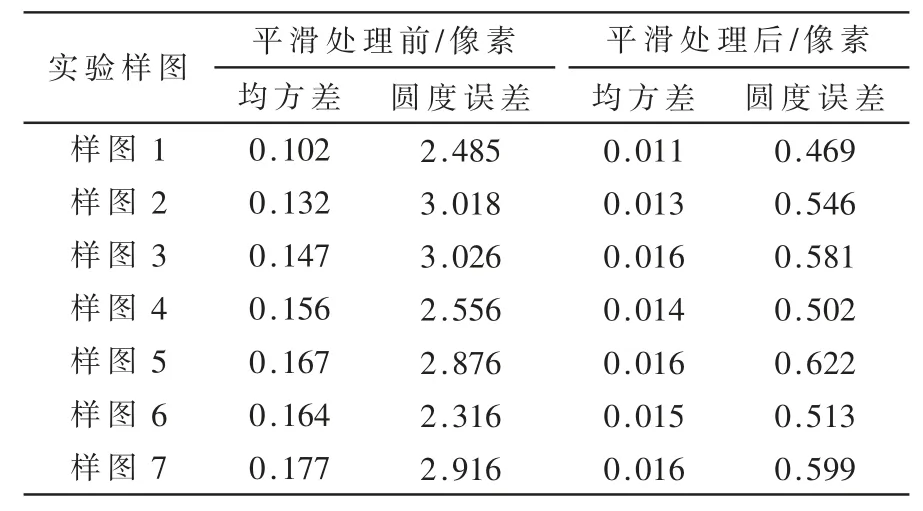
表1 修复误差前后的轮廓数据拟合圆的对比

从表1 可以看出，在使用本文的平滑处理算法对轮廓数据进行处理后，最小二乘法拟合圆的均方差减少了80%～90%，圆度误差减少了70%～80%，轮廓与标准圆的吻合程度显著提高，轮廓数据的精度显著增加。证明本文提出的平滑处理拟合算法对基于机器视觉的眼镜镜片轮廓提取系统有着良好的平滑去噪与误差修复效果，大幅度提高了系统提取的轮廓的光顺与精度。

5 结论

针对使用机器视觉提取轮廓过程中环境干扰光造成的误差，本文通过分析误差的特征，提出了一种全新的平滑拟合算法，并设计实验验证了该算法可以显著提高基于机器视觉的眼镜镜片轮廓提取系统的光顺与精度，且该算法运算高效、编程简单。该算法的应用场景存在一定的限制，适用于轮廓是凸曲线的场景，但是对于轮廓上有较少拐点的情况，该算法也有一定的指导启发意义，可以通过对轮廓进行变形、分段等操作，构造出凸曲线，以适用该算法。