具有拓扑切换特性的离散型不确定时空网络的指数同步

韩昌辉 葛连珺 高丽宇 吕 翎

自然界存在着大量的复杂动态网络，并且复杂动态网络在物理学、神经学、信息通信以及保密技术等领域中均有着重要应用.其中，作为复杂动态网络的一种关键性集体行为，其同步化现象的研究也越来越受到国内外学者的广泛关注[1-5].长期以来，基于稳定结构的网络同步研究一直是人们研究的主要方向[6-9].然而，实际网络的拓扑结构常常是变化的.其原因在于在实际应用中，网络节点的连接方式经常由于连接故障或新节点的加入而改变，进而使得网络的拓扑结构随之改变，从而使网络同步的实现变得更加困难，增加了网络同步状态发生崩溃的可能性.因此，具有拓扑切换特性的网络同步研究也就成为了目前人们研究的热点问题.

目前，具有拓扑切换特性的复杂网络的同步研究已有文献报道.其中典型的如Zhai[10]研究了具有拓扑切换特性的非线性系统构成的网络的同步行为.文献[11]研究了具有切换有向拓扑的多智能网络的一致性跟踪控制问题.文献[12]中，Fan 等研究了具有切换拓扑特性的异构复杂网络的准同步行为.文献[13]报道了具有Markovian 切换特性的耦合神经网络的自适应指数同步问题.这些工作为我们进一步深入地研究具有拓扑切换特性的网络同步问题奠定了理论基础.

然而，已报道的上述成果中其同步技术仍具有若干局限性.例如文献[13]中的拓扑结构切换利用的是Markovian 切换，人们很难对其进行控制.而在实际中，常常需要根据人们的实际需求随时进行网络拓扑结构的切换.同时，网络中参数的未知性也是实际网络受到外界干扰而具有的不稳定因素.不难看出，含有未知参数的网络同步研究十分必要.另外，有关连续型网络同步研究的文献也比较多见，而离散型网络的同步研究相对较少.其中较为典型的工作如Zhang 等[14]利用线性矩阵不等式技术研究了具有时变时滞和随机扰动的离散时间网络的指数同步问题.文献[15]研究了一类具有不确定内耦合的离散时间随机网络的同步和状态估计.Cheng等[16]研究了具有时延耦合的离散动态网络的牵制同步，并依据牵制控制技术得到了网络的同步判据.但上述工作主要集中在拓扑结构固定不变的网络同步问题，并未涉及变结构离散网络的同步问题.同时，时间混沌系统一直被人们用以研究网络同步的网络节点.相比于时间网络，时空网络因其具有独特的空间特征近年来逐渐被人们采用来研究网络同步问题，但其同步技术依然不够成熟.

值得注意的是，虽然网络同步有滑模控制同步[17-18]、驱动响应同步[19]、自适应同步[20-21]、指数同步[22]和耦合同步[23]等多种类型，但其中的指数同步因在调节网络同步速率方面有其独特的优势，因而受到人们的广泛青睐.为此，文献[24]研究了具有混合时变时滞的神经网络的自适应指数同步问题.Ahmed 等[25]通过构造Lyapunov 函数研究了一类具有有向拓扑和时滞的复杂网络的指数同步问题.文献[26]研究了具有时变内耦合的复杂动态网络的指数同步，并获得了确保网络指数同步的充分条件.但据我们所知，目前关于离散型时空网络的指数同步方案还鲜有报道.

基于上述讨论，本文研究了具有拓扑切换特性的离散型不确定时空网络的指数同步，并对网络中的未知参数进行了识别.这种同步技术的优势在于网络的拓扑结构可按照人为的需要任意切换，其同步性能不受影响.同时，我们构造了一个具有指数形式的特殊的Lyapunov 函数，通过调节其中的参数，能够有效地调节网络的同步速率.

1 时空网络与目标系统的指数同步

考虑N个离散型时空混沌系统作为节点的时空网络与单一目标系统的指数同步.目标系统取如下形式:

其中，n为离散化时间，m为空间格点坐标，F(y(m，n)，α) 是目标系统的状态函数.f(y(m，n))是经过适当分离后得到的不含系统参数的部分，g(y(m，n))α为含有系统参数的部分，α为系统参数.

网络节点的动力学方程取如下形式:

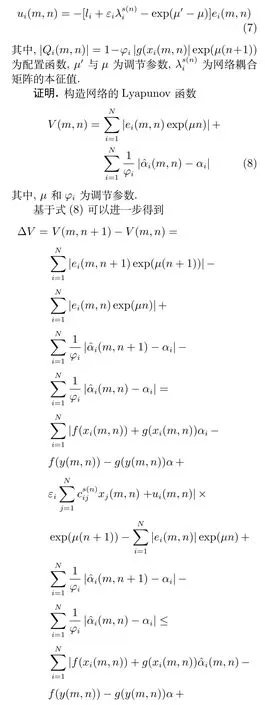
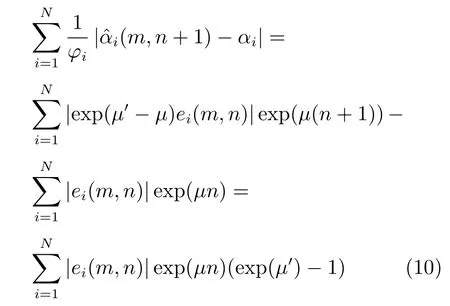
显然，若exp(μ′)-1＜0，即μ′ ＜0，必有ΔV＜0.基于Lyapunov 稳定性理论，上述网络与目标系统达到指数同步.

2 仿真模拟与分析

为了验证同步方案，我们选取具有时空混沌行为的激光相位共轭波空间拓展系统[27-28]作为目标系统和时空网络的节点进行仿真模拟.

激光相位共轭波空间拓展系统的状态方程为

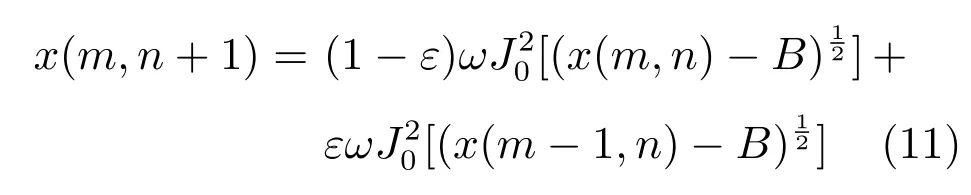
其中，系统参数ω=28，B=1，ε=0.1，而J0表示零级Bessel 函数.

针对上述方程，取周期性边界条件，并且初始值在(1.8，2) 区间内随机取值，我们仿真模拟了激光相位共轭波空间拓展系统状态变量随时空的演化如图1 所示.明显地，该系统处于时空混沌态.

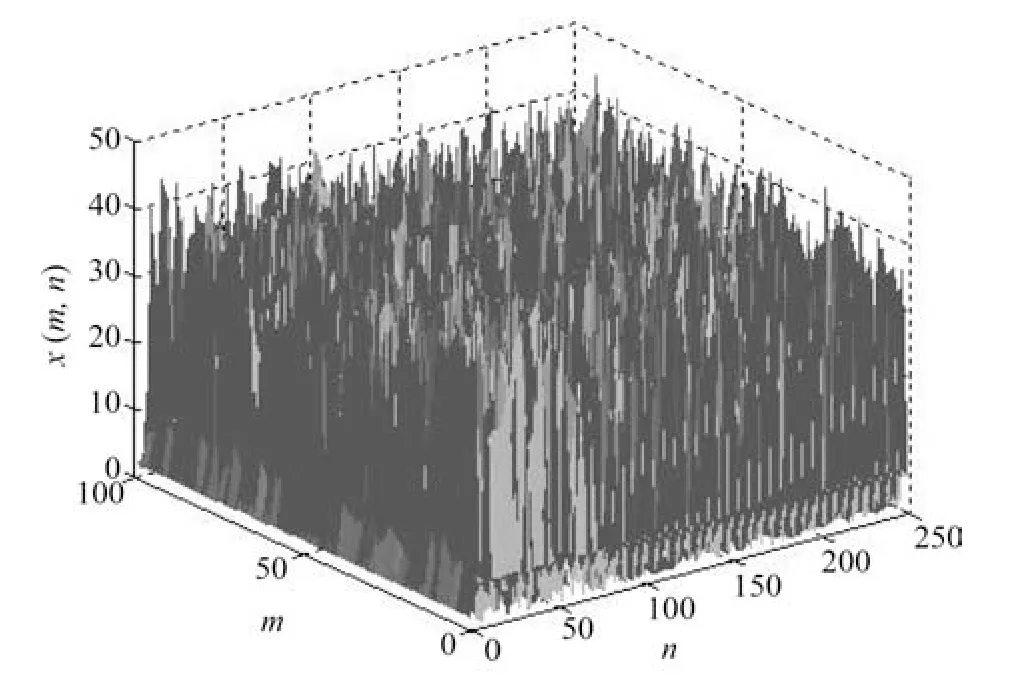
图1 状态变量x(m，n) 的时空演化Fig.1 Spatiotemporal evolution of state variable x(m，n)

在仿真模拟中，目标系统取单一的激光相位共轭波空间拓展系统

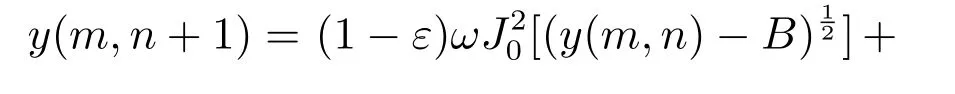
任选网络节点数N=7，基于式(2) 构造网络节点的动力学方程

其中，参数ε在模拟过程中假设为未知量.

选取时间段[0，250]，并假设相应的切换信号s(n) 如图2 所示.我们选取4 种时空网络的拓扑结构与切换信号s(n)对应，如图3 所示.具体来说，例如当时间n=[0，50)时，对应切换信号s(n)=1，即此时的时空网络的拓扑结构为图3(a)，对应的耦合矩阵为C1;当时间n=[50，80) 时，切换信号s(n)=3，即此时的时空网络的拓扑结构为图3(c)，对应的耦合矩阵为C3.显然，不同时间段的切换信号s(n) 都有一一对应的拓扑结构，且与拓扑结构对应的耦合矩阵为

图2 拓扑切换信号s(n)Fig.2 The topology switching signal s(n)

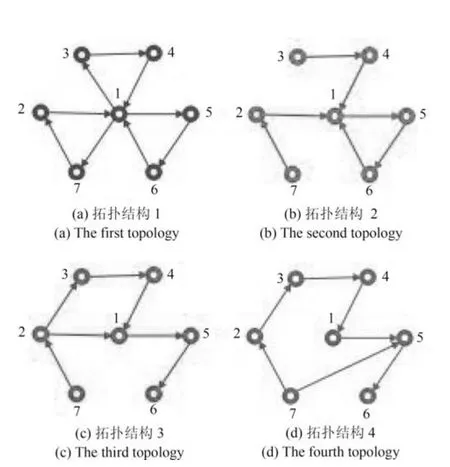
图3 4 种切换拓扑结构图Fig.3 Four switching topologies

基于式(6) 和式(7)，我们可以获得对应的网络控制器及其参数识别律，其中相关参数取为μ′=-0.09，μ=-0.01，φi=0.012.取周期性边界条件，网络节点状态变量的初始值仍随机选取，我们模拟网络误差随时空的演化如图4～10 所示，参数识别量随时空的演化如图11～17 所示.

图4 误差e1(m，n) 随时空的演化Fig.4 Spatiotemporal evolution of error e1(m，n)

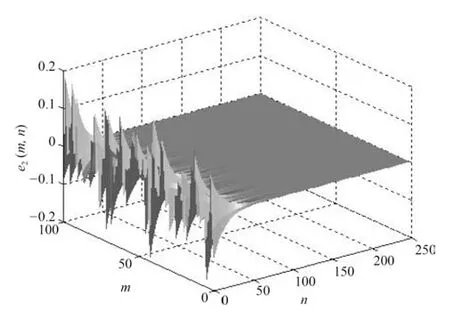
图5 误差e2(m，n) 随时空的演化Fig.5 Spatiotemporal evolution of error e2(m，n)

图6 误差e3(m，n) 随时空的演化Fig.6 Spatiotemporal evolution of error e3(m，n)

图7 误差e4(m，n) 随时空的演化Fig.7 Spatiotemporal evolution of error e4(m，n)

图8 误差e5(m，n) 随时空的演化Fig.8 Spatiotemporal evolution of error e5(m，n)

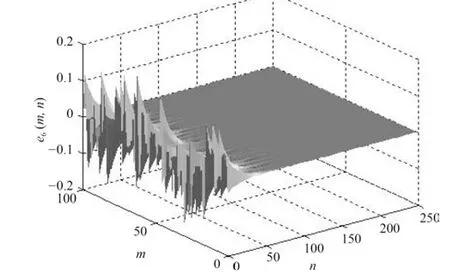
图9 误差e6(m，n) 随时空的演化Fig.9 Spatiotemporal evolution of error e6(m，n)

由图4～10 可以发现网络误差ei(m，n) 在初始阶段存在一定振荡但经过较短时间后振荡明显减弱并且当n=60 时同步误差迅速收敛于零此时网络达到了指数同步状态.同时，保持其他参数不变，调节参数μ取不同的数值，网络的同步误差趋于零的快慢程度是不同的，可见指数同步在控制同步速率方面有较大的优势.另外，从图中也可以看到，在整个时间序列[0，250]上，即使网络拓扑结构随着切换信号任意变化，但网络误差收敛于零后一直保持稳定状态，说明网络拓扑结构的切换并不影响网络的同步性能.图11～17 显示，由于初始值不同，未知参数εi(m，n) 的识别图像在n=60 之前有明显的波动.但在此之后逐渐趋于定值0.1，与参数的实际值一致，表明未知参数的识别效果明显.

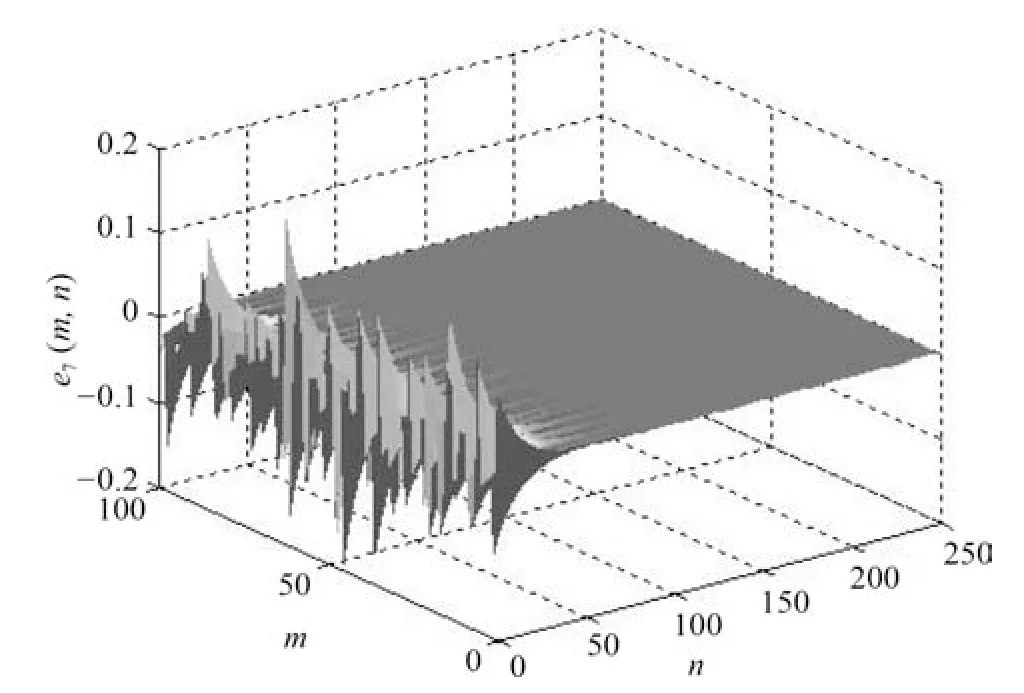
图10 误差e7(m，n) 随时空的演化Fig.10 Spatiotemporal evolution of error e7(m，n)

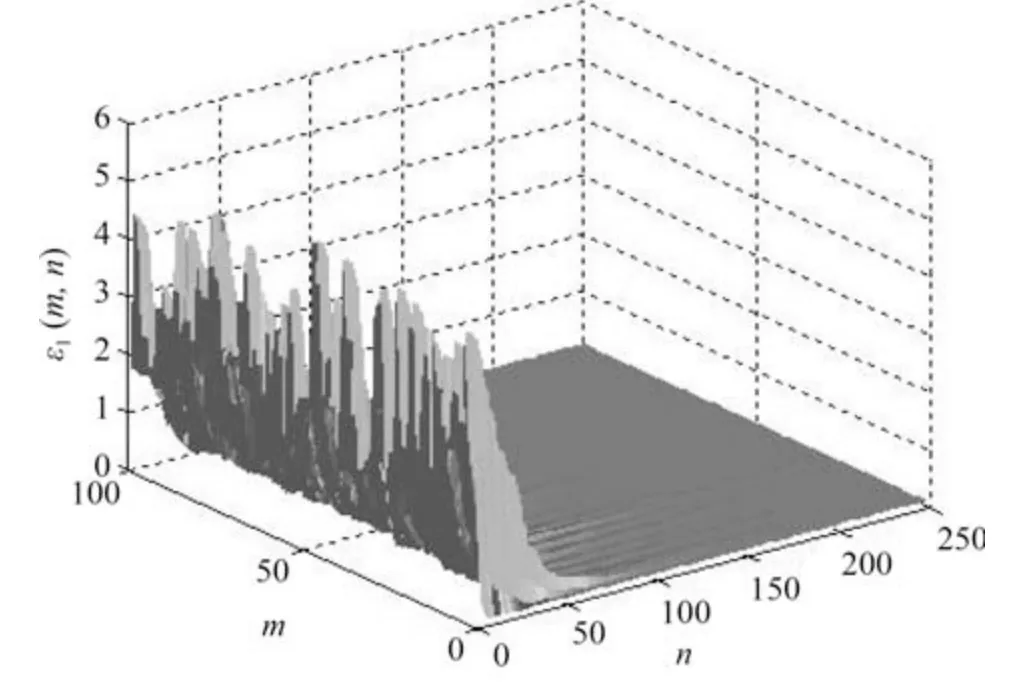
图11 未知参数ε1(m，n) 随时空的演化Fig.11 Spatiotemporal evolution of unknown parameter ε1(m，n)

图12 未知参数ε2(m，n) 随时空的演化Fig.12 Spatiotemporal evolution of unknown parameter ε2(m，n)

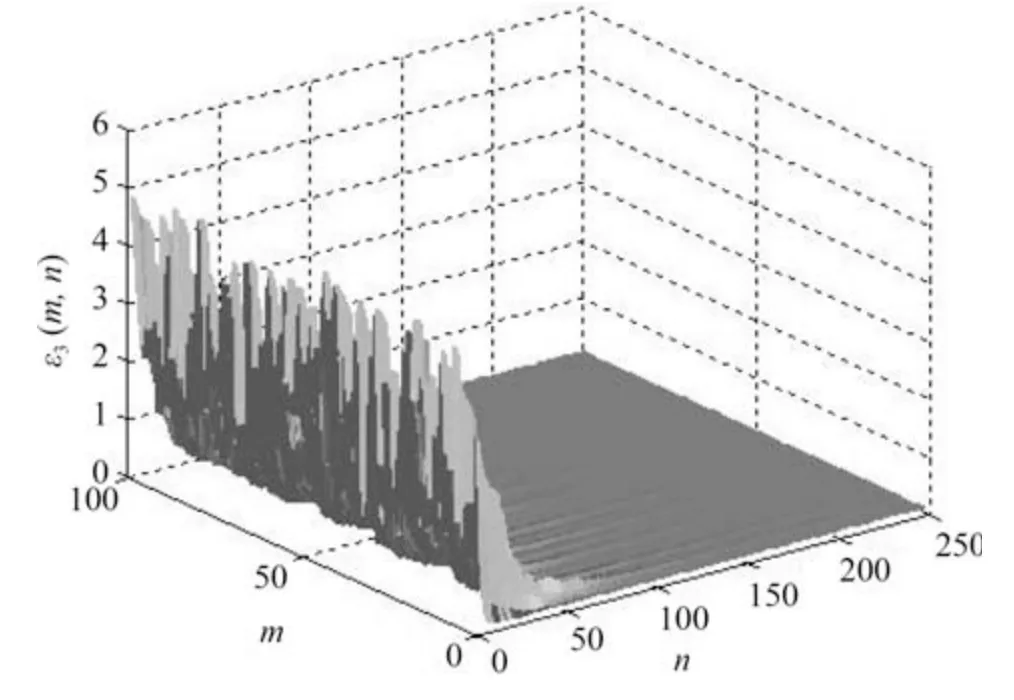
图13 未知参数ε3(m，n) 随时空的演化Fig.13 Spatiotemporal evolution of unknown parameter ε3(m，n)

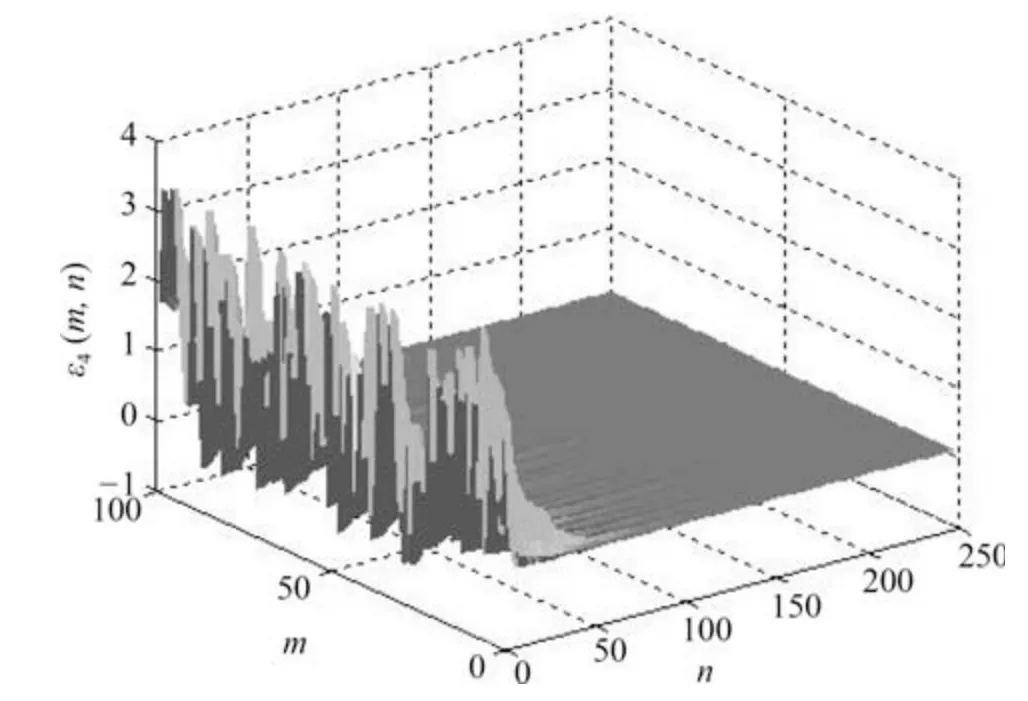
图14 未知参数ε4(m，n) 随时空的演化Fig.14 Spatiotemporal evolution of unknown parameter ε4(m，n)

图15 未知参数ε5(m，n) 随时空的演化Fig.15 Spatiotemporal evolution of unknown parameter ε5(m，n)

图16 未知参数ε6(m，n) 随时空的演化Fig.16 Spatiotemporal evolution of unknown parameter ε6(m，n)

图17 未知参数ε7(m，n) 随时空的演化Fig.17 Spatiotemporal evolution of unknown parameter ε7(m，n)

3 结论

在时空网络的拓扑结构随着切换信号的变换而变化的情况下，通过设计有效的同步控制器和含有指数形式的Lyapunov 函数，我们实现了含有未知参数的离散型时空网络与单一目标的指数同步，并且未知参数也得到了有效的识别.通过仿真模拟，我们进一步验证了设计的同步原理的有效性.模拟结果表明，网络误差ei(m，n) 在较短的时间内趋于零，未知参数的识别曲线经过短时间波动后也趋于定值0.1.我们发现，变化的网络拓扑结构并没有对网络的同步性能产生影响，并且指数同步策略能够有效地控制网络的同步速率.